Matematika»Analisiak
Funtzioen azterketa orokorra
Funtzioak aplikazio asko dituzte zientzia guztietan, eta analisi
matematikoaren helburu nagusi dira. Gehienetan funtzio baten
adierazpen aljebraikoa ezagutzen da, hau da, funtzioa ematen duen
y =f(x) formula; horregatik, adierazpen aljebraiko horretatik abiatuz
funtzioaren ezaugarriak ateratzean jakitea hain garrantzitsua da.
Gai honetan problema hau landuko da, eremua, simetriak, asintotak
eta funtzioaren adierazpenetik zuzenean lortzen diren datu orokorrak,
deribatuaren bidez lortzen diren gorapena eta muturrak
bezalakoekin elkartuz. Datu hauen laburpena funtzioaren grafikoaren
bidez, hau da, (x,f(x)) erako puntu-multzoaren bidez azal daiteke
. Lortzen diren datuak, ez dute funtzioaren ezagutza osoa ematen,
horretarako funtzioko infinitu puntuak jakin beharko liratekeelako,
baina ezaugarririk garrantzitsuenak ematen ditu.Funtzioaren azterketa egiterakoan, puntu garrantzitsuren bat ez
ahazteko, ordena egoki bat jarraitu behar da, nahiz eta askotan,
kontuan hartzeko baliorik ematen ez dutelako, puntu bat baino
gehiago baztertzen den.Orden eroso bat hau izan daiteke :- f-tik zuzenean ateratzen diren tasunak.Izate-eremua eta ibiltarteaSimetriaka) OY ardatzarekiko simetria. Funtzio bikoitia
b) Jatorriarekiko simetria. Funtzio bakoitiaPeriodikotasunaf-ren zeinua. X'X ardatzarekiko ebaki-puntuakBornapenaKonbergentzia edo hurbildura. Asintotak
a) Asintota bertikalak
b) Asintota horizontalac) Asintota zeiharraJarraitasuna.Y'Y ardatzarekiko ebaki-puntuak. Puntu lagungarriakOndoz ondoko deribatuetatik lortutako f-ren propietateak.Monotoniaa) Tarte gorakorrak
b) Tarte beherakorrakMuturrak : Maximo eta minimoakAhurtasuna eta ganbiltasuna
a) Tarte ahurrak
b) Tarte ganbilakInflexio-puntuak
I. Izate-eremua, ibiltartea, simetriak, zeinuak.
Atal honetan funtzioaren formulatik, limiteak eta deribatuak aplikatu gabe ateratzen diren ezaugarriak aztertzen dira.
1. Izate-eremua
f funtzio baten izate-eremua, funtzioa definitua dagoen zenbaki
errealen multzoari esaten zaio.Praktikan, y = f(x) adierazpenaren bidez emandako funtzio baten
izate-eremua ez da zehazten, halakotan, y = f(x) adierazpenak zentzua
duen izate-eremurik handiena bilatu behar da.• Adibideak:1. Bilatu funtzioaren izate-eremua.Frakzio bat denez, izendatzailea anulatzen ez den beste balio
denetan definituta dago.
funtzioaren izate-eremua.Frakzio bat denez, izendatzailea anulatzen ez den beste balio
denetan definituta dago.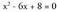 eginez x = 2 edo x = 4 lortzen da. BerazE = R - {2,4}.2. Bilatu
eginez x = 2 edo x = 4 lortzen da. BerazE = R - {2,4}.2. Bilatu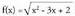 funtzioaren izate-eremua.Erro karratu funtzioa definituta dago errokizuna 0 baino handiagoa edo berdina denean; beraz, kasu honetan f definituta dago
funtzioaren izate-eremua.Erro karratu funtzioa definituta dago errokizuna 0 baino handiagoa edo berdina denean; beraz, kasu honetan f definituta dago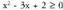 denean, edo gauza bera denez,
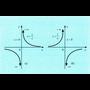
denean, edo gauza bera denez, funtzioa positiboa denean. g funtzioaren grafikoa 1. irudikoa da, eta bertan ikusten denez, R - (1,2) tartetan definituta dago.
funtzioa positiboa denean. g funtzioaren grafikoa 1. irudikoa da, eta bertan ikusten denez, R - (1,2) tartetan definituta dago.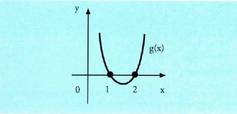 3. Bilatu
3. Bilatu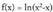 funtzioaren izate-eremua.Logaritmo funtzioa definituta dago, zenbakia 0 baino handiagoa denean ; beraz f definituta egongo da
funtzioaren izate-eremua.Logaritmo funtzioa definituta dago, zenbakia 0 baino handiagoa denean ; beraz f definituta egongo da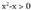
2. Simetria
a) OY ardatzarekiko simetria. Funtzio bikoitiaf funtzioa bat, Y'Y ardatzarekiko simetrikoa dela esaten da, izateeremuko edozein f(-x) = f(x) denean. f funtzioa, funtzio bikoitiadela ere, esaten da.P(x,y) puntu bat f grafikakoa bada, eta f funtzioa Y'Y ardatzarekiko
simetrikoa bada, orduan P'(-x,y) puntua ere grafikakoa da.
Beraz, abzisa negatiboeri dagokion grafika zatia abzisa positiboeri
dagokion grafika zatiaren simetrikoa da Y'Y ardatzarekiko.Adibidea.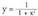 , funtzio bikoiti bat da.
, funtzio bikoiti bat da.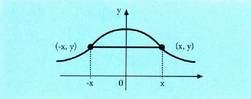 b) 0(0,0) jatorriarekiko simetria. Funtzio bakoitia.f funtzioa bat jatorriarekiko simetrikoa dela esaten da, izate-eremuko
edozein x-entzat f(-x) _ - f(x) denean. f funtzioa, funtzio
bakoitia dela ere esaten da.P(x,y) puntu bat f grafikakoa bada, eta f funtzioa jatorriarekiko
simetrikoa bada, orduan P'(-x,-y) puntua ere grafikakoa da. Beraz
abzisa negatiboei dagokien grafika zatia, abzisa positiboei dagokien
grafika zatiaren simetrikoa da jatorriarekiko.• Adibidea :
b) 0(0,0) jatorriarekiko simetria. Funtzio bakoitia.f funtzioa bat jatorriarekiko simetrikoa dela esaten da, izate-eremuko
edozein x-entzat f(-x) _ - f(x) denean. f funtzioa, funtzio
bakoitia dela ere esaten da.P(x,y) puntu bat f grafikakoa bada, eta f funtzioa jatorriarekiko
simetrikoa bada, orduan P'(-x,-y) puntua ere grafikakoa da. Beraz
abzisa negatiboei dagokien grafika zatia, abzisa positiboei dagokien
grafika zatiaren simetrikoa da jatorriarekiko.• Adibidea :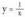 funtzio bikoiti bat da.
funtzio bikoiti bat da.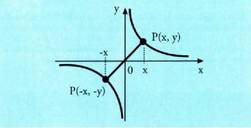 • Adibidea:1.
• Adibidea:1. bada, orduan
bada, orduan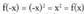 ; beraz, f-ren grafikoa Y'Y ardatzarekiko simetrikoa edo bikoitia da.2.
; beraz, f-ren grafikoa Y'Y ardatzarekiko simetrikoa edo bikoitia da.2.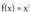 bada, orduan
bada, orduan ; beraz, f-ren grafikoa jatorriarekiko simetrikoa edo bakoitia da.3.
; beraz, f-ren grafikoa jatorriarekiko simetrikoa edo bakoitia da.3. bada, orduan
bada, orduan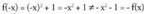 ; beraz, ez da jatorriarekiko simetrikoa.
; beraz, ez da jatorriarekiko simetrikoa.
Baina ez da Y'Y ardatzarekiko simetrikoa ere, izan ere,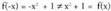
3. Periodikotasuna
f(x) funtzio bat periodikoa da periodoa deritzan eta nulua ez den
T zenbaki erreal bat existitzen bada, izate-eremuko edozein x baliorentzat
f(x + T) = f(x) dela betetzen dena.F funtzio periodiko bat bada, eta T periodo bat, , ere periodo bat da. T periodo duen funtzio periodikoa aipatzen denean, T periodorik txikiena dela ulertzen da. Periodo honi periodo nagusi esaten zaio.(x, x+T) periodo bateko baliotarako funtzio baten grafikoa ezaguna
bada, OX ardatzean traslazio bat eginez atera daiteke funtzio
osoa.
, ere periodo bat da. T periodo duen funtzio periodikoa aipatzen denean, T periodorik txikiena dela ulertzen da. Periodo honi periodo nagusi esaten zaio.(x, x+T) periodo bateko baliotarako funtzio baten grafikoa ezaguna
bada, OX ardatzean traslazio bat eginez atera daiteke funtzio
osoa.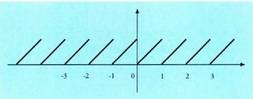 Funtzio Trigonometrikoak funtzio periodikoak dira :
Funtzio Trigonometrikoak funtzio periodikoak dira :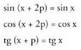 • Adibideak :1.
• Adibideak :1.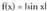 funtzioa, funtzio periodikoa da, eta bere periodoa p da, izan ere,
funtzioa, funtzio periodikoa da, eta bere periodoa p da, izan ere,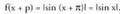
4. f funtzioaren zeinuak. X'X ardatzarekiko ebaki-puntuak
f funtzioak E izate-eremuan hartzen dituen balioen zeinua honako
erlazio hauen araberakoa da :a) f(x) > 0, funtzioa hertsiki positiboa da.b) f(x) = 0, funtzioa nulua da.c) f(x) < 0, funtzioa hertsiki negatiboa da.b)-n lortutako x puntuak, funtzioaren erro edo zeroak dira. Geometrikoki,
funtzioak eta abzisa-ardatzaren arteko ebaki-puntuak
dira.• Adibidea :1. Aztertu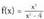 funtzioaren zeinua.f funtzioaren zeinua aztertzeko, zenbakitzailearen eta izendatzailearen
zeinuak, zein bere aldetik hartuko dira, eta gero batera zatidura
bezala hartuko dira.
funtzioaren zeinua.f funtzioaren zeinua aztertzeko, zenbakitzailearen eta izendatzailearen
zeinuak, zein bere aldetik hartuko dira, eta gero batera zatidura
bezala hartuko dira.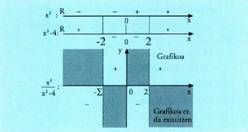
5. Bornatzea eta ibiltartea.
Funtzio bat bornatua dago ibiltartea bornatuta dagoenean. Funtzioa
bornatua badago, honako hau kalkulatu daiteke :a) Goi-muturra. Ibiltartekoa bada, maximoa deitzen zaio.b) Behe-muturra. Ibiltartekoa bada, minimo deitzen zaio.Funtzio bat bornatuta badago, haren grafikoa y = goren(f) eta y =
beheren(f) zuzenek mugatutako tartean dago.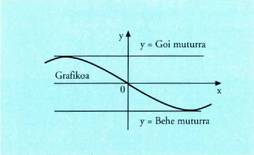 • Adibidea:1. Aztertu f(x) = cos x funtzioaren bornatzeaDakigunez, kosinu funtzioaren baliorik handiena 1 da, eta baliorik
txikiena -1 da ; beraz goi eta behe-bornatua dago.Bere grafikoa y = 1 eta y = -1 zuzenek mugatutako bandan dago.
• Adibidea:1. Aztertu f(x) = cos x funtzioaren bornatzeaDakigunez, kosinu funtzioaren baliorik handiena 1 da, eta baliorik
txikiena -1 da ; beraz goi eta behe-bornatua dago.Bere grafikoa y = 1 eta y = -1 zuzenek mugatutako bandan dago.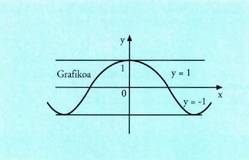 2. Aztertu
2. Aztertu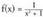 funtzioaren bornatzea.
funtzioaren bornatzea.
Baliorik handiena x = 0 eta f(0) = 1 denean hartzen du.
Funtzioa beti positiboa denez, behe-borne bat y = 0 da.
Behe-muturra zein den ikusiko dugu. Honako hau daukagu : Funtzioaren asintota horizontala y = 0 = beheren(f) zuzena da.
Funtzioaren asintota horizontala y = 0 = beheren(f) zuzena da.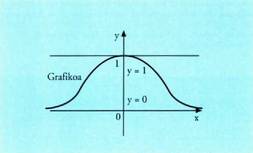 y = f(x) funtzioa emanda, ibiltartea aurkitzeko erarik errazena,
y = f(x) funtzioa emanda, ibiltartea aurkitzeko erarik errazena,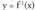 alderantzizko funtzioaren izate-eremua bilatzea da.Adibideak :1.
alderantzizko funtzioaren izate-eremua bilatzea da.Adibideak :1.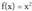 . Alderantzizko funtzioa
. Alderantzizko funtzioa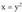 . y bakanduz edo despejatuz :
. y bakanduz edo despejatuz :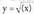 . Funtzio honen izate-eremua, zenbaki erreal positiboek, zeroa barne, osatzen dute. Beraz hori da lehenengo funtzioaren ibiltartea.2.
. Funtzio honen izate-eremua, zenbaki erreal positiboek, zeroa barne, osatzen dute. Beraz hori da lehenengo funtzioaren ibiltartea.2.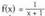 funtzioaren alderantzizko funtzioa
funtzioaren alderantzizko funtzioa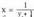 da. y bakanduz, xy + x = 1 denez,
da. y bakanduz, xy + x = 1 denez,
I I. Asintotak. Jarraitasuna.
L'Hopital-en erregela
1. Asintotak
Atal honetan, hasteko, x edo y hautaz oso handiak edo oso txikiak,
hau da oo-rantz jotzen dutenean, zer gertatzen den aztertuko da.Egoera desberdinak, -rantz jotzen duen aldagaiaren arabera sailka daitezke :y-k mugarik gabe gora edo behera jotzen du, hau da
-rantz jotzen duen aldagaiaren arabera sailka daitezke :y-k mugarik gabe gora edo behera jotzen du, hau da -rantz edo
-rantz edo -rantz jotzen du, x aldagaia
-rantz jotzen du, x aldagaia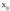 balio finitura hurbiltzen denean.
balio finitura hurbiltzen denean.
Hau gertatzen 9. irudiko x = 1 puntuan. Kasu honetan kurbaren grafikoa zuzen bertikal batera hurbiltzen da, eta funtzioak asintota bertikal bat duela esaten da.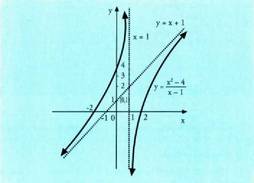 x aldagaiak mugarik gabe gora edo behera jotzen du, y menpeko
aldagaiak k balio finitu baterantz jotzen duen bitartean. Kasu honetan,
grafikoa zuzen horizontal batera hurbiltzen denez, kurbak
asintota horizontal bat duela esaten da. Hau gertatzen da 10. irudian
y = 0 zuzenarekin.
x aldagaiak mugarik gabe gora edo behera jotzen du, y menpeko
aldagaiak k balio finitu baterantz jotzen duen bitartean. Kasu honetan,
grafikoa zuzen horizontal batera hurbiltzen denez, kurbak
asintota horizontal bat duela esaten da. Hau gertatzen da 10. irudian
y = 0 zuzenarekin.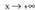 -rantz edo
-rantz edo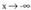 -rantz doanean, y aldagaia ere, hautaz, gora edo behera doanean. Infinitu balio horretara hurbiltzen den eraren arabera egoera desberdinak bereiz daitezke :Kurba zuzen batera hurbiltzen da, orduan, kurbako y aldagaia,
edozein zuzenetan egiten duen baino lasterrago edo geldiroago haz
daiteke,
-rantz doanean, y aldagaia ere, hautaz, gora edo behera doanean. Infinitu balio horretara hurbiltzen den eraren arabera egoera desberdinak bereiz daitezke :Kurba zuzen batera hurbiltzen da, orduan, kurbako y aldagaia,
edozein zuzenetan egiten duen baino lasterrago edo geldiroago haz
daiteke, kasuan bezala zuzen batera hurbiltzen denean, kurbak asintota zeihar bat duela esaten da.
kasuan bezala zuzen batera hurbiltzen denean, kurbak asintota zeihar bat duela esaten da. -rantz zuzen batean baino lasterrago jotzen badu, adar paraboliko bertikal bat duela esaten da. Hau da
-rantz zuzen batean baino lasterrago jotzen badu, adar paraboliko bertikal bat duela esaten da. Hau da edo
edo funtzioetan gertatzen dena.
funtzioetan gertatzen dena. -rantz zuzen batean baino geldiroago jotzen badu, adar paraboliko horizontal bat duela esaten da. Hau da y = ln x edo
-rantz zuzen batean baino geldiroago jotzen badu, adar paraboliko horizontal bat duela esaten da. Hau da y = ln x edo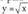 funtzioetan gertatzen dena..
funtzioetan gertatzen dena..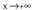 eta
eta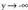 -rantz jotzen dutenean ikusitako hau zailtasunik gabe
-rantz jotzen dutenean ikusitako hau zailtasunik gabe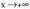
a) Asintota bertikala
Bedi f funtzio bat, bere izate-eremua R-ko E duena.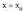 zuzena asintota bertikala dela esaten da, honako hau betetzen denean :
zuzena asintota bertikala dela esaten da, honako hau betetzen denean :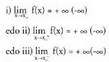 hau da,
hau da, -n asintota bertikala izateko, gutxienez limiteetariko batek existitu behar du eta limite horrek infinitu izan behar du.Funtzio baten asintota bertikalak, i), ii), edo iii) erlazioetariko bat egiaztatzen duen
-n asintota bertikala izateko, gutxienez limiteetariko batek existitu behar du eta limite horrek infinitu izan behar du.Funtzio baten asintota bertikalak, i), ii), edo iii) erlazioetariko bat egiaztatzen duen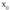 zenbaki errealak zehaztuz lortzen dira.• Adibideak :1. Bilatu
zenbaki errealak zehaztuz lortzen dira.• Adibideak :1. Bilatu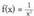 , funtzioaren asintota bertikalak.x= 0 denean
, funtzioaren asintota bertikalak.x= 0 denean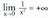 da.
da.
Asintota bertikala x = 0 da.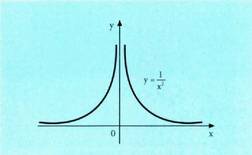 2. Bilatu
2. Bilatu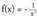 , funtzioaren asintota bertikalak.Funtzio hau aurreko adibidean azaldutako funtzioaren aurkako
funtzioa da. Bere asintota x= 0 izango du, izan ere :
, funtzioaren asintota bertikalak.Funtzio hau aurreko adibidean azaldutako funtzioaren aurkako
funtzioa da. Bere asintota x= 0 izango du, izan ere :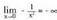 da.Bere grafikoa aurrekoaren OX ardatzerekiko simetrikoa du.3.
da.Bere grafikoa aurrekoaren OX ardatzerekiko simetrikoa du.3.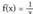 funtzioaren grafikoa hiperbola aldekide bat da. x = 0 zuzena asintota bertikala da.
funtzioaren grafikoa hiperbola aldekide bat da. x = 0 zuzena asintota bertikala da.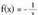 funtzioak ere asintota bera dauka.
funtzioak ere asintota bera dauka.
b) Asintota horizontala
Bedi f funtzio bat, bere izate-eremua R-ko E duena. y = k zuzena
asintota horizontala dela esaten da, honako hau betetzen denean :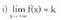 edo
edo Asintota horizontala izateko, gutxienez aurreko limite horietako
batek existitu behar du.• Adibideak:1.
Asintota horizontala izateko, gutxienez aurreko limite horietako
batek existitu behar du.• Adibideak:1.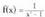 funtzioaren asintota horizontala y = 0 da, izan ere
funtzioaren asintota horizontala y = 0 da, izan ere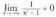 2.
2.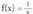 funtzioa eta
funtzioa eta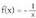
c) Asintota zeiharra
 -rantz, edo
-rantz, edo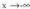 -rantz doanean y = mx + b zuzena y = f(x) kurba baten asintota zeiharra dela esaten da, funtzioaren grafikoaren eta zuzen horren arreko diferentzia gero eta txikiagoa denean, x gero eta handiago edo gero eta txikiago egin ahala. Honen ondorioz, ordenatuen arteko aldea gero eta txikiagoa da.x bakoitzarentzat honako hau daukagu :
-rantz doanean y = mx + b zuzena y = f(x) kurba baten asintota zeiharra dela esaten da, funtzioaren grafikoaren eta zuzen horren arreko diferentzia gero eta txikiagoa denean, x gero eta handiago edo gero eta txikiago egin ahala. Honen ondorioz, ordenatuen arteko aldea gero eta txikiagoa da.x bakoitzarentzat honako hau daukagu :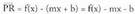 Argi dagoenez,
Argi dagoenez,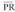 -k zerorantz jotzen duenean asintota eta kurbaren adarra hurbildu egiten dira. Hori kontuan izanik definizio hau eman dezakegu :Bedi f funtzio bat, bere izate-eremua R-ko E duena. y = mx + b,
-k zerorantz jotzen duenean asintota eta kurbaren adarra hurbildu egiten dira. Hori kontuan izanik definizio hau eman dezakegu :Bedi f funtzio bat, bere izate-eremua R-ko E duena. y = mx + b,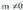 , zuzena f-ren asintota zeiharra dela esaten da, honako hau betetzen denean :
, zuzena f-ren asintota zeiharra dela esaten da, honako hau betetzen denean :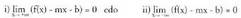 Asintota zeiharra izateko, aurreko limite horietako batek, gutxienez,
existitu behar du.y = mx + b,
Asintota zeiharra izateko, aurreko limite horietako batek, gutxienez,
existitu behar du.y = mx + b,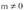 asintota zeiharra zehaztuta geldituko da, m eta b-ren balioak ezagutzen direnean.Ikus dezagun nola kalkulatzen diren x-ek
asintota zeiharra zehaztuta geldituko da, m eta b-ren balioak ezagutzen direnean.Ikus dezagun nola kalkulatzen diren x-ek -rantz jotzen duenean :
-rantz jotzen duenean : 1) m maldaren kalkulua :
1) m maldaren kalkulua :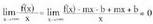 mx + b gehitu eta kendu
mx + b gehitu eta kendu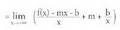 propietate banakorra
propietate banakorra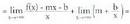 batura baten limitea=mizan ere lim (f(x) - mx - b) = 0 da.Beraz
batura baten limitea=mizan ere lim (f(x) - mx - b) = 0 da.Beraz •
•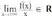 bada, orduan, kurbak asintota zeihar bat dauka.. Kasu honetan m-ek asintotaren norabidea ematen du, eta "norabide asintotikoa" esaten zaio. Kurbaren adarra "hiperbolikoa" dela esaten da.•
bada, orduan, kurbak asintota zeihar bat dauka.. Kasu honetan m-ek asintotaren norabidea ematen du, eta "norabide asintotikoa" esaten zaio. Kurbaren adarra "hiperbolikoa" dela esaten da.•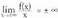 bada, orduan, kurbak asintota zeihar bat dauka, t- , x eta dagokion adarrari, OY norabideko "adar parabolikoa" esaten zaio.•
bada, orduan, kurbak asintota zeihar bat dauka, t- , x eta dagokion adarrari, OY norabideko "adar parabolikoa" esaten zaio.• bada, orduan, kurbak asintota zeihar bat dauka, eta dagokion adarrari, OX norabideko "adar parabolikoa" esaten zaio.Hiru aukera hauek 9. eta 11. iruditan ikus daitezke.2) b jatorri-ordenatuaren kalkuluam ezagutuez gero, b horrela kalkulatzen da :
bada, orduan, kurbak asintota zeihar bat dauka, eta dagokion adarrari, OX norabideko "adar parabolikoa" esaten zaio.Hiru aukera hauek 9. eta 11. iruditan ikus daitezke.2) b jatorri-ordenatuaren kalkuluam ezagutuez gero, b horrela kalkulatzen da :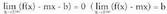 Beraz,
Beraz,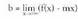 • Adibideak:1. Bila
• Adibideak:1. Bila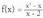 fimtzioaren asintotak.a) Asintota bertikalak : x = 2b) Asintota horizontala : ez daukae) Asintota zeiharra :
fimtzioaren asintotak.a) Asintota bertikalak : x = 2b) Asintota horizontala : ez daukae) Asintota zeiharra :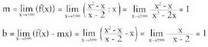 Beraz, asintota zeiharra y = x + 1 da.2. Bila
Beraz, asintota zeiharra y = x + 1 da.2. Bila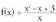 funtzioaren asintotak.Kasu honetan asintota zeiharra metodo orokorra erabiliz kalkula
daiteke, baina praktikan, beste metodo hau oso egokia izaten da :
funtzioaren asintotak.Kasu honetan asintota zeiharra metodo orokorra erabiliz kalkula
daiteke, baina praktikan, beste metodo hau oso egokia izaten da : (zatiketa egitea aski da)Beraz asintota zeiharra y = x - 1 da ; izan ere, x-ek plus edo minus infiniturantz jotzen badu, funtzioa y = x - 1 zuzenera hurbiltzen da,
(zatiketa egitea aski da)Beraz asintota zeiharra y = x - 1 da ; izan ere, x-ek plus edo minus infiniturantz jotzen badu, funtzioa y = x - 1 zuzenera hurbiltzen da,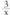
2. L'Hôpital-en erregela
Funtzioak korapilatsuagoak direnean, asintotak kalkulatzeko egin behar diren limiteak ere korapilatu egiten dira. Kasu horretan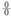 edo
edo edo indeterminazioak ebazteko balio duen L´Hôpital-erregelaerabiltzea komeni da. Zenbakitzaileko eta izendatzaileko adierazpenek,ohiko funtzioetan arazo ez diren jarraitasun eta deribagarritasun
baldintza batzuk bete behar dituzte.
edo indeterminazioak ebazteko balio duen L´Hôpital-erregelaerabiltzea komeni da. Zenbakitzaileko eta izendatzaileko adierazpenek,ohiko funtzioetan arazo ez diren jarraitasun eta deribagarritasun
baldintza batzuk bete behar dituzte.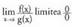 edo
edo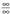 erako indeterminazio bat bada, orduan,
erako indeterminazio bat bada, orduan,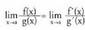 Erregela hau ,
Erregela hau , -rantz edo
-rantz edo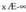 -rantz doan kasurako orokortu daiteke.• Adibideak :
-rantz doan kasurako orokortu daiteke.• Adibideak :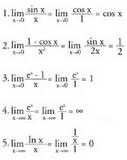 Baina erregela erabiltzen hasi aurretik, indeterminazioa
Baina erregela erabiltzen hasi aurretik, indeterminazioa edo
edo erakoa dela ikusi behar da, izan ere holakoak gerta daitezke :
erakoa dela ikusi behar da, izan ere holakoak gerta daitezke :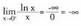 Edo desberdina den beste hau :
Edo desberdina den beste hau :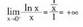 Aplikazioa :Bila
Aplikazioa :Bila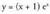 funtzioaren asintotakFuntzio hau R osoan jarraia da, eta ez dauka asintota bertikalik.
funtzioaren asintotakFuntzio hau R osoan jarraia da, eta ez dauka asintota bertikalik.
Asintota horizontalik duen ikusteko hau egingo da :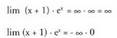 L´Hôpital-ene erregela erabili ahal izateko,
L´Hôpital-ene erregela erabili ahal izateko,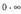 indeterminazioa
indeterminazioa erara pasa behar da :
erara pasa behar da :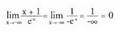 Beraz asintota horizontal bat dauka, eta bere ekuazioa
Beraz asintota horizontal bat dauka, eta bere ekuazioa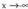 -rantz doanean y = 0 da, eta
-rantz doanean y = 0 da, eta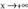
3. Jarraitasuna
Gogora dezagun : f funtzioa,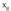 puntuan jarraia da hau betetzen denean :
puntuan jarraia da hau betetzen denean :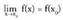
4. Y'Y ardatzekiko ebaki-puntuak. Puntu lagungarriak
Izan bedi y = f(x) funtzio bat. f funtzioaren grafikoak eta OY
ardatzaren arteko ebaki-puntuak, honako sistema hau ebatziz lortzen
dira: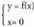 Beraz, ebaki-puntuak (0,f(0)) erakoak dira.
Beraz, ebaki-puntuak (0,f(0)) erakoak dira.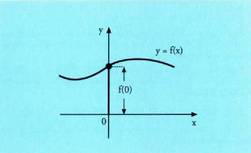
I I I. Ondoz ondoko deribatuetatik lortutako f-ren propietateak.
Monotonia, maximo eta minimoak, ahurtasuna eta ganbiltasuna eta inflexio puntuen azterketa deribagarria den edo ez den edozein funtziotan egin daiteke. Funtzioa deribagarria denean , propietate hauen azterketa sakona aurreko gaian egin da. Zorionez, oinarrizko maila honetan erabiltzen ditugun ia funtzioa denak, puntu bakan batzutan ezik, beste denetan, deribagarriak dira.Deribatuekin landu behar diren puntuak, laburbilduz, hauek dira :
f '(x) lehenengo deribatuarekin :
- Tarte gorakor/beherakorrak. -entzat, f '(x) > 0 bada, y = f(x) funtzioa (a,b) tartean gorakorra da.
-entzat, f '(x) > 0 bada, y = f(x) funtzioa (a,b) tartean gorakorra da.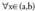 -entzat, f '(x) < 0 bada, y = f(x) funtzioa (a,b) tartean beherakorra da.
-entzat, f '(x) < 0 bada, y = f(x) funtzioa (a,b) tartean beherakorra da.
- Mutur erlatiboak : f(x) funtzioa, - ren ingurune batean deribagarria bada, eta
- ren ingurune batean deribagarria bada, eta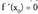 bada.
bada.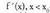 -entzako positibo izatetik,
-entzako positibo izatetik,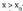 -entzako negatibo izatera aldatzen bada, funtzioak maximo erlatibo bat dauka
-entzako negatibo izatera aldatzen bada, funtzioak maximo erlatibo bat dauka puntuan.
puntuan.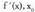 puntuan negatibo izatetik positibo izatera pasatzen bada, funtzioak minimo erlatibo bat dauka
puntuan negatibo izatetik positibo izatera pasatzen bada, funtzioak minimo erlatibo bat dauka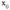 puntuan.f '(x) funtzioaren zeinua,
puntuan.f '(x) funtzioaren zeinua,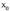 puntuan aldatzen ez bada, funtzioak inflexio-puntu bat dauka
puntuan aldatzen ez bada, funtzioak inflexio-puntu bat dauka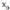
f "(x) bigarren deribatuarekin:
- Ahurtasuna eta ganbiltasuna :
-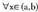 -entzat, f "(x) > 0 bada, y = f(x) funtzioa 0 (a,b) tartean ahurra da. Beraz, f'(x o ) = 0 eta f "(x) > 0 badira, funtzioak,
-entzat, f "(x) > 0 bada, y = f(x) funtzioa 0 (a,b) tartean ahurra da. Beraz, f'(x o ) = 0 eta f "(x) > 0 badira, funtzioak,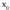 puntuan, minimo erlatibo bat dauka.
puntuan, minimo erlatibo bat dauka.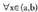 -entzat, f"(x) < 0 bada, y = f(x) funtzioa (a,b) tartean ganbila da. Beraz,
-entzat, f"(x) < 0 bada, y = f(x) funtzioa (a,b) tartean ganbila da. Beraz,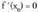 eta f "(x) < 0 badira, funtzioak,
eta f "(x) < 0 badira, funtzioak, puntuan, maximo erlatibo bat dauka.
puntuan, maximo erlatibo bat dauka.
- Inflexio-puntua : f "(x o ) = 0 bada eta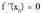 bada eta
bada eta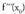 edo beste edozein deribatu bakoitiren balio
edo beste edozein deribatu bakoitiren balio puntuan zero ez bada, y = f(x) funtzioak,
puntuan zero ez bada, y = f(x) funtzioak,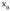 puntuan, inflexio puntu bat dauka.• Adibideak :1. Azter ezazu
puntuan, inflexio puntu bat dauka.• Adibideak :1. Azter ezazu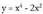 funtzioa.- f-ren izate-eremua : E = R- Simetria : f bikoitia da,
funtzioa.- f-ren izate-eremua : E = R- Simetria : f bikoitia da,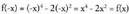 delako.- Asintotak eta adarrak :
delako.- Asintotak eta adarrak :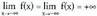 - Ardatzekiko ebaki-puntuak :x = 0 ; f(0) = 0
- Ardatzekiko ebaki-puntuak :x = 0 ; f(0) = 0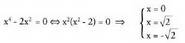 - Tarte gorakor/beherakorrak
- Tarte gorakor/beherakorrak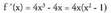 inserted text
inserted text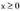 denean bakarrik egingo da.
denean bakarrik egingo da.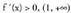 tartean denez, f funtzioa
tartean denez, f funtzioa tartean hertsiki gorakorra da.f ' (x) < 0, (0,1) tartean denez, f funtzioa [0,1 ] tartean hertsiki
beherakorra da.- Maximo eta minimo erlatiboak
tartean hertsiki gorakorra da.f ' (x) < 0, (0,1) tartean denez, f funtzioa [0,1 ] tartean hertsiki
beherakorra da.- Maximo eta minimo erlatiboak ; funtzioak maximo bat dauka x = 0 puntuan
; funtzioak maximo bat dauka x = 0 puntuan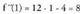 ; funtzioak minimo bat dauka x = 1 puntuan.- Tarte ahur/ganbilak
; funtzioak minimo bat dauka x = 1 puntuan.- Tarte ahur/ganbilak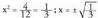 f"(x)<0 da
f"(x)<0 da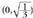 tartean, beraz, f funtzioa ganbila da
tartean, beraz, f funtzioa ganbila da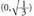 tartean.. ´´ (x) > 0 da
tartean.. ´´ (x) > 0 da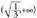 tartean, beraz, f funtzioa ahurra da
tartean, beraz, f funtzioa ahurra da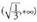
- Inflexio-puntuak
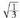 puntuan, funtzioak inflexio-puntu bat dauka, puntu horretan funtzioa, ganbila izatetik ahurra izatera pasatzen delako.
puntuan, funtzioak inflexio-puntu bat dauka, puntu horretan funtzioa, ganbila izatetik ahurra izatera pasatzen delako.
- Taula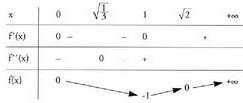 Funtzio honi dagokion grafikoa hau da.
Funtzio honi dagokion grafikoa hau da.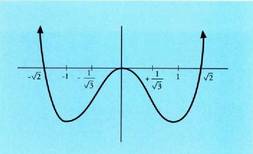 2. Irudika ezazu
2. Irudika ezazu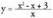 funtzioa.
funtzioa.
Funtzio hau horrela idatzi daiteke : - f-ren izate-eremua : E = R* = R - {0}- Simetria: ez dauka.- Asintotak hauek dira : x = 0 eta y = x - 1- Funtzioa izate-eremu osoan jarraia da.-
- f-ren izate-eremua : E = R* = R - {0}- Simetria: ez dauka.- Asintotak hauek dira : x = 0 eta y = x - 1- Funtzioa izate-eremu osoan jarraia da.-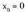 puntuan alboetako limiteak hauek dira :
puntuan alboetako limiteak hauek dira : - Ardatzekiko ebaki-puntuak :Ardatzak ez ditu ebakitzen ; izan ere, x > 0 denean y > 0 da, eta x
< 0 denean, y < 0 da.- Tarte gorakor/beherakorrak eta maximo/minimoak :Lehenengo deribatua y'= 1 -X da.
- Ardatzekiko ebaki-puntuak :Ardatzak ez ditu ebakitzen ; izan ere, x > 0 denean y > 0 da, eta x
< 0 denean, y < 0 da.- Tarte gorakor/beherakorrak eta maximo/minimoak :Lehenengo deribatua y'= 1 -X da.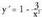 da.
da.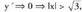 , beraz f gorakorra da
, beraz f gorakorra da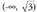 eta
eta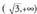 tartetan.
tartetan. edo
edo beraz f funtzioak maximo bat dauka
beraz f funtzioak maximo bat dauka puntuan, eta minimo bat dauka
puntuan, eta minimo bat dauka puntuan, gero bigarren deribatua lantzerakoan ikusi daiteken bezala.
puntuan, gero bigarren deribatua lantzerakoan ikusi daiteken bezala.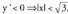 , beraz f beherakorra da
, beraz f beherakorra da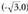 eta
eta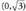 tartetan.- Tarte ahur/ganbilak eta inflexio-puntuak :Bigarren deribatua :
tartetan.- Tarte ahur/ganbilak eta inflexio-puntuak :Bigarren deribatua : da y " > 0 (x > 0, beraz f ahurra da R , -ny "= 0 ez du soluziorik, beraz ez dauka inflexio punturik.y " < 0 (x < 0, beraz f ganbila da R-n-Taula
da y " > 0 (x > 0, beraz f ahurra da R , -ny "= 0 ez du soluziorik, beraz ez dauka inflexio punturik.y " < 0 (x < 0, beraz f ganbila da R-n-Taula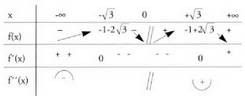 Funtzio honi dagokion grafikoa hau da.
Funtzio honi dagokion grafikoa hau da.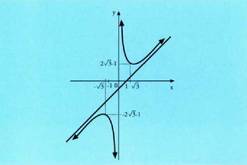 3. Azter ezazu
3. Azter ezazu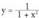 funtzioa- Izate-eremua : E = R- Simetria :
funtzioa- Izate-eremua : E = R- Simetria :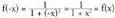 beraz f bikoitia da.- Asintotak : Horizontala
beraz f bikoitia da.- Asintotak : Horizontala -rantz eta
-rantz eta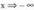 -rantz doanean.- Ardatzekiko ebaki-puntuak :OY ardatza (0,1) puntuan ebakitzen duOX ardatza ez du ebakitzen, izan ere
-rantz doanean.- Ardatzekiko ebaki-puntuak :OY ardatza (0,1) puntuan ebakitzen duOX ardatza ez du ebakitzen, izan ere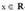 -entzat f(x) > 0 da.- Tarte gorakor/beherakorrak
-entzat f(x) > 0 da.- Tarte gorakor/beherakorrak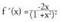 f '(x) > 0, x < 0 denean denez, f funtzioa
f '(x) > 0, x < 0 denean denez, f funtzioa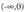 tartean gorakorraf '(x)< 0, x > 0 denean denez, f funtzioa
tartean gorakorraf '(x)< 0, x > 0 denean denez, f funtzioa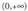 tartean beherakorra da.- Maximo eta minimo erlatiboak(0,1) puntua maximo erlatiboa da- Tarte ahur/ganbilak
tartean beherakorra da.- Maximo eta minimo erlatiboak(0,1) puntua maximo erlatiboa da- Tarte ahur/ganbilak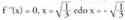 denean izango da.f --aren zeinua
denean izango da.f --aren zeinua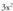 funtzioarena izango da, beraz :
f´´(x) > 0 da
funtzioarena izango da, beraz :
f´´(x) > 0 da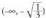 eta
eta tarteetan, beraz, f funtzioa,tarte horietan, ahurra da.. "(x) < 0 da
tarteetan, beraz, f funtzioa,tarte horietan, ahurra da.. "(x) < 0 da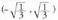 tartean, beraz, f funtzioa, tarte horretan, ganbila da.- Inflexio-puntuak :
tartean, beraz, f funtzioa, tarte horretan, ganbila da.- Inflexio-puntuak : eta
eta puntuetan ahurtasuna/ganbiltasuna aldatzen denez, 3 puntu horiek inflexio-puntuak dira.- Taula
puntuetan ahurtasuna/ganbiltasuna aldatzen denez, 3 puntu horiek inflexio-puntuak dira.- Taula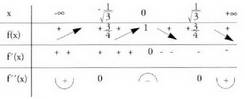 Funtzio honi dagokion grafikoa hau da :
Funtzio honi dagokion grafikoa hau da :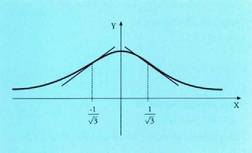 4. Azter ezazu f(x) = x - sin x funtzioa- Izate-eremua: Zenbaki erreal guztiak- Simetria : f(-x) = - f(x). Funtzio hau bakoitia da.- Asintotak : Ez dauka asintotarik, nahiz eta
4. Azter ezazu f(x) = x - sin x funtzioa- Izate-eremua: Zenbaki erreal guztiak- Simetria : f(-x) = - f(x). Funtzio hau bakoitia da.- Asintotak : Ez dauka asintotarik, nahiz eta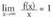 izan, baina gero
izan, baina gero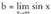 kalkulatzerakoan, limitea indeterminatuadeia ateratzen da.- Ardatzekiko ebaki-puntuak : P(O,O)- Periodikotasuna
kalkulatzerakoan, limitea indeterminatuadeia ateratzen da.- Ardatzekiko ebaki-puntuak : P(O,O)- Periodikotasuna dela egiaztatu arren, funtzio hau ez da periodikoa.- Tarte gorakor/beherakorrak
dela egiaztatu arren, funtzio hau ez da periodikoa.- Tarte gorakor/beherakorrak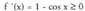 da ; beraz beti gorakorra da eta ez dauka ez maximo ez minimo erlatiborik.- Bigarren deribatua : f "(x) = sin x da, eta
da ; beraz beti gorakorra da eta ez dauka ez maximo ez minimo erlatiborik.- Bigarren deribatua : f "(x) = sin x da, eta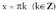 denean, anulatu egiten da,
denean, anulatu egiten da, puntu horiek inflexio-puntuak dira, izan ere balio horietan
puntu horiek inflexio-puntuak dira, izan ere balio horietan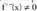 da.- Taula
da.- Taula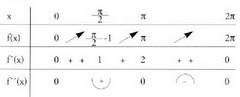 Funtzio honi dagokion grafikoa hau da :
Funtzio honi dagokion grafikoa hau da :
IV Ezagunak diren funtzio batzuetatik abiatuz, beste funtzio batzuk irudikatzeko era
Askotan, funtzio batzuk, ezagunak diren beste funtzio batzuk erabiliz eraiki daitezke, baina bi funtzio horiek, funtzioen arteko eragiketen bidez elkarrekin erlazionaturik egon behar dute.Besteren artean hiru kasu hauek aipatuko dira :1. Aurkako funtzioak2. Alderantzizko funtzioak3. Balio absolutu funtzioak
1. Aurkako funtzioak
Aurkako diren bi funtzio, OX ardatzarekiko simetrikoak dira.
Bietariko bat ezagutuz gero, bestea, simetriaren bidez eraikitzen da.• Adibidea:1. Irudika itzazu eta g(x) _ - sin x funtzioak.
eta g(x) _ - sin x funtzioak.
Bi funtzio hauek,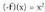 eta (-g)(x) = sin x funtzioen aurkakoak dira. Beraz, hauen grafikoak, -f eta -g Funtzioak ezagutzen
direnez, 20 irudikoak dira.
eta (-g)(x) = sin x funtzioen aurkakoak dira. Beraz, hauen grafikoak, -f eta -g Funtzioak ezagutzen
direnez, 20 irudikoak dira.
2. Alderantzizko funtzioak
Alderantzizko diren bi funtzio, lehenengo eta hirugarren koadranteko
erdikariarekiko simetrikoak dira. Bietariko bat ezagutuz
gero, bestea, simetriaren bidez eraikitzen da.• Adibidea:1. Irudika itzazu bi funtzio hauek :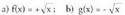 Bi funtzio hauek R -etan definitutako
Bi funtzio hauek R -etan definitutako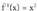 eta R-tan definitutako
eta R-tan definitutako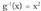 funtzioen alderantzizko funtzioak dira. Beraz,
funtzioen alderantzizko funtzioak dira. Beraz, eta
eta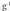 grafikoak ezagutuz, eskatutakoak 21. Irudiko (a) eta (b) dira :
grafikoak ezagutuz, eskatutakoak 21. Irudiko (a) eta (b) dira :
3. Balio absolutu funtzioa
f funtzioa ezagutuz, Ifl funtzioa eraiki behar da. Horretarako, f
eraiki ondoren, f-ren zati negatiboa, OX ardatzarekiko simetriaren
bidez irudikatuko da.• Adibidea:1. Irudika itzazu funtzio hauek : Bi funtzio hauek, y = x - 1 eta y = sin x funtzioen balio absolutu
funtzioak dira. Beraz, f eta g funtzioen grafikoak ezagutuz, eskatutakoak
22. irudiko (a) eta (b) dira :
Bi funtzio hauek, y = x - 1 eta y = sin x funtzioen balio absolutu
funtzioak dira. Beraz, f eta g funtzioen grafikoak ezagutuz, eskatutakoak
22. irudiko (a) eta (b) dira :
- Ariketak
1. Azter eta irudika ezazu funtzioa.
funtzioa.
2. Azter eta irudika ezazu funtzioa.
funtzioa.
3. Azter eta irudika ezazu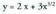 funtzioa.4. Azter eta irudika ezazu
funtzioa.4. Azter eta irudika ezazu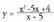
Ebazpide edo soluzioak :
1. 2.
2.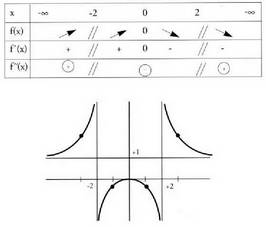 3.
3.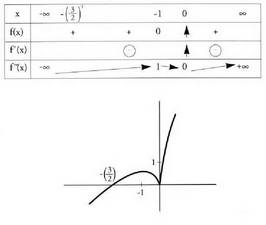 4.
4.