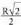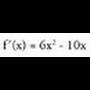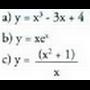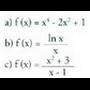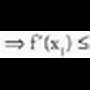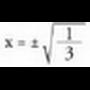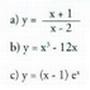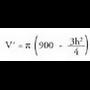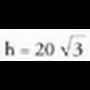Matematika»Analisiak

Deribatua funtzioen azterketan aplikatua

Funtzio baten definizio eremua jakitea (non dagoen definitua eta non ez) ez da, pixka-pixka bat aztertuz gero behintzat, gauza zaila.

Eta horrek gero, ardatz sistema cartesiar baten bidez adierazten baita funtzioa, hura definitua dagoen abzisa ardatzaren puntuetan behartuko gaitu arreta jartzera.Parisko Unibertsitateko irakasle zen Nicole Oresme (1323- 1382) matematikaria izan zen nonbait, bi lerro elkarzuten bidez higidura uniformeki azeleratuaren grafikoa lehenengo egin zuena.

Hala ere, berretzailetzat zatikiak dituzten berreketak (eta berreketen arteko eragiketak) definitzea izan zen Oresmek matematikari egin zion ekarpen handiena.Funtzio baten adierazpen grafikoak funtzioaren definizio hutsak baino informazio gehiago dakar, ikusgai jartzen baitu nola aldatzen den aldagai mendekoa, y, aldagai askeari, x, dagokionez; alegia, argi erakusten duelako noiz den funtzioa gorakorra eta noiz beherakorra, noiz iristen duen punturik gorena eta noiz beherena.Kurba hitzak esanahi bat baino gehiago izanik ere, ardatz sistema cartesiar batean egiten den funtzio baten adierazpen grafiko gisa uler bedi aurrerantzean, alegia, (x, f(x)) erako puntuen adierazpen gisa ulertu bedi aurrerantzean. Puntu multzo hori amaigabea izan ohi denez, ezingo dira banan-banan puntu guztiak grafikoan adierazi, eta hurbiltze batekin konformatu beharko. Kurbaren jokabideaz zenbat eta informazioa gehiago izan, hainbat hobea izango da hurbiltze hori. Hori dela eta, dituen agerbide guztiak bereiztea eta aztertzea komeni da.

I. Funtzio gorakorra eta beherakorra tarte batean

• Funtzio bat gorakorra da [a,b] tartean baldin eta tarte horretako bi puntu harturik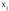etaadibidez, eta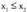izanik,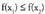dela betetzen bada.Eta hertsiki gorakorra da baldin etaizanik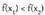dela ondorioztatzen bada.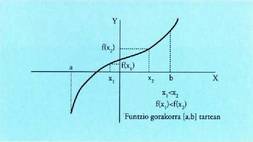inserted textetaadibidez, etaizanik,dela betetzen bada.Eta hertsiki beherakorra izango da baldin etaizanikdela ondorioztatzen bada.

I I. Funtzio gorakorra eta beherakorra puntu batean

• Funtzio bat gorakorra da a puntuan baldin eta tarte ireki bat bada,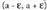, nonbaita, eta hau betetzen bada :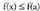izatea baldin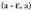tartearen barne bada x, eta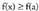izatea baldin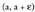tartearen barne bada x.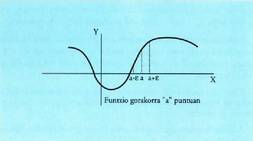• Era berean, ntzio bat beherakorra da a puntuan baldin eta bada tarte ireki bat,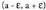, zeinean betetzen baita.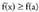izatea, baldin eta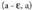barnekoa bada x, eta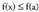izatea, baldin eta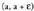barnekoa bada x.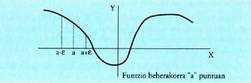Puntu batean hertsiki gorakorra edo beherakorra den funtzioaren definizioa lortzeko aski daordez < jartzea, etaordez, berriz, > jartzea.Argi bereizi behar da, beraz, tarte batean gorakorra edo beherarkorra den funtzioa puntu batean gorakorra edo beherakorra denetik .• AdibideaAztertu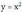funtzioaren goratzea eta beheratzea puntu hauetan :-1 eta 0.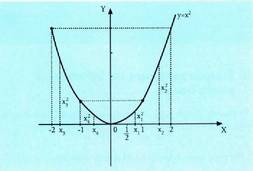Ebazpenafuntzioa hertsiki gorakorra da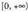tartean, zeren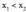baldin bada,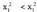. 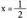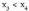Hertsiki gorakorra dapuntuan.Bestalde, hertsiki beherakorra datartean, zeren (zenbaki negatiboak izaki) tarte horretan, baldinbada,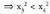(esate baterako, -7 < -3 eta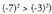

I I I. Funtzio bateko maximoak eta minimoak

f(x) funtzio bat izanik, baldin bada tarte bat,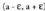, eta f (x) < f (a) bada tarte horretako edozein punturentzat, funtzioak abzisako a puntuan maximo erlatiboa duela esaten da. Kurbako (a, f(a)) puntua izango da, beraz, maximoa.Ordea, baldin f(x) funtzioaren (b - d, b+ d) tartean f(x) > f(a) bada tarte horren barneko edozein puntutan, orduan, f(x) funtzioak b puntuan minimo erlatiboa duela esaten da. Funtzioak, beraz, kur- bako (b, f(b)) puntuan izango du minimoa.Funtzio bateko maximoei eta minimoei, biei mutur erlatibo, edota, besterik gabe, mutur esaten zaie.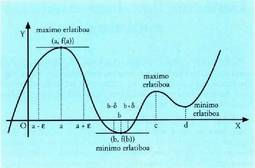Funtzio batek maximo bat baino gehiago eta minimo bat baino gehiago izan ditzake, grafikoan argi eta garbi ikusten denez.Ondorioak1. Kurba baten muturretako bateko ukitzailea abzisa ardatzari buruz paralelo da, eta delako ardatz horrekin zero graduko angelua eratzen du.Hortaz, ukitzaile horiek zero graduko malda dute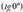, eta nola maldak bat datozen funtzioaren deribatuekin dagozkien abzisa puntuetan, zuzenean ateratzen da ondorioa,etadirela baldin eta a eta b puntuetan maximorik edo minimorik bada.2. Aurrekotik ondorio gisa ateratatzen denez,berdintza betearazten duten balioen artean bilatu behar dira funtzio baten mutur erlatiboak.

Hala ere, artean ez da metodorik jakiteko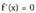ekuazioren ebazpenak maximoak diren, minimoak diren, edo ez maximoak ez minimoak diren.

Esandako guztiak zentzua izango luke baldin eta funtzioa deribagarria balitz bere mutur erlatiboetan, baina, hori, jakina denez, eta irudian argi ikusten denez, ez da beti hala gertatzen.

Hala beraz, (a,f(a)) puntuan badago minimo erlatibo bat, baina funtzioa ez da a puntuan deribagarria; beraz, ez da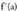-rik.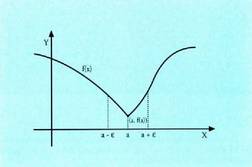Adibidea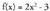funtzioko zer puntuk izan dezake mutur erlatiborik?Ebazpena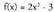funtzioak izan ditzakeen mutur erlatiboak lortzeko hurrengo ekuazio hau ebatzi behar da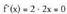

I V. Goratzea, muturrak, eta deribatuaren zeinua

1. Baldin funtzio batek deribatu positiboa badu a puntuan, delako funtzio hori hertsiki gorakorra da puntu horretan.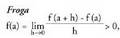, aski h txiki batentzat.Baldin h > 0, f (a + h) f (a) > 0 nahitaez, edo, beste era batera esanda, f (a + h) > f (a).Baldin h < 0, orduan f (a + h) - f (a) < 0, eta, beraz, f (a + h) < f (a).

Hala beraz, horrek frogatzen duen bezala, funtzioa gorakorra da a puntuan.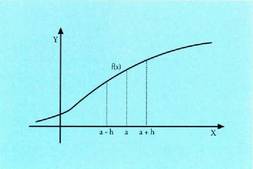2. Baldin f (x) funtzioak deribatu negatiboa badu a puntuan, funtzioa hertsiki beherakorra da puntu horretan.FrogaAurreko puntuan bezalakoa.h txikia bada,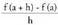zatidura negatiboa da, eta, beraz.f(a + h) - f(a) < 0 baldin h > 0 bada - f(a + h) < f(a) baldin h > 0 bada, etaf(a + h) - f(a) > 0 baldin h < 0 bada ---> f(a + h) > f(a) baldin h < 0 bada.Hala beraz, horrek guztiak frogatzen duen bezala, f(x) funtzioa hertsiki beherakorra da a puntuan.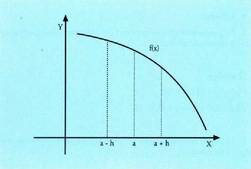• Adibidea1. Aztertu funtzio hau,, eta esan gorakorra alabeherakorra den 1 eta 2 puntuetan.Ebazpena f(x) deribatu :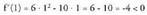Funtzioa hertsiki beherakorra da x = 1 puntuan.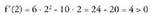Funtzioa hertsiki gorakorra da x = 2 puntuan.3. Baldin funtzio batek maximo edo minimo erlatibo bat badu a puntuan etabada, orduan,izango da nahi eta nahi ez.Froga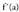positiboa balitz, funtzioa hertsiki gorakorra izango litzateke a puntuan, baina a-n mutur bat baitago, ezinezkoa da hori.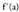negatiboa balitz, funtzioa hertsiki beherakorra izango litzateke a puntuan, baina a-n mutur bat baitago, ezinezkoa da hori.Hala beraz,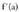, izatekotan,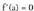izango da nahi eta nahi ez.Beraz, argi geratu den bezala,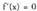ekuazioa ebazten duten balioen artean bilatu behar dira funtzio baten muturrak. Nolanahi ere, gerta daiteke funtzio batek baliorik gabeko deribatua izatea puntu batean eta mutur erlatiborik ez izatea delako puntu horretan, datorren adibideak argi erakusten duen bezala.• Adibidea1. Zer puntutan baliogabetzen da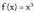funtzioaren deribatua? Mutur erlatiboak al dira?Ebazpena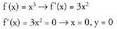(0,0) puntuan ez dago mutur erlatiborik, ondoko grafikoan argi ikusten den bezala.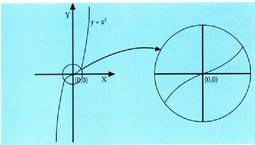4. Baldin f(x) funtzio jarraitua bada [a,b] tarte itxian eta deribagarria (a,b) tarte irekian, deribatua zero delarik [a,b] tarteko puntu guztietan, orduan funtzioa konstantea da.Hau froga zehaztzat hartu ezin badaiteke ere, kontuan izan bedi ezen, deribatua zero baldin bada puntu guztietan, orduan, kurbako puntu bakoitzean, ukitzailea paralelo dela X ardatzari buruz, eta horrek esan nahi duela funtzioaren grafikoa zuzen bat dela, abzisa ardatzaren paralelo. Funtzioa, beraz, f (x) = C = cte.Funtzio deribagarriez egin berri dugun azterketa honetan ondorio gisa ateratzen denez, baldin f (x) deribagarria bada (a, f(a)) puntuan eta puntu horretan mutur erlatiborik bada, orduan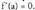Ordea elkarrekikoa ez da zuzena, c irudian ikus daitekeen bezala :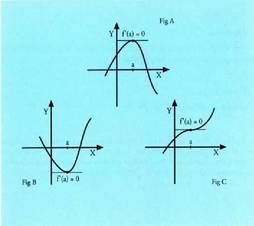Guztietan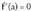

- Ariketak

1. Aurkitu zer tartetan diren gorakorrak edo beherakorrak funtzio hauek :

1. Deribatua izan ditzakeen muturren ezkerrean eta eskuinean aztertzea

Galdera horiei erantzuteko deribatuak a puntuaren ezkerrean eta eskuinean zer zeinu duen aztertu behar da.Kontuan hartu kurbaren ukitzaileek malda negatiboa dutela minimoaren ezkerrean eta positiboa, berriz, eskuinean.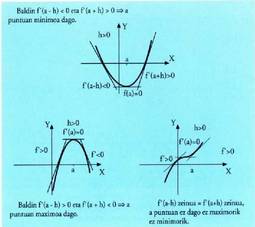• Adibidea1. Zehaztu honako funtzio honen muturrak :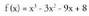Ebazpena• Kalkulatu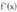f'(x), eta zerorekin berdindu :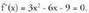Ebatzi ekuazioa :eta• Aztertu deribatuaren zeinua -1 eta 3 puntuen ezkerrean eta eskuinean.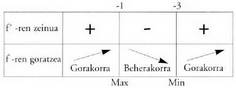x = -1 puntuan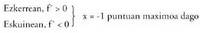x = 3 puntuan2. Zehaztu funtzioaren muturra, eta adierazi maximoa ala minimoa den.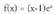Ebazpena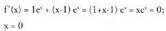Deribatuaren zeinua aztertu behar da 0 puntuaren ezkerrean eta eskuinean.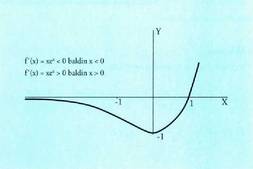2. 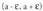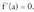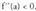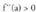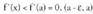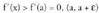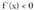Bigarren deribatuaBedi f (x) funtzio deribagarri bat a-ren ingurune batean,etaa) Baldin, funtzioak minimo bat du a puntuan.b) Baldin, funtzioak maximo bat du a puntuan.Frogaa) Nolabaita, f(x) funtzioa hertsiki gorakorra da a puntuan (funtzio deribagarrien lehenengo tasuna)Definizioz,tartean dagoen edozein punturentzat, etatartean dago edozein punturentzat.tarteanbada (eta funtzio deribagarrien bigarren tasunaren bidez ondorioztatzen denez), f(x) funtzioa hertsiki beherakorra da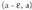tarteko puntuetako bakoitzean, hots, hertsiki beherakorra da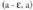tartean. Eta, beraz,f(x) > f(a) da (a - e, a) tarteko edozein punturentzatEra berean eta arrazoi beragatik,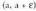tartean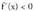bada, delako tarte horretan f(x) hertsiki gorakorra dela ondorioztatzen da.

Hala beraz, f (x) > f (a) da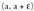tarteko edozein punturentzat.

Baldin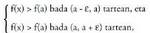Orduan f(x) > f(a) izango da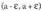tarteko edozein punturentzat eta horrek a puntuan minimo erlatibo bat dagoela esan nahi du.b) Honen frogabidea a) kasurena bezalakoa da.• Adibidea Azertu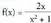funtzioaren muturrak, eta maximoak ala minimoak diren adierazi.Ebazpenaf(x) definitu, eta zerorekin berdindu.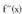kalkulatu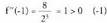puntuan, beraz, minimoa dago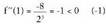

- Ariketak

2. Zehaztu funtzio hauen mutur erlatiboak

V. Ganbiltasuna eta ahurtasuna

Definizioa 1

f(x) funtzioa (a,b) tartean ganbila dela esaten da baldin eta tarte horren barneko edozein punturentzat marrazturiko zuzen ukitzaileak delako funtzio horren grafikoaren gainean geratzen badira.

Definizioa 2

f(x) funtzioa (a,b) tartean ahurra dela esaten da baldin eta tarte horren barneko edozein punturentzat marrazturiko zuzen ukitzaileak delako funtzio horren grafikoaren azpian geratzen badira.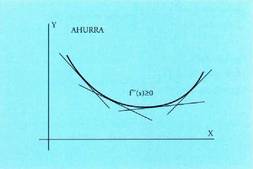Bedi f(x) bi aldiz deribagarri (a,b) tartean.• Lehenengo grafikoan ikus daitekeen bezala, funtzioa ganbila denean, x handitu ahala kurbaren ukitzaileen malda txikiagoa da. Hau da: baldin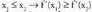. Hala beraz, funtzio deribatua,beherakorra izango da.Gainera, baldin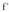beherakorra bada (a,b) barneko puntu batean, edozeinetan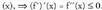f ganbila izango da (a,b) tartean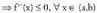Gainera, baldin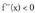bada,ganbila izango da (a,b) tartean.• Funtzioa ahurra denean, x handitzean kurbaren ukitzaileen maldak handituz doaz. 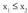Hau da : baldinbada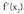. Beraz,gorakorra da eta haren deribatua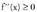f ahurra da (a,b) tartean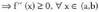Gainera, baldin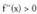bada

VI. Inflexio puntuak

• f(x) funtzioaren grafikoak abzisaren a puntuan inflexio puntua duela esaten da baldin eta (a, f(a)) puntuan kurba ahur izatetik ganbil izatera (edo alderantziz) aldatzen bada, eta ukitzaileak kurba gainetik igarotzen badu, alde bat kurbaren gainean eta bestea azpian duela.

Nola aurkitzen dira inflexio puntuak?

Nola funtzioa ahurra baita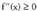denean, eta ganbila, berriz,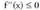denean, eta nola inflexio puntuak ahurtasuna eta ganbiltasuna bereizten baititu, delako puntu horren bigarren deribatua, baldin eta bigarren deribaturik badu, baliogabea izango da nahi eta nahi ez. Beraz, baldin a puntuan inflexio punturik badago,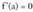izango da.Nolanahi ere, puntu batzuek, inflexio punturik izan gabe ere, zero dute bigarren deribatua.Inflexio punturik izango bada, ahur izatetik ganbil izatera, edo ganbil izatetik ahur izatera, igaro behar du kurbak.Bigarren deribatua duen funtzio bateko inflexio puntuak aurki tzekotan...1. Ebatzi2.bada, aztertu-ren zeinua-ren ezkerrean eta eskuinean. Baldin zeinua aldatzen bada, inflexio puntua da, eta aldatzen ez bada, ez da.Aski deribatu segida onartzen duen funtzio ororentzat froga daitekeen bezala...Baldin f(a) = 0 eta f' (a) = 0 badira eta lehenengo deribatu ez nulua f "(a) bada, orduan, "n" bakoitia bada, funtzioak maximo edo minimo bat izango du a puntuan, eta, aitzitik, "n" bikoitia bada, inflexio puntua izango du.etabadira eta lehenengo deribatu ez nuluabada, orduan, "n" bakoitia bada, funtzioak maximo edo minimo bat izango du a puntuan, eta, aitzitik, "n" bikoitia bada, inflexio puntua izango du.

Baldin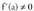eta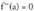badira eta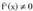funtzioaren lehenengo deribatua bakoitia bada inflexio bat izango da.Baldin eta zero ez den lehenengo deribatua bakoitia bada bigarrenaren ondoren, puntu arrunta izango litzateke orduan, kurba eta ukitzailea beste puntu batzuetan baino elkarrengandik hurbilago dituen puntu arrunt bat.• AdibideaAurkitu ahurtasun eta ganbiltasun tarteak eta inflexio puntua funtzio honetan :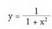Beraz,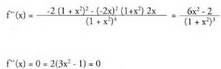Eta hortik, beraz,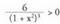izango da beti.Beraz,Beraz,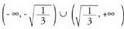tartean f(x) ahurra da, eta,tartean, berriz, ganbila.

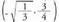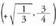Bestalde,puntuan ahur izatetik ganbil izatera igarotzen da kurba, etapuntuan, berriz, ganbiletik ahurrera.Hala beraz,etapuntuak inflexiopuntuak dira.

- Ariketak

3. Aztertu funtzio hauen ahurtasuna eta ganbiltasuna, eta adierazi inflexio puntuak, baldin badituzte :

VII. Optimizazio problemak

Funtzioak x-en zer baliotarako lortzen duen balio maximoa edo minimoa aurkitzea da optimizazio problemen helburua. Hau da, funtzio baten maximo edo minimo absolutua bilatzean dautza.Funtzioa kotagabea baldin bada problemak ez du ebazpenik.

Baina aplikazio gehienetan [a, b] tartean aurkitzen dira x-en balioak, eta, beraz, alde batera utz daitezke adar parabolikoak. Hau da problemaren azalpena :Bedi funtzio bat, y = f(x), [a,b] tartean definitua. Aurkitu, bada, funtzioaren muturrak eta maximo edo minimo absolutuak :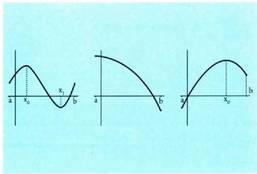Baldin f(x) funtzioa deribagarria bada [a,b] tartean, maximo edo minimo erlatibo bat izan daiteke muturra, edo tartearen muturretako bat, bestela. Beraz,a) Ebatzi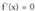funtzioa (a, b] tartean (bitezebazpenak).b) Kalkulatu f(b) eta f(a)c) Alderatu elkarrekin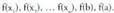. Horietan handiena maximoa da, eta txikiena, berriz, minimoa.

-y = f(x) funtzioa ez da deribagarria zenbait puntutan. Bitez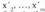puntuak ; puntu horiek, deribaturik ez eta,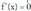funtziotik ezin atera daitezkeen mutur erlatiboak izan daitezke. Elkarrekin alderatu behar dira muturrekin lortzen dena eta deribatuafuntzioekin baliogatzen den puntuak.Baldin funtzioak jauzi-etenak baditu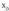-ren batean lim f(x) eta lim f(x) bilatu behar dira eta aurrekoekin alderatu.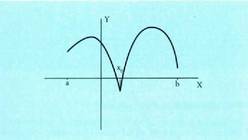EbazpenaPraktian beste problema bat dago lehenago, alegia, fisikan, ekonomian, geometrian edo dena delako zientzian planteatzen den problema tarte jakin batean definituriko funtzio bihurtzea.• Adibidea1. Deskonposatu 32 zenbakia bi batugai positibotan, batugaien biderkadurak maximoa izan behar duela kontuan harturik.Azalpena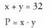P-k maximoa behar du, eta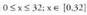Ebazpena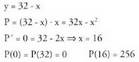Beraz, 16 + 16 batugaietan deskonposatzea da erantzuna2. Erradioa 30 duen esfera bat izanik, aurkitu hartan txerta daitekeen zilindro handienaren bolumena.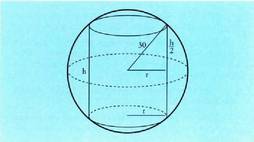AzalpenaZilindro baten bolumena haren oinarriaren arearen eta garaieraren arteko biderkadura da :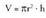r = zilindroaren oinarriaren erradioa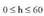Pitagorasen teoremaren arabera.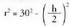Beraz, V-k maximoa behar du.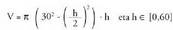Deribatu :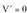mutur baldintza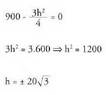Balio negatiboa tarteaz kanpo geratzen da h = 0 eta V = 0 direnean eta h = 60 eta V = 0 direnean.

Baldin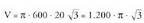eta hori da balio maximoa ; h = 0 eta h = 60 minimoei dagozkie.3. Zilindro itxurako ontzi bat egin nahi da ahalik eta burdinzuri gutxien erabiliz. Ontziak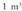-ko bolumena izan behar du. Zer neurri edo luze-zabalera izango du?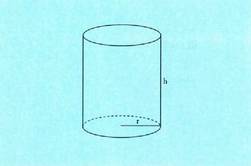AzalpenaNahi den eremurik txikiena :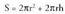Zilindro baten bolumena :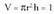r-k eta h-k positiboak izan behar dute.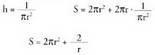Deribatu, eta...Baldin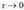edoeremuak infiniturantz joko du.Edo beste era batera esanda :

- Ariketak

4. 5 cm-ko erradioko zirkunferentzia batean txerta daitezkeen laukizuzen guztietatik zein da eremu handiena duena?5. Orri batean-ko testua idatzi nahi bada, eta orrian 1 cm-ko tartea utzi nahi bada albo banatan eta 2 cmkoa goialdean eta behealdean, zenbateko luze-zabalera izan beharko du testuak?6. R erradioko zirkuluerdi batean txerta daitezkeen laukizuzenen artean, aurkitu eremu handiena duena?7. Zer neurri izan behar du laukizuzen batek bere perimetroa ahalik eta txikiena izan dadin, baldin eta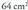

Ebazpenak

l.a) Gorakorra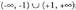; beherakorra (-1, +1).b) Beherakorra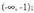; gorakorra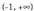c) Gorakorra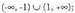; beherakorra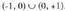2.a) (-1, 0) eta (1, 0) minimo erlatiboak ; (0, 1) maximoa.b) (e, 1 /e) maximoa.c) (-1, -2) maximoa ; (3, 6) minimoa.3.a)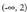ganbila ;ahurra ; ez du inflexio-punturik.b)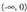ganbila;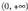ahurra ; (0,0) inflexio-puntua.c)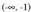ganbila ;ahurra; (-1, -2/e) inflexio-puntua.4. Aldea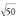duen laukia.5. Orriaren neurriak :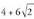bider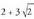6. Diametroaren arabera,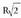luzera eta