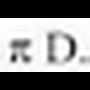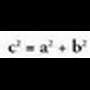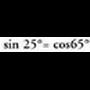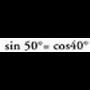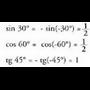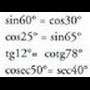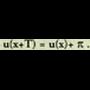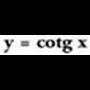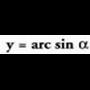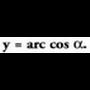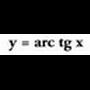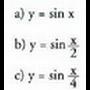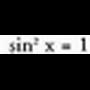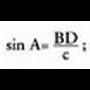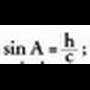Matematika»Trigonometria
Trigonometria
Sarrera
I. Trigonometria
rigonometria, (grekerako trigonometria hitzetik dator, trigonon
triangelua eta metron neurria) triangeluaren elementu batzuek
ezagututa, alde, angelu, altura, etab., ezezagunak diren beste batzuek
kalkulatzeko bideak ematen dituen matematika-adarra da.
Adibidez, bi alde eta angelu baten balioak ezagutu daitezkeenean,
beste aldearen eta bi angeluen balioak jakitera iritsi daiteke. Zehatzago
esanda, trigonometriak triangeluak ebazteko oinarriak ematen
ditu, triangelu lauak izan ala triangelu esferikoak izan.Trigonometriaren ezagutza hau, jakintzaren zuzia zibilizazioz
zibilizazio pasatzen joan ziren jakintsu askori esker metatu ahal
izan da ; horietako batzuek ondoren aipatzen dira.
Pitagoras, bere teorema ezagunarekin. "Triangelu zuzenean,
hipotenusaren karratua, katetuen karratuen baturaren berdina da."Aristarko Samoskoak, Kristo baino hiru mende lehenago,
Ilargiaren eta Eguzkiaren tamaina kalkulatzea erabaki zuen eta
baita Lurretik zein distantzietara zeuden jakitea ere. Horretarako,
honetan oinarritu zen, Ilargia zehatz-mehatz erdi-argituta dagoen
unean, Lurra, Ilargia eta Eguzkia, irudiak azaltzen duen bezalako
triangelu angeluzuzenaren erpinetan daude.
Gaur egun ontzat ematen ditugun emaitzak lortu ez bazituen,
huts hori ezin zaio metodoari bota, metodoa berez zuzena baitzen,
angeluak neurtzeko erabili zituen tresnei baizik, ez baitzuten horretarako
behar zen doitasunik.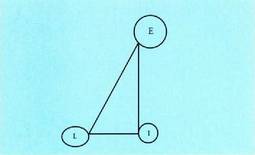
II. Trigonometria laua
Trigonometria lauaren helburua, planoko triangeluak ebaztea da.
Triangelu horiek, zuzenak edota bestelakoak izan daitezke.Triangelu zuzenetan, lau arazo-mota aurki daitezke :
• Hipotenusa eta katetu bat ezagunak izatea.
• Katetu bat eta angelu bat ezagunak izatea.
• Hipotesuna eta angelu bat ezagunak izatea.
• Bi katetuak ezagunak izatea.
Zuzenak ez diren triangeluen kasuan ere, lau arazo-mota agertzen
dira :
• Alde bat eta bi angelu ezagunak izatea.
• Bi alde eta beren arteko angelua ezagunak izatea.
• Bi alde eta horietako baten pareko angelua ezagunak izatea.
• Triangeluaren hiru aldeak ezagunak izatea.
Aipatutako arazo horiek ebazteko, ezinbestekoak dira ondoren
azalduko diren oinarrizko ezagutza eta erlazio batzuek.
III. Oinarrizko ezagutzak
III.1. Angelua.-
Angelua, sorburu berbera duten bi zuzenerdiren artean kokatutako zuzenerdi-multzo gisa har daiteke. Angelua mugatzen duten bi zuzenerdiei alde deritze eta jatorriari berriz erpin.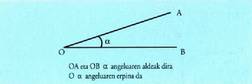 Ondoren datorrenarentzat, komeni da mota honetako angeluak
bereiztea :
• Angelu zuzena, bere aldeak bi zuzenerdi elkartzut direnean.
Ondoren datorrenarentzat, komeni da mota honetako angeluak
bereiztea :
• Angelu zuzena, bere aldeak bi zuzenerdi elkartzut direnean.
• Angelu zorrotza, angelu zuzena baino txikiagoa denean.
• Angelu kamutsa, angelu zuzena baino handiagoa denean.
• Angelu laua, bere aldeak erpinez aurkakoak diren bi zuzenerdi
direnean. Bi angelu zuzenen balioa du.
• Angelu osagarriak, hurrenez hurreneko bi angelu dira eta
bien artean angelu zuzena osatzen dute.
• Angelu betegarriak, hurrenez hurreneko bi angelu dira eta
bien artean bi angelu zuzen osatzen dituzte.
III.2. Angelu orientatua.-
Angelua orientatzea zera da, bera mugatzen duten bi zuzenerdiak ordenatzea da. Batari jatorrizko zuzenerdia deritzo eta besteari muturreko zuzenerdia.
III.3. Noranzko positiboak eta negatiboak angeluentzat.-
Segmentu bat ardatz batekiko orienta daitekeen era berean, angelua ere orienta daiteke. OB jatorrizko aldetzat hartzen bada eta OA muturrekotzat, angelua, trigonometrian POSITIBO (+) dela esaten den noranzkoan marrazten da, izan ere, noranzko hori, ERLOJU-ORRATZEN BIRAKETA-NORANZKOAREN AUR- KAKO NORANZKOA BAITA. Baina alderantziz, OA balitz jatorrizko aldea eta OB muturrekoa, angeluaren noranzkoa, NEGA- TIBOA (-) izango litzateke, erloju-orratzen biraketa-noranzko berbera jarraitu duelako.
III.4. Zirkunferentzia.-
Zirkunferentzia, lerro kurbo itxia da eta bere puntu guztiek, plano berean kokatu eta "zentro" deritzon barruko beste puntu batekiko distantzikide dira, hau da, hartatik distantzia berdinera daude.Zentrotik zirkunferentziaren edozein puntutara dagoen distantziaripuntu elkartzen dituen lerro zuzenari berriz, diametro (D).Diametroak bi erradioren balioa du.
Zirkunferentziaren luzera,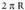 da edota balio bera duen
da edota balio bera duen
III.5. Zirkunferentzia orientatua.-
Zirkunferentzian biraketanoranzko bat aukeratzen denean, zirkunferentzia hori orientatua dagoela esaten da. Noranzkoetako bat positibotzat hartzen da eta bestea negatibotzat. 111.3 puntuan ikusi den legez, trigonometrian noranzko POSITIBOA (+), BIRAKETA ERLOJU ORRATZEN BIRAKETA-NORANZKOAREN AURKAKO NORANZKOAN egiten denean izaten da.
III.6. Arkua.-
Arkua, bi puntuk mugatutako zirkunferentzi zatia da.
III.7. Arku orientatua.-
Arkua orientatzea, mugatzen duten bi puntuak ordenatzea da. Lehenengo puntuari jatorri deritzo eta bigarrenari mutur. Arkuen ibilbidea, noranzko positiboan edota negatiboan egin daiteke.
III.8. Angelu zentrala.-
Erpina zirkunferentziaren zentroan kokatua duen angelua da.
III.9. Koordenatu-ardatzak.-
Elkar perpendikular ebakitzen duten bi lerro zuzen dira. Elkar ebakitzen duten O puntuari koordenatu-jatorri deritzo.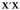 lerro zuzenari abzisa-ardatz deritzo eta
lerro zuzenari abzisa-ardatz deritzo eta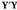 lerro zuzenari ordenatu-ardatz.
lerro zuzenari ordenatu-ardatz.
Planoko edozein P punturentzat, ordenatu-ardatzetik punturainoko distantziari abzisa deitzen zaio eta "x" letraz adierazten da.
Bestalde, abzisa-ardatzetik punturainoko distantziari ordenatu deitzen zaio eta "y" letraz adierazten da. Puntu bakoitzaren abzisa eta ordenatuak osatzen duten multzoari (x,y), koordenatu cartesiar deitzen zaio. Koordenatu horiek, positiboak ala negatiboak izan daitezke. Puntu baten abzisa positiboa dela esango da ordenatu-ardatzaren eskuinaldean badago, eta negatiboa dela, haren ezkerraldean badago. Ordenatua positiboa dela esango da puntua abzisa-ardatzaren gainean badago, eta negatiboa dela, haren azpian badago. Hobeto ulertzeko, ikus irudia.
III.10. Zirkulu-laurdenak (koadranteak).-
Koordenatuardatzek, lau zati berdinetan zatitzen dute planoa eta horietako bakoitzari zirkulu-laurden edo koadrante deitzen zaie : lehen zirkulu-laurdena (koadrantea), bigarren zirkulu-laurdena (koadrantea), hirugarren zirkulu-laurdena (koadrantea) eta laugarren zirkulu-laurdena (koadrantea).
IV. Zirkunferentzia trigonometrikoa edo goniometrikoa
Zirkunferentzia trigonometrikoa edo goniometrikoa, erradioak bat balio duela, jatorritzat abzisa-ardatza hartu eta ibilbidenoranzkoa aukeratua dituen zirkunferentziari deitzen zaio. Noranzko hori, lehen ikusi den bezala, positiboa da erloju-orratzen biraketa-noranzkoaren aurkakoa denean.
V. Angeluak neurtzeko unitateak
V 1.
Angelu zuzena laurogeita hamar zati berdinetan zatituz gero, horietako zati bat, gradu hirurogeitarra da eta
V 2.
Gradu ehundarrak. Gradu ehundarra,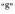 ikurra duena, angelu zuzena ehun zati berdinetan zatitzetik sortzen da.
ikurra duena, angelu zuzena ehun zati berdinetan zatitzetik sortzen da.
Gradu ehundar bakoitza, ehun minututan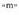 zatitzen da eta minutu bakoitza ehun segundotan
zatitzen da eta minutu bakoitza ehun segundotan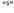 .
.
Unitate hau oso gutxi erabiltzen da, baina badu abantaila : angeluaren balioa,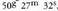 , era hamartarrean idatz daitekeela
, era hamartarrean idatz daitekeela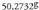
V.3.
Radiana. Radiana, bere arkua erradioaren berdina duen angelu zentrala da eta angeluen neurketan legezko unitatetzat hartzen da. rad ikurrez adierazten da.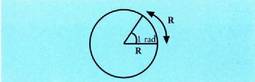 Definizioaren arabera, bere luzera erradioaren berdina duen arku bati radian bateko angelua badagokio, bere luzera
Definizioaren arabera, bere luzera erradioaren berdina duen arku bati radian bateko angelua badagokio, bere luzera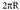 duen zirkunferentziari,
duen zirkunferentziari,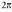 radianeko angelua dagokio.
radianeko angelua dagokio.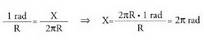 Baldin eta Q bada angelu zentral baten balioa radianetan adierazia
eta "L' berriz R erradioa duen zirkunferentzia batean berari
dagokion arkuaren luzera, arkuaren luzera hori proportzio baten
bidez adieraz daiteke :
Baldin eta Q bada angelu zentral baten balioa radianetan adierazia
eta "L' berriz R erradioa duen zirkunferentzia batean berari
dagokion arkuaren luzera, arkuaren luzera hori proportzio baten
bidez adieraz daiteke :
VI. Radianen eta graduen arteko baliokidetasun-erlazioa.
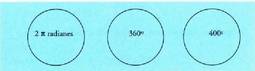 Irudian ikusten denez, zirkunferentzia batek
Irudian ikusten denez, zirkunferentzia batek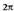 radian edo 360º edo
radian edo 360º edo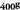 ditu, beraz, baliokidetasuna berehalakoa da :
ditu, beraz, baliokidetasuna berehalakoa da : edota
edota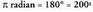 Ebatzitako ariketak.
Ebatzitako ariketak.
1. Bihurtu radianetara ondoko kopuru hauek : 2. Bihurtu gradu hirurogeitarretara ondoko kopuru hauek :
2. Bihurtu gradu hirurogeitarretara ondoko kopuru hauek :
- Proposatzen diren ariketak
1. Bihurtu radianetara ondoko kopuru hauek :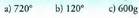 2. Bihurtu gradu hirurogeitarretara ondoko kopuru hauek.
2. Bihurtu gradu hirurogeitarretara ondoko kopuru hauek.
VII. Antzeko triangeluak.
Bi triangeluren hurrenez hurreneko angeluak berdinak badira, bi
triangeluak antzekoak dira eta beren hurrenez hurreneko aldeak
proportzionalak. Bi antzeko triangeluren antzekotasun-arrazoia, beren hurrenez
hurreneko aldeak elkarrekin zatituta ateratzen den "k" zatidura
konstantea da. Arrazoi edo erlazio horri batzuetan "eskala" deitzen
zaio.
Bi antzeko triangeluren antzekotasun-arrazoia, beren hurrenez
hurreneko aldeak elkarrekin zatituta ateratzen den "k" zatidura
konstantea da. Arrazoi edo erlazio horri batzuetan "eskala" deitzen
zaio.
Irudiaren kasuan, k = a b, edo c, izan daiteke.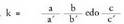
VIII. Triangelu zuzenak. Pitagorasen teorema.
Triangelu angeluzuzena, angelu bat zuzena duena da. Beste bi
angeluak, zorrotzak eta elkarren osagarriak dira. Triangelu zuzenetan
bakarrik aplika daiteke Pitagorasen teorema ; honela dio :
"Triangelu angeluzuzenean, hipotenusaren karratua, katetuen
karratuen baturaren berdina da."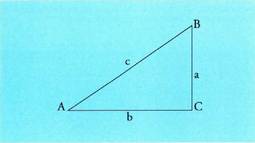 Triangelu honetan :
Triangelu honetan :
IX. Triangelu angeluzuzeneko aldeen eta angeluen arteko erlazioak.
Triangelu angeluzuzenaren aldeen eta angeluen arteko arrazoiei
edo erlazioei, arrazoi trigonometrikoak deitzen zaie. Sei arrazoi
daude, hiru zuzenekoak: sinua, kosinua eta tangentea; eta bestehiru aurrekoen alderantzizkoak : kosekantea, sekantea eta
kotangentea.Aurreko puntuko triangeluaren laguntzaz definituko dira.Sinua (sin). Angelu zorrotzaren sinua (sin), bere pareko katetuaren
eta hipotenusaren arteko arrazoia (zatidura) da.Kosinua (cos). Angelu zorrotzaren kosinua (cos), bere alboko
katetuaren eta hipotenusaren arteko arrazoia (zatidura) da.Tangentea (tg). Angelu zorrotzaren tangentea (tg), bere pareko
katetuaren eta albokoaren arteko arrazoia (zatidura) da.Kotangentea (cotg). Angelu zorrotzaren kotangentea (cotg),
bere alboko katetuaren eta parekoaren arteko arrazoia (zatidura)
da, hots, tangentearen alderantzizkoa.Sekantea (sec). Angelu zorrotzaren sekantea (set), hipotenusaren
eta alboko katetuaren arteko arrazoia (zatidura) da, hots, kosinuaren
alderantzizkoa.Kosekantea (cosec). Angelu zorrotzaren kosekantea (cosec),
hipotenusaren eta pareko katetuaren arteko arrazoia (zatidura) da,
hots, sinuaren alderantzizkoa.
Jarraian, arrazoi edo erlazio bakoitzari dagokion formula ematen
da.
X. Arrazoi trigonometrikoen definizioak
 angelu zentrala hartzen da. Zirkunferentzian dagoen P puntu batetik, OX jatorrizko PM aldeari perpendikular lerro bat botatzen zaio eta PMO triangelu zuzena lortzen da.
angelu zentrala hartzen da. Zirkunferentzian dagoen P puntu batetik, OX jatorrizko PM aldeari perpendikular lerro bat botatzen zaio eta PMO triangelu zuzena lortzen da.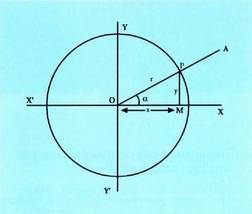 P puntuaren koordenatuak (x,y) moduan izendatzen dira eta OP
distantzia r erradio gisa.. , y eta r, hiru kopuru horien artean, 6 arrazoi daude, hiru zuzenekoak
eta hiru alderantzizkoak, eta arrazoi trigonometriko deitzen
dira.Sinua, ordenatuaren eta erradioaren arteko arrazoia da. Honela
adierazten da :
P puntuaren koordenatuak (x,y) moduan izendatzen dira eta OP
distantzia r erradio gisa.. , y eta r, hiru kopuru horien artean, 6 arrazoi daude, hiru zuzenekoak
eta hiru alderantzizkoak, eta arrazoi trigonometriko deitzen
dira.Sinua, ordenatuaren eta erradioaren arteko arrazoia da. Honela
adierazten da :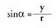 Kosinua, abzisaren eta erradioaren arteko arrazoia da.
Kosinua, abzisaren eta erradioaren arteko arrazoia da.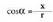 Tangentea, ordenatuaren eta abzisaren arteko arrazoia da.
Tangentea, ordenatuaren eta abzisaren arteko arrazoia da.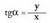 Kotangentea, abzisaren eta ordenatuaren arteko arrazoia da.
Kotangentea, abzisaren eta ordenatuaren arteko arrazoia da.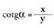 Sekantea, erradioaren eta abzisaren arteko arrazoia da.
Sekantea, erradioaren eta abzisaren arteko arrazoia da.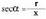 Kosekantea, erradioaren eta ordenatuaren arteko arrazoia da.
Kosekantea, erradioaren eta ordenatuaren arteko arrazoia da.
XI. Arrazoi trigonometrikoen irudikapen geometrikoa.
Gauza jakina da arrazoi goniometrikoak, bi zuzenkiren arteko
zatidurak direla, zenbaki abstraktuak dira, beraz ; baina zuzenki
bakar batez irudika daitezke, baldin eta triangelu zuzenak eraiki
eta erradioarentzat luzera-unitatea hartzen baldin bada, izan ere,
horrela, arrazoietako izendatzaileek bat balioko baitute. Bestela
esanda, zirkunferentzia goniometriko batean lan eginez gero,
arrazoi trigonometriko bakoitza zuzenki batez irudikatuko da.
Bedi XOA angelu zentrala unitatea erradiotzat eta O zentrotzat
dituen zirkunferentzia batean.
Zirkunferentzia horrek eta XOA angeluaren aldeak elkar ebakitzen
duten P puntutik, PM elkartzuta marratzen zaio OX ardatzari
eta baita lehen koadranteko jatorritik zirkunferentziari marraztutako
ukitzailea ere.
Dei deizaiogun a X O A angeluari.OC = OP = 1 dugu, beraz :
 Era berean, zirkunferentzia horrek eta XOA angeluaren aldeak elkar ebakitzen duten P puntutik, OY ri buruz zuta den
Era berean, zirkunferentzia horrek eta XOA angeluaren aldeak elkar ebakitzen duten P puntutik, OY ri buruz zuta den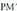 lerroa marratzen da eta baita lehen koadranteko tangentea ere B muturrean.
lerroa marratzen da eta baita lehen koadranteko tangentea ere B muturrean.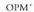 eta ODB angeluak XOA angeluaren berdinak dira, hau da,
eta ODB angeluak XOA angeluaren berdinak dira, hau da,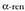 berdinak, izan ere, lerro paralelo artean kokatutako txandakako barneangeluak baitira.Orduan, OC = OP = OB = 1 da, beraz :
berdinak, izan ere, lerro paralelo artean kokatutako txandakako barneangeluak baitira.Orduan, OC = OP = OB = 1 da, beraz :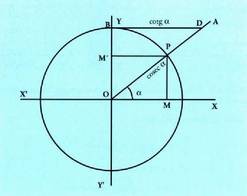 Laburpen-koadroa (ikus irudiak) :
Laburpen-koadroa (ikus irudiak) :
XII. Arrazoi trigonometrikoek lau koadranteetan dituzten zeinuak.
r erradioa beti bere balio absolutuarekin hartzen da, beraz, beti
positibotzat hartzen da.
Kosekante, sekante eta kotangentearen zeinuak, hurrenez hurren
sinu, kosinu eta tangenteak dituztenen alderantzizkoak direla kontuan
hartuta zehazten dira, beraz, hauek dituzten berberak izango
dituzte.
Aurreko atalean emandako definizioak kontuan hartuta, arrazoi
trigonometrikoen zeinuak, hartutako angeluaren muturreko aldea
koadrante edo zirkulu-laurdenaren araberakoak izango dira.
Horrela, sinuaren zeinua, arkuaren muturreko ordenatua, positiboa
da lehen eta bigarren koadranteetan eta negatiboa hirugarren
eta laugarrenetan. Kosekanteak, sinuaren alderantzizkoa denez,
haren zeinu berberak ditu.
Kosinuaren kasuan, dagokion arkuaren muturreko abzisa, lehen
eta laugarren koadranteetan da positiboa ordenatu-ardatzaren
eskuinaldean dagoelako ; aldiz, negatiboa izango da bigarren eta
hirugarren koadranteetan.
Tangentea berriz, positiboa izango da lehen eta hirugarren koadranteetan,
berari dagokion zuzenkia abzisa-ardatzaz goitik dagoelako
eta gainera koadrante horietan dira berdinak sinuaren eta
kosinuaren zeinuak.Jarraian, arrazoi trigonometrikoen zeinuak laburbilduta ematen
dira lau koadranteetan.
127
XIII. Angelu berberaren arrazoi trigonometrikoen arteko funtsezko erlazioak.
Gauza jakina da, alegia :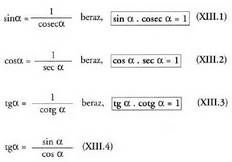 Zirkunferentzia goniometrikoan, hiru triangelu zuzen marraz
daitezke eta horietatik abiatuta, Pitagorasen teorema aplikatuz, bistakoak
dira ondoko erlazio hauek :
Zirkunferentzia goniometrikoan, hiru triangelu zuzen marraz
daitezke eta horietatik abiatuta, Pitagorasen teorema aplikatuz, bistakoak
dira ondoko erlazio hauek : Aurreko formula horiek, angelu baten 6 arrazoi trigonometrikoak
elkarlotzen dituzte beren artean eta bat ezagututa gainerako
bostak jakiteko aukera ematen dute.
Aurreko formula horiek, angelu baten 6 arrazoi trigonometrikoak
elkarlotzen dituzte beren artean eta bat ezagututa gainerako
bostak jakiteko aukera ematen dute.
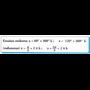
Angelu baten balio trigonometriko bat emanda, kalkulatu
gainerako arrazoiak.
Ebatzitako ariketak.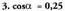 baldin bada, kalkulatu gainerako arrazoi trigonometrikoak, a lehen koadrantean dagoela jakinda.(XIII.5) formula erabiliz :
baldin bada, kalkulatu gainerako arrazoi trigonometrikoak, a lehen koadrantean dagoela jakinda.(XIII.5) formula erabiliz :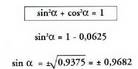 Emaitzak dituen bi zeinuetatik balio positiboa bakarrik hartuko
da kasu honetan, izan ere, ariketa-testuaren arabera, a lehen koadrantean
baitago.(XIII. 4) formula erabiliz :
Emaitzak dituen bi zeinuetatik balio positiboa bakarrik hartuko
da kasu honetan, izan ere, ariketa-testuaren arabera, a lehen koadrantean
baitago.(XIII. 4) formula erabiliz :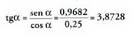 Alderantzizko arrazoiak berriz, aurreko balioetatik kalkulatzen
dira :
Alderantzizko arrazoiak berriz, aurreko balioetatik kalkulatzen
dira : Arrazoi guztien zeinuak positiboak dira, angelua lehen koadrantean
dago eta.
Arrazoi guztien zeinuak positiboak dira, angelua lehen koadrantean
dago eta.
Emaitzak : 4.
4.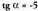 bada, kalkulatu gainerako arrazoi trigonometrikoak a laugarren koadrantean dagoela jakinda.(XIII. 6) formula erabiliz :
bada, kalkulatu gainerako arrazoi trigonometrikoak a laugarren koadrantean dagoela jakinda.(XIII. 6) formula erabiliz :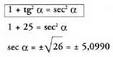 Izan daitezkeen bi zeinuetik, positiboa bakarrik hartuko dugu,
izan ere, angeluaren muturra laugarren koadrantean baitago ariketa-testuak
esaten duenez.(XIII. 2) formula erabiliz :
Izan daitezkeen bi zeinuetik, positiboa bakarrik hartuko dugu,
izan ere, angeluaren muturra laugarren koadrantean baitago ariketa-testuak
esaten duenez.(XIII. 2) formula erabiliz :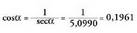 Sinuaren balioa kalkulatzeko, bi bide jarrai daitezke :a) (XIII.5) formula erabiliz :
Sinuaren balioa kalkulatzeko, bi bide jarrai daitezke :a) (XIII.5) formula erabiliz :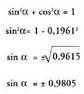 Sinuak dituen bi zeinuetatik, negatiboa bakarrik hartuko dugu
kontuan, izan ere, angeluaren muturra laugarren koadrantean baitago
.(XIII.4) formula erabiliz :
Sinuak dituen bi zeinuetatik, negatiboa bakarrik hartuko dugu
kontuan, izan ere, angeluaren muturra laugarren koadrantean baitago
.(XIII.4) formula erabiliz :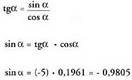 Alderantzizko arrazoien balioak, aurrez lortutako balioetatik ateratzen dira :
Alderantzizko arrazoien balioak, aurrez lortutako balioetatik ateratzen dira : Arrazoi trigonometrikoen zeinuak, laugarren koadranteari
dagozkionak dira.Emaitzak :
Arrazoi trigonometrikoen zeinuak, laugarren koadranteari
dagozkionak dira.Emaitzak : 5.
5. bada, kalkulatu gainerako arrazoi trigonometrikoak.
bada, kalkulatu gainerako arrazoi trigonometrikoak.
Ariketa honetan ez da adierazten angeluaren muturra zein koadrantetan dagoen kokatuta. Sinuaren zeinua positiboa denez, lehen edo bigarren koadrantean egon daiteke. Arrazoi trigonometrikoak kalkulatzeko egin beharreko kalkuluak errazteko, beren balio absolutuak bakarrik har daitezke eta gero, azkenean, zein koadrantetan ari garen kontuan hartuta zeinuak jarri.(XIII.5) formula erabiliz :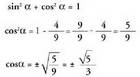 (XIII.4) formula erabiliz :
(XIII.4) formula erabiliz :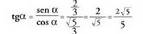 Alderantzizko arrazoien balioak, aurrez lortutako balioetatik ateratzen
dira :
Alderantzizko arrazoien balioak, aurrez lortutako balioetatik ateratzen
dira : Ebazpena :a)
Ebazpena :a)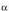 lehen koadrantean baldin badago :
lehen koadrantean baldin badago :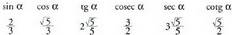 b)
b)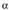 bigarren koadrantean baldin badago :
bigarren koadrantean baldin badago :
- Proposatutako ariketak
3. bada, kalkulatu gainerako arrazoi trigonometrikoak,
bada, kalkulatu gainerako arrazoi trigonometrikoak, bigarren koadrantean dagoela jakinda.
bigarren koadrantean dagoela jakinda.
4. -dela jakinda, kalkulatu gainerako arrazoi trigonometrikoak,
-dela jakinda, kalkulatu gainerako arrazoi trigonometrikoak, hirugarren koadrantean dagoela jakinda.
hirugarren koadrantean dagoela jakinda.
5.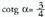
XIV. 0º , 90º , 180°, 270° eta 360°ko angeluen sinuek eta kosinuek dituzten balioak
Xv 30° eta 60°ko angeluen arrazoi trigonometrikoak
30°, 60° eta 45°ko angeluen arrazoi trigonometrikoak maiz
azaltzen dira problemen ebazketetan, batez ere Fisikan, beraz,
komenigarria da buruz jakitea, edota hobea oraindik, haien balioak
ateratzen jakitea. Ondoren, hori lortzeko urratsak datoz.
Bedi ABC triangelu aldekidea, L aldea duena eta bertan AC
aldeari BD lerro elkartzuta marratu zaio. Horrela, triangelua bi zati
berdinetan zatituta geratu da eta triangelu aldekidea bi triangelu
angeluzuzen berdinetan. BAD angeluak, 60° neurtzen ditu eta
ABD angeluak 30° ABC angeluaren erdia delako eta ABC angeluak
ere 60° dituelako.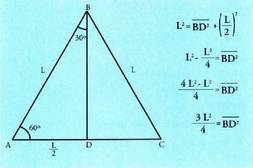 Pitagorasen teoremaren arabera, BD segmentuaren eta triangelu
aldekidearen L aldearen arteko erlazioa erabiliko dugu.
Pitagorasen teoremaren arabera, BD segmentuaren eta triangelu
aldekidearen L aldearen arteko erlazioa erabiliko dugu. Era berean lortzen dira :
Era berean lortzen dira :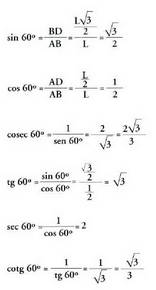 Aurreko emaitzetatik ondorioztatuta, beste ondorio honetara
iristen da :Angelu osagarrien sinua eta kosinua berdinak dira.• Adibideak:
Aurreko emaitzetatik ondorioztatuta, beste ondorio honetara
iristen da :Angelu osagarrien sinua eta kosinua berdinak dira.• Adibideak:
XVI. 45°ko angeluaren arrazoi trigonometrikoak.
Bedi ABCE karratua, L aldea duena eta bere diagonaletako
baten bitartez, BE-z adibidez, bi zati berdinetan zatitu dena.
Pitagorasen teoremaren bitartez, D diagonalaren eta karratuaren L
aldearen arteko erlazioa kalkulatuko da.
XVII. Arrazoi trigonometrikoak lehen koadrantera biltzea.
XVII.1. Zirkunferentzi kopuru osoko aldea duten angeluen arrazoi trigonometrikoak.
Zirkunferentzi kopuru osoko aldea duten angeluek, hala nola, 30°, 390°, 750° eta gisakoek adibidez, jatorri eta mutur berberak dituzte den-denek. Horren ondorioz, arrazoi trigonometriko guzti-guztiak berdinak dituzte. Baldin eta deitzen bazaio lehen koadranteko angeluari eta
deitzen bazaio lehen koadranteko angeluari eta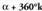 zirkunferentzi kopuru osoko aldea dutenei, beti ere k zenbaki arrunta izanik, ondoko hau idatz daiteke :
zirkunferentzi kopuru osoko aldea dutenei, beti ere k zenbaki arrunta izanik, ondoko hau idatz daiteke : • Adibideak:
• Adibideak:
XVII.2. 180°ko batura duten edota osagarriak diren angeluen arrazoi trigonometrikoak.
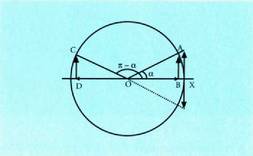 Angelu betegarriek berriz, 30° eta 150°, 45° eta 135°, 60° eta 120° adibidez, denek jatorri berbera dute, baina angeluetako batek bere muturra lehen koadrantean duen bitartean, besteak bigarren koadrantean du berea. Baldin eta lehen koadranteko angeluari
Angelu betegarriek berriz, 30° eta 150°, 45° eta 135°, 60° eta 120° adibidez, denek jatorri berbera dute, baina angeluetako batek bere muturra lehen koadrantean duen bitartean, besteak bigarren koadrantean du berea. Baldin eta lehen koadranteko angeluari deitzen bazaio eta
deitzen bazaio eta bere betegarriari, irudian ikusten denez, AOB eta COB triangeluak berdinak dira, beraz, angeluen sinu, kosinu eta tangenteek balio absolutu berbera dute, baina azken bi arrazoien eta beren alderantzizkoen zeinuak dira aldatzen direnak. Orduan, honako hauek dira beren arrazoi trigonometrikoak :
bere betegarriari, irudian ikusten denez, AOB eta COB triangeluak berdinak dira, beraz, angeluen sinu, kosinu eta tangenteek balio absolutu berbera dute, baina azken bi arrazoien eta beren alderantzizkoen zeinuak dira aldatzen direnak. Orduan, honako hauek dira beren arrazoi trigonometrikoak : • Adibideak :
• Adibideak :
- Proposatzen diren ariketak :
6. Adierazi ondorengo arrazoi hauek angelu zorrotzaren arabera
XVII.3. 180°ko edo n radianeko aldea duten angeluen arrazoi trigonometrikoak.
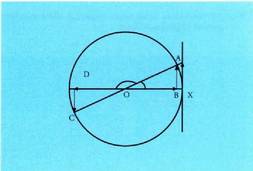 180 ° ko aldea duten angeluek, 30° eta 210°, 45 ° eta 225 ° , 60° eta 240° adibidez, denek jatorri berbera dute baina angelu batek bere muturra lehen koadrantean duen bitartean, besteak hirugarrenan du. Lehen koadranteko angeluari
180 ° ko aldea duten angeluek, 30° eta 210°, 45 ° eta 225 ° , 60° eta 240° adibidez, denek jatorri berbera dute baina angelu batek bere muturra lehen koadrantean duen bitartean, besteak hirugarrenan du. Lehen koadranteko angeluari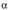 deitzen badiogu eta
deitzen badiogu eta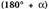 hirugarren koadrantean dagoenari, irudian ikusten denez, AOB eta COD triangeluak berdinak dira, beraz, angelu horien sinu, kosinu eta tangenteak, balio absolutu berbera dute eta sinuen, kosinuen nahiz beren alderantzizkoen zeinuak bakarrik dira alderantzizkoak. Beren arrazoi trigonometrikoak, hauek dira :
hirugarren koadrantean dagoenari, irudian ikusten denez, AOB eta COD triangeluak berdinak dira, beraz, angelu horien sinu, kosinu eta tangenteak, balio absolutu berbera dute eta sinuen, kosinuen nahiz beren alderantzizkoen zeinuak bakarrik dira alderantzizkoak. Beren arrazoi trigonometrikoak, hauek dira : • Adibideak:
• Adibideak:
- Proposatzen diren ariketak :
7. Adierazi ondorengo arrazoiak angelu zorrotzaren arabera :
XVII.4. 360°ko batura duten angeluen arrazoi trigonometrikoak.
360°ko batura duten bi angeluren izen bereko arrazoi trigonometrikoak,
berdinak dira balio absolutuetan, baina kosinua eta
sekantea bakarrik dira zeinu berekoak (abzisaren baitakoak bakarrik
direlako) eta gainerakoek aurkako zeinua dute. • Adibideak :
• Adibideak :
XVII.5. Aurkako angeluen arrazoi trigonometrikoak.
.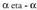 aurkako angeluek, arrazoi trigonometriko guztiak balio absolutu berdinekoak dituzte, baina zeinu berekoak bi baizik ez : kosinua eta sekantea. Formulak era honetan idatz daitezke :
aurkako angeluek, arrazoi trigonometriko guztiak balio absolutu berdinekoak dituzte, baina zeinu berekoak bi baizik ez : kosinua eta sekantea. Formulak era honetan idatz daitezke : • Adibideak:
• Adibideak:
XVII.6. 90 ° ko batura duten edota osagarriak diren angeluen arrazoi trigonometrikoak.
Angelu osagarrietan berdintza hauek betetzen dira : Aurreko formuletan ikusten denez, angelu zorrotz baten funtzio
trigonometriko bakoitza, angelu osagarriaren izen bereko kofuntzioaren
berdina da.Ko-sinuak, angelu osagarriaren sinua esan nahi du eta kideko
esanahiak dituzte beste kofuntzioek ere (tangente/ko-tangente eta
sekante/ko-sekante).
Aurreko formuletan ikusten denez, angelu zorrotz baten funtzio
trigonometriko bakoitza, angelu osagarriaren izen bereko kofuntzioaren
berdina da.Ko-sinuak, angelu osagarriaren sinua esan nahi du eta kideko
esanahiak dituzte beste kofuntzioek ere (tangente/ko-tangente eta
sekante/ko-sekante). • Adibideak :
• Adibideak :
XVII.7. 90° ko aldea duten angeluen arrazoi trigonometrikoak.
ABO eta CDO triangeluak zuzenak dira eta gainera COD eta BAO angeluak berdinak dauzkate, izan ere, beren artean elkartzutak diren aldeez baitaude eratuta. Baldintza horiek betetzeak, triangeluak berdinak direla esan nahi du eta, balio absolutuetan, OB segmentua DC-ren berdina da eta BA berriz OD-ren berdina.Horrek, ondoko hau idazteko aukera ematen du :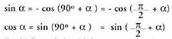 Eta bi formula horiek beren artean zatituta, ondoko hau lortzen da :
Eta bi formula horiek beren artean zatituta, ondoko hau lortzen da :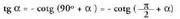 Era berean lortzen dira :
Era berean lortzen dira :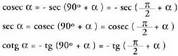 Beraz, bi angeluk 90°ko aldea baldin badute, bataren funtzioak, balio absolututan, bestearen funtzioen berdinak dira, baina zeinu bera,
Beraz, bi angeluk 90°ko aldea baldin badute, bataren funtzioak, balio absolututan, bestearen funtzioen berdinak dira, baina zeinu bera,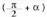 angeluaren sinuak eta kosekanteak dute.• Adibideak :
angeluaren sinuak eta kosekanteak dute.• Adibideak :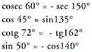 XVTI. puntuko ataletan emandako formulen bitartez era ikusten
da, alegia, edozein angeluren arrazoi trigonometrikoak, lehen koadranteko
angelu batenetara laburbildu ahal izateko, beraz, horretarako,
ezinbestekoa da arrazoi trigonometrikoek lau koadranteetan
dituzten zeinuak zeintzuk diren jakitea (ikus XII. puntua).• Adibideak:
XVTI. puntuko ataletan emandako formulen bitartez era ikusten
da, alegia, edozein angeluren arrazoi trigonometrikoak, lehen koadranteko
angelu batenetara laburbildu ahal izateko, beraz, horretarako,
ezinbestekoa da arrazoi trigonometrikoek lau koadranteetan
dituzten zeinuak zeintzuk diren jakitea (ikus XII. puntua).• Adibideak:
Kalkulagailua nola erabili
Angeluak neurtzeko banakoei buruzko atalean ikusi denez, hiru banako desberdin daude angelu baten neurria adierazteko : gradu hirurogeitarrak, radianak eta gradu ehundarrak, beraz, lan egiteko zein banako erabiliko den erabaki behar da lehenik. Kalkulagailu batzuetan, bada tekla bat D.R.G. izenekoa ; tekla horrek zein banako erabili zuzenean aukeratzen uzten du. Gainera, leihoan azalduko da : DEG gradu hirurogeitarrentzat, RAD radianentzat eta GRA gradu ehundarrentzat.
Beste kalkulagailu batzuek berriz, badute tekla bat MODE izenekoa ; hori sakatzean beste tekla bat sakatu behar da atzetik, 4a adibidez, leihoan DEG lortzeko.
MODE sakatu eta 5 tekla sakatzen bada atzetik, RAD azaltzen da leihoan. Zenbaki edo gako horiek ordea, ez dira berdinak kalkulagailu guztietan eta modu desberdinei dagozkien gakoak, bertan azaldu ohi dira, beraz, edozein kalkulu egin aurretik, beti ere lan egiteko zein kalkulagailu mota dugun ongi aztertzea komeni da. teklak, gradu hirurogeitarretan emandako angelu bat modu hamartarrean jartzeko balio du. Alderantzizko eragiketa egin nahi denean, hau da, gradu hirurogeitarretatik modu hamartarrera pasa nahi denean,
teklak, gradu hirurogeitarretan emandako angelu bat modu hamartarrean jartzeko balio du. Alderantzizko eragiketa egin nahi denean, hau da, gradu hirurogeitarretatik modu hamartarrera pasa nahi denean, tekla sakatzen da.• Adibidez: Bedi 28° 35' 27 angelua. Kalkulagailuarekin eragiketak egiteko, saka ezazu zenbaki bakoitza
tekla sakatzen da.• Adibidez: Bedi 28° 35' 27 angelua. Kalkulagailuarekin eragiketak egiteko, saka ezazu zenbaki bakoitza teklaz jarraituta.
teklaz jarraituta.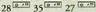 eta leihoan,
eta leihoan,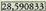 azalduko da, izan ere, hori baita angeluaren balioa zenbaki hamartarretan adierazita. Emaitza hori gradu hirurogeitarretan adierazi nahi baldin bada,
azalduko da, izan ere, hori baita angeluaren balioa zenbaki hamartarretan adierazita. Emaitza hori gradu hirurogeitarretan adierazi nahi baldin bada,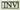 sakatzen da eta jarraian
sakatzen da eta jarraian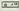 tekla, hau da :
tekla, hau da :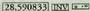 eta leihoan
eta leihoan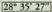 azaltzen da, hogeita zortzi gradu, hogeita hamabost minutu eta hogeita zazpi segundo, irakurtzeko.
azaltzen da, hogeita zortzi gradu, hogeita hamabost minutu eta hogeita zazpi segundo, irakurtzeko.
Kalkulagailuetan badira beste tekla batzuk ere trigonometriako kalkuluak egiteko oso erabilgarriak direnak. Tekla horiek honako hauek dira : eta
eta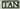 ; sinuari, kosinuari eta tangenteari dagozkie.• Adibidez: Bedi 50°ko angelua eta haren sinuaren balioa jakin nahi da.
; sinuari, kosinuari eta tangenteari dagozkie.• Adibidez: Bedi 50°ko angelua eta haren sinuaren balioa jakin nahi da.
Lehendabizi, zein unitatetan lan egin behar dugun kontrolatu behar da. Leihoan DEG azaltzen bada, angelua gradu hirurogeitarretan neurtzen ari den seinale da.
50 sakatzen da; ondoren,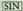 tekla sakatu behar da eta
tekla sakatu behar da eta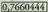 azalduko da leihoan, hain zuzen ere, 50°ko angeluaren sinuak balio duena. Sinuaren ordez kosinua edota tangentea jakin nahi baldin bada, aurreko kasuan bezala jokatuko da, baina arrazoi trigonometriko horietako bakoitzari dagokion tekla sakatuz.
azalduko da leihoan, hain zuzen ere, 50°ko angeluaren sinuak balio duena. Sinuaren ordez kosinua edota tangentea jakin nahi baldin bada, aurreko kasuan bezala jokatuko da, baina arrazoi trigonometriko horietako bakoitzari dagokion tekla sakatuz.
Sinuaren, kosinuaren eta tangentearen teklek, angeluaren balioa kalkulatzeko ere balio dute, angelu horren arrazoi trigonometrikoren bat jakina baldin bada.• Adibidea: Badakigu jakin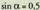 dela. Zein da a angeluaren balioa?
Lehendabizi lan egiteko erabakitako unitatea kontrolatu
behar da. Gero, 0.5 sakatzen da eta jarraian
dela. Zein da a angeluaren balioa?
Lehendabizi lan egiteko erabakitako unitatea kontrolatu
behar da. Gero, 0.5 sakatzen da eta jarraian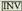 eta
eta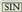 sakatu behar dira. Leihoan 30 azaltzen da; horrek zera esan
nahi du, a angeluak 30 gradu hirurogeitar balio dituela baldin
eta banako horrekin ari bagara lanean ; leihoan DEG
jartzen duen ikusiz egiaztatu behar da hori.
sakatu behar dira. Leihoan 30 azaltzen da; horrek zera esan
nahi du, a angeluak 30 gradu hirurogeitar balio dituela baldin
eta banako horrekin ari bagara lanean ; leihoan DEG
jartzen duen ikusiz egiaztatu behar da hori.
0.5 sakatu ondoren eta jarrai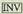 eta
eta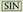 ,
,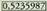 agertzen bada, horrek zera esan nahi du,
agertzen bada, horrek zera esan nahi du,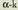 0,5235987 radianeko balioa duela, hain zuzen ere leihoan
RAD unitatea azaltzen delako.
0,5235987 radianeko balioa duela, hain zuzen ere leihoan
RAD unitatea azaltzen delako.
XVIII. Angeluaren arrazoietako bat jakinik, kalkulatu angelua.
Angelu baten edozein arrazoi trigonometriko emanik, angelua ez
du arrazoi bakar horrek zehazten, izan ere, bai baitaude 360° baino
txikiagoak diren bi angelu arrazoi hori berbera dutenak. Hori xeragatik
da, alegia, sinuaren edota kosekantearen balio positibo jakin
bati, lehen edo bigarren koadrantean kokatutako bi angelu dagozkiola;
balioa negatiboa bada berriz, hirugarren eta laugarren koadranteetan
kokatutako bi angelu dagozkio hurrenez hurren.1. adibidea.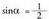 emanda, kalkulatu
emanda, kalkulatu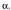 Ebazpena: 360° baino txikiagoak diren angeluak hartzen badira, bi emaitza izango ditugu :
Ebazpena: 360° baino txikiagoak diren angeluak hartzen badira, bi emaitza izango ditugu :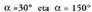 360° baino txikiagoak diren angeluak hartzen badira, orokorki :
360° baino txikiagoak diren angeluak hartzen badira, orokorki : Beraz, badira 360° baino txikiagoak diren bi angelu sinu berbera
dutenak ; eta beste kopuru mugagabe bat 360°z goitikoak hartzen
badira; azken horiek, formulako k letrari balio positibo eta
negatibo guztiak emanez lortzen dira.Tangentearen edota kotangentearen balio positibo baten balioari,
lehen eta hirugarren koadranteetan kokatutako angeluak dagozkio
eta beren artean 180°ko aldea dute ; emandako balioa negatiboa
baldin bada, angeluak bigarren eta laugarren koadranteetan
egongo dira.2. adibidea.
Beraz, badira 360° baino txikiagoak diren bi angelu sinu berbera
dutenak ; eta beste kopuru mugagabe bat 360°z goitikoak hartzen
badira; azken horiek, formulako k letrari balio positibo eta
negatibo guztiak emanez lortzen dira.Tangentearen edota kotangentearen balio positibo baten balioari,
lehen eta hirugarren koadranteetan kokatutako angeluak dagozkio
eta beren artean 180°ko aldea dute ; emandako balioa negatiboa
baldin bada, angeluak bigarren eta laugarren koadranteetan
egongo dira.2. adibidea.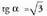 emanik, kalkulatu a.Ebazpena : Balio hori adierazten duten 360° baino txikiagoak diren bi angeluak, zera dira:
emanik, kalkulatu a.Ebazpena : Balio hori adierazten duten 360° baino txikiagoak diren bi angeluak, zera dira: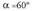 eta
eta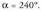 .
.
360° baino txikiagoak diren angeluak hartzen badira kontuan, orokorki zera izango dugu : Bi emaitza hauek, formula bakar batean laburbil daitezke :
Bi emaitza hauek, formula bakar batean laburbil daitezke :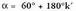 horretan
horretan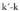 balio oso guztiak hartzen dituela.
balio oso guztiak hartzen dituela.
Formula honetan ikus daitekeenez, tangentea 180°-z ( radianez) behin errepikatu egiten da ; beraz, tangentearen aldia edo periodoa, 180° (
radianez) behin errepikatu egiten da ; beraz, tangentearen aldia edo periodoa, 180° ( radian) da.Kosinuaren edota sekantearen balio positibo jakin bati, bi angelu
elkarren parez pareko edo angelu kontrajarri dagozkio, lehen eta
laugarren koadranteetan kokatuak. Emandako balioa negatiboa
baldin bada berriz, angeluak, bigarren eta hirugarren koadranteetan
egongo dira hurrenez hurren.3. adibidea.
radian) da.Kosinuaren edota sekantearen balio positibo jakin bati, bi angelu
elkarren parez pareko edo angelu kontrajarri dagozkio, lehen eta
laugarren koadranteetan kokatuak. Emandako balioa negatiboa
baldin bada berriz, angeluak, bigarren eta hirugarren koadranteetan
egongo dira hurrenez hurren.3. adibidea.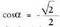 emanik, kalkulatu
emanik, kalkulatu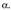 .
.
Ebazpena: balio hori duten 360° baino txikiagoko bi angeluak,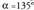 eta
eta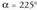 dira.360° baino txikiagoak hartzen badira kontuan, orokorki ondorengoa
izango dugu :
dira.360° baino txikiagoak hartzen badira kontuan, orokorki ondorengoa
izango dugu : Ebatzitako. ariketak.6. Kalkulatu x-en balioa ondoko ekuazio hauetan :
Ebatzitako. ariketak.6. Kalkulatu x-en balioa ondoko ekuazio hauetan : Emaitzak:
Emaitzak: 7. Zirkunferentzia goniometriko baten lehen koadranteko zein
angelu dira egokiak ondoko angelu hauen arrazoi trigonometrikoak
kalkulatzeko?
7. Zirkunferentzia goniometriko baten lehen koadranteko zein
angelu dira egokiak ondoko angelu hauen arrazoi trigonometrikoak
kalkulatzeko?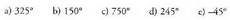 Ebazpena :a)
Ebazpena :a) eta
eta batura dutelako.b)
batura dutelako.b)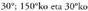 angeluak angelu betegarriak direlako.c)
angeluak angelu betegarriak direlako.c)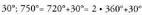 delako.d)
delako.d)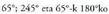 aldea edo diferentzia dutelako.e)
aldea edo diferentzia dutelako.e)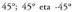 angelu aurkajarriak edota parez parekoak direlako.8. Adierazi ondoko arrazoi trigonometriko hauek, lehen koadranteko
angelu bati dagozkionen bitartez :
angelu aurkajarriak edota parez parekoak direlako.8. Adierazi ondoko arrazoi trigonometriko hauek, lehen koadranteko
angelu bati dagozkionen bitartez :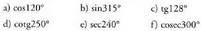 Ebazpena :
Ebazpena : 9. Bedi a lehen koadrantean kokatutako angelu bat. Badakigu jakin,
9. Bedi a lehen koadrantean kokatutako angelu bat. Badakigu jakin, dela. Kalkulatu, a-ren baliorik jakin gabe, ondoko hauen balioak :
dela. Kalkulatu, a-ren baliorik jakin gabe, ondoko hauen balioak :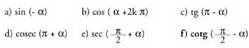 Lehendabizi,
Lehendabizi, inserted text
inserted text Jarraian, taula batean jartzen dira lortutako emaitzak :
Jarraian, taula batean jartzen dira lortutako emaitzak : Ebazpena :
Ebazpena :
- Proposatzen diren ariketak :
8. a) emanik,
emanik,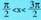 baldin bada, kalkulatu x.b)
baldin bada, kalkulatu x.b)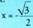 emanik,
emanik, baldin bada, kalkulatu x.9. Zenbat balio eduki ditzake
baldin bada, kalkulatu x.9. Zenbat balio eduki ditzake angeluak 720° baino txikiagoak,
angeluak 720° baino txikiagoak,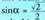 baldin bada. Zein koadrantetan daude angeluak?10. Zein kuadrantetan dago angelu bat sinua eta tangentea
biak negatiboak baditu.11. Osa ezazu ondoko taula, 126° ; 234° ; 306° ; -54° ; 36°
eta 144°ko angeluen arrazoi trigonometrikoekin.
baldin bada. Zein koadrantetan daude angeluak?10. Zein kuadrantetan dago angelu bat sinua eta tangentea
biak negatiboak baditu.11. Osa ezazu ondoko taula, 126° ; 234° ; 306° ; -54° ; 36°
eta 144°ko angeluen arrazoi trigonometrikoekin.
XIX. 0 eta 2n radian (0º eta 360º) artean dauden angeluen arrazoi trigonometrikoak.
XX: Funtzio zirkularrak
Koordenatu ardatz kartesiar batzuetan, abzisek radianetan adierazitako angeluen balioak izanik, aurreko koadroan jasotako bikote multzoa irudikatzen bada, angeluaren balioa (argumentua edo aldagaia) eta dagokion arrazoi trigonometrikoa hartuta, funtzio zirkularrak lortzen dira ; zirkunferentzia trigonometrikoan definitu direlako ematen zaie izen hori. Angelu baten sinua berari dagokion arkuaren muturreko ordenatuak irudikatuta dagoela gogoratuz gero (XI. puntua), aise ulertuko da sinuaren eta kosinuaren balioak 1 eta -1 balioen artean bakarrik egon daitezkeela .
XX.1.
 Radianetan adierazitako angeluen balioek eta angelu horiei
dagozkien sinuek eratutako puntuen multzoa koordenatu ardatzetan
irudikatzean, sinusoidea lortzen da.
Radianetan adierazitako angeluen balioek eta angelu horiei
dagozkien sinuek eratutako puntuen multzoa koordenatu ardatzetan
irudikatzean, sinusoidea lortzen da.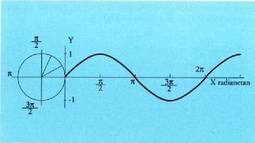 Badaude zenbait gertakari, esaterako uhin higiduraren azterketa edo ikasketa, sinu funtzioak
Badaude zenbait gertakari, esaterako uhin higiduraren azterketa edo ikasketa, sinu funtzioak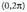 tartearen ezkerrerantz edo eskuinerantz hedatzen diren balioentzat zentzua dutenak. Kasu horietan, XVII. puntuan ikusi bezala, angeluen balioek zirkunferentzia kopuru oso baten aldea dutenean, a angeluaren arrazoi trigonometrikoak,
tartearen ezkerrerantz edo eskuinerantz hedatzen diren balioentzat zentzua dutenak. Kasu horietan, XVII. puntuan ikusi bezala, angeluen balioek zirkunferentzia kopuru oso baten aldea dutenean, a angeluaren arrazoi trigonometrikoak,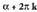 angeluen berberak dira. Gauza bera gertatzen da angelu negatiboentzat, alegia, a angeluaren arrazoi trigonometrikoak,
angeluen berberak dira. Gauza bera gertatzen da angelu negatiboentzat, alegia, a angeluaren arrazoi trigonometrikoak, angeluaren berberak direla. Beraz, sinusoidea, lerro zuzen erreal osoan zehar definituta dago eta bere irudia hau da :
angeluaren berberak direla. Beraz, sinusoidea, lerro zuzen erreal osoan zehar definituta dago eta bere irudia hau da :
XX.2.
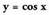 Sinusoidea lortzeko erabili den bidearen antzera jokatzen bada
baina kosinuaren balioak erabiliz, kosinusoidea lortzen da.
Sinusoidea lortzeko erabili den bidearen antzera jokatzen bada
baina kosinuaren balioak erabiliz, kosinusoidea lortzen da.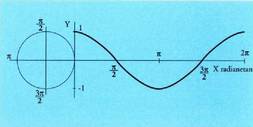 Sinu funtzioarekin gertatzen den bezalaxe, badaude gertakariak kosinu funtzioak
Sinu funtzioarekin gertatzen den bezalaxe, badaude gertakariak kosinu funtzioak tartearen ezkerrerantz edo eskuinerantz hedatzen diren balioentzat zentzua duenak.Aurreko atalean bezalaxe, a angeluaren arrazoi trigonometrikoak,
tartearen ezkerrerantz edo eskuinerantz hedatzen diren balioentzat zentzua duenak.Aurreko atalean bezalaxe, a angeluaren arrazoi trigonometrikoak, eta
eta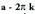 angeluen berberak dira. Beraz, kosinusoidea lerro zuzen erreal osoan zehar definituta dago eta bere irudia ondorengo hau du :
angeluen berberak dira. Beraz, kosinusoidea lerro zuzen erreal osoan zehar definituta dago eta bere irudia ondorengo hau du : Aurreko bi grafikoetan ikus daitekeenez, eremua, hau da, sinu eta kosinu funtzioetan x aldagaiak har ditzakeen balioen multzoa, R (zenbaki errealen multzoa) da. Sinu eta kosinu funtzioak, jarraiak eta periodikoak dira ; horrek zera esan nahi du, alegia, aldizka errepikatzen diren arku berdinen segida mugagabe batez daudela eratuta. Sinuaren eta kosinuaren periodoa (aldia)
Aurreko bi grafikoetan ikus daitekeenez, eremua, hau da, sinu eta kosinu funtzioetan x aldagaiak har ditzakeen balioen multzoa, R (zenbaki errealen multzoa) da. Sinu eta kosinu funtzioak, jarraiak eta periodikoak dira ; horrek zera esan nahi du, alegia, aldizka errepikatzen diren arku berdinen segida mugagabe batez daudela eratuta. Sinuaren eta kosinuaren periodoa (aldia)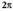 da, izan ere, ondorengoa betetzen baita :
da, izan ere, ondorengoa betetzen baita :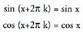
XX.3.
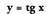 Sinu funtzioa lortzeko erabilitakoaren kideko modua erabiliz gero, baina oraingoan tangenteari dagozkion balioak erabiliz, zera ikusten da, alegia,
Sinu funtzioa lortzeko erabilitakoaren kideko modua erabiliz gero, baina oraingoan tangenteari dagozkion balioak erabiliz, zera ikusten da, alegia,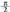 balioko angeluarentzat tangentea ez dagoela definituta. Angeluaren balioa Otik
balioko angeluarentzat tangentea ez dagoela definituta. Angeluaren balioa Otik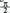 baliora handituz doanean, tangentea positiboa da, mugarik gabe handitzen da :
baliora handituz doanean, tangentea positiboa da, mugarik gabe handitzen da : adierazten da ikurren bidez. Angelua
adierazten da ikurren bidez. Angelua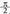 radian baino handixeagoa bada, tangentea orain negatiboa da angelua bigarren koadrantekoa delako, baina mugagabea izaten jarraitzen du ; ikur bidez
radian baino handixeagoa bada, tangentea orain negatiboa da angelua bigarren koadrantekoa delako, baina mugagabea izaten jarraitzen du ; ikur bidez adierazten da. Angeluak handitzen jarraitu eta
adierazten da. Angeluak handitzen jarraitu eta radianeko balioa izatera hurbiltzen doan heinean, tangentearen balioa zerorantz doa.
radianeko balioa izatera hurbiltzen doan heinean, tangentearen balioa zerorantz doa.
Angeluak eta
eta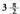 arteko balioak dituenean, tangenteak lehen koadrantean bezalakoxe egoera du, hau da, angeluaren balioa
arteko balioak dituenean, tangenteak lehen koadrantean bezalakoxe egoera du, hau da, angeluaren balioa baliorantz hurbiltzean, tangentea berriz ere mugagabea izatera pasatzen da. Laugarren koadrantean berriz, bigarren koadrantean ikusia errepikatzen da berriro. Beraz, tangente funtzioa, ondoren adierazten den moduan irudikatuko da :
baliorantz hurbiltzean, tangentea berriz ere mugagabea izatera pasatzen da. Laugarren koadrantean berriz, bigarren koadrantean ikusia errepikatzen da berriro. Beraz, tangente funtzioa, ondoren adierazten den moduan irudikatuko da :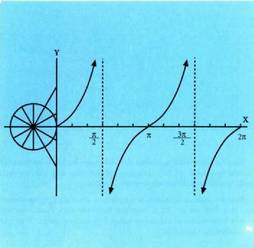 Sinu eta kosinu funtzioetan bezalaxe, badaude gertakariak tangente funtzioak
Sinu eta kosinu funtzioetan bezalaxe, badaude gertakariak tangente funtzioak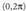 tartetik kanpo hedatzen diren balioentzat zentzua dutenak.
tartetik kanpo hedatzen diren balioentzat zentzua dutenak.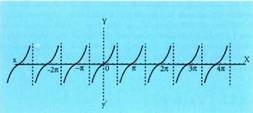 Grafikoan ikus daitekeenez, tangentearen periodoa
Grafikoan ikus daitekeenez, tangentearen periodoa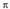 da, izan ere,
da, izan ere,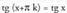 baita eta tangentearen eremua
baita eta tangentearen eremua , hau da,
, hau da,
Nola kalkula daiteke emandako funtzio zirkular jakin baten periodoa?
Batzuetan, funtzioa emanda, periodoa kalkulatu behar da. Ondoren, adibide batzuek ematen dira eta jarraitu beharreko urratsak adierazten dira.
Ikusi bezala, sinu eta kosinu funtzioen periodoa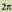 da, eta tangentearena, berriz,
da, eta tangentearena, berriz, Funtzioa
Funtzioa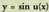 edo
edo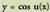 motakoa baldin bada, orduan ondoko berdinketa hau egiten da :
motakoa baldin bada, orduan ondoko berdinketa hau egiten da : Funtzioa
Funtzioa motakoa baldin bada, berdinketa orduan ondoko modu honetan gelditzen da berdinketa :
motakoa baldin bada, berdinketa orduan ondoko modu honetan gelditzen da berdinketa : 1. adibidea
1. adibidea 2. adibidea
2. adibidea 3. adibidea
3. adibidea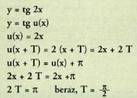 4. adibidea
4. adibidea
XX.4.
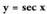 Sekante funtzioaren aldaketak, tangente funtzioa aztertuz batera
ikus daitezke. Hain zuzen ere, XI. atalean ikusi denez, sekanteak,
tangenteak eta zirkunferentzia goniometrikoaren erradioak triangelu
zuzena eratzen dute. Horrela, tangentea handitzen denean,
sekantea ere handitu egiten da, baina ez ahaztu, sekanteak, kosinuaren
alderantzizko funtzioa denez, zeinu positiboak izango
dituela lehen eta laugarren koadranteetan. Gainera, sekante funtzioak
ez du onartzen 1 eta - 1 balioen arteko baliorik.
Sekante funtzioaren aldaketak, tangente funtzioa aztertuz batera
ikus daitezke. Hain zuzen ere, XI. atalean ikusi denez, sekanteak,
tangenteak eta zirkunferentzia goniometrikoaren erradioak triangelu
zuzena eratzen dute. Horrela, tangentea handitzen denean,
sekantea ere handitu egiten da, baina ez ahaztu, sekanteak, kosinuaren
alderantzizko funtzioa denez, zeinu positiboak izango
dituela lehen eta laugarren koadranteetan. Gainera, sekante funtzioak
ez du onartzen 1 eta - 1 balioen arteko baliorik.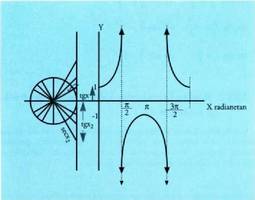 Aurreko irudian ikus daiteke sekantea, tangentea bezalaxe,
Aurreko irudian ikus daiteke sekantea, tangentea bezalaxe,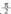 kopuru bakoitiz biderkatutako balioa duten
kopuru bakoitiz biderkatutako balioa duten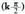 angeluen balioentzat ez dagoela definituta.Sekantearen periodoa
angeluen balioentzat ez dagoela definituta.Sekantearen periodoa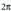
XX.5.
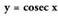 Aurreko kasuan bezalaxe, kosekante funtzioaren aldaketak kotangente funtzioarenak aztertzen diren une berean azter daitezke. Hain zuzen ere, XI. atalean ikusia den moduan, kosekanteak, kotangenteak eta zirkunferentzia goniometrikoaren erradioak triangelu zuzena eratzen dutela. Kotangentea handitzen denean, kosekantea ere handitu egiten da, baina ez da ahaztu behar kosekanteak, sinuaren alderantzizko funtzioa denez, lehen eta bigarren koadranteetan :einu positiboa izango duela. Gainera, kosekante funtzioak, ez du 1 eta - 1 balioen artean kokatutako baliorik onartzen.
Aurreko kasuan bezalaxe, kosekante funtzioaren aldaketak kotangente funtzioarenak aztertzen diren une berean azter daitezke. Hain zuzen ere, XI. atalean ikusia den moduan, kosekanteak, kotangenteak eta zirkunferentzia goniometrikoaren erradioak triangelu zuzena eratzen dutela. Kotangentea handitzen denean, kosekantea ere handitu egiten da, baina ez da ahaztu behar kosekanteak, sinuaren alderantzizko funtzioa denez, lehen eta bigarren koadranteetan :einu positiboa izango duela. Gainera, kosekante funtzioak, ez du 1 eta - 1 balioen artean kokatutako baliorik onartzen.
XX.6.
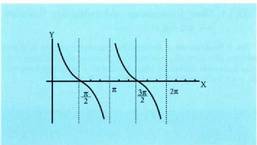 Aurreko irudietan ikus daiteke kosekantea, kotangentea bezala, ez dagoela definituta
Aurreko irudietan ikus daiteke kosekantea, kotangentea bezala, ez dagoela definituta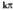 balioak dituzten angeluentzat.
balioak dituzten angeluentzat.
Kosekantearen periodoa, sinuaren kasuan bezalaxe,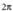 da ; hala ere, kotangentearen periodoa
da ; hala ere, kotangentearen periodoa
XXI. Alderantzizko funtzio zirkularrak
.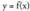 zuzeneko funtzioa emanik,
zuzeneko funtzioa emanik,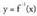 funtzioa haren alderantzizko funtzioa dela esaten da.
funtzioa haren alderantzizko funtzioa dela esaten da.
Funtzio bat beste baten alderantzizkoa da, baldin eta lehenengoan mendekoa den aldagaia bigarrenean aldagai aske bada edota alderantzizkoa gertatzen bada.• Adibidea :Bedi zuzeneko funtzioa.Aldagai askea askatu eta honako hau geldituko da :
zuzeneko funtzioa.Aldagai askea askatu eta honako hau geldituko da :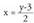 Beraz, alderantzizko funtzioa, izango da.
Beraz, alderantzizko funtzioa, izango da.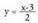 Zuzeneko funtzioaren eta alderantzizko funtzioaren grafikoak,
lehen koadranteko (eta hirugarreneko) erdikariarekiko
simetrikoak dira.• Adibidea :
Zuzeneko funtzioaren eta alderantzizko funtzioaren grafikoak,
lehen koadranteko (eta hirugarreneko) erdikariarekiko
simetrikoak dira.• Adibidea :
XXI.1. Sinu funtzioaren alderantzizko funtzioa.
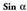 funtzioaren alderantzizko funtzioari arc sin a esaten zaio eta arku sinu alfa irakurtzen da. Funtzio hori, sinuaren funtziotik abiatuta lortzen da lehen koadranteko erdikariarekiko, hau da, y = x lerro zuzenarekiko, simetriaren bitartez.
funtzioaren alderantzizko funtzioari arc sin a esaten zaio eta arku sinu alfa irakurtzen da. Funtzio hori, sinuaren funtziotik abiatuta lortzen da lehen koadranteko erdikariarekiko, hau da, y = x lerro zuzenarekiko, simetriaren bitartez.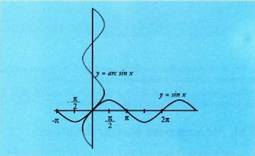 Funtzio bat lortzeko grafikoa unibokoa izan behar duela gogoratuz,
hau da, x-en balio bakoitzak y-ren balio bakar izan behar
duela, ulertuko da noski sinuaren alderantzizko funtzioaren zati
posible guztietatik, bat aukeratu behar dela.
Funtzio bat lortzeko grafikoa unibokoa izan behar duela gogoratuz,
hau da, x-en balio bakoitzak y-ren balio bakar izan behar
duela, ulertuko da noski sinuaren alderantzizko funtzioaren zati
posible guztietatik, bat aukeratu behar dela. tarteari dagokiona hartzeko ohitura dago.
tarteari dagokiona hartzeko ohitura dago. 1 eta -1 balioen artean kokatuta dagoen moduan, arc sin a ere hortik hartuko ditu balioak eta orduan arc sin a funtzioa ondorengo era honetan definituko dugu :
1 eta -1 balioen artean kokatuta dagoen moduan, arc sin a ere hortik hartuko ditu balioak eta orduan arc sin a funtzioa ondorengo era honetan definituko dugu :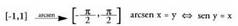 Aurretik esandakoaren arabera, ondorengoak beteko dira :
Aurretik esandakoaren arabera, ondorengoak beteko dira :
XXI.2. Kosinu funtzioaren alderantzizko funtzioa.
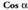 funtzioaren alderantzizko funtzioari
funtzioaren alderantzizko funtzioari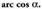 esaten zaio eta arku kosinu alfa irakurtzen da. Funtzio hori, aurreko kasuan bezalaxe, kosinuarenetik abiatuta lortzen da, lehen koadranteko erdikariarekiko simetriaren bitartez.
esaten zaio eta arku kosinu alfa irakurtzen da. Funtzio hori, aurreko kasuan bezalaxe, kosinuarenetik abiatuta lortzen da, lehen koadranteko erdikariarekiko simetriaren bitartez.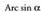 funtzioa bezalaxe, unibokoa izan behar du funtzio hau ere eta alderantzizko funtzioaren zati posible guztietatik, bat hautatu behar da. Normalean,
funtzioa bezalaxe, unibokoa izan behar du funtzio hau ere eta alderantzizko funtzioaren zati posible guztietatik, bat hautatu behar da. Normalean, tarteari dagokiona hartzen da.
tarteari dagokiona hartzen da.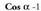 Cos a -1 eta 1 artean kokatuta dagoen moduan, arc cos a funtzioa
ere hortik hartuko ditu balioak eta arc cos a funtzioa ondorengo
era honetan definituko dugu :
Cos a -1 eta 1 artean kokatuta dagoen moduan, arc cos a funtzioa
ere hortik hartuko ditu balioak eta arc cos a funtzioa ondorengo
era honetan definituko dugu : funtzioa ondorengo era honetan definituko dugu :Aurretik esandakoaren arabera, ondoko hau beteko da :
funtzioa ondorengo era honetan definituko dugu :Aurretik esandakoaren arabera, ondoko hau beteko da :
XXI.3. Tangente funtzioaren alderantzizko funtzioa.
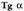 funtzioaren alderantzizko funtzioari
funtzioaren alderantzizko funtzioari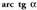 esaten zaio eta arku tangente alfa irakurtzen da. Funtzio hori, aurreko bi kasuetan bezala, tangente funtziotik abiatuta lortzen da lehen koadranteko erdikariarekiko simetria erabiliz.
esaten zaio eta arku tangente alfa irakurtzen da. Funtzio hori, aurreko bi kasuetan bezala, tangente funtziotik abiatuta lortzen da lehen koadranteko erdikariarekiko simetria erabiliz.
Aurreko kasuetan bezalaxe, grafikoak unibokoa izan behar du eta alderantzizko funtzioaren zati posible guztietatik bat hautatu behar da. Normalean,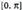 tarteari dagokiona hartu ohi da eta arc cos a funtzioa ondorengo era honetan definituko da :
tarteari dagokiona hartu ohi da eta arc cos a funtzioa ondorengo era honetan definituko da :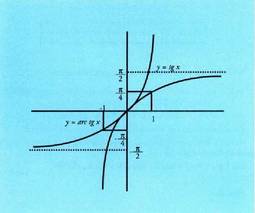 Aurreko grafikoan ikusten denez, ondoko hauek betetzen dira:
Aurreko grafikoan ikusten denez, ondoko hauek betetzen dira:
- Proposatutako ariketak.
12. Koordenatu ardatz berberak erabiliz eta grafiko
bakoitzari kolore desberdina emanez, zirriborra itzazu
ondoko funtzio hauei dagozkienak : 13. Koordenatu ardatz berberak erabiliz eta grafiko
bakoitzari kolore desberdina emanez, zirriborra itzazu
ondoko funtzio hauei dagozkienak :
13. Koordenatu ardatz berberak erabiliz eta grafiko
bakoitzari kolore desberdina emanez, zirriborra itzazu
ondoko funtzio hauei dagozkienak :
XXII. Arrazoi trigonometrikoen batuketa erlazioak.
XXII.1. Bi angeluen batura angeluaren sinua, kosinua eta tangentea.
XXII.I.a. Bi angeluen batura angeluaren sinua.
Bitez a eta b emandako angeluak. Sin (a+b) kalkulatzeko, BCrekiko elkartzuta den AF lerro zuzena marrazten da eta halaber BErekiko elkartzuta den AE ere. Alde elkarzuten artean kokatutako angeluak berdinak direla gogoratuz, EAD angelua ezagutuko dugu eta a angeluaren berdina dela ikusiko.
Aipatutako hiru guneetan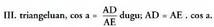 Bestalde, I. triangeluan ondorengoa dago :
Bestalde, I. triangeluan ondorengoa dago : eta
eta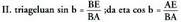 Azken esamolde horiek (1) formulan ordezkatzean, ondoko
hau gelditzen da :
Azken esamolde horiek (1) formulan ordezkatzean, ondoko
hau gelditzen da :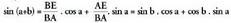 Beraz,
Beraz,
XXII.1.b. Bi angeluen batura-angeluaren kosinua.
Irudian bertan arrazoi daiteke bi angeluen diferentzia edo kendura angeluak zer emango duen.
Bitez a eta b emandako angelu horiek.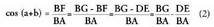 I. triangeluan, zera lortzen da :
I. triangeluan, zera lortzen da : II. triangeluan, zera lortzen da :
II. triangeluan, zera lortzen da :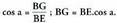 Bestalde, 111. triangeluan, sin a = DE ; DE = AE.sin a
AE
Bestalde, 111. triangeluan, sin a = DE ; DE = AE.sin a
AE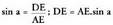 Azken esamolde horiek (2) formulan ordezkatzean, ondoko hau
gelditzen da :
Azken esamolde horiek (2) formulan ordezkatzean, ondoko hau
gelditzen da :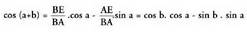 Beraz,
Beraz,
XXII. 1.c. Bi angeluen batura-angeluaren tangentea.
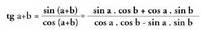 Zenbakitzailea eta izendatzailea cos a. cos b balioaz zatituz,ondorengoa lortzen da :
Zenbakitzailea eta izendatzailea cos a. cos b balioaz zatituz,ondorengoa lortzen da :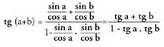 Hau da:
Hau da:
XXII.2. Bi angeluen kendura angeluaren sinua, kosinua eta tangentea.
XXII.2.a. Bi angeluen kendura angeluaren sinua.
Baldin eta bi angeluen batura angeluaren sinuaren formulan b, (- b)-z ordezkatzen bada, ondoko hau lortzen da :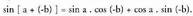 Gauza jakina da
Gauza jakina da Aurreko formulan bidezkoak diren ordezkapenak egiten badira,
ondoko hau lortzen da :
Aurreko formulan bidezkoak diren ordezkapenak egiten badira,
ondoko hau lortzen da :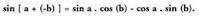 Hau da :
Hau da :
XXII.2.b. Bi angeluen kendura angeluaren sinua.
Baldin eta bi angeluen batura angeluaren kosinuaren formulan b, (- b)-z ordezkatzen bada, ondoko hau lortzen da :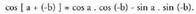 Gauza jakina da
Gauza jakina da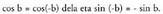 Aurreko formulan bidezkoak diren ordezkapenak egiten badira, ondoko hau lortzen da :
Aurreko formulan bidezkoak diren ordezkapenak egiten badira, ondoko hau lortzen da :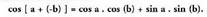 Hau da:
Hau da:
XXII.2.c. Bi angeluen kendura angeluaren tangentea.
Gauza jakina da tg (-b) = - tg b dela. Bi angeluen batura-angeluaren
tangentearen formulan, b, (- b)-z ordezkatzen bada, ondoko
hau lortzen da :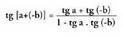 Aurreko formulan bidezkoak diren ordezkapenak egiten badira,
ondorengoa lortzen da :
Aurreko formulan bidezkoak diren ordezkapenak egiten badira,
ondorengoa lortzen da :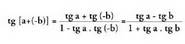 Hau da :
Hau da :
XXII.3. Angelu bikoitzaren sinua, kosinua eta tangentea.
Bi angeluen batura angeluaren sinu, kosinu eta tangentearen formuletan, b, a-z ordezkatzen baldin bada, hau ateratzen da :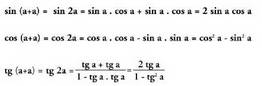 Hau da,
Hau da,
XXII.4. Angelu erdiaren sinua, kosinua eta tangentea.
Aurreko formuletan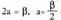 egiten bada, orduan, ondorrengoa ateratzen da:
egiten bada, orduan, ondorrengoa ateratzen da: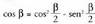 Bestalde, badakigu jakin
Bestalde, badakigu jakin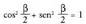 Aurreko bi berdintzak ordenan batzen badira, ondorengoa gelditzen
da:
Aurreko bi berdintzak ordenan batzen badira, ondorengoa gelditzen
da: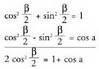 Hortik, zera ateratzen da :
Hortik, zera ateratzen da :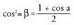 beraz,
beraz,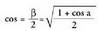 Aurreko bi berdintzen kenketa ordenan eginez gero, honako hau
gelditzen da :
Aurreko bi berdintzen kenketa ordenan eginez gero, honako hau
gelditzen da :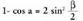 Beraz,
Beraz,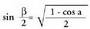 Angelu erdiaren tangentearen balioa, lortutako bi adierazpenetatik
lortzen da :
Angelu erdiaren tangentearen balioa, lortutako bi adierazpenetatik
lortzen da :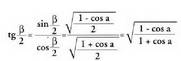 Laburpen-koadroa :
Laburpen-koadroa :
XXIII. Sinuen eta kosinuen batuketa eta kenketa
Formula horiei esker, sinuen eta kosinuen batuketak eta kenketak,
biderkaketa bihur daitezke, eta horrela, logaritmo kalkuluaz
baliatu horiek ebazteko.
XXII.1.a eta XXIL2.a ataletan ikusitakoaren arabera, ondoko
hau dugu :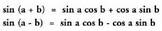 Bi adierazpen horiek elkarren artean batuz eta elkarren artean
kenketa eginez, ondoko hauek lortzen dira :
Bi adierazpen horiek elkarren artean batuz eta elkarren artean
kenketa eginez, ondoko hauek lortzen dira :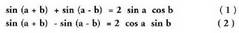 Era berean, gauza jakina da :
Era berean, gauza jakina da : Bi adierazpen horiek elkarren artean batuz eta elkarren artean kenketa eginez, ondoko hau lortzen da :
Bi adierazpen horiek elkarren artean batuz eta elkarren artean kenketa eginez, ondoko hau lortzen da :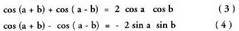 Orain, a + b = A etaa - b = B eginda, honako hau lortzen da:
Orain, a + b = A etaa - b = B eginda, honako hau lortzen da: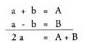 eta hortik,
eta hortik,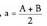 eta
eta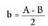 ateratzen dira.
ateratzen dira.
Balio horiek 1, 2, 3 eta 4 formuletan ordezkatuta, ondorengoak lortzen dira : Ebatzitako ariketak.10. Adierazi biderkadura moduan :
Ebatzitako ariketak.10. Adierazi biderkadura moduan :
- Proposatutako ariketak.
14. Ondorengo hauek emanda :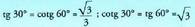 eta
eta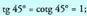 kalkulatu ondoren adierazten diren arrazoien balioak, aurreko ataletan ikusi diren formulak erabiliz :
kalkulatu ondoren adierazten diren arrazoien balioak, aurreko ataletan ikusi diren formulak erabiliz :
XXIV. Identitate trigonometrikoak.
Funtzio goniometrikoen arteko berdintasuna identitatea dela
frogatzeko ezin eman daiteke arau orokorrik. Oro har, eraldaketak,
aurreko puntuetan frogatutako formuletan oinarrituta
egin behar izaten dira, XXII. eta XXV ataletakoetan batez ere.Ebatzitako adibideak.11. Frogatu ondorengo identitatea :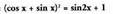 Ebazpena : Ekuazioaren lehen atala, binomio baten karratua da, beraz, honela idatz dezakegu :
Ebazpena : Ekuazioaren lehen atala, binomio baten karratua da, beraz, honela idatz dezakegu :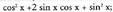 dela gogoratuz eta 2 sin x cos x = sin 2 x dela kontuan hartuta, bigarren atala ateratzen da eta horrenbestez frogatuta gelditzen da identitatea.12. Frogatu ondorengo identitatea :
dela gogoratuz eta 2 sin x cos x = sin 2 x dela kontuan hartuta, bigarren atala ateratzen da eta horrenbestez frogatuta gelditzen da identitatea.12. Frogatu ondorengo identitatea : Ebazpena : Berdintzaren lehen aldeko zenbakitzailea eta izendatzailea
aldatuz gero, ondorengoa ateratzen da :
Ebazpena : Berdintzaren lehen aldeko zenbakitzailea eta izendatzailea
aldatuz gero, ondorengoa ateratzen da :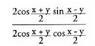 eta hor behar diren sinplifikazioak egin ondoren, honako hau gelditzen
da:
eta hor behar diren sinplifikazioak egin ondoren, honako hau gelditzen
da: Ebazpena: Bigarren atalean faktore komuna ateraz gero, ondorengoa lortzen da :
Ebazpena: Bigarren atalean faktore komuna ateraz gero, ondorengoa lortzen da :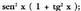 parentesi artean dagoena,
XIII. atalean ikusitakoaren arabera,
parentesi artean dagoena,
XIII. atalean ikusitakoaren arabera,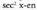 berdina da. Bigarren
aldean orain,
berdina da. Bigarren
aldean orain,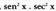 gelditzen da, hots,
gelditzen da, hots,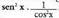 hain zuzen ere, lehen aldeko
hain zuzen ere, lehen aldeko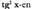
- Proposatutako ariketak.
Frogatu ondorengo identitateak.
XXV Trigonometriako ekuazioak.
Trigonometriako ekuazioak ezezaguna funtzio zirkular baten
argumentu gisa azaltzen dutenak dira. Ezezaguna bakantzean,
gradu edo radianetan adieraz daiteke ezezagunaren balioa.
Ekuazioa ebatzi ondoren, hasierako ekuazioan lortutako emaitzak
egiaztatzea komeni da, izan ere, emaitza arraroak ere ager baitaitezke
.Ebatzitako adibideak.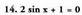 Ebazpena:
Ebazpena: , orduan,
, orduan,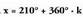 izango da eta baita
izango da eta baita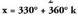 ere.15. Ebatzi
ere.15. Ebatzi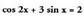 ekuazioa.
Ebazpena:
ekuazioa.
Ebazpena: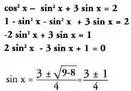 Beraz,
Beraz,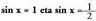 baldin eta sin = 1 bada, x = 90º + 360º K edo
baldin eta sin = 1 bada, x = 90º + 360º K edo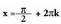 baldin eta
baldin eta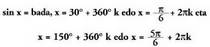 16. Ebatzi ekuazioa hau : tg ( 45° + x) + tg ( 45° + x) = 4
Lehenengo atala garatuz gero, honako hau aurkitzen da :
16. Ebatzi ekuazioa hau : tg ( 45° + x) + tg ( 45° + x) = 4
Lehenengo atala garatuz gero, honako hau aurkitzen da :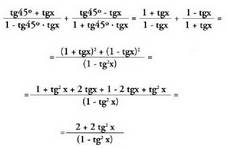 Lehen aldearentzat ateratako adierazpenarekin bigarren aldea berdintzean, honako hau lortzen da :
Lehen aldearentzat ateratako adierazpenarekin bigarren aldea berdintzean, honako hau lortzen da :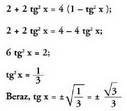 tg x positiboa baldin bada, x = 30° + 360° k izango da edota
agian baita x = 210 ° + 360° k ere.tg x negatiboa bada x = 150° + 360° k izango da edota baita
x = 330° + 360° k ere.17. Ebatzi ondorengo ekuazioa: 4 cos 2x + 3 cos x = 1Ebazpena :
tg x positiboa baldin bada, x = 30° + 360° k izango da edota
agian baita x = 210 ° + 360° k ere.tg x negatiboa bada x = 150° + 360° k izango da edota baita
x = 330° + 360° k ere.17. Ebatzi ondorengo ekuazioa: 4 cos 2x + 3 cos x = 1Ebazpena :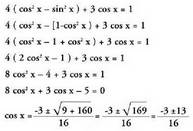 Baldin eta cos x = - 1 bada, x = 180 ° + 360° k izango daBaldin eta
Baldin eta cos x = - 1 bada, x = 180 ° + 360° k izango daBaldin eta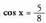
- Proposatutako ariketak.
XXVI. Trigonometriako ekuazioen sistemak
Ekuazio trigonometrikoen sistemak, algebrako ekuazioen printzipio
berberak jarraituz ebazten dira. ordezkapen, berdinketa
edota laburpen sistema erabiliz ebatz daitezke. Ariketa ebatzi aurretik,
metodo horietako onena zein den jakitea komeni izaten da,
izan ere, hautaketa ondo egiteak, eragiketak asko labur baititzake.Ebatzitako ariketak.18. Ebatzi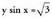 sistema
sistema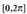 tartean
tartean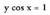 Ebazpena:
Bi ekuazioak atalez atal zatituz gero, hau ateratzen da :
Ebazpena:
Bi ekuazioak atalez atal zatituz gero, hau ateratzen da :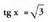 Eta hortik, x = 60° edota baita x = 240° ere.Baldin eta x = 60º bada, y cos x = 1 ekuazioan ordezkatuz, zera lortzen da :
Eta hortik, x = 60° edota baita x = 240° ere.Baldin eta x = 60º bada, y cos x = 1 ekuazioan ordezkatuz, zera lortzen da :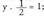 ; eta hortik y = 2.Baldin eta x = 240° bada, ekuazio berean ordezkatuz,
; eta hortik y = 2.Baldin eta x = 240° bada, ekuazio berean ordezkatuz,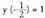 lortzen da eta hortik y = -2.19. Ebatzi sin x - sin y = 1 sistema,
lortzen da eta hortik y = -2.19. Ebatzi sin x - sin y = 1 sistema, tartean sin x + sin y = 1Ebazpena : laburpen metodoa erabilita, honako hau lortzen da : 2 sin x = 2 , hau da, sin x = 1, beraz, x = 90° da.. in x + sin y = 1 ekuazioan ordezkatuz, 1 + sin y = 1 lortzen da eta hortik,
tartean sin x + sin y = 1Ebazpena : laburpen metodoa erabilita, honako hau lortzen da : 2 sin x = 2 , hau da, sin x = 1, beraz, x = 90° da.. in x + sin y = 1 ekuazioan ordezkatuz, 1 + sin y = 1 lortzen da eta hortik,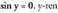 balio posibleak y = 0° eta y = 180° dira.20. Ebatzi
balio posibleak y = 0° eta y = 180° dira.20. Ebatzi sistema,
sistema,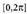 ; tartean sin x + sin y = 1Ebazpena : Sinuen eta kosinuen batuketak aldez aurretik biderkaketa
moduan jarri behar dira.
; tartean sin x + sin y = 1Ebazpena : Sinuen eta kosinuen batuketak aldez aurretik biderkaketa
moduan jarri behar dira.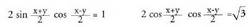 Bi ekuazioak atalez atal zatitzen badira, honako hau lortzen da :
Bi ekuazioak atalez atal zatitzen badira, honako hau lortzen da :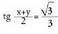 hau da ,
hau da , edota baita
edota baita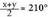 ere.Baldin eta
ere.Baldin eta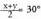 bada, balio hori ekuazioan ordezkatzean, ondorengoa lortuko da:
bada, balio hori ekuazioan ordezkatzean, ondorengoa lortuko da: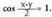 Beraz,
Beraz,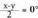
- Proposatutako ariketak.
23. Ebatzi 24. Ebatzi
24. Ebatzi
Ebazpenen zerrenda
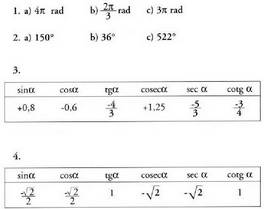 5.a. Baldin eta
5.a. Baldin eta lehenengo koadrantean badago.
lehenengo koadrantean badago. 5.b. Baldin eta a hirugarren koadrantean badago.
5.b. Baldin eta a hirugarren koadrantean badago.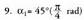 lehenengo koadrantean dago
lehenengo koadrantean dago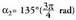 bigaren koadrantean dago
bigaren koadrantean dago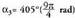 lehenengo koadrantean dago
lehenengo koadrantean dago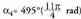 bigarren koadrantean dago10. Bigarren koadrantean.11.
bigarren koadrantean dago10. Bigarren koadrantean.11. 12.
12. 13.
13. 12. eta 13. ariketen ondorioa: aldagai askea "a" konstante batez
biderkatzen bada, periodoa konstante horren balioaz zatituta gelditzen da eta funtzioa "laburtuz" doa "a" handitzen denean.
12. eta 13. ariketen ondorioa: aldagai askea "a" konstante batez
biderkatzen bada, periodoa konstante horren balioaz zatituta gelditzen da eta funtzioa "laburtuz" doa "a" handitzen denean.
Bestela esanda,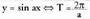 Aldagai askea "b" konstante batez zatitzen bada, periodoa konstante
horren balioaz biderkatuta gelditzen da eta "b" handitzean
funtzioa "luzatuz" doala ikusten da. hau da,
Aldagai askea "b" konstante batez zatitzen bada, periodoa konstante
horren balioaz biderkatuta gelditzen da eta "b" handitzean
funtzioa "luzatuz" doala ikusten da. hau da,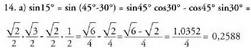 Beste era honetan ere ebatz daiteke:
Beste era honetan ere ebatz daiteke:
Triangeluen ebazpena
I. Sarrera.
Trigonometriaren ikasle zintzoari sor dakiokeen lehenengo galdera
zera da, zergatik aztertu eta ikasi behar dira triangeluak eta ez
beste edozein poligono?. Erantzuna argia eta erabakiorra da.
Triangelua da bere aldeen luzera aldatu gabe ezin deforma daitekeen
poligono bakarra ; beraz, irudi "zurruna" da. Lau aldeko
poligono baten kasuan, koadro baten markoa adibidez, zurrun gelditzea
nahi bada, barra bat jarri beharra dago parez pare dauden bi
erpinak elkartuz eta orduan, bi triangelu lortzen dira. Horrek esan
nahi du laukia, oro har, bi triangelutatik abiatuta azter daitekeela.
Gauza bera gertatzen da pentagonoan ; kasu honetan ordea, hiru
triangelu lortzen dira. Oro har, "n" aldedun poligonoa, "n-2"
triangelutan bana daiteke eta horiek modu zehatzean aztertu eta
ikasi daitezke inolako deformazio ahalbiderik gabe.
Gainera, errepideak, tunelak eta gisakoak eraikitzeko mapa
topografikoak prestatu behar direnean, batez ere eta bereziki,
triangelutze metodoa erabiltzen da. Metodo hori honako honetan
oinarritzen da, alegia, triangelu baten elementu batzuk ezagututa,
haren gainerako elementu guztiak kalkula daitezkeela, hemen
ondoren ikusiko diren teorema eta kalkuluen laguntzarekin.
Triangeluak bi motakoak izan daitezke : triangelu zuzenak edo
angeluzuzenak ez diren triangeluak. Ebazteko modua desberdina
dute eta baita mota bakoitza ebazteko egin beharreko ebazpenen
zailtasuna ere ; bigarren motakoen ebazpena, hots, angeluzuzenak
ez direnena, askoz ere konplexuagoa da.
Triangelua zuzena bada, ondoko hauek jakin behar dira :
• Aldeen arteko erlazioa. Pitagorasen teorema.
• Angeluen arteko erlazioa.
• Aldeen eta angeluen arteko erlazioak.
Triangelua zuzena ez bada, hiru teorema hauek behar dira ebatzi
ahal izateko :
• Sinuen teorema.
• Kosinuaren teorema.
• Tangentearen teorema.
I I. Triangelu zuzena.
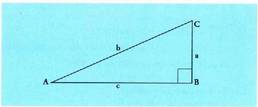 Bedi ABC triangelua ; bertan ezagunak ditugu• Aldeen arteko erlazioa, hots, Pitagorasen teorema, honi aplikatuta, hau gelditzen da :
Bedi ABC triangelua ; bertan ezagunak ditugu• Aldeen arteko erlazioa, hots, Pitagorasen teorema, honi aplikatuta, hau gelditzen da :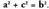 • Angeluen arteko erlazioa : A + B + C = 180°. Angelu baten
balioa ezagutzen bada, bestea berehala kalkulatzen da, izan ere, A
+ C = 90 ° baita.• Aldeen eta angeluen arteko erlazioak, hau da, arrazoi trigonometrikoak,
triangelu honetan ondoko hauek direnak :
• Angeluen arteko erlazioa : A + B + C = 180°. Angelu baten
balioa ezagutzen bada, bestea berehala kalkulatzen da, izan ere, A
+ C = 90 ° baita.• Aldeen eta angeluen arteko erlazioak, hau da, arrazoi trigonometrikoak,
triangelu honetan ondoko hauek direnak :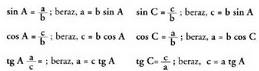
• Lehen kasua:
hipotenusa eta angelu bat ematen dira, angelu hori zorrotza da, izan ere, bai A eta baita C ere 90° baino txikiagoak baitira. Ezezagunak, beste angelua eta katetuak dira.Ebatzitako ariketa.
1. Plano oker batek 45 mko luzera du eta horizontalarekin 30°ko
angelua eratzen du. Kalkulatu beste angelua eta katetuak.Ebazpena:
- Proposatutako ariketa.
1. Errepide zati batean, bere inklinazio edo okertasun angelua neurtu da eta 5°koa da. Kalkulatu beren artean 2,6 Kmko distantzia duten bi herrien artean dagoen desnibela.
• Bigarren kasua:
Katetu bat eta angelu bat ematen dira; angelua zorrotza da, ezen, bai A eta baita C ere, 90° baino txikiagoak baitira. Ezezagunak berriz, beste angelua eta beste katetua izango dira.Ebatzitako ariketa.
2. Egunaren une jakin batean, zuhaitz baten itzala 12 mkoa da
eta zoruak zuhaitz burua eta itzalaren amaierako muturra elkartzen
dituen lerro zuzenarekin duen angelua 50°koa. Kalkulatu zuhaitzaren
altura.Ebazpena
- Proposatutako ariketak.
2. gf = gh = df = dh = he = 1,5 m zuzenkiek eta bd = ih
zuzenkiek 6 mko luzera dutela jakinda, kalkulatu
dorrearen altura.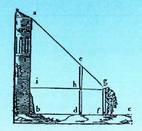 3. En neurtutako angelua 45°koa da eta Yn neurtutakoa
30°koa. E eta Yren arteko distantzia 25 kanakoa da
(kana 1 = 835,9 mm) eta neurtzaileen altura 2 kanakoa
da, zein da dorrearen altura?
3. En neurtutako angelua 45°koa da eta Yn neurtutakoa
30°koa. E eta Yren arteko distantzia 25 kanakoa da
(kana 1 = 835,9 mm) eta neurtzaileen altura 2 kanakoa
da, zein da dorrearen altura?
• Hirugarren kasua :
Hipotenusa eta katetu bat ematen dira, ezezagunak, beste aldea eta bi angeluak dira.Ebatzitako ariketa.3. Konpas baten bi besoek, 12 cm neurtzen dituzte. Punten arteko distantzia 8 cmkoa izan arte ireki dira. Zein izango da bi besoek elkarren artean eratutako angelua?Ebazpena
- Proposatutako ariketa.
4. A eta B ontzien kokaerak, triangelu zuzena eratzen du faro batekin. A ontzia farotik 6 kmra dago eta B berriz 4 kmra. Kalkulatu bi ontzien artean dagoen distantzia.
• Laugarren kasua :
Bi katetu ematen dira. Ezezagunak hipotenusa eta angeluak dira. Pitagorasen teoremaren bitartez edota arrazoi trigonometrikoak erabiliz ebatz daiteke.Ebatzitako ariketa.4. Pertsona bat bere familiakoak agurtzera joan da kaira, eta
itsasontzia irten denean kaian zehar ibiltzen hasi da ontziaren
ibilbidearekiko perpendikularrean. Ontziaren lastertasuna 20
km/h bada eta oinezkoarena 5 km/h; zein distantziara egongo
da ontzia pertsonarengandik ordu erdia igaro ordoren?
Ontziak egindako distantzia : 10 km.Oinezkoak egindako distantzia : 2,5 km.. ien artean izango den tartea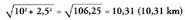 Arrazoi trigonometrikoak erabiliz
Arrazoi trigonometrikoak erabiliz
- Proposatutako ariketa.
5. Lurrartzera doan hegazkin baten eta bere lorategian eguzkia hartzen ari den behatzaile baten arteko distantzia 2 kmkoa da, lurzoruarekiko elkarzut neurtuta . Behatzailearen etxea aireportutik 5,6 kmra baldin badago, zein izango da hegazkinak lurreratzen hasi zenetik egindako distantzia lerro zuzenean joan bada? Zein da jaisten hasi zeneko norabidearen angelua? Eta hegazkinaren ibilbideak aireportuko lurzoruarekin eratzen duen angelua?
I I I. Sinuen teorema.
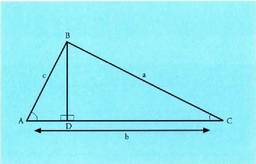 Bedi ABC triangelua eta bertan BD zuta marraztu zaio AC
katetuari. Era horretan, bi triangelu zuzen lortu dira : ADB eta
BDC. BD altura da bi triangeluetan. Bi triangelu horietan, ondoko
hauek ditugu :
Bedi ABC triangelua eta bertan BD zuta marraztu zaio AC
katetuari. Era horretan, bi triangelu zuzen lortu dira : ADB eta
BDC. BD altura da bi triangeluetan. Bi triangelu horietan, ondoko
hauek ditugu :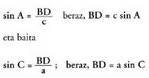 Ikusten denez, aurreko adierazpenetako lehen atalak berdinak
dira eta hortik ondorioztatzen denez, bigarren atalek ere berdinak
izan behar dute. Horren arabera, ondorengoa idatz daiteke :c sin A = a sin C, edota beste era batera idatzita :
Ikusten denez, aurreko adierazpenetako lehen atalak berdinak
dira eta hortik ondorioztatzen denez, bigarren atalek ere berdinak
izan behar dute. Horren arabera, ondorengoa idatz daiteke :c sin A = a sin C, edota beste era batera idatzita :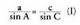 Era berean, A erpinetik BC katetuari perpendikularra marrazten
bazaio, AD da triangeluaren altura.
Era berean, A erpinetik BC katetuari perpendikularra marrazten
bazaio, AD da triangeluaren altura.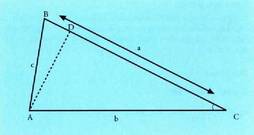 Kasu horretan, ondorengoa daukagu :
Kasu horretan, ondorengoa daukagu :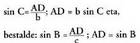 Bigarren aldeak berdinduz, ondoko hau lortzen da :
Bigarren aldeak berdinduz, ondoko hau lortzen da :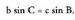 , eta proportzio moduan idatzita,
, eta proportzio moduan idatzita,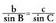 Azken adierazpen hori Iean ordezkatuta, sinuen teorema adierazten
duen formulara iristen da :
Azken adierazpen hori Iean ordezkatuta, sinuen teorema adierazten
duen formulara iristen da : eta ondorengo era honetan enuntzia daiteke :Sinuen teorema : Triangelu baten aldeak horien
aurrez aurreko angeluen sinuen proportzionalak dira.ABC triangeluak angelu kamutsa baldin badu, C adibidez,
kontuan hartu behar da C eta 180 0 - C angelu betegarriek sinu
berdina dutela, XVII.2. atalean ikusi denez.
eta ondorengo era honetan enuntzia daiteke :Sinuen teorema : Triangelu baten aldeak horien
aurrez aurreko angeluen sinuen proportzionalak dira.ABC triangeluak angelu kamutsa baldin badu, C adibidez,
kontuan hartu behar da C eta 180 0 - C angelu betegarriek sinu
berdina dutela, XVII.2. atalean ikusi denez.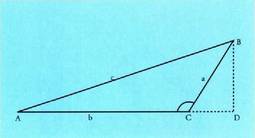 Kasu honetan,
Kasu honetan,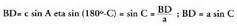 Bi adierazpen horien bigarren atalak berriro berdinduz, hau ateratzen
da :
Bi adierazpen horien bigarren atalak berriro berdinduz, hau ateratzen
da :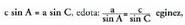
IV. Kosinuaren teorema.
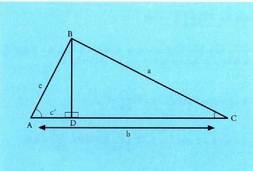 Bedi ABC triangelua eta bertan, AC katetuari BD perpendikularra
marraztu zaio, era horretara ADB eta BDC triangelu
zuzenak lortuz.Bedi
Bedi ABC triangelua eta bertan, AC katetuari BD perpendikularra
marraztu zaio, era horretara ADB eta BDC triangelu
zuzenak lortuz.Bedi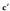 , c katetuak AC aldean duen proiekzioa ; bere balioa, honako formula honek emana dator :
, c katetuak AC aldean duen proiekzioa ; bere balioa, honako formula honek emana dator :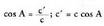 ADB triangeluan Pitagorasen teorema aplikatzean, honako hau ateratzen da :
ADB triangeluan Pitagorasen teorema aplikatzean, honako hau ateratzen da :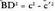 BDC triangeluan gauza bera egiten baldin bada, beste hau lortzen da :
BDC triangeluan gauza bera egiten baldin bada, beste hau lortzen da :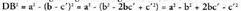 Ikusten denez, aurreko adierazpenaren lehen atalak, berdinak
dira eta hortik ondorioztatzen da, alegia, bigarren atalak ere hala
direla. Orduan, era honetara idatz daiteke :
Ikusten denez, aurreko adierazpenaren lehen atalak, berdinak
dira eta hortik ondorioztatzen da, alegia, bigarren atalak ere hala
direla. Orduan, era honetara idatz daiteke :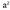 askatuz eta
askatuz eta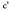 ordezkatuz, honako hau ateratzen da :
ordezkatuz, honako hau ateratzen da :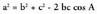 C angeluari aplikatu izan balitzaio,
C angeluari aplikatu izan balitzaio,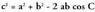 lortuko zatekeen.b aldearen kasuan, honako emaitza honetara iristen da :
lortuko zatekeen.b aldearen kasuan, honako emaitza honetara iristen da :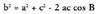
V. Tangentearen teorema.
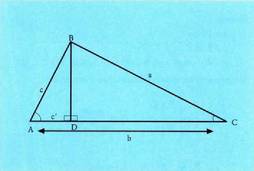 Proportzioen ezaugarrietako batek dioenez, aurrekarien batura
atzekarien baturaz zatituta, edozein arrazoiaren berdina da.
Proportzioen ezaugarrietako batek dioenez, aurrekarien batura
atzekarien baturaz zatituta, edozein arrazoiaren berdina da.
ABC triangeluan propietate hori sinuaren teoremarekin erabiltzen
bada, ondoko berdintza hauek idatz daitezke :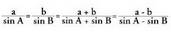 edo baita,
edo baita,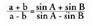 Kasu honetan XXIII. atalean ikusitakoa aplikatuz, sinuen batuketa
edota kenketa biderkadura bihur daitekeelako formula aplikatuz
alegia, hau lortzen da :
Kasu honetan XXIII. atalean ikusitakoa aplikatuz, sinuen batuketa
edota kenketa biderkadura bihur daitekeelako formula aplikatuz
alegia, hau lortzen da :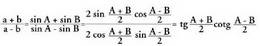 hau da :
hau da :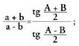 emaitza hau ikusita, tangentearen teorema era honetan adieraz daiteke
:Tangentearen teorema : Edozein triangelutan, aldeen
batura zati aldeen kenduraren balioa aurrez aurreko
angeluen baturaerdiaren tangentea, zati angelu
berberaren kenduraerdiaren tangenteak
ematen duen balioaren berdina da.Ariketa ebatzia.
emaitza hau ikusita, tangentearen teorema era honetan adieraz daiteke
:Tangentearen teorema : Edozein triangelutan, aldeen
batura zati aldeen kenduraren balioa aurrez aurreko
angeluen baturaerdiaren tangentea, zati angelu
berberaren kenduraerdiaren tangenteak
ematen duen balioaren berdina da.Ariketa ebatzia.
5. Triangelu batean, katetu batek 7 cm ditu, besteak 10 cm
eta beren arteko angeluak 60° balio du. Kalkulatu beste katetua
eta beste bi angeluen balioak.Ebazpena :Datuak : b = 10 cm c = 7 cm A = 60 ° ; Baldin eta A = 60° bada, orduan, B + C = 120 ° Tangentearen teorema erabiltzean, hau ateratzen da : ondorengo sistema ebatzita :
ondorengo sistema ebatzita :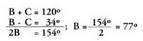 C = 120° - 770 = 43°Angeluen balioak jakinda, aldeak sinuen teorema erabiliz kalkulatzen
dira :
C = 120° - 770 = 43°Angeluen balioak jakinda, aldeak sinuen teorema erabiliz kalkulatzen
dira :
V. Briggsen formulak.
Formula hauek, aldeak ezagunak izanda triangeluen angeluak
kalkulatzeko balio dute.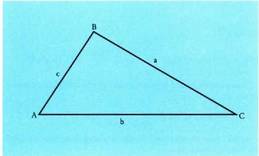 Kosinuaren teorema aZ = b2 + c 2 - 2 b c cos A izanda, A angeluaren
kosinua bakandu eta ondorengoa gelditzen da :
Kosinuaren teorema aZ = b2 + c 2 - 2 b c cos A izanda, A angeluaren
kosinua bakandu eta ondorengoa gelditzen da :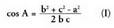 Bero balio hori XXII.4 atalean ateratako
Bero balio hori XXII.4 atalean ateratako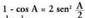 erlazioan ordezkatzen bada, beste hau geldituko da :
erlazioan ordezkatzen bada, beste hau geldituko da :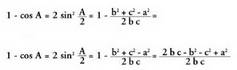 Bigarren ataleko zenbakitzailea karratu diferentzia gisa idatz daiteke :
Bigarren ataleko zenbakitzailea karratu diferentzia gisa idatz daiteke :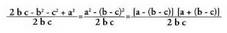 eta azkenean, hauxe lortzen da :
eta azkenean, hauxe lortzen da :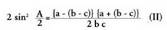 XXII.4. atalean lortutako
XXII.4. atalean lortutako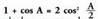 erlazioarekin modu berean lan eginda honako hau ateratzen da :
erlazioarekin modu berean lan eginda honako hau ateratzen da :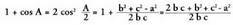 Bigarren aldeko zenbakitzailea, karratu diferentzia moduan idatz
daiteke, beraz, azken emaitza honako hau izango da :
Bigarren aldeko zenbakitzailea, karratu diferentzia moduan idatz
daiteke, beraz, azken emaitza honako hau izango da :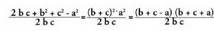 hau da,
hau da,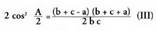 Triangeluaren perimetro erdiari "p" esanez gero, hau lortzen
da: a+ b + c = 2 p.Azkeneko berdintza honi 2a, 2b eta 2c hurrenez hurren kenduta,beste
hau ateratzen da a+ b+ c- 2 a = 2 p- 2 a= 2( p -a)
Triangeluaren perimetro erdiari "p" esanez gero, hau lortzen
da: a+ b + c = 2 p.Azkeneko berdintza honi 2a, 2b eta 2c hurrenez hurren kenduta,beste
hau ateratzen da a+ b+ c- 2 a = 2 p- 2 a= 2( p -a)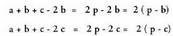 Aurreko 11. eta 111. erlazioetan adierazpen berri hauek sartuz
gero, hau lortzen da :
Aurreko 11. eta 111. erlazioetan adierazpen berri hauek sartuz
gero, hau lortzen da :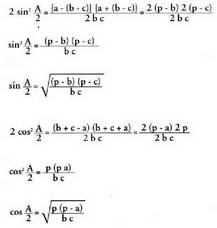 Sinutik eta kosinutik abiatuta,
Sinutik eta kosinutik abiatuta,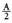 angeluaren tangentea lortzen da :
angeluaren tangentea lortzen da :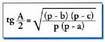 Era berean,
Era berean,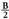 eta
eta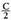 angeluen tangenteak lortzen dira :
angeluen tangenteak lortzen dira :
VI. Triangeluaren azalera kalkulatzeko formulak.
Triangeluaren azalera kalkulatzeko metodoa, eskura ditugun datuen araberakoa da. Ondoren, gerta daitezkeen kasuen berri ematen da.
VI. 1. Lehenengo kasua. Datuak: Alde bat eta alde horri dagokion altura.
Goiko triangeluan, oinarria "b" aldea da, eta altura aurrez aurreko erpinetik hari marraztutako zuta, hots, "h". Datu horiekin, gauza jakina da triangeluaren azalera, ondoko formula honek emana datorrela :
VI. 2. Bigarren kasua. Datuak: Bi alde eta beren arteko angelua.
Irudiko triangeluan, "b" eta "c" aldeak eta A angelua dira ezagunak
. Badakigu jakin, sin A= h ; beraz, h = c sin A. I. formulan
ordezkatuta, triangeluaren azalera lortzen da :
VI. 3.Hirugarren kasua. Datuak : Alde bat eta bi angelu
Irudiko triangeluan, adibidez, "a" aldea eta A eta C angeluak ezagutzen dira.B angelua kalkulatzen da 180°ko balioari A eta C angeluen balioa kenduta. B = 180 0 - ( A + C) eta XVII.2 atalean ikusia denez, sin B = sin (A + C).Sinuen teorema erabiliz, "b" kalkulatzen da :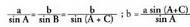 Bestalde,
Bestalde,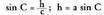 I. formulan ordezkatuz, honako hau ateratzen da :
I. formulan ordezkatuz, honako hau ateratzen da :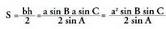 Baina XVII.2 ataletik badakigu, sin A = sin (B+C) dela, beraz, azken ordezkapen bat eginez, trianguluaren azalera ematen duen formulara iristen da.
Baina XVII.2 ataletik badakigu, sin A = sin (B+C) dela, beraz, azken ordezkapen bat eginez, trianguluaren azalera ematen duen formulara iristen da.
VI.4. Laugarren kasua. Datuak : Bi alde eta zirkunferentzia zirkunskribatuaren erradioa.
R zirkunferentzia zirkunskribatuaren erradioa izanda eta sinuen teoremaren interpretazio geometrikoak honako hau idazteko bide ematen duela jakinda :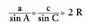 eta gainera,
eta gainera,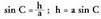 denez,azaleraren formulan ordezkatzean, beste hau gelditzen da :
denez,azaleraren formulan ordezkatzean, beste hau gelditzen da :
VI.5. Bosgarren kasua. Datuak : Perimetroa eta zirkunferentzia inskribatuaren erradioa.
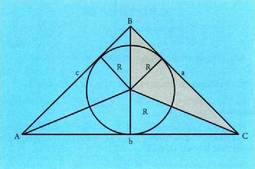 Goiko irudian azaltzen denez, triangelua beste hirutan zatituta
gelditzen da eta horietan R inskribatutako zirkunferentziaren erradioa,
triangelu horien altura da eta horien oinarriak triangelu
nagusiaren aldeak dira.Horrek, honako hau idazteko aukera ematen du :
Goiko irudian azaltzen denez, triangelua beste hirutan zatituta
gelditzen da eta horietan R inskribatutako zirkunferentziaren erradioa,
triangelu horien altura da eta horien oinarriak triangelu
nagusiaren aldeak dira.Horrek, honako hau idazteko aukera ematen du :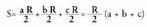 V puntuan ikusi den moduan, a+b+c = 2 p da, beraz, azken formula honela gelditzen da :
V puntuan ikusi den moduan, a+b+c = 2 p da, beraz, azken formula honela gelditzen da :
VI.6. Seigarren kasua. Datuak: Hiru alde.
HERON-EN FORMULA.
VI. atalaren triangeluan, gauza jakina da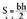 dela eta
dela eta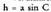 izanik, azken adierazpen hau lehenengoan ordezkatuz, honako hau lortzen da :.
izanik, azken adierazpen hau lehenengoan ordezkatuz, honako hau lortzen da :.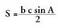 XXII.3. atalean ikusi denez,
XXII.3. atalean ikusi denez,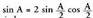 da, eta azaleraren formula honela idatz daiteke:
da, eta azaleraren formula honela idatz daiteke: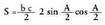 Briggs-en formuletatik, V puntua, gauza jakina da :
Briggs-en formuletatik, V puntua, gauza jakina da :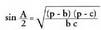 dela
eta
dela
eta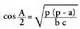 dela
bertan, p perimetro erdia delarik ; horrek beste hau idazteko aukera ematen du :
dela
bertan, p perimetro erdia delarik ; horrek beste hau idazteko aukera ematen du :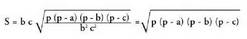 hots, triangeluaren azaleraren azken formula, ondoko hau dela :
hots, triangeluaren azaleraren azken formula, ondoko hau dela :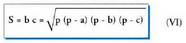 Azken formula hau, Heronen formula da eta oso baliagarria da
hiru aldeak ezagunak direnean.Ebatzitako ariketak6. Kalkulatu triangelu baten azalera bere hiru aldeak ezagunak
direlarik. a = 15 cm; b = 20 cm; eta c = 25 cm.a) Heronen formula erabiltzen bada, ebazpena oso erraza da :
Azken formula hau, Heronen formula da eta oso baliagarria da
hiru aldeak ezagunak direnean.Ebatzitako ariketak6. Kalkulatu triangelu baten azalera bere hiru aldeak ezagunak
direlarik. a = 15 cm; b = 20 cm; eta c = 25 cm.a) Heronen formula erabiltzen bada, ebazpena oso erraza da :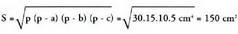 b) Kosinuaren teoremara jotzea nahiago bada, jarraitu beharreko
urratsak hauek izan daitezke :
b) Kosinuaren teoremara jotzea nahiago bada, jarraitu beharreko
urratsak hauek izan daitezke :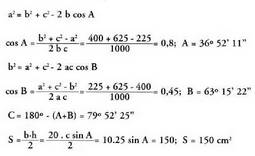 7. Kalkulatu falta den katetua eta beste angeluak ondokotriangeluan. Kalkulatu triangelu horren azalera ere.
7. Kalkulatu falta den katetua eta beste angeluak ondokotriangeluan. Kalkulatu triangelu horren azalera ere. a) Beste katetua kalkulatzeko, kosinuaren teorema erabil daiteke.
a) Beste katetua kalkulatzeko, kosinuaren teorema erabil daiteke.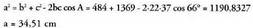 Beste angeluak kalkulatzeko, sinuen teorema erabil daiteke :
Beste angeluak kalkulatzeko, sinuen teorema erabil daiteke :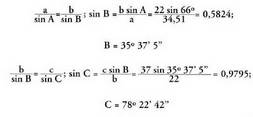 b) Azalera berriz, lortutako datuekin kalkula daiteke :
b. 1 Heronen formularen bidez :
b) Azalera berriz, lortutako datuekin kalkula daiteke :
b. 1 Heronen formularen bidez :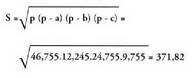 b.2 Sinuaren teoremaren bidez :
b.2 Sinuaren teoremaren bidez :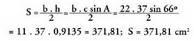 8. Ondoko irudian, DC=300 m distantzia ezaguna da eta ADF =
25°, ACB = 32°, CDF=40°, DCF = 46°. Datu horiekin kalkulatu AB
distantzia.
8. Ondoko irudian, DC=300 m distantzia ezaguna da eta ADF =
25°, ACB = 32°, CDF=40°, DCF = 46°. Datu horiekin kalkulatu AB
distantzia.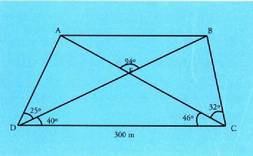 DFC triangeluan :DFC angelua = 180° - 86° = 94°
DFC triangeluan :DFC angelua = 180° - 86° = 94°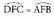 Sinuen teoremaren bitartez, FC eta FD kalkulatzen dira :
Sinuen teoremaren bitartez, FC eta FD kalkulatzen dira :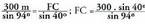 FC = 193,3 m
FC = 193,3 m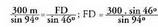 FD = 216,3 mAFD triangeluan, sinuen teoremaren bidez AF kalkulatzen da :
FD = 216,3 mAFD triangeluan, sinuen teoremaren bidez AF kalkulatzen da :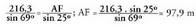 BFC triangeluan, teorema horren berorren bidez BF kalkulatzen da :
BFC triangeluan, teorema horren berorren bidez BF kalkulatzen da :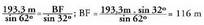 AFB triangeluan, bi katetu eta horien artean eratzen duten angelua
ezagutzen dira. Kosinuaren teoremaren bidez AB kalkulatzen da :
AFB triangeluan, bi katetu eta horien artean eratzen duten angelua
ezagutzen dira. Kosinuaren teoremaren bidez AB kalkulatzen da :
- Proposatutako ariketak
6. Ondoren, sei triangeluetako katetu eta hipotenusa
izan daitezkeen aldeak ematen dira. Esan triangelu
horiek zuzenak diren ala ez. 7. Aurkitu koadroko honetako triangelu zuzenetan falta
diren datuak.
7. Aurkitu koadroko honetako triangelu zuzenetan falta
diren datuak. 8. Kalkulatu koadroko honetako triangeluetan faltadiren datuak.
8. Kalkulatu koadroko honetako triangeluetan faltadiren datuak. 9. Ondoko irudian, AB = 530 m distantzia ezaguna da
eta ABF = 40°, FAB = 30°, FAD = 80°, FBC = 60°.
9. Ondoko irudian, AB = 530 m distantzia ezaguna da
eta ABF = 40°, FAB = 30°, FAD = 80°, FBC = 60°.
Datu horiekin, kalkulatu DC distantzia.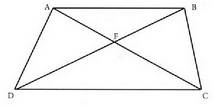 10. Kalkulatu irudi honetako dorrearen altura :
10. Kalkulatu irudi honetako dorrearen altura :
Emaitzen eranskina .
Emaitzen eranskina.1. Desnibela : 226.6 m2. Dorreen altura : 9 m3. Dorrearen altura = AB + B lurzoruarekiko = 34,153 kana +
2 kana = 36,153 kana =30,22 m4.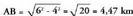 ; ontzien arteko distantzia : 4,47 km.
; ontzien arteko distantzia : 4,47 km.
5. Hegazkinak egindako bidea : 5,95 km.. = 19°39'13" eta b= 70° 20' 47"6. a) EZ b) EZ c) BAI d) BAI e) BAI f) EZ