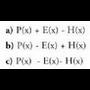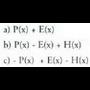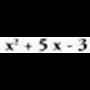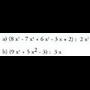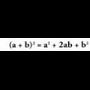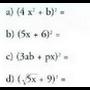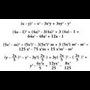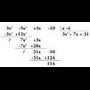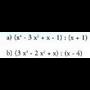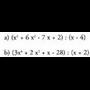Matematika»Aljebra
Aljebra
"jainkoaren laguntza preziatuarekin diot: aljebra artea eta al-mugabalarena zientziazko arte bat da ; zenbaki osoak eta handitasun neurgarriak ditu xede, ezezagun diren heinean, baina hoiek mugatzeko balio dezakeen gauza ezagun batek elkarrekin erlazionatzen dituela" : Omar Khayyam (XII. m.)
Sarrera
Aljebrako lengoaia edo letrazko lengoaia, problema edo buruketaren
planteamendua orokorragoa izan dadin, zenbakiz eta letrez
baliatuz adierazten dena da.• Adibidea:Adierazi, letrak erabiliz, matematika-esaldi hauen azalpenak :• Zenbaki baten karratua 25 da. Emaitza : • Zenbaki baten kuboa 64 da. Emaitza:
• Zenbaki baten kuboa 64 da. Emaitza: • Zenbaki baten karratua gehi beste baten kuboa 17 da. Emaitza :
• Zenbaki baten karratua gehi beste baten kuboa 17 da. Emaitza : • Bi zenbakien karratuen baturaren erro karratua kalkulatzean, bosteko emaitza lortu da. Emaitza :
• Bi zenbakien karratuen baturaren erro karratua kalkulatzean, bosteko emaitza lortu da. Emaitza :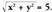
Sarrera
Ondoren datorren gaian, ez da aljebraren ikasketa edo azterketa xeherik
egin nahi. Horren ordez, bidaia txiki bat egin nahi da, eta ahal bada
atsegina, letrak eta zenbakiak nahasten dituen matematikaren adar honetan
zehar.Aljebraren aita, askorentzat, DIOFANTO da, gure kristau aroko III.. endeko greziarra. Hartaz bere lanaren berri baino ez dugu eta hori ere,
arabiarrei esker, izan ere, harenak gorde eta gero latinera itzuli baitzituzten
XVI. mendean. Une hartan, hastear zen aljebraren aurrerakadarentzat
argibide izan zen.Harenak dira "Diofantoren ekuazioak" edota "ekuazio diofantiarrak',
ziur aski ezezagunak Musulmandar Inperioaren garairik handienean, hau
da, VIII. mendearen bigarren erdian eta eta IX.aren lehen erdian, bizi
izan zen AL-KHWARIZMI arabiar matematikariarentzat, hain zuzen ere,
Bagdad bere "Jakinduriaren Etxea" zela bide matematikako garapenaren
munduko ikasgurik garrantzitsuen bilakatu zenean. Garai hartan, Siria,
Iran eta Mesopotamiako jakintsuek, kulturaren babesle handi ziren AL--
MANSUR, HAROUM AL RACHID eta AL-MAMUN hiru kalifen
kalifa aldietan, Euklides, Aristoteles, Ptolomeo eta beste askoren lanak
itzuli zituzten arabierara.AL-MAMUN izan zen IZMI arabiar matematikariarentzat, hain
zuzen ere, Bagdad bere "Jakinduriaren Etxea" sortu zuena eta han AL-
-KHWARIZMIk, inolako zalantzarik gabe, arabiarrek Sinhind izenez
ezagutu zuten astronomia eta matematika lana ezagutu zuen, hain zuzen
ere, indiarren (hinduen) Brahmasphuta Siddhanta edota Surya Siddhanta
izan zitekeena.AL-KHWARIZMIk bi liburu idatzi zituen. Haietako batean, latinezko
itzulpena baizik gordetzen ez denean, indiarren (hinduen) zenbaketa-sistemaren
azalpen hain osoa egin zuen, ezen, agian hori izan baitaiteke gure zenbaketa
sistema arabiar jatorrikoa delako uste zabal bezain faltsuaren jatorria.Beste liburuak, Ilm-al jabr-wa'l-muga-balak izenekoak, aljabr terminoa
du izenburuan, hain zuzen ere, Diofantok hasitako matematika adarrari
izena eman ziona eta une honetan guk esku artean duguna : Aljebra.
Liburu horren edukia, geroago europarrek aljebra ikasteko erabilitakoa,
hurbilago dago egungo aljebra hastapen modernotik, Diofantoren edota
Brahmaguptaren lanetatik baino, izan ere, ekuazioen, bereziki bigarren
mailakoen, zuzeneko eta oinarrizko mailako ebazpenaz baitihardu.Hirugarren mailako ekuazioen ebazpenerako, jauzi handia egin behar
dugu denboran zehar, Errenazimendua arte, XVI. mendea arte, hain
zuzen ere, orduan ikasi eta aztertu baitziren berriro greziar, arabiar eta
indiar matematikari handien lan sakonak Toledon, Itzultzaileen
Eskolaren bitartez egindako itzulpenez baliatuz. Ekuazio kubikoen edota
hirugarren mailakoen ebazpen prozedura orokorra asmatzen lehendabizikoa,
TARTAGLIA (Niccolo Fontana) izan zen. Ziur aski, bere aurkikuntza
Girolamo CARDANOri aipatu bide zion, eta honek, berea balitz
bezala argitaratu zuen, aldez aurretik isilpean gordeko zuela agindua zion
arren. Gertaera horrek argi eta garbi frogatzen du Zientzia bera ere ez
dagoela libre besteren lanak berenak balira bezala aurkezten dituzten
maltzur eta iruzurgileetatik.Tartaglia eta Cardano beren ekuazioak eta kontuak ebazten ari ziren
garai berean, Franciscus VIETA frantziarrak, lan handia egin zuen aljebraz
eta lehenengo aldiz letrak erabili zituen aljebrako ekuazioetan ezezagunak
eta konstanteak izendatzeko. Aurrekoaren aberkide zen Rene
DESCARTESek berriz, ekuazioen irudikapen eta ebazpen grafikoa koordenatu
kartesiarrez egiteko modua aurkitu zuen eta geroak, haren ohoretan,
bere izena eman die koordenatu horiei. Era horretan, Aljebra,
Geometriarako ere erabiltzen hasi zen.Aurrez esandakoei, Aljebraren garapenean eskuhartu zuten hainbat eta
hainbat izenez osatutako zerrenda amaiezina erants dakieke. Horien artean
aipatzekoa da Lucca PACIOLI, 1494an inprimatutako lehenengo aljebra
liburuaren egilea ; Carl Friedrich GAUSS, XIX. mendeko matematikarien
printze deitua eta Aljebrako funtsezko teoremaren frogapena zor
zaiona ; teorema horren arabera, enegarren mailako ekuazio orok, "n" erro
edo ebazpen ditu ; Evariste GALOIS...Ez daude diren guztiak, baina aipamen labur honetan azaltzen direnak
goi mailako matematikari bikainak izan ziren : Horiei zor dizkiegu determinante
eta matrizeen bitartez aljebrako ekuazio sistemak dotore aurkeztu
eta ebazteko moduan bat egin duten bide desberdin eta luzeak ibiltzeko
emandako urratsak.
I.1 Aljebrako adierazpenak.
Aljebrako adierazpena zera da, beren artean aljebrako eragiketa
bidez elkarlotutako letra eta zenbakien multzoa. Eragiketak,
honako hauetakoak izan daitezke : batuketa, kenketa, biderkaketa,
zatiketa, berreketa eta erroketa.• Adibideak : 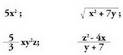
I 1.1. Aljebrako adierazpen motak :
Aljebrako adierazpen batek errokizunean letrarik ez duenean
eta ezein letrak ere zatikia den berretzailerik ez duenean, nazionala
dela esaten da.• Adibideak : Aljebrako adierazpen razional bat osoa da baldin eta izendatzailean,
zenbakitzailean eragina izango duen letrarik edota berretzaile
negatiborik ez badu.• Adibideak:
Aljebrako adierazpen razional bat osoa da baldin eta izendatzailean,
zenbakitzailean eragina izango duen letrarik edota berretzaile
negatiborik ez badu.• Adibideak: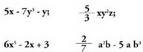 Aljebrako adierazpen razional bat zatikia da baldin eta izendatzailean
letrak baditu edota zenbakitzailean berretzaile negatiboa
baldin badu.• Adibideak :
Aljebrako adierazpen razional bat zatikia da baldin eta izendatzailean
letrak baditu edota zenbakitzailean berretzaile negatiboa
baldin badu.• Adibideak : Aljebrako adierazpen bat, letrak erro zeinupean dituenean edota
letraren batek berretzaile zatikia duenean, irrazionala da.• Adibideak:
Aljebrako adierazpen bat, letrak erro zeinupean dituenean edota
letraren batek berretzaile zatikia duenean, irrazionala da.• Adibideak: 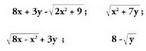
- Ariketak
1. Sailkatu aljebrako adierazpen hauek : 
I.1.2. Aljebrako adierazpenaren zenbakizko balioa.
Bere letrek izan dezaketen balio multzo batentzako, aljebrako
adierazpenaren zenbakizko balioa, letra bakoitza bere balioz
ordezkatu eta aljebrako adierazpenean adierazita dauden eragiketak
egin ondoren ateratzen den zenbakia da. Hau da, aljebrako
adierazpen baten zenbakizko balioa, ezezagun edo letrei
ematen zaien balioaren baitakoa izango da.Ebatzitako Ariketak.1. Kalkulatu adierazpen hauen zenbakizko balioak :
a)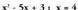 denean;
Emaitza:
denean;
Emaitza: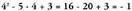 b)
b)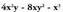 ; x = -1 eta y = 5 direnean ;Emaitza:
; x = -1 eta y = 5 direnean ;Emaitza: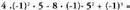
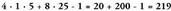 Dituzten letrei edozein balio multzo baina bi adierazpenentzat
ere berbera emanik, zenbakizko balio berbera duten adierazpenei
adierazpen baliokide deitzen zaie.• Adibideak :
Dituzten letrei edozein balio multzo baina bi adierazpenentzat
ere berbera emanik, zenbakizko balio berbera duten adierazpenei
adierazpen baliokide deitzen zaie.• Adibideak :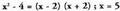 denean ;Emaitza: 21 = 21.
denean ;Emaitza: 21 = 21.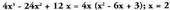
0 Proposatutako ariketak.
2. Kalkulatu adierazpen hauen zenbakizko balioak :
a) direnean ;
b)
direnean ;
b)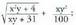
1.2. Monomioak.
Monomioa aljebra adierazpen bat da, letrak eta zenbakiak aljebra
eragiketen mende dituena, batuketaren eta kenketaren mende izan
ezik.• Adibideak : 
1.2.1. Monomioaren koefizientea
Letrekin batera doan zenbakia da. Aurreko adibideetan hauek
dira koefizienteak : Koefizientea idatzi gabe ere egon daiteke ; hala,
Koefizientea idatzi gabe ere egon daiteke ; hala,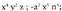
1.2.2. Monomioaren letrazko zatia.
Monomio horretako letra multzoa da. Aurreko adibideetan
hauek dira letrazko zatiak : 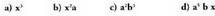
1.2.3. Monomioaren maila
Letrazko zatia osatzen duten letren berretzaileen batura da.Aurreko adibideetan hauek dira graduak : Letrazko zatirik ez badago eta koefizientea zero ez bada, monomio horren maila zero da, eta monomio horri monomio jarraitua esaten zaio.• Adibideak :
Letrazko zatirik ez badago eta koefizientea zero ez bada, monomio horren maila zero da, eta monomio horri monomio jarraitua esaten zaio.• Adibideak :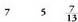
1.2.4. Monomio batek letra bati buruz duen maila
ELetra horrek monomio horretan duen berretzailea da.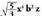
1.2.5. Antzeko monomioak
Letrazko zati berbera dutenak dira• Adibideak : 
I I Monomioekin egiten diren eragiketak.
II.1. Antzeko monomioen aljebra batuketa.
Monomioen batuketa edo kenketa egiteko, monomio
horiek antzekoak izan behar dute.
Monomioen batuketa egiteko, monomio horien koefizientearen
batuketa egin behar da eta letrazko zati berbera
uzten da.
Monomioen kenketa egiteko, koefizientearen kenketa
egiten da eta letrazko zati berbera uzten da.Ebatzitako ariketak.
2. Egin batuketa hauek : a)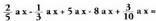 b)
b)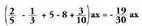
- Proposatutako ariketak
3. Egitzazu batuketa hauek : a) b)
b)
I I.2 Monomio biderkaketak.
Hainbat monomioren biderkaketa, beste monomio bat da :Emaitza monomio horren koefizientea, biderkatutako
monomioen koefizienteen biderkaketa da.Letrazko zatia, monomioetan dauden letren multzoak
osatuta dago eta beren berretzaileak, biderkakizun
bakoitzean letrek dituzten berretzaileen batura dira.Biderkaketaren maila, biderkakizunen mailen batura da.Ebatzitako ariketa.3. Egitzazu biderkaketa hauek.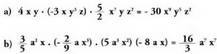
0 Proposatutako ariketak
4. Egitzazu biderkaketa hauek : 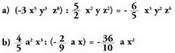
I I.3. Bi monomioren arteko zatiketa.
Bi monomio emanik, zatikizuna bata eta zatitzailea bestea, bien
arteko zatiketa egiteko, monomio zatitzailea ezin daiteke zero
izan eta bere maila, zatikizunarena baino txikiagoa izan behar
du edota gehienera ere zatikizunaren berdina.Bi monomioen arteko zatiketak beste monomio bat ematen
du :Emaitza monomioaren koefizientea, zatikizunaren
eta zatitzailearen koefizienteen arteko zatiketa da.• Letrazko zatia, zatikizun eta zatitzaile diren monomioetako
letren multzoaz osatuta dago. Letra bakoitzak,
berretzailea du eta berretzaile horren balioa, zatikizunean
eta zatitzailean letra horrek dituen berretzaileen
arteko diferentzia da.• Zatiketaren maila, zatikizunaren eta zatitzailearen mailen
arteko diferentzia da.Ebatzitako ariketa.4. Egitzazu zatiketa hauek: 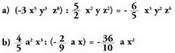
- Proposatutako ariketak
5. Egitzazu zatiketa hauek : 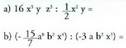
I I.4. Monomio baten berredura.
Monomio baten berredura beste monomio bat da :Berredura monomioaren koefizientea, monomioaren
koefizientearen berredura eginez lortzen da.Letrazko zatia, letra bakoitzaren berretzaileak berreketako
berretzailearekin biderkatuz lortzen dira.Orokorki,Ebatzitako ariketak : 5. Egitzazu berreketa hauek :
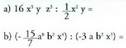
- Proposatutako ariketak
6. Egitzazu berreketa hauek : 
I I I. Polinomioak.
I I I.1. Polinomio funtzioa.
Hainbat monomio funtzioen batuketa den funtzio orori, polinomio-funtzio
deritzo.• Adibidea: Orokorki, polinomio funtzio deitzen zaio R multzoan definituta dagoen
Orokorki, polinomio funtzio deitzen zaio R multzoan definituta dagoen funtzio orori, beti ere ondoko hau idatz daitekeela :
funtzio orori, beti ere ondoko hau idatz daitekeela :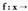
 ; bertan
; bertan , zenbaki errealak direlarik eta n zenbaki arrunta.Bedi polinomio funtzio hau :
, zenbaki errealak direlarik eta n zenbaki arrunta.Bedi polinomio funtzio hau :
I I I.2. Polinomioa.
Polinomioa, hainbat monomioren aljebrako batuketa da.
Monomio bakoitza, polinomioaren gai bat da.• Adibideak: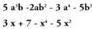
I I I.3. Polinomioaren laburketa.
Bedi polinomio hau :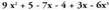 Lehendabizi, elkarren antzeko gaiak taldeka biltzen dira eta talde bakoitzari dagokion monomio baliokideaz ordezkatzen dira.
Lehendabizi, elkarren antzeko gaiak taldeka biltzen dira eta talde bakoitzari dagokion monomio baliokideaz ordezkatzen dira.
Orduan, hau ateratzen da :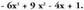
I I I.4. Polinomioaren maila.
Polinomio laburtuak letra batekiko (edota hainbat letrarekiko)
duen maila, letra horren arloan (edo horien arloan) duen mailarik
handieneko gaiak (gaiek) adierazten duena (dutena) da.• Adibideak :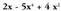 laugarren mailakoa da x-ekiko.
laugarren mailakoa da x-ekiko.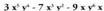
I I I.5. Polinomio berdinak.
Bi polinomio, hutsalak ez direnak, berdinak dira eta orduan bakarrik dira berdinak, baldin eta maila berbera badute eta maila bereko gaien koefizienteak ere berdinak badituzte.
I I I.6. Polinomio homogenoak.
Polinomio homogenoak, gai guztiak maila berekoak dituztenak
dira.• Adibidez: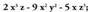
I I I.7. Polinomio ordenatuak.
Polinomio ordenatuak letren berretzaileak gorako edota beherako
ordenan dituztenak dira.• Adibideak :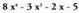 ; Polinomio honetan ordena beherakoa da.
; Polinomio honetan ordena beherakoa da.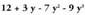
I I I.8. Polinomio osoa.
Polinomio osoa zera da, mailarik handienekotik zero mailako gai askera bitartean, maila bakoitzarentzako gai bat duena.
I I I.9. Polinomio ezosoa.
Mailaren batean edo gehiagotan gaia falta duena da.• Adibideak :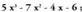 ; hirugarren mailako polinomio osoa da.
; hirugarren mailako polinomio osoa da.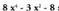 ; laugarren mailako polinomio ezosoa da eta beste modu honetan ere idatz daiteke :
; laugarren mailako polinomio ezosoa da eta beste modu honetan ere idatz daiteke :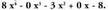 Aldagai bat baino gehiago dituen polinomioa, aldagai horietako
batekiko ordena daiteke. Horrela bada :
Aldagai bat baino gehiago dituen polinomioa, aldagai horietako
batekiko ordena daiteke. Horrela bada : ; x-en berredurak beherako ordenan ordenatuta ditu.
; x-en berredurak beherako ordenan ordenatuta ditu.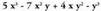
I I I. 10. Polinomioko koefizienteen zerrenda ordenatua.
Polinomioaren idazkera era orokorrean eginda eta
era orokorrean eginda eta duela, bakarra da. Idazkera hori, polinomioarenitxura garatu, laburtu eta ordenatua da, x-en berredurak beherako ordenan dituela.Bitez polinomio hauek :
duela, bakarra da. Idazkera hori, polinomioarenitxura garatu, laburtu eta ordenatua da, x-en berredurak beherako ordenan dituela.Bitez polinomio hauek :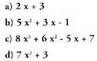
I I I.11. Polinomioen adierazpen edo idazkera laburtua.
Erabilitako ezezaguna x dela emanda, polinomioa zehaztuta gelditzen
da bere koefizienteen zerrenda ordenatua ezagututa.• Adibidea :(15,10,0,-5,8) laugarren mailako polinomio bati dagokio.
Gainera, zeroak, bigarren mailako gairik ez
dagoela adierazten du.
I V. Eragiketak polinomioekin.
IV 1. Polinomioen batuketa.
Polinomioak batzeko, komenigarria da hala behar bada ordenatu
eta osatzea. Gero, zutabe moduan idatzi behar dira, kidekoak
diren maila bereko gaiak bertikalki bat etorraraziz.Ebatzitako ariketak.6. Bitez polinomio hauek : Egin eragiketa hauek :
Egin eragiketa hauek :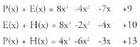
IV 2. Aurkako polinomioak edo simetrikoak.
Bi polinomioren batura zero polinomioa denean, polinomio
horiek aro -kakoak dira.Bedi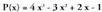 polinomioa eta bedi halaber bere aurkakoa
polinomioa eta bedi halaber bere aurkakoa ere. Beren batuketa egitean,
ere. Beren batuketa egitean,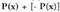
IV.3. Bi polinomioen arteko diferentzia.
P(x) - E(x) polinomioen diferentzia kalkulatzeko, lehenengoari
bigarrenaren aurkakoa edo simetrikoa batzen zaio.Ebatzitako ariketa.7. Bitez polinomio hauek : Egitzazu eragiketa hauek :
Egitzazu eragiketa hauek :
IV 4. Polinomioen aljebrako batuketa.
Hainbat polinomioren batuketa batera egiteko, eragiketa hauek
egin behar dira :1. Polinomioak ordenatu, gorako ordenan edo beherakoan.2. Kideko gaiak batzuek besteen parean ipini bertikalki zutabea
osatuz.3. Kideko gaien batuketa eragiketak egin.Ebatzitako ariketa.8. Bitez polinomio hauek :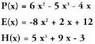 Egitzazu eragiketa hauek:
Egitzazu eragiketa hauek:
- Proposatutako ariketak
7. Bitez polinomio hauek :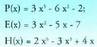 Kalkulatu :
Kalkulatu :
I V. 5. Polinomio baten eta monomio baten arteko biderkaketa.
Polinomio bat monomio batez biderkatzeko, monomioa, polinomioko gai bakoitzez biderkatzen da.Ebatzitako ariketa.9. Egitzazu adierazitako eragiketak :
IV 6. Polinomioen arteko biderkaketak.
n mailako P(x) polinomioak p mailako beste E(x) polinomioarekin
egindako biderkaketaren emaitza edo biderkadura, beste
polinomio bat da eta honen maila, biderkatzaileek dituzten mailen
batura da, hots, n+p.Bedi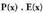 biderkaketa,
biderkaketa,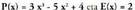 izanda.Eragiketa hori egiteko, polinomioak, zenbaki osoen biderkaketak
egiteko bezalaxe ipiniko dira idatzita, falta zaizkien gaien artean
haiek idazteko moduko lekuak edo hutsuneak utziz. Gero, polinomio
bakoitzeko lehenengo gaia beste polinomioko gai guztiez
biderkatzen da banaka-banaka eta emaitza horiek guztiak batuketarako
bezala idazten dira mailen arabera zutabeetan. Ondoren
azaltzen da ebatzitako ariketa bat :
izanda.Eragiketa hori egiteko, polinomioak, zenbaki osoen biderkaketak
egiteko bezalaxe ipiniko dira idatzita, falta zaizkien gaien artean
haiek idazteko moduko lekuak edo hutsuneak utziz. Gero, polinomio
bakoitzeko lehenengo gaia beste polinomioko gai guztiez
biderkatzen da banaka-banaka eta emaitza horiek guztiak batuketarako
bezala idazten dira mailen arabera zutabeetan. Ondoren
azaltzen da ebatzitako ariketa bat :
- Proposatutako ariketak
8. Polinomio hauek emanda :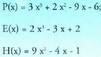 Egitzazu biderkaketa hauek :
Egitzazu biderkaketa hauek :
I V. 7. Polinomioen biderkaketa era laburtuan.
Bi polinomioen arteko biderkaketa egiteko modu lasterragoa
zera da, alegia, koefizienteak bakarrik erabiltzea. Horretarako :• Koadro bat egiten da P(x) eta E(x) polinomioen koefizienteekin.Koadroko laukiak betetzen dira P(x) polinomioko koefiziente
bakoitza E(x) polinomioaren koefizienteez biderkatuz.Geziek adierazten duten moduan, diagonaleko baturak egiten
dira.Bitez polinomio hauek:
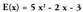 eta
eta Biderkaketaren emaitza, biderkadura, honako hau da :
Biderkaketaren emaitza, biderkadura, honako hau da : Polinomioetakoren bat osoa ez dena denean, lehen adierazi den
moduan jokatzen da, baina beti ere, falta diren gaien koefizienteak
zeroz osatuta.Ebatzitako ariketa.10. Biderkatu
Polinomioetakoren bat osoa ez dena denean, lehen adierazi den
moduan jokatzen da, baina beti ere, falta diren gaien koefizienteak
zeroz osatuta.Ebatzitako ariketa.10. Biderkatu eta
eta era laburtuan.
era laburtuan.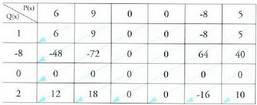 Biderkaketaren emaitza, biderkadura, honako hau da :
Biderkaketaren emaitza, biderkadura, honako hau da :
- Proposatutako ariketak
9. Egin biderkaketa hau :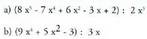 eta
eta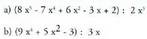
IV.8. Polinomio baten eta monomio baten arteko zatiketa.
Polinomio bat eta haren maila berdineko edo txikiagoko monomioa
emanik, polinomioa monomioaz zatitzeko, polinomioko gai
bakoitza monomioaz zatitzen da eta ateratzen diren zatidura partzialak
batu egiten dira harik eta hondarra zero edota monomioa
baino maila txikiagoko hondar izatera iritsi arte.Ebatzitako ariketa.11. Zatitu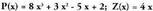 monomioaz.
monomioaz. 4 Zatidura, honako hau da
4 Zatidura, honako hau da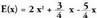 Hondarra berriz,
Hondarra berriz,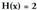 da.Zatiketa orotan bezala, ondoko hau bete behar da :
da.Zatiketa orotan bezala, ondoko hau bete behar da :
- Proposatutako ariketak
10. Egitzazu zatiketa hauek :
IV 9. Bi polinomioen arteko zatiketa.
Bi polinomioen arteko zatidura, orokorki bederen ez da beste
polinomio bat izaten, aurrerago ikusiko dugun moduan, zatiki
razionala baizikBitez: eta
eta E(x) izeneko zatidura polinomioa aurkitu nahi da hau bete dadin :
E(x) izeneko zatidura polinomioa aurkitu nahi da hau bete dadin :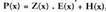 , non :P(x) zatikizuna denZ(x) zatitzaileaE(x) zatidura edo emaitza etaH(x) hondarra. Hondarra, zero edota Z(x) polinomioa baino
maila txikiagoko beste polinomio bat izango da.H(x) zero baldin bada, zatiketa zehatza da eta
, non :P(x) zatikizuna denZ(x) zatitzaileaE(x) zatidura edo emaitza etaH(x) hondarra. Hondarra, zero edota Z(x) polinomioa baino
maila txikiagoko beste polinomio bat izango da.H(x) zero baldin bada, zatiketa zehatza da eta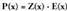 da eta aljebrako batuketa baten bidez biderkaketa lortzen da.Baldin eta,
da eta aljebrako batuketa baten bidez biderkaketa lortzen da.Baldin eta,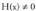 baldin bada, zatidura osoa edota zehazgabea da eta
baldin bada, zatidura osoa edota zehazgabea da eta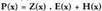 da edota gauza bera dena :
da edota gauza bera dena : Ekuazio horretako bigarren aldea, bi polinomioen arteko zatiketaren
zatidura osoa da.Zatiketa egiteko, P(x) eta Z(x) zenbaki osoak ipintzen diren
bezalaxe jartzen dira. Ondoren, ondoren urratsak jarraitzen dira :1. Zatikizuna eta zatitzailea, x-en berredura beherakorren arabera
ordenatu behar dira.2. Zatikizuna jartzean, lekuak edo hutsuneak utzi behar dira
falta diren gaientzat.3. Zatikizuneko mailarik handieneko gaia, zatitzaileko mailarik
handieneko gaiaz zatitzen da.
Ekuazio horretako bigarren aldea, bi polinomioen arteko zatiketaren
zatidura osoa da.Zatiketa egiteko, P(x) eta Z(x) zenbaki osoak ipintzen diren
bezalaxe jartzen dira. Ondoren, ondoren urratsak jarraitzen dira :1. Zatikizuna eta zatitzailea, x-en berredura beherakorren arabera
ordenatu behar dira.2. Zatikizuna jartzean, lekuak edo hutsuneak utzi behar dira
falta diren gaientzat.3. Zatikizuneko mailarik handieneko gaia, zatitzaileko mailarik
handieneko gaiaz zatitzen da.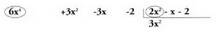 Kasu honetan,
Kasu honetan,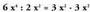 denez,
denez,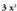 da zatidurako lehenengo gaia.
da zatidurako lehenengo gaia.
4.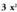 gaia,
gaia,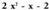 gaiez biderkatzen da eta biderkaketa horren emaitza, zeinuz aldatuta, zatikizunaren azpian kokatu eta hari batzen zaio.
gaiez biderkatzen da eta biderkaketa horren emaitza, zeinuz aldatuta, zatikizunaren azpian kokatu eta hari batzen zaio. 5. Lehenengo hondarra honako hau da :
5. Lehenengo hondarra honako hau da :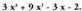 6. 3. eta 4. atalak errepikatu egiten dira, harik eta zero edo
zatitzailea baino maila txikiagokoa den polinomioa hondartzat
lortu arte.
6. 3. eta 4. atalak errepikatu egiten dira, harik eta zero edo
zatitzailea baino maila txikiagokoa den polinomioa hondartzat
lortu arte.
0 Proposatutako ariketak
11. Kalkulatu zatiketa hauetako zatidurak eta hondarrak :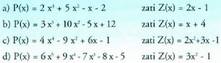
V. Laburbidezko formulak.
Aljebrako bi adierazpenen berdintzari identitate deitzen zaio. Identitate bat, bere letrei edozein balio emanda ere, egiaztatu egiten da. Gainera, letra horiek zeinezkorik gabe, aljebrako zenbakiak edo adierazpenak adieraz ditzakete. Laburbidezko formulak, maiz aurkitzen diren berdintzak dira eta buruz jakitea komeni da.
V. 1. Binomioaren baturaren karratua.
Bitez a eta b edozein zenbaki erreal edota aljebrako adierazpen.
Definizioz :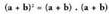 Bi binomioen biderkaketa egiten baldin bada, hau lortzen da :
Bi binomioen biderkaketa egiten baldin bada, hau lortzen da :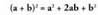 Binomioaren baturaren karratuak, lehen gaiaren karratuagehi lehenengo gaia bider bigarrenaren bikoitza, gehibigarren gaiaren karratua balio du.Ebatzitako ariketak.12. Emaitzazu binomio hauen karratuak.
Binomioaren baturaren karratuak, lehen gaiaren karratuagehi lehenengo gaia bider bigarrenaren bikoitza, gehibigarren gaiaren karratua balio du.Ebatzitako ariketak.12. Emaitzazu binomio hauen karratuak.
- Proposatutako ariketak
13. Emaitzazu binomio hauen karratuak :
V.2. Binomioaren diferentziaren karratua.
Bitez a eta b edozein zenbaki erreal edota aljebrako adierazpen.
Definizioz :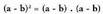 Bi binomioen biderkaketa eginez gero, hau ateratzen da :
Bi binomioen biderkaketa eginez gero, hau ateratzen da :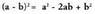 Binomioaren kenduraren edo diferentziaren karratuak,
lehen gaiaren karratua ken lehenengo gaia bider bigarrenaren
bikoitza, gehi bigarren gaiaren karratua balio du.Emaitza horretara halaber, binomioaren baturaren karratuaren
formula erabiliz ere irits daiteke formulan b, (-b)-z ordezkatuta.Horrela, hau aterako litzateke :
Binomioaren kenduraren edo diferentziaren karratuak,
lehen gaiaren karratua ken lehenengo gaia bider bigarrenaren
bikoitza, gehi bigarren gaiaren karratua balio du.Emaitza horretara halaber, binomioaren baturaren karratuaren
formula erabiliz ere irits daiteke formulan b, (-b)-z ordezkatuta.Horrela, hau aterako litzateke :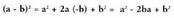 Ebatzitako ariketak.13. Emaitzazu binomio hauen karratuak:
Ebatzitako ariketak.13. Emaitzazu binomio hauen karratuak:
- Proposatutako ariketak
14. Emaitzazu binomio hauen karratuak :
V 3 Bi zenbakien batura bider beren diferentzia.
Karratuen diferentzia.
Bitez a eta b edozein bi zenbaki erreal edota aljebrako adierazpen
. Bi adierazpenen biderkaketa (a+b) • (a-b) egitean, hau lortzen
da : Bi zenbakien batuketak beren diferentziaz biderkatuta
ematen duen biderkadura, lehenengoaren karratua ken
bigarrenaren karratua da.Ebatzitako ariketak.
Bi zenbakien batuketak beren diferentziaz biderkatuta
ematen duen biderkadura, lehenengoaren karratua ken
bigarrenaren karratua da.Ebatzitako ariketak.
14. Egitzazu biderkaketa hauek.
- Proposatutako ariketak
15. Egitzazu biderkaketa hauek.
V.4. Binomioaren baturaren kubua.
 adierazpenak,
adierazpenak, balio du, hau da,
balio du, hau da, Polinomioa binomioaz biderkatzen bada, hau lortzen da :
Polinomioa binomioaz biderkatzen bada, hau lortzen da :
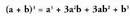 Binomioaren batuketaren kuboak, balio hau du : lehenengo
gaiaren kuboa, gehi lehenengo gaiaren karratuaren
hirukoitza bider bigarren gaia, gehi lehenengo gaiaren
hirukoitza bider bigarren gaiaren karratua, gehi bigarren
gaiaren kuboa.Ebatzitako ariketak.15. Emaitzazu binomio hauen kuboak:
Binomioaren batuketaren kuboak, balio hau du : lehenengo
gaiaren kuboa, gehi lehenengo gaiaren karratuaren
hirukoitza bider bigarren gaia, gehi lehenengo gaiaren
hirukoitza bider bigarren gaiaren karratua, gehi bigarren
gaiaren kuboa.Ebatzitako ariketak.15. Emaitzazu binomio hauen kuboak:
- Proposatutako ariketak
16. Emaitzazu binomio hauen kuboak.
V.5. Binomioaren diferentziaren kuboa.
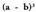 adierazpenak,
adierazpenak, balio du, hau da,
balio du, hau da,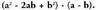 Polinomioa binomioaz biderkatzen bada, hau lortzen da :
Polinomioa binomioaz biderkatzen bada, hau lortzen da :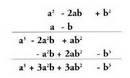
 Binomioaren diferentziaren kuboak, balio hau du : lehenengo
gaiaren kuboa, ken lehenengo gaiaren karratuaren
hirukoitza bider bigarren gaia, gehi lehenengo gaiaren
hirukoitza bider bigarren gaiaren karratua, ken bigarren
gaiaren kuboa.Emaitza horretara, binomioaren batuketaren kuboaren formula
erabiliz ere irits daiteke b, (-b)-z ordezkatuta.Hori eginda honako hau lortuko litzateke :
Binomioaren diferentziaren kuboak, balio hau du : lehenengo
gaiaren kuboa, ken lehenengo gaiaren karratuaren
hirukoitza bider bigarren gaia, gehi lehenengo gaiaren
hirukoitza bider bigarren gaiaren karratua, ken bigarren
gaiaren kuboa.Emaitza horretara, binomioaren batuketaren kuboaren formula
erabiliz ere irits daiteke b, (-b)-z ordezkatuta.Hori eginda honako hau lortuko litzateke :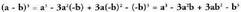 Ebatzitako ariketak.16. Emaitzazu binomio hauen kuboak.
Ebatzitako ariketak.16. Emaitzazu binomio hauen kuboak.
- Proposatutako ariketak
17. Emaitzazu binomio hauen kuboak.
V. 6. Polinomioaren karratua.
Bitez a eta b hiru zenbaki erreal edota aljebrako adierazpen, edoein
. Polinomioaren karratua, definizioz, hau da :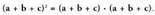 Bi aljebrako adierazpen horien biderkaketa egitean, hau lortzen da :
Bi aljebrako adierazpen horien biderkaketa egitean, hau lortzen da : Polinomioaren karratuak balio hau du : gai bakoitzaren
karratuen batura gehi gai bakoitzaren bikoitza bider beste
gaietako bakoitzarekin lortutako biderkaketen batura.Polinomioaren karratuaren gaietako bat edota bi, zeinu negaboa aurretik dutela egonez gero,
Polinomioaren karratuak balio hau du : gai bakoitzaren
karratuen batura gehi gai bakoitzaren bikoitza bider beste
gaietako bakoitzarekin lortutako biderkaketen batura.Polinomioaren karratuaren gaietako bat edota bi, zeinu negaboa aurretik dutela egonez gero, adierazpenean, ziak beren aurkakoaz edo aurkakoez ordezkatuko ditugu.
adierazpenean, ziak beren aurkakoaz edo aurkakoez ordezkatuko ditugu.
Hau da, honako hau izanez gero :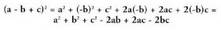 Bestalde,
Bestalde,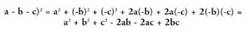 Ebatzitako ariketak.17. Kalkula itzazu karratu hauek.
Ebatzitako ariketak.17. Kalkula itzazu karratu hauek.
- Proposatutako ariketak
18. Kalkulatu karratu hauek.
V.7 Bi kuboen diferentzia.
Bitez a eta b edozein bi zenbaki erreal edota aljebrako adierazpen
. Bi kuboen arteko diferentziak baliokidetza hau du : Egiaztatzeko biderkatu (a - b) binomioa,
Egiaztatzeko biderkatu (a - b) binomioa, trinomioaz.
trinomioaz.
V.8. Bi kuboen batuketa.
Bitez a eta b edozein bi zenbaki erreal edota aljebrako adierazpen
. Bi kuboen arteko batuketak baliokidetza hau du :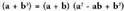 Egiaztatzeko biderkatu (a - b) binomioa,
Egiaztatzeko biderkatu (a - b) binomioa,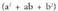 trinomioaz
trinomioaz Kontuz! Ez nahas
Kontuz! Ez nahas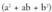 polinomioa
polinomioa binomioaren baturaren karratuarekin, izan ere, azken honek,
binomioaren baturaren karratuarekin, izan ere, azken honek,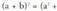
 baitu baliokide. Era berean, ez dira gauza bera
baitu baliokide. Era berean, ez dira gauza bera
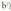 polinomioa eta
polinomioa eta binomioaren diferentziaren karratua, izan ere, azken honek,
binomioaren diferentziaren karratua, izan ere, azken honek,
VI.1. Newtonen binomioa
V puntuan binomioaren karratuaren eta kuboaren formulak
eman dira eta kuboarena, karratuarenetik ondorioztatu da.Binomio baten laugarren berreketa lortzeko, binomioaren kuboarentzat
ateratako emaitza binomioaz biderka daiteke berriro eta
goragoko mailetakoak lortzeko berriz, ostera berriz biderkatuko
genuke eta horrela amaierarik gabe jarraitu. Sistema horrek ordea,
denbora asko eramango liguke eragiketa horiek guztiak egiten.
Gainera, bada formula bat Isaak Newtonek asmatutzat ematen
dena, modu laster eta soil batez edozein binomioren edozein
mailatako berreketa kalkulatzeko balio dena : binomioaren edo
Newtonen binomioaren m-garren berredura ematen digun formula
da.Baina formula hori erabiltzen hasi aurretik, gauza bat gogorarazi behar da, alegia, m elementuren n mailako konbinazioak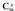 eran izendatzen direla eta baita
eran izendatzen direla eta baita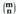 ( m gain n irakurtzen da) ere.
( m gain n irakurtzen da) ere.
Konbinazio zenbaki deitzen zaie eta baita binomio koefiziente ere.. zenbakiari konbinazio zenbakiaren izendatzaile deritzo eta n-ri berriz konbinazio zenbakiaren maila.m! (m faktorial irakurtzen da) idazteak, m zenbakiaren eta 1
zenbakiaren artean kokatutako zenbaki oso guztien arteko
biderkaketa egin behar dela adierazten du.Bedi adibidez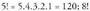 izango bagenu honako hau izango litzateke :
izango bagenu honako hau izango litzateke :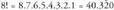 .
.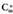 konbinazio zenbakia izanik, honakoa balioa du :
konbinazio zenbakia izanik, honakoa balioa du :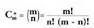 • Adibidez :
• Adibidez : Konbinazio zenbakien gartza bitxi bat zera da,
Konbinazio zenbakien gartza bitxi bat zera da, dela. Hala bada,
dela. Hala bada,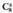 badugu,
badugu,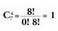 Honaino ezagutzen ditugun binomioen formulak idazten baditugu,
hauek izango ditugu :
Honaino ezagutzen ditugun binomioen formulak idazten baditugu,
hauek izango ditugu : Berdintza hauetan, ondoren adierazten dena ikusten da:
1.Garapena, polinomio ordenatu da, homogenoa eta osoa x eta a-rekiko eta bere maila binomioaren berretzailearena da.2. Garapenaren gai desberdinen koefizienteak edota binomio-koefizienteak,
konbinazio zenbakiak dira. Beren izendatzailea
binomioaren m berretzailearen berdina da eta beren mailak,
zerotik m-rarte handitzen dira.3. Garapenak dituen gai kopurua, m+1 da.m maila duen binomio batentzat formula hori orokortuz gero,
hau izango dugu :
Berdintza hauetan, ondoren adierazten dena ikusten da:
1.Garapena, polinomio ordenatu da, homogenoa eta osoa x eta a-rekiko eta bere maila binomioaren berretzailearena da.2. Garapenaren gai desberdinen koefizienteak edota binomio-koefizienteak,
konbinazio zenbakiak dira. Beren izendatzailea
binomioaren m berretzailearen berdina da eta beren mailak,
zerotik m-rarte handitzen dira.3. Garapenak dituen gai kopurua, m+1 da.m maila duen binomio batentzat formula hori orokortuz gero,
hau izango dugu : .
.
.
.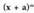 binomioaren garapena baldin badugu berriz, (x + a)"' binomioaren berdina dela esan behar baina zeinuen aldea duela, alegia, zeinuak txandaka aldatuz doazela (gehi eta ken), izan ere, a-ren berredura bakoitiek zeinu negatiboa baitute.
binomioaren garapena baldin badugu berriz, (x + a)"' binomioaren berdina dela esan behar baina zeinuen aldea duela, alegia, zeinuak txandaka aldatuz doazela (gehi eta ken), izan ere, a-ren berredura bakoitiek zeinu negatiboa baitute. Aurreko formula horiek, binomioaren m-garren mailako
berredura ematen digute eta Newtonen binomio izenez ezagutzen
dira. Izan ere, Newton izan haitzen berretzaile ezosoentzat
orokortu zimena, baina dirudienez, Tartaglia-k ondorioztatu edo
asmatu zituen XVI. mendean.Newtonen binomioaren garapenean, n+1-garren lekua duenari
gai orokor deritzo eta batuketa baten berreketaren kasuan, balio
hau du :
Aurreko formula horiek, binomioaren m-garren mailako
berredura ematen digute eta Newtonen binomio izenez ezagutzen
dira. Izan ere, Newton izan haitzen berretzaile ezosoentzat
orokortu zimena, baina dirudienez, Tartaglia-k ondorioztatu edo
asmatu zituen XVI. mendean.Newtonen binomioaren garapenean, n+1-garren lekua duenari
gai orokor deritzo eta batuketa baten berreketaren kasuan, balio
hau du :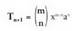 Diferentziaren berreketa baldin bada, gai orokorra, formula honek emana dator:
Diferentziaren berreketa baldin bada, gai orokorra, formula honek emana dator:
V I.2. Binomio koefizienteen arteko erlazioak.
l. Koefiziente bakoitza, bere aurreko koefizientea gai horretan x-ek duen berretzaileaz biderkatu eta kalkulatzen ari den gaian a-k duen berretzaileaz zatituta ateratzen da.
- Adibideak: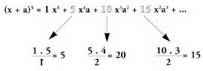 .
.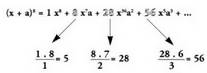 2. Muturretatik hasita distantziakide diren bi gai, berdinak dira.
2. Muturretatik hasita distantziakide diren bi gai, berdinak dira.
Hortik ateratzen da noski, nahikoa dela koefizienteen erdiak
kalkulatzea, izan ere, beste erdiak haien berdinak baina alderantzizko
ordenan izango baitira. baldin badaukagu, 4 gai izango ditugu eta beren koefizienteak : 1 3 3 1 eta nahikoa izango da 1 eta 3 kalkulatzea.
baldin badaukagu, 4 gai izango ditugu eta beren koefizienteak : 1 3 3 1 eta nahikoa izango da 1 eta 3 kalkulatzea. baldin badaukagu, 5 gai izango ditugu eta beren koefizienteak : 1 4 6 4 1 eta nahikoa izango da 1 4 eta 6 kalkulatzea.
baldin badaukagu, 5 gai izango ditugu eta beren koefizienteak : 1 4 6 4 1 eta nahikoa izango da 1 4 eta 6 kalkulatzea. baldin badaukagu, 8 gai izango ditugu eta beren koefizienteak : 1 7 21 35 35 21 7 1 eta nahikoa izango da 1 7 21 eta 35 kalkulatzea.Aurretik adierazi dena, Blaise Pascalek erabilia zuen
baldin badaukagu, 8 gai izango ditugu eta beren koefizienteak : 1 7 21 35 35 21 7 1 eta nahikoa izango da 1 7 21 eta 35 kalkulatzea.Aurretik adierazi dena, Blaise Pascalek erabilia zuen polinomioaren koefizienteak lortzeko, eta era honetara idatz daiteke hark prestatu zuen koefiziente taula :
polinomioaren koefizienteak lortzeko, eta era honetara idatz daiteke hark prestatu zuen koefiziente taula :
VI.3. Taralaren g triangelua
m berretzailea duen binomio baten berreketaren garapenaren
koefizienteen multzoa, era honetan ere idatz daiteke: Itxuragatik triangelu aritmetiko deitzen zaio. Dirudienez,
bere oso antzinakoa da izatez, eta Tartagliak asmatu zuela uste
da.Bistan da noski, koefiziente bakoitza, bere gainean kokatutako
bi koefizienteen batuketa eginez lor daitekeela.Ebatzitako ariketak.18. Garatu binomio hauek :
Itxuragatik triangelu aritmetiko deitzen zaio. Dirudienez,
bere oso antzinakoa da izatez, eta Tartagliak asmatu zuela uste
da.Bistan da noski, koefiziente bakoitza, bere gainean kokatutako
bi koefizienteen batuketa eginez lor daitekeela.Ebatzitako ariketak.18. Garatu binomio hauek :
- Proposatutako ariketak
19. Garatu binomio hauek :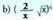 20. Kalkulatu
20. Kalkulatu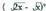 binomio garapeneko 4. gaia.21. Kalkulatu
binomio garapeneko 4. gaia.21. Kalkulatu binomio garapeneko 10. gaia.22. Idatzi
binomio garapeneko 10. gaia.22. Idatzi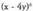
VII. x = ao Balioarentzako polinomioak duen balioa.
P(x) polinomioak balioarentzat polinomioak hartzen duen zenbakizko balioa,
balioarentzat polinomioak hartzen duen zenbakizko balioa,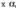 balioaz ordezkatu eta adierazitako eragiketak eginda ateratzen dena da. Zenbaki hori
balioaz ordezkatu eta adierazitako eragiketak eginda ateratzen dena da. Zenbaki hori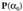 adierazpenaren bidez azaltzen da.• Adibidea:Kalkulatu
adierazpenaren bidez azaltzen da.• Adibidea:Kalkulatu polinomioaren zenbakizko balioa
polinomioaren zenbakizko balioa
VIII. Ordenatutako polinomioa x - a binomioaz zatitzea.
Edozein mailatako polinomioa,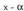 binomioaz zatitu nahi da,
binomioaz zatitu nahi da,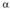 zenbaki ezaguna delarik.Bedi P(x) polinomioa Z(x) binomioaz zatitzeko ariketa,
zenbaki ezaguna delarik.Bedi P(x) polinomioa Z(x) binomioaz zatitzeko ariketa,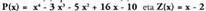 izanik.Zatiketa egiteko, IV.9. puntuan ikusitako urratsak egin behar
dira.1. Zatikizuna eta zatitzailea, x-en berredura beherakorren arabera
ordenatu behar dira.2. Zatikizuna jartzean, hutsuneak utzi behar dira falta diren
gaientzat.3. Zatikizuneko mailarik handieneko gaia, zatitzaileko mailarik
handieneko gaiaz zatitzen da.
izanik.Zatiketa egiteko, IV.9. puntuan ikusitako urratsak egin behar
dira.1. Zatikizuna eta zatitzailea, x-en berredura beherakorren arabera
ordenatu behar dira.2. Zatikizuna jartzean, hutsuneak utzi behar dira falta diren
gaientzat.3. Zatikizuneko mailarik handieneko gaia, zatitzaileko mailarik
handieneko gaiaz zatitzen da.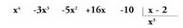 Kasu honetan,
Kasu honetan, . Beraz,
. Beraz,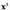 da zatidurako lehenengo gaia.4.
da zatidurako lehenengo gaia.4.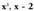 binomioaz biderkatzen da eta emaitza, zeinuz aldatuta, zatikizunaren azpian idatzi eta hari batzen zaio.
binomioaz biderkatzen da eta emaitza, zeinuz aldatuta, zatikizunaren azpian idatzi eta hari batzen zaio.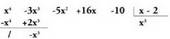 5. Lehenengo hondarra,
5. Lehenengo hondarra,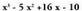 da.6. 3. eta 4. ataletan adierazia errepikatzen da, zero mailako hondarra lortu arte.
da.6. 3. eta 4. ataletan adierazia errepikatzen da, zero mailako hondarra lortu arte.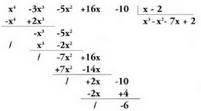 Zatiketa eginda,
Zatiketa eginda,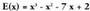 zatidura eta
zatidura eta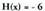 lortu dira.Bedi orain,
lortu dira.Bedi orain,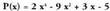 polinomioaren eta
polinomioaren eta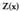
 binomioaren arteko zatiketa.
binomioaren arteko zatiketa. Kasu honetan berriz,
Kasu honetan berriz, zatidura eta
zatidura eta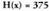
IX. Ruffiniren araua.
Polinomioa, binomioaz zatitzea bizkarrago egiten da askoz ere, RUFFINIren Arazia erabiliz. Arau hori, puntu hauetan laburbil daiteke:1. Zatiduraren lehen gaiaren koefizientea, zatikizunaren
lehen gaiaren koefizientearen berdina da.Aurreko ariketan ikusten denez, zatidurako lehenengo gaiaren
koefizientea, 2 da. Ruffiniren araua aplikatzeko, zatikizunaren koefizienteak
idazten dira eta alboan a ondoren ikus dezakezunez :
binomioaz zatitzea bizkarrago egiten da askoz ere, RUFFINIren Arazia erabiliz. Arau hori, puntu hauetan laburbil daiteke:1. Zatiduraren lehen gaiaren koefizientea, zatikizunaren
lehen gaiaren koefizientearen berdina da.Aurreko ariketan ikusten denez, zatidurako lehenengo gaiaren
koefizientea, 2 da. Ruffiniren araua aplikatzeko, zatikizunaren koefizienteak
idazten dira eta alboan a ondoren ikus dezakezunez : Zatiduraren bigarren gaiaren koefizientea, zatiduraren lehen gaiaren koefizientea bider a gehi zatikizunaren bigarren koefizientea da.
Zatiduraren bigarren gaiaren koefizientea, zatiduraren lehen gaiaren koefizientea bider a gehi zatikizunaren bigarren koefizientea da.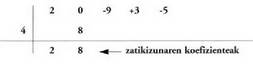 3. Zatiduraren hirugarren gaiaren koefizientea, zatiduraren
bigarren gaiaren koefizientea bider a gehi zatikizunaren hirugarren
koefizientea da.
3. Zatiduraren hirugarren gaiaren koefizientea, zatiduraren
bigarren gaiaren koefizientea bider a gehi zatikizunaren hirugarren
koefizientea da. 4. Orokorki, zatiduraren edozein gairen koefizientea, zatiduraren
aurreko gaiaren koefizientea bider a gehi zatikizunaren
ordena bereko koefizientea da.
4. Orokorki, zatiduraren edozein gairen koefizientea, zatiduraren
aurreko gaiaren koefizientea bider a gehi zatikizunaren
ordena bereko koefizientea da.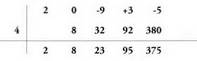 5. Zatiduraren maila, zatikizunarena baino maila bat txikiagoa da.6. Hondarra, zero mailakoa da.Ebatzitako adibideak.19. Egitzazu zatiketak zatiketa normala eginez eta Ruffiniren
arauaz baliatuz.
5. Zatiduraren maila, zatikizunarena baino maila bat txikiagoa da.6. Hondarra, zero mailakoa da.Ebatzitako adibideak.19. Egitzazu zatiketak zatiketa normala eginez eta Ruffiniren
arauaz baliatuz.
- Proposatutako adibideak
20. Egitzazu zatiketak:
X. Polinomio ordenatua x - a binomioaz zatitzearen ondorioak.
Polinomioak koefiziente osoak baldin baditu, binomioaz zatigarri izan dadin, beharrezkoa da gai askea
binomioaz zatigarri izan dadin, beharrezkoa da gai askea -ren multiploa izatea.•
-ren multiploa izatea.•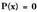 bada, orduan
bada, orduan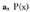 polinomioaren emaitza edo erroetako bat da.• Adibidea: Bedi
polinomioaren emaitza edo erroetako bat da.• Adibidea: Bedi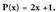
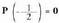 izanda ;
izanda ;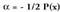 -en emaitza da.Bedi
-en emaitza da.Bedi .
.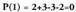 .
.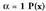 -en emaitza da..
-en emaitza da..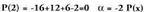 -en emaitza da.1 eta -2, P(x)-en emaitza edo erroak dira.•
-en emaitza da.1 eta -2, P(x)-en emaitza edo erroak dira.•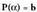 bada, b edozein zenbaki izanda, hondarra b-ren berdina
da. Ondorio hori, HONDARRAREN TEOREMA da
eta honela adieraz daiteke :
bada, b edozein zenbaki izanda, hondarra b-ren berdina
da. Ondorio hori, HONDARRAREN TEOREMA da
eta honela adieraz daiteke :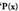 polinomioa
polinomioa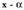 binomioaz
zatitzean gelditzen den zatiketako hondarra,
binomioaz
zatitzean gelditzen den zatiketako hondarra,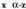 ordezkatuta
ordezkatuta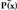
HONDARRAREN TEOREMAREN FROGANTZA.
Lehen ikusi denaren arabera,
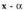 izanik, beraz, honela idatz daiteke :
izanik, beraz, honela idatz daiteke :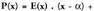
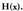 Baldin eta
Baldin eta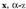 ordezkatzen bada, hau lortzen da :
ordezkatzen bada, hau lortzen da :
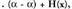 hau da,
hau da,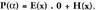 beraz,
beraz,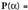
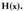 Emaitza hori oso garrantzitsua da, izan ere :•
Emaitza hori oso garrantzitsua da, izan ere :•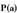 kalkulatzeko Ruffiniren araua erabiltzeko aukera ematen baitu,
kalkulatzeko Ruffiniren araua erabiltzeko aukera ematen baitu,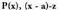 zatitzean emandako hondarra delako.• polinomioa
zatitzean emandako hondarra delako.• polinomioa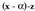 zatitzeko zatigarritasun-baldintza ematen baitu, ezen,
zatitzeko zatigarritasun-baldintza ematen baitu, ezen,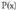 polinomioa
polinomioa zatigarria izateko baldintza,
zatigarria izateko baldintza, ordezkatzean hutsal edo zero baliokoa izatea baita.Ebatzitako adibideak.
ordezkatzean hutsal edo zero baliokoa izatea baita.Ebatzitako adibideak.
20. Kalkulatu zatiketa hauen hondarra, teorema erabiliz. Hondarra = 19, izan ere,
Hondarra = 19, izan ere,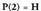 baita.
baita.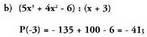 Hondarra = - 41
Hondarra = - 41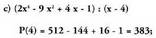 Hondarra = 383
Hondarra = 383
- Proposatutako adibideak.
21. Kalkulatu zatiketa hauen hondarra, hondarraren teorema
erabiliz.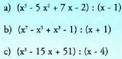 22. Kalkulatu m-ren balioa,
22. Kalkulatu m-ren balioa, zatigarria izan dadin.23. Kalkulatu m-ren balioa,
zatigarria izan dadin.23. Kalkulatu m-ren balioa, zatigarria izan dadin.24. Esan zatiketa egin gabe, zatiketa hauek emaitza
zehatza izango duten ala ez:
zatigarria izan dadin.24. Esan zatiketa egin gabe, zatiketa hauek emaitza
zehatza izango duten ala ez: