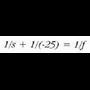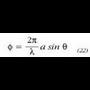Fisika-Kimika»Fisika - Kimika
3. Tresna optikoak
Argazki kamerak, mikroskopioak, teleskopioak eta giza begia dira tresna optiko ezagunenak. Gisa horretako tresnetan lenteak erabiltzen dira eta zenbait kasutan, baita ispiluak ere. Oro har, tresnetako lente eta ispilu horiek handiak izaten dira argiaren uhin luzeraren aldean, eta horregatik, optika geometrikoa erabili ahal izango da tresna horiek aztertzeko. Atal honetan, gehien erabiltzen diren tresna optikoak eta tresna optiko arruntenak aztertuko dira: begia, lupa, mikroskopioa, Galileoren astronomia teleskopioa, teleskopioa eta argazki kamera.
Begia
Begia da, zalantzarik gabe, garrantzi handieneko sistema optikoa. Begiaren osagaiak 1. irudian agertzen dira.
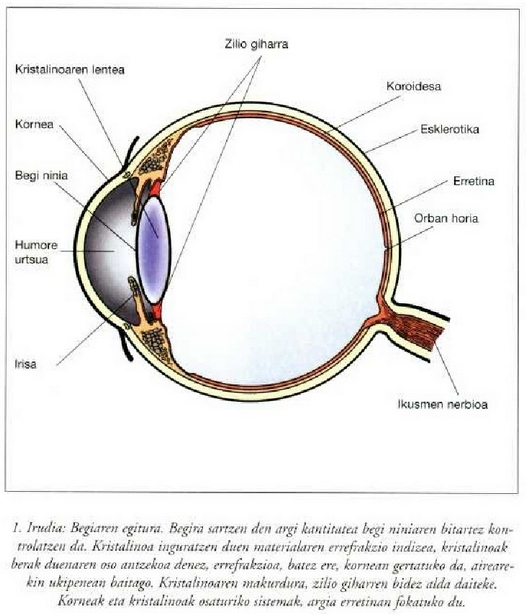
(hannore beirakara eta humore urtsua) uraren errefrakzio indize bera clute ia, 1.34 hain zuzen, eta kristalinoak 1.44-koa. Argia begi nini deritzon irekiduratik sartzen da begira, eta kristalinoak eta korneak osaturiko lente sistemak fokatzen du argia erretinan. Beraz, irudiak erretinan eratzen dira. Erretinak argazki xafla baten gisako zeregina du, eta kono eta makilatxo deritzen egitura sentikorrez osaturik dago; egitura horiek jasotzen dute irudia, eta ondoren, informazioa garunera bidaltzen dute ikusmen nerbioan barrena. Bestalde, kristalinoaren eitea aldatu egiten da gihar ziliarren eraginez ; urrun dagoen objektu bat fokatzeko gihar ziliarra lasaitu egiten da, eta kristalinoak bere distantzia fokalik handiena azaltzen du, 25 mm-koa gutxi gorabehera (korneatik erretinarainoko distantzia, alegia). Fokatu behar den objektua begitik hurbil dagoenean.
berriz, gihar ziliarrak uzkurtu egiten dira, kristalinoaren makurdura erradioa handitu egiten da, eta horren ondorioz kristalinoaren foku distantzia txikitu egiten da. Gihar ziliarren eta kristalinoaren aldaketen helburua, jakina, kasu guztietan erretinan irudia eratzea da. Kristalinoaren tasun berezi horri moldakortasuna deitzen zaio. Hala ere, moldakortasunak badu bere muga ere; objektua begitik gertuegi badago, ezinezkoa da objektuaren irudia erretinan fokatzea, eta lortuko den irudia lausoa izango da. Gizakiak zehatz eta garbi ikus dezakeen punturik hurbilenekoari puntu hurbila deritzo. Kalkuluak egiteko eta, puntu hurbila 25 cm-ra dagoela jo ohi da, oro har. Baina, berez, puntu hori gero eta urrunagokoa izango da pertsona zenbat eta zaharragoa izan, adinarekin kristalinoak moldakortasun ahalmena galtzen baitu. Ondoko taulan puntu hurbilaren eta adinaren arteko erlazioa azaltzen da, balio estatistikoetan:

Gizakiak, bi begi dituenez, badu beste ahalmen bat ere: rkusmen estereoskopikoa. Hau da, nahiz eta begi bietara objektu berberaren informazioa iritsi, begiak elkarretatik bereizita daudenez, informazio hori era desberdinean heltzen zaio begi bakoitzari, eta informazioa garunera heltzean, sakontasun sentsazioa lortzen da horri esker, ikusmen estereoskopikoa lortzen da.
Dena dela, orain artean ikusitako ezaugarri guztiak, akatsik gabeko begiari dagozkion ezaugarriak dira, baina, jakina, ez dago begi perfekturik. Hauek dira begiak izan ditzakeen akatsak: miopia, hipermetropia eta astigmatismoa.
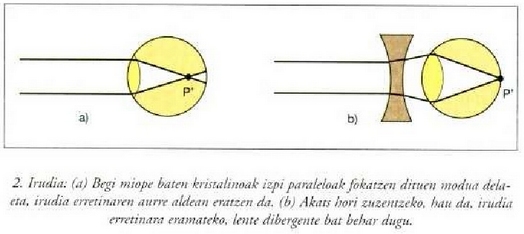
Miopia. Arestian esan den bezala, begi perfektu batek erretinan bertan eratzen du infinituko puntu baten irudia. Batzuetan, ordea, infinituko izpi horiek ez dira erretinan fokatzen, haren aurreko beste punturen batean baizik. Kasu horretan, begia miopea dela esaten da, edo miopia akatsa duela. Miopia zuzentzeko infinitutik datozen izpiak zabaldu egin behar dira begira heldu baino lehen, azken irudia erretinan era dadin. Horretarako, begi aurrean lente dibci gente egoki bat ipini behar da, 2. irudian ikus daitekeen bezala.
Hipermetropia. Kasu honetan infinitutik datozen izpiak erretinan bildu beharrean, haren atzealdean fokatzen dira. Horrelako begi bat, hipei -metropea dela esan ohi da, eta akatsari hipermetropia deritzo. Hipermetropia zuzentzeko, beraz, infinitutik datozen izpiak begira heldu baino lehenago itxi behar dira. Beraz, begi aurrean lente konbergente egoki bat ipini beharko da (ikus 3. irudia).
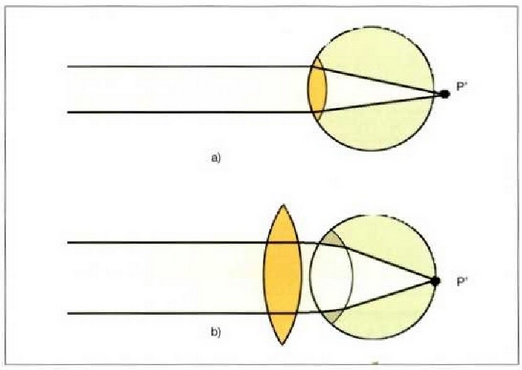
3. Irudia: (a) Begi hipermetrope baten kristalinoak izpi paraleloak fokatzen dituen modua dela-eta, irudia erretinaren atze aldean eratzen da. (b) Akats hori zuzentzeko, lente konbergente bat behar dugu.
Miopia begia luzeegia delako edo kristalinoak kurbatura handiegia duelako ager daiteke, eta hipermetropia, berriz, begia laburregia delako erlo kristalinoak behar besteko ahalmenik ez duelako.
Astigmatismoa. Kornea eta kristalinoa ez elira guztiz esferikoak. Beraz, beren foku distantziak sekzio ezberdinetan zehar ez elira bat etorriko eta ez dute irudi garbirik emango (ikus 4. irudia). Horrelako begi bati astigmatiko deritzo, eta akatsari usti,gmatismo. Akats hori zuzentzeko lente zilindrikoak erabili behar elira, infinitutik datozen izpi guztiak puntu berera hel daitezen.
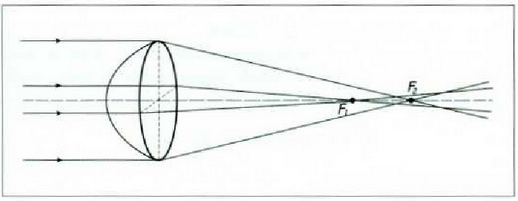
4. Irudia: Astigmatismoa, kornea eta kristalinoa zehazki esferikaak ez direlako sortzen da.
Objektuek izango duten itxurazko neurria irudiak erretinan duen neurriaren araberakoa izango da. Erretinako irudia zenbat era handia;oa izan, aktibatzen diren kono eta makilatxoen kopurua orduan eta handiago izango da, eta ondorioz, objektuaren itxurazko neurria ere bai. 5. irudian ikus daitekeenez,
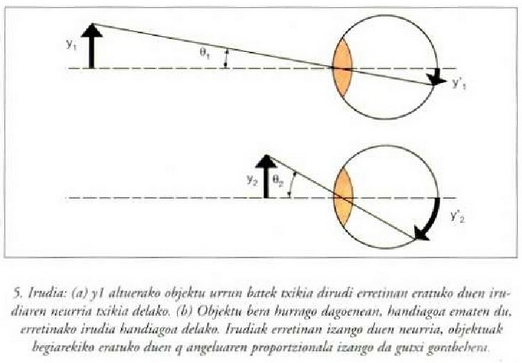
objektuak erretinan izango duen neurria handiagoa izango da objektua begitik gertu dagoenean, eta txikiagoa urrun dagoenean. Objektuaren benetako neurria beti berdina bada ere, itxurazko neurria handitu egiten da objektua begira hurbildu ahala. Baina objektua ezin izango da puntu hurbila baino gehiago hurreratu, irudi garbia lortu nahi baldin bada behintzat; hortaz, objektua puntu hurbilean dagoenean izango da objektuaren bereizmenik onena, eta hortik beherako distantzian ez da irudi garbirik osatuko. Irudiak erretinan duen neurriaren neurketa egoki bat egiteko objektuak begiarekiko eratzen duen angelua neurtu behar da (ikus 5. irudia). Horrela, y garaiera duen objektu txiki bat puntu hurbilean dagoenean, angelu hau eratuko da:
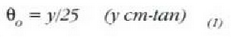
Lehen esan bezala, puntu hurbila 25 cm-ra dagoela hartuko da kontuan eta angelu txikien hurbiltzea
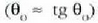 aplikatu ahal izango
da beti
aplikatu ahal izango
da beti
Lupa
Lupa izeneko lente konbergente batekin edozein objekturen itxurazko neurria handi daiteke. 6. irudian, y garaiera cluen objektu txiki bat f foku distantziako lente konbergente mehe baten puntu Fokalean kokatu da.
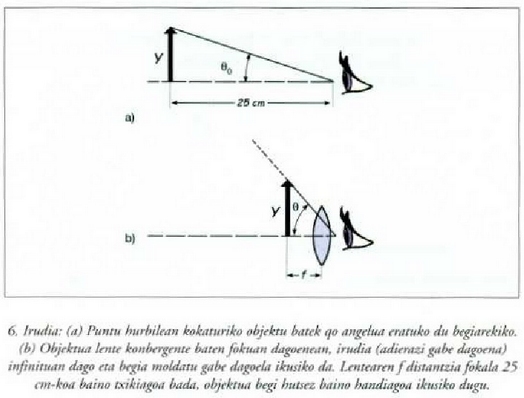
Baldin eta f distantzia puntu hurbilari dagokion distantzia baino txikiagoa bada (25 cm), lente konbergenteak eratuko duen irudia, alegiazkoa, zuzena izango da eta infinituan egongo da, eta irudi hori, kristalinorako objektu modura hartuz, moldapenik gabe, irudia erretinan eratuko da. Irudi horrek hegiarekiko eratuko duen e angelua hau izango da:
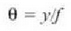
Hortaz, objektuak, lupaz begiratzean, handiagoa ematen du, erretinan eratutako irudia
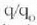 neurrian handitzen baita
(
neurrian handitzen baita
( 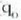 aldagaia ( I) adierazpenean
erabili dena da, eta hegi hutsez izan daitekeen bereizmenik onena ematen du aditzera).
aldagaia ( I) adierazpenean
erabili dena da, eta hegi hutsez izan daitekeen bereizmenik onena ematen du aditzera).
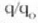 zatidurari zatidurari lentearen
handitze angeluarra edo ahalmena deritzo eta M ikurraz adierazten da:
zatidurari zatidurari lentearen
handitze angeluarra edo ahalmena deritzo eta M ikurraz adierazten da:
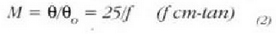
Arestian esan bezala, f < 25 denez, M > 1 izango da.
Erretinan eratzen den irudiaren neurri angeluarra handitu egin daiobjektua F fokuaren eta luparen artean jarriz gero.Kasu honetan, lente konbergenteak sorturiko alegiazko irudia begitik hurbilago egongo da, eta horrela erretinan sortuko den irudiaren neurri angeluarra handitu egingo da, kristalinoaren moldakortasun ahalmenari esker. Lupak sorturiko alegiazko irudia begiaren puntu hurbilean balego, handitze gorena lortuko litzateke (ikus 7. irudia).
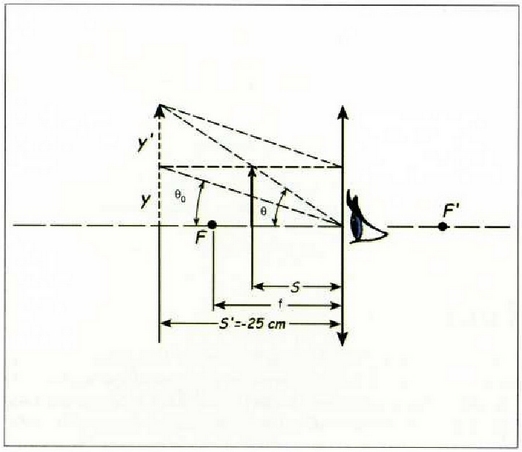
Kasu horri dagokion handitzearen balioa kalkulatzeko, aurreko atalean ikusitako (12) adierazpenetik abiatuta, s' = -25 cm jarri eta ondoko kalkulua egin beharko da:
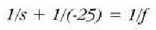
edo
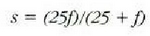
Irudiak begiarekiko eraturiko 6 angelua, 6 = y/s da.
Ordezkaketa eginez, q = (25 + f)y/(25f), eta handitze angeluarra:
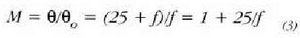
Lupak lente okular gisa erabiltzen dira mikroskopio eta astronomia teleskopioetan, beste lente batek edo lente multzo batek eraturiko irudia ikusteko. Aberraziorik gerta ez dadin, lupak, oro har, ez dira lente bakar batez osaturik egoten, lente bat baino gehiago izaten dituzte. Lente multzoak baldintza bat bete behar du, lenteen foku distantzia erresultantea positiboa izatea, hain zuzen ere. Azkenik, giza begiaren puntu hurbila 25 cm baino urrunago badago, hemen ikusitakoa baino handitze angeluar handiagoa emango du lupak.
Mikroskopioa
Mikroskopioa da objektu oso txikiak begiratzeko erabiltzen den tresna optikorik ezagunena.
Nahiz eta mikroskopioa sistema nahiko konplexua izan ohi den, bi lentez osaturiko sistema
gisa aztertuko da hemen: aurrealdeko lentea objektiboa izango da, eta atzekoa, okularra.
Objektiboaren eta okularraren arteko egokitzapena 8. irudian ikus daitekeen moduan egiten da,
hau da, lente objektiboaren irudi fokua, 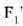 ,
eta okularraren objektu fokua
,
eta okularraren objektu fokua  ,
1 tarteaz banaturik daude. Objektiboaren foku distantzia, okularrarena baino askoz txikiagoa izan ohi da.
,
1 tarteaz banaturik daude. Objektiboaren foku distantzia, okularrarena baino askoz txikiagoa izan ohi da.
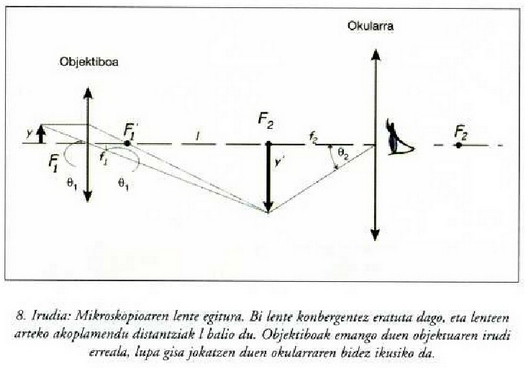
Objektua, objektiboaren objektu distantzia fokaletik kanpo ipintzen da, baina foku horretatik nahi bezain hurbil, dagokion irudia erreala eta neurririk handienekoa izan dadin. Gainera, objektiboak emandako irudi hori, okularraren objektu fokuan eratu behar da, bertatik irten ondoren infinituan eratu dadin eta begiak moldapen beharrik gabe ikus dezan. Begiaren moldakortasun ahalmena kontuan harturik, lupei buruz esandako guztia esan daiteke mikroskopioaren kasuan ere, baina mikroskopioaren handitze edo ahalmenaren kalkulua errazagoa izan dadin, hegiaren moldapenik gabeko egoera hartu da hemen.
Mikroskopioaren handitze angeluar osoa kalkulatzeko ondoko kalkulu hau egin beharko da:
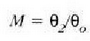
non 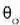 , begi hutsez,
objektua begiaren puntu hurbilean kokatuz, objektuak begiarekiko eratutako angelua den,
eta
, begi hutsez,
objektua begiaren puntu hurbilean kokatuz, objektuak begiarekiko eratutako angelua den,
eta 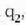 mikroskopioa erabiliz,
dagokion infinituko irudiak begian sortuko lukeen irudiaren anplitude angeluarra. Hortaz,
mikroskopioa erabiliz,
dagokion infinituko irudiak begian sortuko lukeen irudiaren anplitude angeluarra. Hortaz,
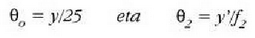
eta handitze angeluarra,
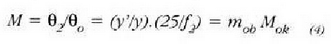
Beraz, mikroskopioaren handitze angeluarra, objektiboak ematen duen albo handitzearen
eta okularrak ematen duen handitze angeluarraren biderkaketaz lortzen da. Bestalde, 8. irudiari begiratuz,
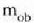 aldagaia beste era honetan ere lor daiteke:
aldagaia beste era honetan ere lor daiteke:
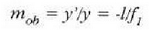
Horregatik, bada, (4) adierazpena honela eman ahal izango da:
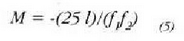
non distantzia guztiak zentimetrotan neurtu behar diren. Handitzea magnitude negatiboa izango da, azken irudia alderantzikatua baita Beraz, objektiboaren eta okularraren foku distantziak eta akoplamendu distantzia baino ez dira ezagutu behar mikroskopioaren handitze angeluarra ezagutzeko.
Galileoren astronomia teleskopioa
Izatez, mikroskopioa eta Galileoren astronomia teleskopioa antzekoak dira. Izan ere, biak objektibo batez eta okular batez osaturikdaude, baina bataren eta hestearen helhuruak desberdinak dira. Mikroskopioa oso objektu txikiak ikusteko erabiltzen da, eta astronomia teleskopioa, aldiz, oso urrun dauden objektu handiak ikusteko erabili ohi da, oro har. Astronomia teleskopioaren kasuan, objektua infinituan dagoenez, objektiboak sortzen duen irudi erreala bere irudi fokuan eratuko da. Gainera, irudi foku hori eta okularraren objektu puntu fokala puntu berean jarriz gero, azkenean, irudia infinituan eratuko litzateke, eta begiak, moldatzeko beharrik gabe ikusiko luke irudi hori. Beraz, mikroskopioaren kasuan aipatutako 1 distantzia baliogabea izango da kasu honetan (ikus 9. irudia).
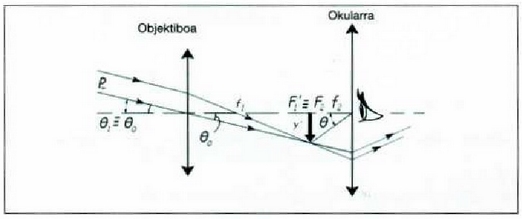
9. Irudia: Galilearen betaurreko astronomikoaren egitura. Kasu honetan ere, bi lente konbergente erabiltzen dira. Egokitzapen distantzia, orain, nulua da.
Betaurrekoaren handitze angeluarra kalkulatu nahi bada, ohiko definizioa hartuko da oinarri, hots,
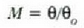
Oraingoan, baina, objektua begiaren puntu hurbilean ipini ezin denez, objektiboarekiko eratzen duen
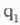 angelua eta begiarekiko eratuko duena (0,),
berdinak direla pentsatuko da. 9. irudiaren arabera,
angelua eta begiarekiko eratuko duena (0,),
berdinak direla pentsatuko da. 9. irudiaren arabera,
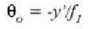
eta
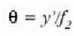
Horren ondorioz,
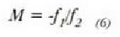
Kasu honetan ere, handitzea negatiboa izango da, irudia alderantzikatua delako.
Bestalde, (6) ekuaziotik atera daitekeenez, astronomia teleskopioa erabilgarria izan dadin,
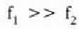 aldintza bete
beharko da.
aldintza bete
beharko da.
Teleskopioa
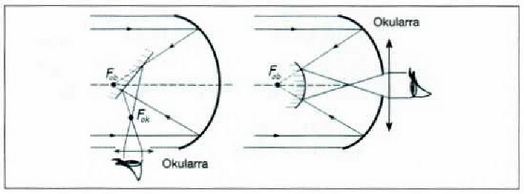
Gaur egun, izarrak eta planetak begiratzeko ispilu esferikoak erabiltzen dira lenteen ordez, lenteak baino askoz errazagoak baitira egiteko. Astronomia teleskopioaren antzekoak dira, baina objektiboaren ordez ispilu esferiko bat dute. Ispiluak eratzen duen irudia, okular batetik ikusten da (10. irudia). Mota desberdinetako tresnakerabil daitezke, baina, kasu guztietan, beste ispilu baten bidez ateratzen dira argi izpiak teleskopioaren hodiaren barnetik, okularrera. Aurreko atalean aipatu denez, batzuetan ispilu parabolikoak erabiltzen dira aberrazioen eragina txikitzeko.
Argazki kamera
Hauek dira argazki kameraren funtsezko osagaiak: kutxa gotor arina, lente konbergente bat, obturadorea eta irudia ezarriko den filma. Kalitate oneko kamerak egiteko lente sistema konplexuak erabili ohi dira, ahal den neurrian aberrazioak zuzentzeko.
Kameren lenteek bi magnitude bereizgarri dituzte. Bata, f foku distantzia da.
Egoera arruntetan, lentearen irudi distantzia eta foku distantzia ia berdinak
direla kontuan hartuz, lentearen albo handitzea (aurreko kapituluko (13) adierazpena)
foku distantziaren proportzionala izango dela ikus daiteke; ondorioz, irudiak filman izango
duen neurria ere f-ren proportzionala izango da. Lentearen bigarren magnitudea, bere d diametroa da.
Normalean, f zenbakiaren arabera zehazten da diametro hori. Esate baterako, f/8 lente batek,
d = f/8-ko diametroa du, hots, diametroa foku distantziaren zortzirena da.
Lenteak argia jasotzeko duen ahalmena, bere gainaldearen proportzionala da, hau da,
diametroaren karratuaren proportzionala. Kamera guztiek, sinpleenak izan ezik, diafragma bat dute,
eta diafragma doituz, lentearen irekidura edo diametro eraginkorra alda daiteke.
Adibidez, f/8 baliotik f/16 baliora pasatzean, diametroa erdira jaitsi da, eta ondorioz, azalera
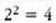 neurrian txikitu. Esposizio denborak lau aldiz handiagoa izan beharko du,
horren arabera, jaso nahi den argi energia osoa alda ez dadin.
neurrian txikitu. Esposizio denborak lau aldiz handiagoa izan beharko du,
horren arabera, jaso nahi den argi energia osoa alda ez dadin.
Lenteen aberrazioak direla eta, aukeratutako objektuaren edozein punturen irudia ez da sekula puntu bakarrekoa izango, lentearen posizioa edo fokatzea edozein direlarik ere. Irudi horrek azalduko cluen neurria txikiagotu egingo da, hots, irudia aratzagoa izango da, lentearen irekidura diafragmaren bitartez txikitzen bada. Baina irekidura txikiak aukeratuz gero, esposizio luzeagoak behar izango dira behar besteko argi energia jaso ahal izateko. Ikus daitekeenez, elkarren aurkako eragina duten faktoreek parte hartzen dutenez, argazkilariak oreka bilatu beharko du, eszena bateko higidura geldiarazteko behar diren esposizio laburren eta aberrazioen eragina murrizteko beharrezkoak diren irekidura txikien artean
4. Optika fisikoa: Interferentzia eta difrakzioa
Optika fisikoak argiaren interferentzia eta difrakzioa aztertzen ditu. Gertaera horien arabera, uhinak eta zatikiak bereizten dira. Atal honetan, argiaren uhin propietateak aztertuko dira; azterketa horretarako lagungarria izan daiteke uhinen zenbait ezaugarri, interferentziarekin eta difrakzioarekin zerikusia Glutenak, gogora ekartzea.
Bi iturrik maiztasun eta uhin luzera bereko baina fase desberdineko uhin armonikoak
sortzen badituzte, eta uhin horiek elkartzen badira, horretatik sortzen den uhina ere
armonikon izango da; eta uhin horren anplitudea hasierako bi uhinen arteko fase eliferentziaren
funtzioa izango da. Fase diferentzia hori baliogabea bada, edo
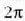 faktorearen anizkoitz osoa bestela,
hi uhinak fasean egongo elira eta bien arteko interferentzia eraikitzailea izango da.
Sortzen den uhin berriaren anplitudea, jatorrizko bi uhinen anplitudeen batura izango da,
eta intentsitatea (anplitudearen koadroaren proportzionala) gehienekoa izango da,
Bestalde, fase diferentzia
faktorearen anizkoitz osoa bestela,
hi uhinak fasean egongo elira eta bien arteko interferentzia eraikitzailea izango da.
Sortzen den uhin berriaren anplitudea, jatorrizko bi uhinen anplitudeen batura izango da,
eta intentsitatea (anplitudearen koadroaren proportzionala) gehienekoa izango da,
Bestalde, fase diferentzia 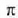 edo
edo 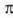 -ren anizkoitz bakoitia bada,
interferentzia desegilea izango da. Halakotan, sortzen den anplitudea uhinen anplitudeen kenduraren
berlina izango da, eta intentsitatea gutxipeko mailakoa. Interferentzia izan duten bi uhinen anplitudea
berdina barla, gehieneko intentsitatea uhin bakoitzaren intentsitatearen laukoitza izango da,
eta gutxieneko intentsitatea, berriz, baliogabea. Bi uhinen artean fase diferentzia izaten da
uhinen ibilbideek luzera desberdinak dituztelako.
Hala,
-ren anizkoitz bakoitia bada,
interferentzia desegilea izango da. Halakotan, sortzen den anplitudea uhinen anplitudeen kenduraren
berlina izango da, eta intentsitatea gutxipeko mailakoa. Interferentzia izan duten bi uhinen anplitudea
berdina barla, gehieneko intentsitatea uhin bakoitzaren intentsitatearen laukoitza izango da,
eta gutxieneko intentsitatea, berriz, baliogabea. Bi uhinen artean fase diferentzia izaten da
uhinen ibilbideek luzera desberdinak dituztelako.
Hala, 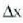 luzera diferentzia dagoenean,
luzera diferentzia dagoenean,
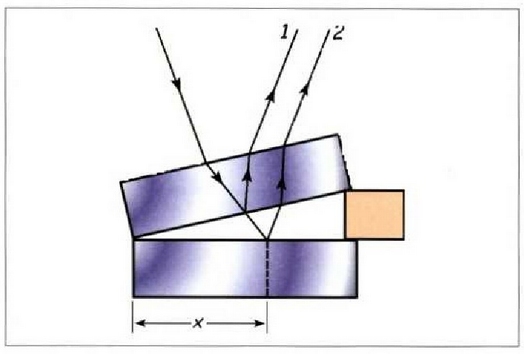
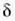 fase diferentzia hau agertuko da:
fase diferentzia hau agertuko da:
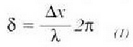
Uhinak muga gainalde batera heltzen direnean islatu egiten elira eta
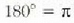 balioko fase aldea gertatzen (la, eta horren ondorioz, fase
diferentzia izaten (la. Hala ere, kontuan hartu behar da hori horrela
dela, baldin eta lehenengo inguruari dagokion uhin lastertasuna
bigarrenari dagokiona baino handiagoa bada.
balioko fase aldea gertatzen (la, eta horren ondorioz, fase
diferentzia izaten (la. Hala ere, kontuan hartu behar da hori horrela
dela, baldin eta lehenengo inguruari dagokion uhin lastertasuna
bigarrenari dagokiona baino handiagoa bada.
Bi iturritatik datozen uhinen arteko interferentzia aztertzeko, iturriek koherenteak izan behar dute, hau da, iturrietatik datozen uhinen arteko f tse diferentziak konstantea izan behar du. Argi izpi bat, oro har, zein bere aldetik irradatzen ari diren miliaka atomoren ondorioa denez, edozein bi atzi iturri ez dira koherenteak izango; iturri harietatik (atazen uhinen arteka fase diferentziak hainbat gorabehera izango ditu segundoko. Koherentzia lortzeko, optikan gehien erabiltzen den metodoa hau da: iturri bakar batetik datorren sarta, hi sarta erlo gehiagotan zatitzen da, eta era horretara sartutako uhinak berrira elkartuz gero, interferentzia diagrama osa daiteke. Sorten zatiketa hori hainbat eratara egin daiteke: kapitulu honetan banan-banan aztertuko dira zatiketa modu hariek. 11a1a, geruza mehe haren hi gainaldeetan gertatzen diren islek eraginclako zatiketa, Michelsonen interferametraaren nondik norakoak, eta oztopa opako batean egindako bi irekidura txikitan gertatzen den difrakzioaren ondorioak aztertuko dira. Azkenik aipatzekoa (la iturri koherenteak lortzeko beste metodo bat, LlolLIen ispilua esaten zaiona hain zuzen.
Interferentzia geruza meheetan
Aire, ur erlo olio genea mehe baten bi gainaldcctan gertatzen olen islaren ondorioz sartzen den argi interferentzia da gehien aztertzenden interferentzia mota. Demagun, ur geruza mehe bat (xaboizko burbuila bat esaterako) norabide zutari buruz angelu txikietan aztertzen ari garela, 1. irudian adierazi den moduan.
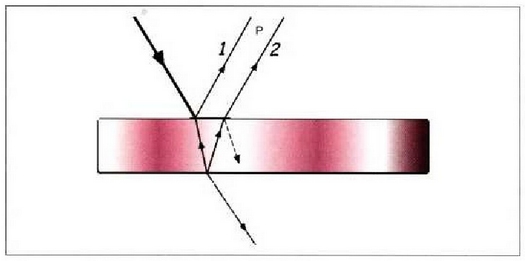
1. Irudin: Geruza mehe baten goiko eta beheko gainaldeetan islaturiko argi izpiak koherenteak izango dira eta interferentziak eragin ditzakete
Argiaren parte bat goiko gainaldean islatzen da. Argia uretan airean baino motelago higitzen Ilenez,
180°-ko fase aldaketa gertatuko da isla horretan. Argiaren beste partea geruzan barrura sartuko da,
eta parte batez beheko ura/airea gainaldean islatuko da. Isla horretan, ordea, ez da fase aldaketarik gertatzen.
Argia gainaldearekiko ia zuta barla, bai goiko gainaldean islatutako izpia, bai behekoan islatua,
P puntuan dagoen begian sar daitezke. Bi izpi horien arteko ibilbide diferentziak gutxi gorabehera
2t-ko balioa du, non t geruzaren lodiera den. Ibilbideen arteko diferentzia horren ondorioz,
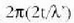 fase diferentzia sortuko da;
fase diferentzia sortuko da;
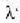 argiak geruzan duen uhin luzera da.
Uhin luzera hori argiak airean duen
argiak geruzan duen uhin luzera da.
Uhin luzera hori argiak airean duen 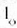 uhin luzerarekin harremana du ondoko adierazpen honen bidez:
uhin luzerarekin harremana du ondoko adierazpen honen bidez:
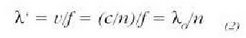
n parametroa, geruzaren errefrakzio indizea da. Bi izpien arteko fase diferentzia,
guztira, 180° gehi ibilbide diferentziak eragindakoa izango da.
Hortaz, 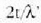 magnitudea baliogabea denean eclo zenbaki osoa denean, interferentzia suntsitzailea gertatuko da;
eta interferentzia eraikitzailea, berriz, ibilbideen diferentzia hori zenbaki erdi osoa denean.
Baldintza horien adierazpen matematikoa hau da:
magnitudea baliogabea denean eclo zenbaki osoa denean, interferentzia suntsitzailea gertatuko da;
eta interferentzia eraikitzailea, berriz, ibilbideen diferentzia hori zenbaki erdi osoa denean.
Baldintza horien adierazpen matematikoa hau da:

Ur geruza mehe bat beirazko gainalde baten gainean dagoenean (ikus 2. irudia), beheka ura/beira gainaldean islatzen den izpiak ere 180º-ko fase aldaketa izango du, izan ere, beiraren errefrakzio indizea (1.5 gutxi gorabehera) urarena (1.33 gutxi gorabehera) baino handiagoa baita.
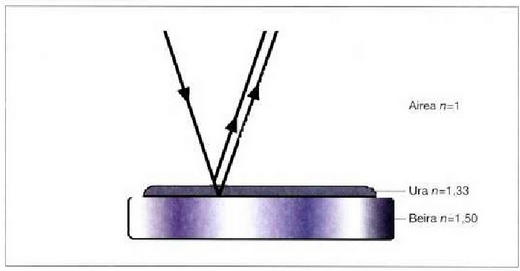
2. Irudia: Beirutiko gainalde batean datzan urgeruzn mehe batean islaturiko iii,(,Tinren roni fcrerztziu. h,rsu honetan, isGttzean izpi biek izango dute 1 R0°-ko fase aldaketa.
Hala, irudian adierazitako bi izpiek, isla gertatu ondoren, 180°-ko fase aldaketa izango dute.
Bi izpi horien arteko fase diferentzia, beraz, ibilbide diferentziaren araberakoa da,
eta era honetan adieraz daiteke: 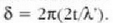
Interferentzia mota horretako adibidea ikus daiteke olio geruza mehe bat ur gainalde baten gainean edo kaleko zoluaren gainean dagoenean. Geruzaren lodiera puntu guztietan berdina ez denez gero, puntu bakoitzaren interferentzia eraikitzailea uhin luzeraren balio desberdinetarako gertatuko da; horregatik ikusten dira askotan koloretako zerrendak.
3. irudian Netclone n eraztrntnk. (zirkulu formako interferentzia lerroak) deituak ikus daitezke. Nola sortzen dira, ordea, horiek?

Horretarako, beirazko bi gainalde behar dira elkarri ukitzen diotela, bata laua eta bestea esferikoa. Bi gainalde horien su-tean geratzen den aire geruza mehean argia islatzen denean ikus daiteke Newtonen eraztunak. Bi gainalclcen ukimen puntuen inguruan beira-airea gainaldean islatutako izpiaren eta beheko airea beira gainaldean islatutakoaren arteko ibilbide diferentzia ia hutsa izango da, edo gutxienv, argiaren uhin luzeraren aldean kontuan ez hartzekoa. Horren o ndorioz. b i uhin horien arteko interferentzia erabat desegilea izango da, beheko airea beira gainaldean islatutako izpiak duen 18(l°-ko fase aldaketa dela-eta. Horregatik eremu hori iluna izango c1:t (diagramaren erdigunea). Lehenengo lerroa • distiratsua, baldintza hau beteko ehien erradiorako azalduko da: dagokion ibilbide diferentziak emango (loen fase diferentziak 180 ° - koa izan behar du. Kontuan hartu behar da fase aldaketa hori lehenago aipatu olen islan gertatzen den beste aldaketari hatu behar zaiola; 360 -ko fase aldaketa (fase aldaketa balio gabearen baliokide) izango da guztira. Beirazko gainalde esferikoaren makurdura erradioa ezagutuz gero. dia;gnunako zerrenden sorleku r,u, tca afera daiteke.
Demagun beirazko bi xafla lau daudela, -i. irudian azaltzen den moduan jarrita. Bi xatlen arteko aire geruzak -ziri itxurakoa- islaren bidez eragiten clituen interferentzia lerroak 5. irudian ikus Gaitezke. Irudian ikusten diren lerroak zuzenak (lira erabilitako beirazko g ainaldeak lauak baitira. Halakoetan, xatl:tk optikoki lauak direla esan ohi da. Hau da. interferentzia zerrenden itxurak xaflen lautasun maila neurtzen du. Adibide gisa. f. irudiko ziriaren antzekoa eratuz kokatutako beirazko bi xafla arruntek eragiten duten diagrama 6. irudian ikus daiteke. Ikus daitekeenez kasu horretan lerro diagrama erabat irregularra da: hortaz, erabilitako xaflak ezin dira optikoki Luiak izan.
4. Irudia: Beirazko bi xaflaren artean dagoen eta falka itxrr»r duen aire geruza mehea. Argiok perpeudrktdarkr erasotzen duela suposatuz, izpien ibilbideen diferentzia irudiko x distantziaren proportzionala izango da. Goruk l (gorrenoz, zerrenda dntnntsrrak eta ihiak iknsrko dim n,rrvlaka.


Michelsonen interferometroa
Interferometroa zehaztasun handiko neurketak egiteko erabiltzen den tresna da; interferentzia lerroak erabiltzen ditu neurketak egiteko. 7. irudian Michelsonen interferometroaren eskema azaltzen da. Puntu jakin bateko iturri batetik datorren argiak A xafla jotzen du.
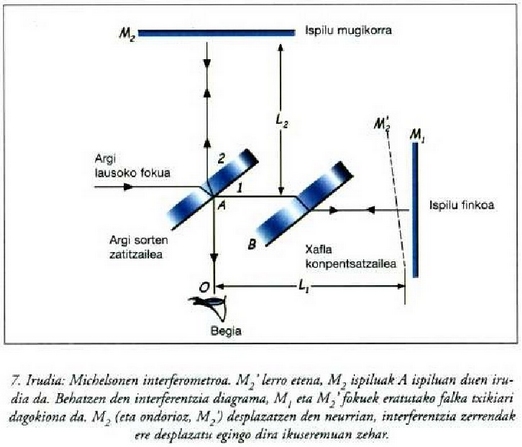
Xafla hori aldez zilarreztatua dagoenez gero, iristen den argi sorta zatitu egin daiteke.
Hala, islatutako izpia 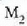 ispilura iritsiko da, eta bertan berriro islatu ondoren, begia dagoen O puntura iritsiko da.
Bestalde, igorritako izpia A-ren lodiera bera duen B xafla konpentsatzailean zehar
ispilura iritsiko da, eta bertan berriro islatu ondoren, begia dagoen O puntura iritsiko da.
Bestalde, igorritako izpia A-ren lodiera bera duen B xafla konpentsatzailean zehar
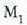 ispilura iritsiko da,
eta ondoren, O puntuko begirantz islatuko da. Aipatutako xafla konpentsatzailea O puntura heldu
behar duten bi izpiek beira lodiera bera zeharka dezaten jartzen da bertan.
ispilura iritsiko da,
eta ondoren, O puntuko begirantz islatuko da. Aipatutako xafla konpentsatzailea O puntura heldu
behar duten bi izpiek beira lodiera bera zeharka dezaten jartzen da bertan.
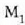 ispilua finko dago,
baina
ispilua finko dago,
baina 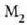 atzera eta
aurrera mugi daiteke doitasun handia duen eta oso ondo kalibratuta dagoen tresna baten bitartez.
Bi izpiak O puntuan elkartzen dira eta interferentzia diagrama bat osatzen dute. Diagrama horren
sorrera azaltzeko kontuan hartu behar da tresnaren argi iturri gisa
atzera eta
aurrera mugi daiteke doitasun handia duen eta oso ondo kalibratuta dagoen tresna baten bitartez.
Bi izpiak O puntuan elkartzen dira eta interferentzia diagrama bat osatzen dute. Diagrama horren
sorrera azaltzeko kontuan hartu behar da tresnaren argi iturri gisa
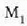 ispilua eta
ispilua eta
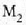 ispiluaren irudia
(eskeman
ispiluaren irudia
(eskeman 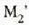 ikurraz adierazitakoa)
har daitezkeela. A ispiluak izpi zatitzaile gisa jokatzen du eta
ikurraz adierazitakoa)
har daitezkeela. A ispiluak izpi zatitzaile gisa jokatzen du eta
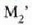 irudi hori ispiluan islatzen den irudia da.
Era horretan, interferometroan gertatzen diren prozesuen interpretazioa asko erraztuko da.
irudi hori ispiluan islatzen den irudia da.
Era horretan, interferometroan gertatzen diren prozesuen interpretazioa asko erraztuko da.
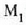 eta
eta
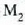 ispiluak elkarzutak badira,
eta izpi zatitzailearekiko distantzia berera badaude,
ispiluak elkarzutak badira,
eta izpi zatitzailearekiko distantzia berera badaude, 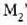 irudia eta
irudia eta 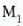 ispilua toki berean egongo dira.
Bestela,
ispilua toki berean egongo dira.
Bestela, 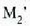 irudiaren lekua aldatuko da pixka
bat eta angelu txiki bat eratuko du
irudiaren lekua aldatuko da pixka
bat eta angelu txiki bat eratuko du 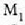 ispiluari buruz,
irudian ikus daitekeen bezala. Hori horrela bada, O puntuan azalduko den interferentzia diagrama 4. irudiko ziri
itxurako aire geruzak sortzen duenaren parekoa izango da (kasu horretan ziria
ispiluari buruz,
irudian ikus daitekeen bezala. Hori horrela bada, O puntuan azalduko den interferentzia diagrama 4. irudiko ziri
itxurako aire geruzak sortzen duenaren parekoa izango da (kasu horretan ziria
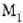 eta
eta
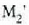 bitartean egongo litzateke).
bitartean egongo litzateke).
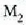 ispilua mugituz gero,
lerro diagrama ere mugitu egingo da. Esate baterako,
ispilua mugituz gero,
lerro diagrama ere mugitu egingo da. Esate baterako, 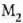 ispilua
ispilua 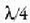 distantzian mugituz gero
(
distantzian mugituz gero
( 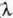 argiaren uhin luzera da),
argiaren uhin luzera da),
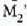 irudia ere
irudia ere
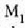 -etik
-etik
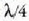 distantziaz urrunduko da, eta ziriaren lodiera
distantziaz urrunduko da, eta ziriaren lodiera
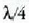 handituko da puntu guztietan.
Hori dela eta, ibilbide diferentziari dagokionez,
handituko da puntu guztietan.
Hori dela eta, ibilbide diferentziari dagokionez, 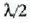 balioko gehikuntza izango du ziriaren puntu guztietan. Zer gertatuko zaio lerro diagramari? Hori ere mugitu egingo da,
lerro erdiari dagokion distantziaz hain zuzen ere; hots, hasieran iluna zen lerro bat distiratsu bihurtuko da.
balioko gehikuntza izango du ziriaren puntu guztietan. Zer gertatuko zaio lerro diagramari? Hori ere mugitu egingo da,
lerro erdiari dagokion distantziaz hain zuzen ere; hots, hasieran iluna zen lerro bat distiratsu bihurtuko da.
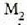 ispilua mugitzen den heinean,
lerro diagrama ere mugitu egiten da. Mugitu den ispiluak egindako distantzia ezagutuz gero, argiaren uhin
luzera lor daiteke. Michelsonek era horretako interferometroa erabili zuen kripton-86 isotopoak igorritako
argiaren uhin luzera neurtzeko metro patroiaren arabera. Ondoren, neurketak zuen doitasunaz jabeturik,
neurketa hori erabili zen metro patroia berriz definitzeko uhin luzeraren arabera.
ispilua mugitzen den heinean,
lerro diagrama ere mugitu egiten da. Mugitu den ispiluak egindako distantzia ezagutuz gero, argiaren uhin
luzera lor daiteke. Michelsonek era horretako interferometroa erabili zuen kripton-86 isotopoak igorritako
argiaren uhin luzera neurtzeko metro patroiaren arabera. Ondoren, neurketak zuen doitasunaz jabeturik,
neurketa hori erabili zen metro patroia berriz definitzeko uhin luzeraren arabera.
Michelsonen interferometroa airearen (edo beste edozein gasen) errefrakzio indizea neurtzeko
ere erabili izan da. Interferometroko izpietako bat hutsa egin daitekeen ontzi batean sartzen da.
Argiak airean cluen uhin luzera hutsean duenarekin 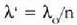 n adierazpenaren bidez eman ohi da; n-k airearen errefrakzio indizea adierazten
du (1 .0003 gutxi gorabehera). Ontzian hutsunea egiten denean,
uhin luzera handitu egiten da, eta ondorioz, distantzia horretan uhin
gutxiago sartuko dira; horrek lerro diagraman leku aldatzea eragingo
du. Leku aldatze hori neurtuz gero, badago errefrakzio indizea
zehaztea. Azkenik, ezin ahaz daiteke Michelsonen interferometroa
erabili zela Lurrak espazioan zuen lastertasun absolutua neurtzeko
Michelson-Morley esperimentu ospetsuan. Esperimentu horrek
Erlatibitatearen teoriarako garrantzi handiko ekarpena egin zuen
n adierazpenaren bidez eman ohi da; n-k airearen errefrakzio indizea adierazten
du (1 .0003 gutxi gorabehera). Ontzian hutsunea egiten denean,
uhin luzera handitu egiten da, eta ondorioz, distantzia horretan uhin
gutxiago sartuko dira; horrek lerro diagraman leku aldatzea eragingo
du. Leku aldatze hori neurtuz gero, badago errefrakzio indizea
zehaztea. Azkenik, ezin ahaz daiteke Michelsonen interferometroa
erabili zela Lurrak espazioan zuen lastertasun absolutua neurtzeko
Michelson-Morley esperimentu ospetsuan. Esperimentu horrek
Erlatibitatearen teoriarako garrantzi handiko ekarpena egin zuen
Bi zirrikituk eragindako interferentzia diagrama
Bi argi iturritatik edo bi baino gehiagotatik datozen argi izpiek interferentzia diagramak sor ditzaten,
iturri guztiek koherenteak izan behar dute, eta horien arteko fase diferentziak konstante iraun behar
du denboran zehar. Arestian esan denez, irrada atomikoa zorizko prozesua da, eta ondorioz,
bi argi iturri desberdin ez dira, oro har, koherenteak izango. Geruza meheetan interferentzia aztertu daiteke
arrazoi batengatik: interferentzia horretan parte hartzen duten bi izpiak islaren bidez zatitu den argi
iturri bakar batetik baitatoz. Argia uhin bidez hedatzen dela frogatzeko Youngek egin zuen bi zirrikituen
esperimentuan, bi iturri koherente lortzeko elkarren paralelo ziren bi zirrikitu argitu zituen argi iturri berberaz.
Zirrikituen zabalera argiaren uhin luzeraren aldean txikia dela onartuko da ondoren. Hala, bi zirrikituetan
gertatuko den difrakzioa dela-eta, zirrikitu bakoitzak iturri lerrozuzenaren portaera izango du
(bi dimentsioko kasuan, iturri puntualaren baliokidea dena). Interferentzia diagrama zirrikituetatik urrun
dagoen pantaila batean ikusiko da. Zirrikituetatik oso urrun dauden puntuetan, bi zirrikituak P puntuarekin
lotzen dituzten lerroak elkarren paralelo direla onar daiteke, eta dagokien ibilbide diferentzia d sin
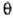 gaiaren berdina izango da gutxi gorabehera,
8. irudian ikus daitekeen bezala. Hortaz, gehieneko interferentziak angelu hauetarako gertatuko dira:
gaiaren berdina izango da gutxi gorabehera,
8. irudian ikus daitekeen bezala. Hortaz, gehieneko interferentziak angelu hauetarako gertatuko dira:
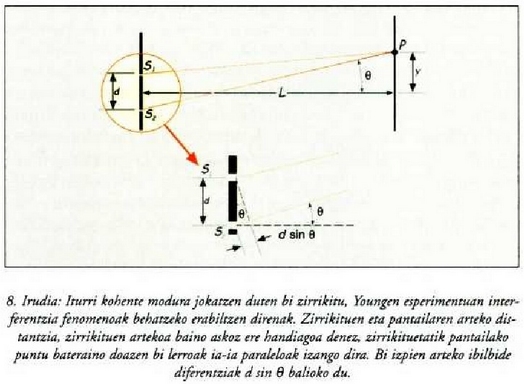
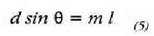
eta gutxienekoak, berriz:
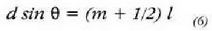
non m = 0, 1, 2, 3,... den. P puntuko fase diferentziari dagokionez, beste adierazpen hau erabil daiteke:
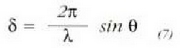
Pantailaren erditik P punturainoko y distantzia (pantailan harrena neurturikoa)
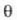 angeluarekin
angeluarekin
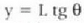 adierazpenaren bidez olago lotuta;
I, parametroa zirrikituetatik pantailara dagoen distantzia ola.
Bestalde,
adierazpenaren bidez olago lotuta;
I, parametroa zirrikituetatik pantailara dagoen distantzia ola.
Bestalde, 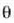 angeluaren balio txikietarako
angeluaren balio txikietarako
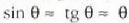 hurbilketa beteko ola.
Beraz,
hurbilketa beteko ola.
Beraz, 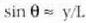 izango ola, eta (7) adierazpena honela geratuko da:
izango ola, eta (7) adierazpena honela geratuko da:
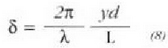
Pantailako edozein P puntutan izango den intentsitatea lortzeko kontuan hartu behar da
fase aldea cluten bi uhin funtzio armonikonen arteko konbinazioa. Uhin elektromagnetikoei
dagozkien uhin funtzioak eremu elektrikoa adierazten cluten bektoreak dira. Demagun pantailako
P puntuan gaudela, 1 zirrikitutik datozen uhinek puntu horretan sortutako eremu elektrikoa
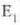 dela, eta 2 zirrikitutik datozenek sortutakoa
dela, eta 2 zirrikitutik datozenek sortutakoa
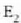 dela.
dela.
Hemen aztertzen diren 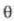 angeluak oso txikiak direnez gero, bi eremuak elkarren paralelo direla onar daiteke,
eta bektore horien moduluak hartu behar elira bakarrik kontuan.
Bi eremu elektriko horiek maiztasun berdinaz oszilatzen clute (zirrikituak argitzen dituen
iturri bakarretik baitatoz biak), eta biek anplitude bera dute, zirrikitu biak neurri berekoak
baitira eta pantailako P puntuarekiko gutxi gorabehera distantzia berera baitaude Uhinen arteko
ibilbide diferentzia argiaren uhin luzeraren ordenakoa izango ola eta eremuen anplitudeei dagokienez, k
ontuan ez hartzeko modukoa. Bestetik,
angeluak oso txikiak direnez gero, bi eremuak elkarren paralelo direla onar daiteke,
eta bektore horien moduluak hartu behar elira bakarrik kontuan.
Bi eremu elektriko horiek maiztasun berdinaz oszilatzen clute (zirrikituak argitzen dituen
iturri bakarretik baitatoz biak), eta biek anplitude bera dute, zirrikitu biak neurri berekoak
baitira eta pantailako P puntuarekiko gutxi gorabehera distantzia berera baitaude Uhinen arteko
ibilbide diferentzia argiaren uhin luzeraren ordenakoa izango ola eta eremuen anplitudeei dagokienez, k
ontuan ez hartzeko modukoa. Bestetik, 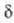 fase diferentzia (7) eta (8) ekuazioek emango dute. Aipatutako uhin funtzioak honela adieraziz gero:
fase diferentzia (7) eta (8) ekuazioek emango dute. Aipatutako uhin funtzioak honela adieraziz gero:
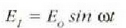 eta
eta 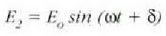
uhin funtzio erresultantea hau izango da:
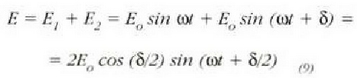
non honako berdintza trigonometriko hau erabili den:
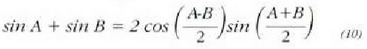
(9) formula aztertuta, ikus daiteke uhin erresultantearen anplitudea
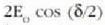 dela.
Horren gehieneko balioa
dela.
Horren gehieneko balioa 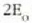 izango da uhinak fasean daudenetan
izango da uhinak fasean daudenetan 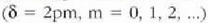 ,
eta baliogabea uhinen arteko fase aldea 180°-koa denean
,
eta baliogabea uhinen arteko fase aldea 180°-koa denean
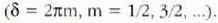 Intentsitatea
anplitudearen koadroarekiko proportzionala denez, P puntuko intentsitatea hau izango da:
Intentsitatea
anplitudearen koadroarekiko proportzionala denez, P puntuko intentsitatea hau izango da:
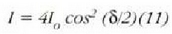
non 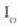 ,
zirrikitu hakar batek, bestearen inolako eraginik gabe, pantailan sortuko lukeen intentsitatea den.
Intentsitateen diagrama nolakoa den ikusi nahi izanez gero, 9. irudia azter daiteke.
Irudi horretan, intentsitatea
,
zirrikitu hakar batek, bestearen inolako eraginik gabe, pantailan sortuko lukeen intentsitatea den.
Intentsitateen diagrama nolakoa den ikusi nahi izanez gero, 9. irudia azter daiteke.
Irudi horretan, intentsitatea 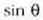 parametroaren funtzioan dago adierazita; gogoan izan behar da
parametroaren funtzioan dago adierazita; gogoan izan behar da
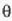 angeluaren balio txikietarako,
angeluaren balio txikietarako,
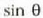 eta y aldagaiak proportzionalak direla.
Gehieneko eta gutxieneko interferentzia askoren batezbestekoa eginez gero,
eta y aldagaiak proportzionalak direla.
Gehieneko eta gutxieneko interferentzia askoren batezbestekoa eginez gero,
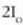 balioa lortuko da
batezbesteko intentsitate gisa, izan ere,
balioa lortuko da
batezbesteko intentsitate gisa, izan ere, 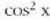 funtzioaren batezbesteko balioa 1/2 baita. Horixe izango litzateke iturri biek sortuko luketen intentsitatea,
baldin eta iturriek, zein bere aldetik, inolako interferentziarik gabe arituko balira.
Hau da, intentsitate hori agertuko litzateke bi iturriak koherenteak ez balira, izan ore,
halakoetan, uhinen arteko fasediferentzian, aipatutako gaiez gainera, beti azalduko hailitzateke
zorizko gorabeherak izango lituzkeen heste gai bat, eta ondorioz,
batezbesteko intentsitatea besterik ez bailitzateke azalduko.
funtzioaren batezbesteko balioa 1/2 baita. Horixe izango litzateke iturri biek sortuko luketen intentsitatea,
baldin eta iturriek, zein bere aldetik, inolako interferentziarik gabe arituko balira.
Hau da, intentsitate hori agertuko litzateke bi iturriak koherenteak ez balira, izan ore,
halakoetan, uhinen arteko fasediferentzian, aipatutako gaiez gainera, beti azalduko hailitzateke
zorizko gorabeherak izango lituzkeen heste gai bat, eta ondorioz,
batezbesteko intentsitatea besterik ez bailitzateke azalduko.
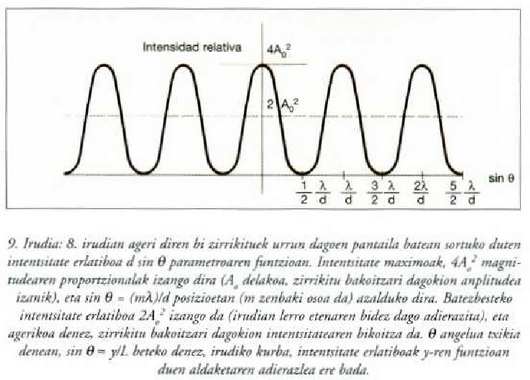
10. irudiko tresnaren bidez -Llo\,den ispilua deitua, hain zuzen-, beste modu batera ere atera daiteke hi zirrikituren interferentzia diagrama.
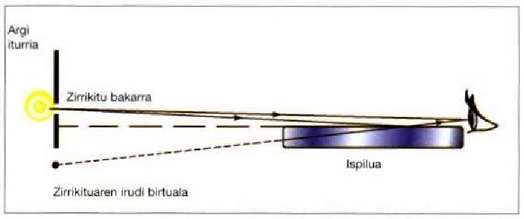
10. Irudia: Argi iturri bikoitz baten interferentziak behatzeko erabiltzen den Lloyden ispilua. Iturri biak (argi iturria era bere irudia) koherenteak dira eta 180 °-ka desfasea dute, islapenari zor zaion fase aldaketa dela eta. Erdiko interferentzi zerrenda, iluna izango da iturrietatik distantziakideak diren puntuetan.
Tresna horretan, zirrikitu bakarra behar da eta ispilu baten planotik gorantz d/2 distantziara
jarri behar da hori. Pantailan (eclo begian) zuzenean jotzen duen iturriak igortzen duen argiaren
eta ispiluan islatutako argiaren artean interferentzia gertatuko da. Islatu den argi hori ispiluak
eratzen duen zirrikituaren alegiazko iruditik datorrela onar daiteke. Ispiluan gertatzen den islak
izango duen 180°-ko fase aldaketa dela eta, sortuko den interferentzia diagrama 180 ° -ko fase
diferentzia cluten bi iturri lerrozuzen eta koherentek eragindakoa izango ola. Alegia, 9. irudian
ageri den diagrama sortuko da, baina diagrama berrian irudi horretako gehieneko eta gutxieneko posizioak
trukaturik agertuko dira. Ispiluaren gain-gainean olagoen posizioari dagokion lerroa iluna izango da,
puntu hori bi iturrietatik distantzia berera egongo baita. Interferentzia eraikitzailea honako puntu
hauetan gertatuko da: ibilbide diferentzia 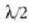 balioaren anizkoivz osoa den
puntuetan alegia. Puntu horietan, ibilbide diferentziari dagokion 180°-
ko fase aldaketa islari dagokion 180°-ko fase aldaketarekin kohinatuko
da eta hortik interferentzia eraikitzailea sortuko da.
balioaren anizkoivz osoa den
puntuetan alegia. Puntu horietan, ibilbide diferentziari dagokion 180°-
ko fase aldaketa islari dagokion 180°-ko fase aldaketarekin kohinatuko
da eta hortik interferentzia eraikitzailea sortuko da.
Uhin armonikoen batuketarako eredu bektoriala
Hiru iturrik, lauk edo lau baino gehiagok sortuko cluten interferentzia diagrama eta zirrikitu bakar batek sortzen duen difrakzioakalkulatzeko, maiztasun bera duten baina fasez aldatuta dauden zenbait uhin armoniko elkartu behar dira. Uhin funtzio armonikoen interpretazio geometriko bat aintzat hartuz gero eta egitura geometriko sinplea erabiliz, maiztasun bereko uhin armonikoen batuketarako metodo orokor bat lor daiteke. Metodo horren bitartez, (10) formula trigonometrikoaren beharrik gabe batu ahal izango dira geometrikoki bi uhin armoniko. Metodo hori hera erabil daiteke uhinen anplitudeak desberdinak direnean edo bi uhin baino gehiago daudenean. Metodoaren oinarria hau da: bi bektoreren erresultantearen y (edo x) osagaia, bektoreen y (edo x) osagaien baturaren berdina da.
Demagun, uhin funtzio hauek ditugula:
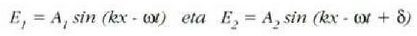
Bi uhin horiek espazioko x puntu batean eta t denbora bitarte jakin batean batzea izango da helburua. Notazioa erraz daiteke kx - wt gaiaren ordez, a idatziz gero. Beraz, batuketa hau egitea izango da helburua:
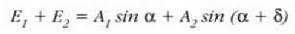
Har dezagun x ardatzarekiko 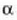 angelua eratzen duen
angelua eratzen duen 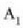 moduluko bektorea (ikus 11. irudia). Bektore horren y osagaia
moduluko bektorea (ikus 11. irudia). Bektore horren y osagaia
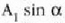 da,
da,
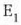 uhin funtzioa hain zuzen.
Era berean,
uhin funtzioa hain zuzen.
Era berean, 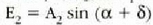 uhin funtzioa x ardatzarekiko
uhin funtzioa x ardatzarekiko
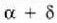 angelua eratuko duen
angelua eratuko duen
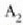 moduluko bektorearen y osagaia izango da.
Batuketa bektorialaren legeak aplikatuz gero, osagai horien batura bektore erresultantearen y
osagaiaren berdina izango da (11. irudia). Bektore erresultantearen y osagaia,
moduluko bektorearen y osagaia izango da.
Batuketa bektorialaren legeak aplikatuz gero, osagai horien batura bektore erresultantearen y
osagaiaren berdina izango da (11. irudia). Bektore erresultantearen y osagaia,
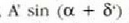 delakoa,
beste uhin funtzio armoniko bat izango da, jatorrizko bi uhin funtzioen baturari dagokiona hain zuzen ere, hots:
delakoa,
beste uhin funtzio armoniko bat izango da, jatorrizko bi uhin funtzioen baturari dagokiona hain zuzen ere, hots:
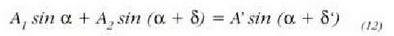
non 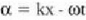 den, eta
den, eta
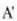 (uhin erresultantearen anplitudea) eta
(uhin erresultantearen anplitudea) eta
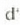 (uhin erresultanteak lehenengo uhinarekiko izango duen fasea)
parametroak jatorrizko uhinak adierazten dituzten bektoreak batuz lor daitezkeen (11. irudian ikus daiteke hori).
(uhin erresultanteak lehenengo uhinarekiko izango duen fasea)
parametroak jatorrizko uhinak adierazten dituzten bektoreak batuz lor daitezkeen (11. irudian ikus daiteke hori).
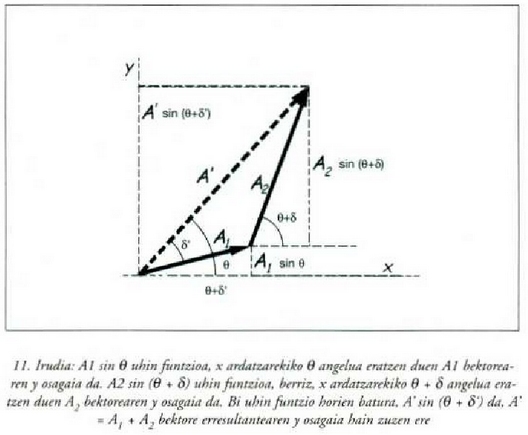
Denborak aurrera egin ahala, 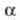 aldatu egingo da. Hortaz, bi uhin funtzioen
adierazle diren bektoreak eta bektore erresultantea biraka
arituko dira plano koordenatuan, haina horien posizio erlatiboak
ez elira aldatuko, bektore guztiek w lastertasun angeluar berberaz
biratuko baitira.
aldatu egingo da. Hortaz, bi uhin funtzioen
adierazle diren bektoreak eta bektore erresultantea biraka
arituko dira plano koordenatuan, haina horien posizio erlatiboak
ez elira aldatuko, bektore guztiek w lastertasun angeluar berberaz
biratuko baitira.
Hiru eta lau iturriren interferentzia diagramak
Demagun, hiru iturri edo gehiago ditugula. Elkarren ondoan dauden iturrien arteko tartea beti bera dela onartuko dugu eta iturri guztiek fasean igortzen dutela. Horrelako sistema batek urrun dagoen pantaila batean sortuko duen intentsitate eskema bi iturrik sortutakoaren antzekoa da, haina garrantzi handiko desberdintasunak dituzte. Gehieneko intentsitateak pantailan izango cluten kokalekua beti berbera izango da, iturrien kopurua edozein dela ere (baina tarte berbera izan behar dute eta fasean igorri behar dute beti). Hala ere, zenbat eta handiagoa izan iturri kopurua, orduan eta handiagoa da gehienekoen intentsitatea, eta orduan eta garbiagoak (estuagoak) dira gehienekoak . Ondoren, hiru eta lau iturrik sortutako eskemak aztertuko dira. Lortutako emaitzak orokortzea ez da gauza zaila iturri kopurua oso handia denean, eta garrantzizko erabilerak ditu difrakzioan eta difrakzio sareetan. Horiek, dena den, aurrerago aztertuko dira.
Lehenbizi, hiru iturriren adibidea hartuko dugu (ikus 12. irudia). Bistakoa denez, adibide horren geometria adierazpena bi iturrien adibideari zegokion bera da.
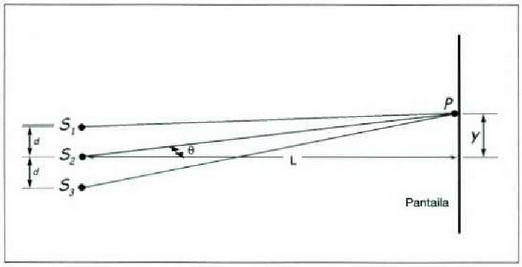
12. Irudia: Distantzia berberaz bananduriko hiru zirrikituk urrun dagoen pantaila batean sortuko duten intentsitate diagrama lortzeka kontutan izan beharreko geometria.
Pantaila iturrietatik urrun jartzen bada, bertako P puntura heltzen diren iturriek igortzen
dituzten izpiak ia elkarren paralelo izango dira. Orduan, lehenengo iturriaren eta bigarrenaren
arteko ibilbide diferentzia 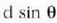 izango da -aurrekoan bezala- eta lehenengo eta hirugarren iturrien artekoa, berriz,
izango da -aurrekoan bezala- eta lehenengo eta hirugarren iturrien artekoa, berriz,
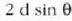 . P puntuko uhin erresultantea,
hiru uhinen batura izango da. Lehenengo uhinak P puntuan izango duen
. P puntuko uhin erresultantea,
hiru uhinen batura izango da. Lehenengo uhinak P puntuan izango duen
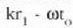 faseari
faseari
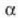 esango diogu;
esango diogu;
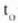 eta
eta
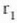 parametroak, behaketarako
denbora bitartea eta lehenengo iturritik P punturainoko distantzia dira, hurrenez hurren.
Hala, gisa horretako hiru uhin batu beharko dira:
parametroak, behaketarako
denbora bitartea eta lehenengo iturritik P punturainoko distantzia dira, hurrenez hurren.
Hala, gisa horretako hiru uhin batu beharko dira:
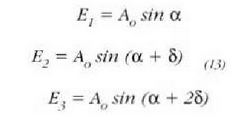
non 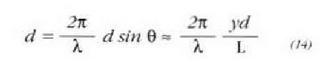 den, bi zirrikituen kasuan bezala.
den, bi zirrikituen kasuan bezala.
Diagrama erresultantea errazago azter daiteke lehen eta bigarren iturrien edo
bigarren eta hirugarren iturrien arteko 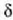 fase angeluaren funtzioan,
fase angeluaren funtzioan, 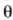 angelu
espazialaren funtzioan baino. P puntu jakin bateko (
angelu
espazialaren funtzioan baino. P puntu jakin bateko ( 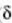 fase angeluaren balio jakin bat izango duena) hiru uhinen anplitude erresultantea ezagutuz gero, aipaturiko fase
angelu hori erraz lotu daiteke
fase angeluaren balio jakin bat izango duena) hiru uhinen anplitude erresultantea ezagutuz gero, aipaturiko fase
angelu hori erraz lotu daiteke 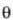 angeluarekin (14) formularen bielez.
angeluarekin (14) formularen bielez.
Hiru uhinen batuketa errazago egingo da batuketarako eredu bektoriala erabiliz gero. Puntu interesgarrienak hauek dira: erahat eraikitzailea den interferentzian sortzen diren puntuak eta erahat desegilea den interferentzian sortzen direnak, hau da, gehieneko eta gutxieneko interferentziak.
Erdiko gehienekoa azalduko den puntuan 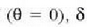 fase angelua baliogabea da eta uhin erresultantearen anplitudea,
berriz, uhin bakoitzaren anplitudearen hirukoitza. Intentsitatea anplitudearen
koadroari buruz proportzionala denez, erdiko gehieneko horri dagokion intentsitatea iturri bakoitzari
dagokiona halako bederatzi izango da. Erdiko gehieneko horretatik urruntzean,
fase angelua baliogabea da eta uhin erresultantearen anplitudea,
berriz, uhin bakoitzaren anplitudearen hirukoitza. Intentsitatea anplitudearen
koadroari buruz proportzionala denez, erdiko gehieneko horri dagokion intentsitatea iturri bakoitzari
dagokiona halako bederatzi izango da. Erdiko gehieneko horretatik urruntzean,
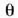 angeluak gora egiten du,
baita
angeluak gora egiten du,
baita 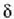 fase angeluak ere.
fase angeluak ere.
13. irudian, 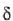 fase angeluak gutxi gorabehera 30°-ko
fase angeluak gutxi gorabehera 30°-ko
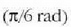 balioa duen kasuari dagokion
batuketa bektoriala aztertzen da.
balioa duen kasuari dagokion
batuketa bektoriala aztertzen da.
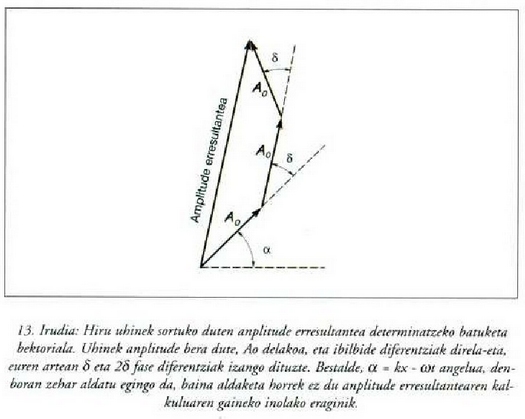
Egoera hori ondoko baldintza betetzen duen 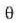 angelua duen P puntuari dagokio:
angelua duen P puntuari dagokio: 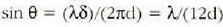 .
Anplitude erresultantea iturri bakoitzaren anplitudearen hirukoitza baino askoz ere txikiagoa da.
.
Anplitude erresultantea iturri bakoitzaren anplitudearen hirukoitza baino askoz ere txikiagoa da.
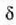 fase angelua handitzen bada,
anplitude erresultantea txikitu egingo da, harik eta
fase angelua handitzen bada,
anplitude erresultantea txikitu egingo da, harik eta 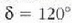 balioan baliogabe bihurtzen den arte. Fase diferentzia hori izaten bada, hiru bektoreek hiruki aldekide bat osatuko dute (14. irudia).
balioan baliogabe bihurtzen den arte. Fase diferentzia hori izaten bada, hiru bektoreek hiruki aldekide bat osatuko dute (14. irudia).
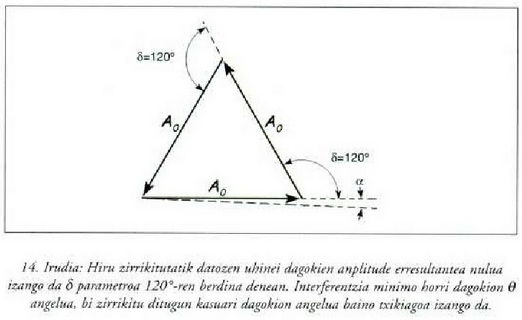
Hortaz, gutxieneko lehenengo interferentzia horri dagokion fase angelua bi zirrikituen
kasuari zegokiona baino txikiagoa da, hartan 180°-koa baitzen.
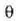 angelua aztertuz gero,
gutxieneko lehenengo interferentzia horrek oraingo kasuan lotuta izango duen
angelua aztertuz gero,
gutxieneko lehenengo interferentzia horrek oraingo kasuan lotuta izango duen
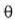 angelua ere aurrekoan zuena baino
txikiagoa izango dela baiezta daiteke. Bestalde,
angelua ere aurrekoan zuena baino
txikiagoa izango dela baiezta daiteke. Bestalde, 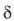 delakoa 120 ° -ko baliotik gora handitzen denean, anplitude erresultantea ere handitu egiten da, eta
delakoa 120 ° -ko baliotik gora handitzen denean, anplitude erresultantea ere handitu egiten da, eta
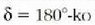 balioan, bigarren mailako gehienekoa izango da.
balioan, bigarren mailako gehienekoa izango da.
Balio horretarako, anplitude erresultantea iturri bakar bati dagokionaren berdina da,
lehen bi iturrietatik datozen uhinek elkar deuseztuko dutenez, hirugarrena bakarrik
geldituko baita. Hortaz, bigarren mailako gehieneko horren intentsitatea erdiko gehienekoak
duenaren bederatziren bat izango da. 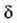 parametroaren balioak 180°-tik gora jarraitzen badu, anplitude erresultantea txikitu egingo da herriz ere,
eta zero bihurtuko da
parametroaren balioak 180°-tik gora jarraitzen badu, anplitude erresultantea txikitu egingo da herriz ere,
eta zero bihurtuko da 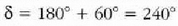 denean.
denean.
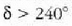 tarteari dagokionez,
anplitudea handitu egingo da, eta iturri bakoitzaren hirukoitza izango da
tarteari dagokionez,
anplitudea handitu egingo da, eta iturri bakoitzaren hirukoitza izango da
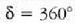 baliorako.
Fase angelu horretan, lehen bi iturrietatik datozen uhinen arteko ibilbide diferentzia uhin
luzera batekoa da, eta lehenengo eta hirugarren iturrietatik datozenen artekoa bi uhin luzeratakoa.
Hiru uhinak, beraz, fasean egongo dira puntu horretan.
baliorako.
Fase angelu horretan, lehen bi iturrietatik datozen uhinen arteko ibilbide diferentzia uhin
luzera batekoa da, eta lehenengo eta hirugarren iturrietatik datozenen artekoa bi uhin luzeratakoa.
Hiru uhinak, beraz, fasean egongo dira puntu horretan.
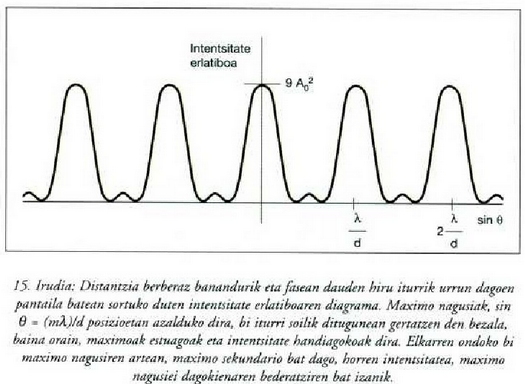
15. irudian iturrietatik urrun
dagoen pantaila batek jasoko lukeen intentsitate diagrama ikus daiteke; horretan gehieneko nagusiak bi
iturrien kasuan azaldutako toki berberetan egongo dira, erlazio honek emango dituen
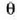 angeluetan hain zuzen:
angeluetan hain zuzen:
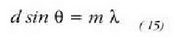
non m = 0, 1, 2,... izango den. (15) adierazpeneko m-ri ordena zenbakia esaten zaio. Geheineko nagusi horiek toki berean badaude ere, hi iturrien kasukoenak baino garaiagoak eta estuagoak izango dira.
Emaitza horiek iturri gehiagotara orokortu daitezke. Esate baterako, lau iturri izanez gero,
gehieneko interferentzia nagusiak, (15) ekuazioaren bidez kalkula daitezke, baina gehieneko horiek,
estuagoak izango dira. Halaber, elkarren ondoko gehieneko nagusi hiren artean, bigarren mailako bi
gehieneko txiki izango lirateke.
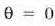 baliorako intentsitate
erresultantea iturri bakar bati dagokiona baino hamasei aldiz handiagoa izango da.
Lehenengo gutxieneko interferentzia
baliorako intentsitate
erresultantea iturri bakar bati dagokiona baino hamasei aldiz handiagoa izango da.
Lehenengo gutxieneko interferentzia 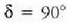 baliorako azalduko da, 16. irudiko diagrama bektorialean ikus daitekeen moduan.
baliorako azalduko da, 16. irudiko diagrama bektorialean ikus daitekeen moduan.
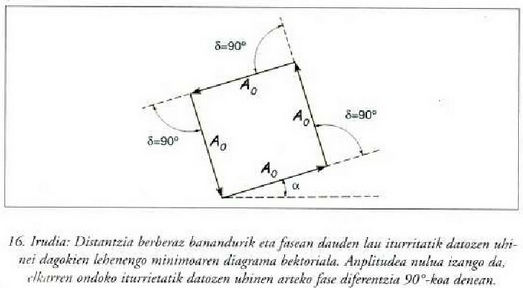
Bigarren mailako lehenengo gehienekoa, berriz, 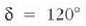
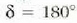 denean, bigarren mailako beste gehieneko bat
denean, bigarren mailako beste gehieneko bat
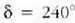 baliotik hurbil eta beste gutxieneko bat
baliotik hurbil eta beste gutxieneko bat
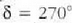 balioan. Ondoren, hurrengo gehieneko nagusia
balioan. Ondoren, hurrengo gehieneko nagusia
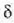 fase angeluak 360°-ko balioa hartzen duenean agertuko da.
Emaitza horiek erakusten clute iturrien kopuruak gora egin ahala, intentsitatea gero eta kontzentratuagoa izango
dela (15) ekuazioak ematen dituen gehieneko nagusietan, eta gainera, gehieneko horiek gero eta estuagoak
izango direla. N iturri hadaude, gehieneko nagusiei dagokien intentsitatea iturri bakar bati dagokiona baino
fase angeluak 360°-ko balioa hartzen duenean agertuko da.
Emaitza horiek erakusten clute iturrien kopuruak gora egin ahala, intentsitatea gero eta kontzentratuagoa izango
dela (15) ekuazioak ematen dituen gehieneko nagusietan, eta gainera, gehieneko horiek gero eta estuagoak
izango direla. N iturri hadaude, gehieneko nagusiei dagokien intentsitatea iturri bakar bati dagokiona baino
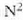 aldiz handiagoa izango da,
eta lehenengo gutxienekoa
aldiz handiagoa izango da,
eta lehenengo gutxienekoa 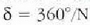 balioan izango da. Kasu honetan hatu beharreko N bektoreek N alde izango dituen poligono itxia osatuko dute.
Bestalde, bigarren mailako gehieneko bat izango da elkarren ondoko hi gutxienekoen artean.
Bigarren mailako gehieneko horiek oso ahulak izango dira gehieneko nagusien aldean.
balioan izango da. Kasu honetan hatu beharreko N bektoreek N alde izango dituen poligono itxia osatuko dute.
Bestalde, bigarren mailako gehieneko bat izango da elkarren ondoko hi gutxienekoen artean.
Bigarren mailako gehieneko horiek oso ahulak izango dira gehieneko nagusien aldean.

(a) Bi (a), hiru (b) eta lau (c) zirrikituk eragindako interferentzia irudiak. (b) kasuan, elkarren ondoko bi maximo nagusiren artean maximo sekundario bakar bat dago, eta (c) diagraman, ostera, gisa horretako bi maximo sekundario.
Zirrikitu bakar batek eragindako difrakzioa
Zirrikituek sortutako interferentzia diagrametan, zirrikitu horien zabalera argiaren uhin
luzera baino askoz txikiagoa zela onartu dugu. Horrenbestez, zirrikituak uhin zilindrikoen
iturri lerrozuzentzat har daitezke, eta erabili ditugun bi dimentsioko diagrametan uhin
zirkularren iturri lerrozuzen gisa agertu dira. Onartutako hipotesi hori bat dator
Huygensen printzipioarekin; azal dezagun zergatik. Demagun zirrikitu hakarra dagoela,
eta argiak ezkerretik eman diola zirrikituari. Printzipio horren arabera, zirrikituaren
irekiduraren eskuin aldean eratzen den uhina lortzeko, irekidura dagoen lerroko puntu bakoitzak
iturri puntualaren joera duela onar daiteke. Hortaz, zirrikituaren ordez, d distantziak banandu
dituen iturri puntualez osatutako lerroa hartuko da. Dakigunez, zirrikituaren zabalera osoa
uhin luzera baino askoz txikiagoa izango da, eta heraz, d distantzia ere uhin luzera baino
askoz txikiagoa izango da. Hortaz, elkarren ondoan diren bi iturri puntuali dagozkien uhinen arteko ibilbide diferentziak ere,
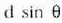 magnitudea alegia,
uhin luzera baino askoz txikiagoa izango dira. Pantailan jasoko diren eta iturri puntual guztietatik
datozen uhinek fase diferentzia kontuan ez hartzeko modukoa izango dute
magnitudea alegia,
uhin luzera baino askoz txikiagoa izango dira. Pantailan jasoko diren eta iturri puntual guztietatik
datozen uhinek fase diferentzia kontuan ez hartzeko modukoa izango dute
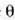 angeluaren balioa edozein
(lela ere; horrela, bada, iturri puntualez osatutako lerro hori iturri puntual bakartzat har daiteke.
angeluaren balioa edozein
(lela ere; horrela, bada, iturri puntualez osatutako lerro hori iturri puntual bakartzat har daiteke.
Haatik, zirrikituaren zabalera eta argiaren uhin luzera ordena berekoak badira, zirrikituaren toki desberdinetatik abiatutako uhinen ibilbide diferentziak aintzat hartu heharko dira. Arestian iturri linealak aztertzean egin diren kalkulu guztiak lagungarriak dira orain ere.
17. irudian a zabalera cluen zirrikitu bakarra adierazi da. Zirrikitua luzera bereko N tarteetan zatitu da.
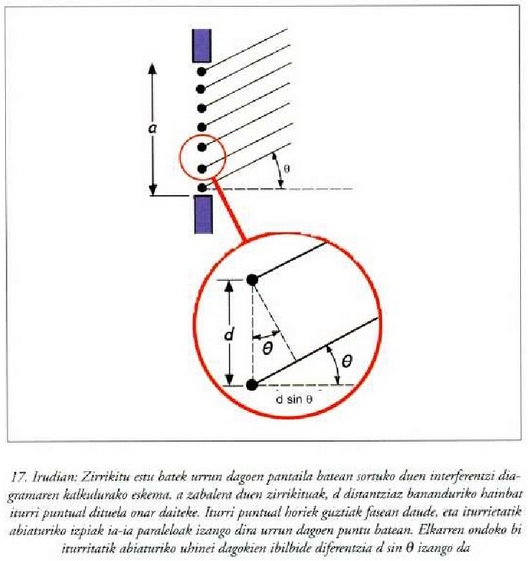
Tarte bakoitzaren erdian uhinak sortuko duen iturri puntual bat dagoela onartuko da (hau da, Huygensen printzipioa aplikatuko da). Elkarren ondokoan diren bi iturri puntualen arteko d distantzia a/N izango da.
N iturri kopurua zenbaki bikoitia dela hartuko dugu oinarri gisa.
Intentsitatea kalkulatzen ari garen lerroa iturrietatik oso urrun dagoenez, iturrietatik abiatzen diren
eta aipatutako lerro horretako P puntura helduko diren izpiak elkarren paralelo izango dira gutxi gorabehera.
Elkarren ondoko edozein hi iturriren arteko ibilbide diferentzia 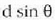 izango da, eta fase diferentzia, berriz,
izango da, eta fase diferentzia, berriz, 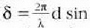
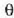 .
Iturri bakar bati dagokion anplitudea
.
Iturri bakar bati dagokion anplitudea 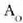 bada, erdiko gehieneko puntuan
bada, erdiko gehieneko puntuan 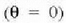 izango den anplitudea
izango den anplitudea 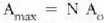 izango da,
puntu horretan uhin guztiak fasean baitaude (ikus 18. irudia).
izango da,
puntu horretan uhin guztiak fasean baitaude (ikus 18. irudia).
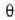 angeluko beste edozein P
puntutako anplitudea lortzeko uhinen batuketaren metodo bektoriala erabilia behar da.
angeluko beste edozein P
puntutako anplitudea lortzeko uhinen batuketaren metodo bektoriala erabilia behar da.
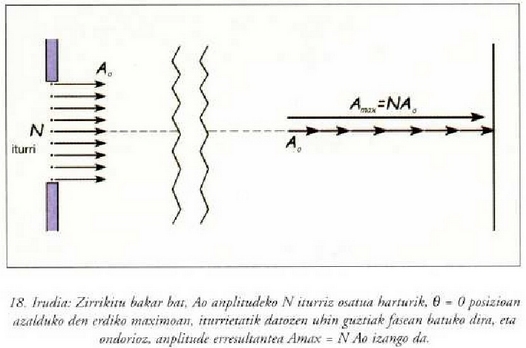
Uhinak adierazten dituzten bektoreek poligono itxi bat osatzen dutenean anplitudea baliogabea izango dela badakigu. Kasu honetan, poligonoak N alde izango ditu (ikus 19. irudia).
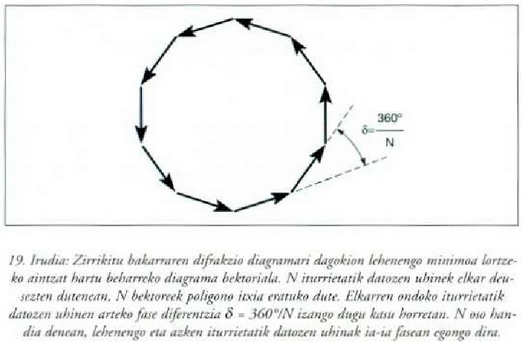
Arrazoibide horretan aurrera egin nahi izanez gero, irudiari begiratuz ondokoaz ohartu beharra dago: P puntuan, irekiduraren goiko aldean dagoen lehenengo iturritik datorren uhinak eta irekiduraren erdiko puntuaren azpian dagoen lehenengo iturritik datorrenak 180°-ko fase aldea izan beharko dute. I lai ditzagun, esaterako, 100 iturri. Iturri horiek baliogabeko intentsitatea (edo anplitudea) emango dute P puntu batean, baldin eta lehenengo iturritik datorren uhinaren eta 51. iturritik datorrenaren arteko fase aldea 180°-koa bada, izan ere, hori hala denean elkar cleuseztuko baitute (ikus 20. irudia).
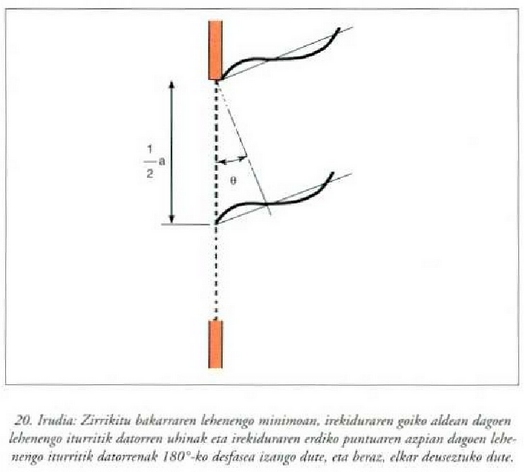
Baldintza hori betetzen bada, bigarren eta 52. iturrietatik datozen uhinek ere 180°-ko fase aldea izango dute,
eta elkar cleuseztuko dute. Gauza bera gertatuko da hirugarren eta 53. iturrien kasuan, etab.
Kasu honetan, gainera, lehenengo iturritik datorren uhinaren eta auken iturritik datorrenaren artean
dagoen fase aldea ia-ia 360°-koa da (fase diferentzia zehatza, 360° - 360°/N (1a). Hala, iturri kopurua
oso handia bada, eta lehenengo eta azken iturrietatik datozen uhinen arteko fase aldea 360°-koa bada,
erabateko deuseztapena gertatuko da. Fase alde hori uhin luzera bateko ibilbide diferentziari dagokio;
ibilbide diferentzia hori 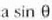 gaiaren berdina denez,
lehenengo gutxienekoa lortzeko baldintza hau bete behar da:
gaiaren berdina denez,
lehenengo gutxienekoa lortzeko baldintza hau bete behar da:
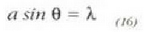
non a zirrikituaren zabalera den. Bigarren gutxienekoa sortuko da goiko eta beheko aldetik datozen uhinen arteko ibilbide diferentzia hi uhin luze direnean. Hori horrela (lela ikusteko, N iturrien multzoa bitan banatu daiteke. Lehenengo zatiko (goiko zatia) iturrietatik datozen uhinen batura baliogabea izango da. Eta era berean, bigarren zatiko (behekoa) iturrietatik datozen uhinen batura ere baliogabea izango da. Hortaz, difrikzio diagramako gutxipekoak honako ekuazio hauen araberakoak izango dira:
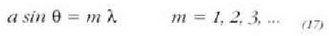
Kalkula dezagun orain, anplitudea puntu orokor batean; puntu horretan, elkarren ondoan eliren bi
iturritatik datozen uhinen arteko fase aldea 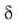 da.
21. irudian kasu horri dagokion bektore diagrama ikus daiteke;
da.
21. irudian kasu horri dagokion bektore diagrama ikus daiteke;
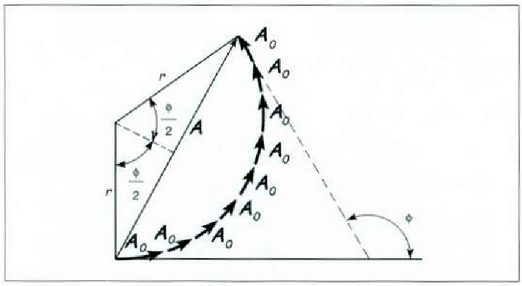
N uhin hatu behar elira, eta uhin horiek lehenengoirekiko izango dituzten fase aldeak
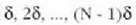 izango elira.
N oso handia eta
izango elira.
N oso handia eta 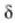 oso txikia direnean,
bektore diagrama zirkunferentzia arku bat da, gutxi gorabehera. Anplitude erresultantea (A) arku horren kordaren
luzera izango da. Anplitude erresultante hori lehenengo uhinaren eta azkenekoaren arteko
oso txikia direnean,
bektore diagrama zirkunferentzia arku bat da, gutxi gorabehera. Anplitude erresultantea (A) arku horren kordaren
luzera izango da. Anplitude erresultante hori lehenengo uhinaren eta azkenekoaren arteko
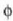 fase diferentziaren funtzioren
arabera kalkulatu ohi da. 21. irudiaren arabera:
fase diferentziaren funtzioren
arabera kalkulatu ohi da. 21. irudiaren arabera:
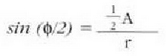
edo

non r arkuaren erradioa den. Arkuaren luzera 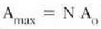 denez eta dagokion angelua f, ondoko hau beteko da:
denez eta dagokion angelua f, ondoko hau beteko da:
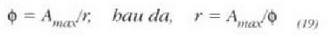
Beraz, azken adierazpena (18) ekuazioaren barruan sartzen bada, hauxe geratuko da:
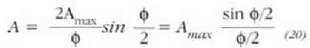
Erdiko puntu gehienekoan 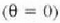 dagoen anplitudea
dagoen anplitudea 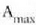 denez, beste
edozein puntutako intentsitatearen eta erdiko gehienekoaren intentsitatearen arteko zatidura honela eman ahal daiteke:
denez, beste
edozein puntutako intentsitatearen eta erdiko gehienekoaren intentsitatearen arteko zatidura honela eman ahal daiteke:
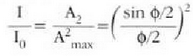
hau da,
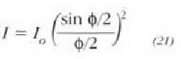
Lehenengo uhinaren eta azkenekoaren arteko  fase diferentziaren eta irekiduraren goiko eta beheko puntuen arteko
fase diferentziaren eta irekiduraren goiko eta beheko puntuen arteko
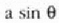 ibilbide diferentziaren arteko harremana hau da:
ibilbide diferentziaren arteko harremana hau da:
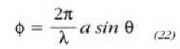
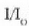 funtzioa 22. irudian azaldu da.
Lehenengo gutxienekoa
funtzioa 22. irudian azaldu da.
Lehenengo gutxienekoa 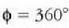 betetzen denean azalduko da,
hau da, irekiduraren goiko eta beheko muturretatik datozen uhinek uhin luzera bateko ibilbide diferentzia guten puntuan
(hor fasean egongo dira).
betetzen denean azalduko da,
hau da, irekiduraren goiko eta beheko muturretatik datozen uhinek uhin luzera bateko ibilbide diferentzia guten puntuan
(hor fasean egongo dira).
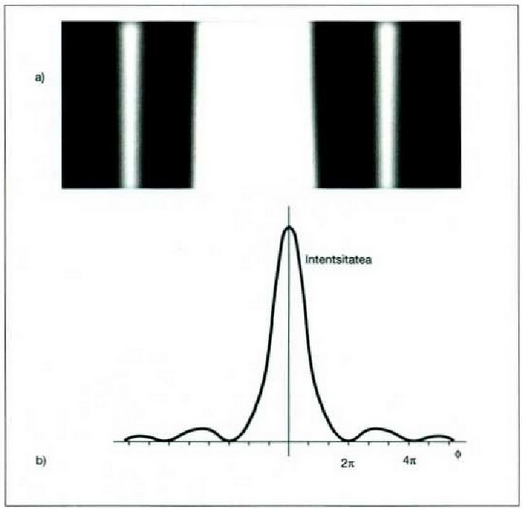
Bigarren gutxienekoa 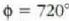 balioari dagokio;
kasu horretan, irekiduraren goiko eta beheko puntuetatik datozen uhinek
balioari dagokio;
kasu horretan, irekiduraren goiko eta beheko puntuetatik datozen uhinek
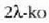 ibilbide diferentzia izango dute.
ibilbide diferentzia izango dute.
Gutxieneko horien arteko erdiko puntuan gutxi gorabehera, higarren mailako gehienekoa izango da. 23. irudian bigarren mailakogehieneko horren intentsitate erlatiboa zehazteko erabil daitekeen bektore diagrama ikus daiteke.
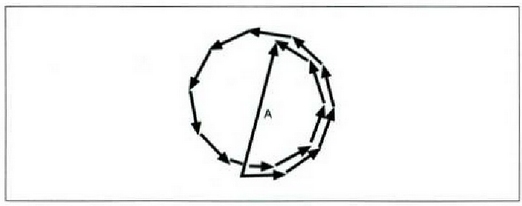
Lehenengo uhinaren eta azkenekoaren arteko fase diferentziak 360 ° + 180° balio du, gutxi gorabehera.
Hau da, bektoreak bira bat eta erdi osatuko du. Anplitude erresultantea irudian ageri clen
zirkunferentziaren A diametroa izango da; zirkunferentziaren C perimetroa
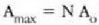 luzera osoaren bi herenak hartuko dituenez, honako hau bete beharko da:
luzera osoaren bi herenak hartuko dituenez, honako hau bete beharko da:
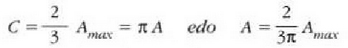
eta
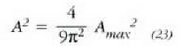
eta puntu horri dagokion intentsitatea hauxe izango da:
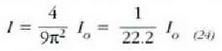
Intentsitate diagramak itxura hau izango du: gehieneko zabala egongo da q = 0 posizioan,
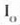 intentsitatearekin;
ondoren, erditik urrundu ahala, intentsitatea txikitu egiten da eta zerora iristen da
intentsitatearekin;
ondoren, erditik urrundu ahala, intentsitatea txikitu egiten da eta zerora iristen da
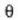 balio honetarako:
balio honetarako:
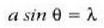
Ondoren, gutxi gorabehera
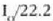 intentsitatea duen bigarren
mailako gehienekoa lortuko da
intentsitatea duen bigarren
mailako gehienekoa lortuko da 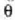 angelu honetarako:
angelu honetarako:
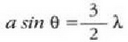
Bigarren gutxienekoa
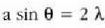 baldintza beteko duen
baldintza beteko duen
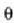 angeluan egongo da.
angeluan egongo da.
22. irudiko intentsitate diagramari zirrikitu bakar baten Fraunhofer difrakzioaren diagrama esaten zaio.
Difrakzio diagrama horren adierazlea den (21) formula lortzeko aintzat hartu diren hipotesiak hauek dira:
(a) uhin lauek elkarzut jotzen dute zirrikitua (izan ere, Huygensen iturri guztien anplitudeak eta faseak
berdinak direla onartu baita) eta (b) diagrama ikusiko den pantailaren eta zirrikituaren arteko
distantzia oso handia da zirrikituaren irekiduraren aldean (iturrietatik abiatuta pantailako eclozein
puntutara heltzen diren izpiak elkarren paralelo direla onartu da, eskemaren geometria errazteko).
Bete beharreko beste baldintza bat hau da: zirrikituaren zabalera eta argiaren uhin luzera ordena berekoak izatea.
Zirrikitua uhin luzera baino askoz zabalagoa bada, lehenengo gutxienekoari cagokion angelua oso txikia izango da.
Adibidez, 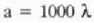 bada,
lehenengo gutxienekoari dagokion
bada,
lehenengo gutxienekoari dagokion 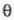 angelua hau izango da:
angelua hau izango da: 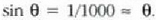 .
Pantaila oso urrun ez badago, antzekoak izango dira hain txikia den angelu hori eta zirrikituaren
goiko eta beheko muturretatik erdiko gehienekora doazen izpiek eratzen dituzten angeluak.
Kontuan izan, onartu dela azken izpi horiek elkarren paralelo direla.
.
Pantaila oso urrun ez badago, antzekoak izango dira hain txikia den angelu hori eta zirrikituaren
goiko eta beheko muturretatik erdiko gehienekora doazen izpiek eratzen dituzten angeluak.
Kontuan izan, onartu dela azken izpi horiek elkarren paralelo direla.
Difrakzio diagrama zirrikitutik hurbil dagoenean, Fresnel difrakzioaren diagrama esaten zaio. Diagrama horren adierazpen geometrikoa dela-eta, Fraunhoferrena baino askoz ere zailagoa da kalkulatzeko. 24. irudian Fraunhofer eta Fresnelen diagramen arteko desberdintasunak azaltzen dira.
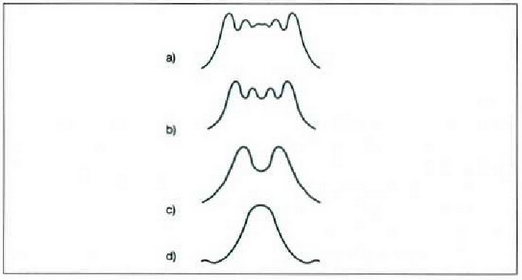
Bi zirrikitu edo gehiago daudenean, urrun dagoen pantaila batean agertuko den intentsitate diagrama zirrikitu bakarrari dagokion difrakzio diagramaren eta dagoeneko azterturik dauden h ainbat zirrikituk eragindako interferentzia diagramaren elkarketa da. 25. irudian, zirrikituetatik urrun dagoen pantaila batean jasotako intentsitate diagrama ikus daiteke (bi zirritu dudenean eta horien arteko d distantzia, zirrikituen a zabaleraren hamarkoitza denean).

25. Irudia: a zabalerako bi zirrikituren interferentzia/difrakzio diagramak, zirrikituen arteko distantzia 10a denean. Erdiko interferentzia maximoaren alde banatara dauden hamargarren interferentzia maxineoak galdu egingo dira, horien posizioa lehenengo difrakzio mininmarenarekin bat datorrelako
Diagrama hori eta 9. irudian dagoen bi zirrikituren (zirrikituak iturri lerrozuzentzat harturik) diagrama berdinak dira, baina diagrama berri hori zirrikitu bakarraren Fraunhofer difrazioaren diagramak modulatuta egongo da. Hortaz, puntu bakoitzeko intentsitatea, bi zirrikituen daiagramako intentsitatearen (11. formulan dagoena) eta zirrikitu bakoitzari dagokion intentsitatearen (21. ekuazioak emandakoa) arteko biderkadura izango da:
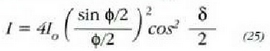
non 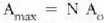 zirrikituen a zabalerarekin
adierazpen honen bidez loturik dagoen:
zirrikituen a zabalerarekin
adierazpen honen bidez loturik dagoen:

eta 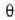 parametroa, zirrikituen arteko
d tartearekin lotuta dagoen, era honetan hain zuzen:
parametroa, zirrikituen arteko
d tartearekin lotuta dagoen, era honetan hain zuzen:
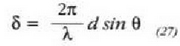
eta 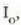 berriz,
berriz,
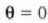 posizioan zirrikituetako
batek (berak soilik) sortuko lukeen intentsitatea den. 25. irudia aztertuz gero, erdiko difrakzio
gehienekoak 19 interferentzia gehieneko dituela ikus daiteke, alegia erdiko interferentzia gehienekoa
eta horren alde banatara beste bederatzi gehieneko. Zergatik kopuru hori? Hamargarren interferentzia
gehienekoari dagokion q angelua honela lortu beharko litzateke:
posizioan zirrikituetako
batek (berak soilik) sortuko lukeen intentsitatea den. 25. irudia aztertuz gero, erdiko difrakzio
gehienekoak 19 interferentzia gehieneko dituela ikus daiteke, alegia erdiko interferentzia gehienekoa
eta horren alde banatara beste bederatzi gehieneko. Zergatik kopuru hori? Hamargarren interferentzia
gehienekoari dagokion q angelua honela lortu beharko litzateke:
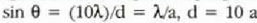 baita. Baina posizio
hori lehenengo difrakzio gutxinekoarekin bat dator eta ezin izango
da ikusi. Horregatik, bederatzi gehieneko ikus daitezke. Hamargarrenak
egon beharko lukeen puntu horretara izpiak bi zirrikituetatik
baletoz, fasean egongo lirateke eta interferentzia eraikitzailea
emango lukete, baina kontua da ez dagoela zirrikituetatik datorren
izpirik, puntu hori difrakzio gutxienekoari baitagokio.
baita. Baina posizio
hori lehenengo difrakzio gutxinekoarekin bat dator eta ezin izango
da ikusi. Horregatik, bederatzi gehieneko ikus daitezke. Hamargarrenak
egon beharko lukeen puntu horretara izpiak bi zirrikituetatik
baletoz, fasean egongo lirateke eta interferentzia eraikitzailea
emango lukete, baina kontua da ez dagoela zirrikituetatik datorren
izpirik, puntu hori difrakzio gutxienekoari baitagokio.
Difrakzioa eta bereizmena
Uhin frontearen zati batek bere ibilbidean edozein motako oztopo edo irekidura bat aurkitzen duenean gertatzen da difrakzioa. Espazioko puntu jakin bateko intentsitatea Huygensen printzipioa erabiliz lor daiteke, uhin fronteko puntu bakoitza iturri puntualtzat hartuz eta sistemari dagokion interferentzia diagrama kalkulatuz. Fraunhoferren diagramak oztopo edo irekiduratik urrun dauden puntuetan ikusiko dira, baldin eta puntu horietara heltzen diren izpiak ia-ia elkarren paralelo badira. Hala ere, bada mota horretako diagramak ikusteko beste modurik, lente bat erabiliz hain zuzen ere. Lente horrek, bere foku puntuan jarritako pantaila batean fokatuko ditu izpi paralelo horiek. Bestalde, iturritik gertu dauden puntuetan Fresnelen diagramak ikusi ahal izango dira. Argiaren difrakzioa ez da argi ikusten den gertakaria, uhin luzera txikia baitu eta argi intentsitatea ez baita izaten behar bezain handia. Horrez gainera, zirrikitu luze eta estu baten Fraunhoferren diagrama izan ezik, gainerako difrakzio diagramak, oro har, kalkulatzen zailak dira.
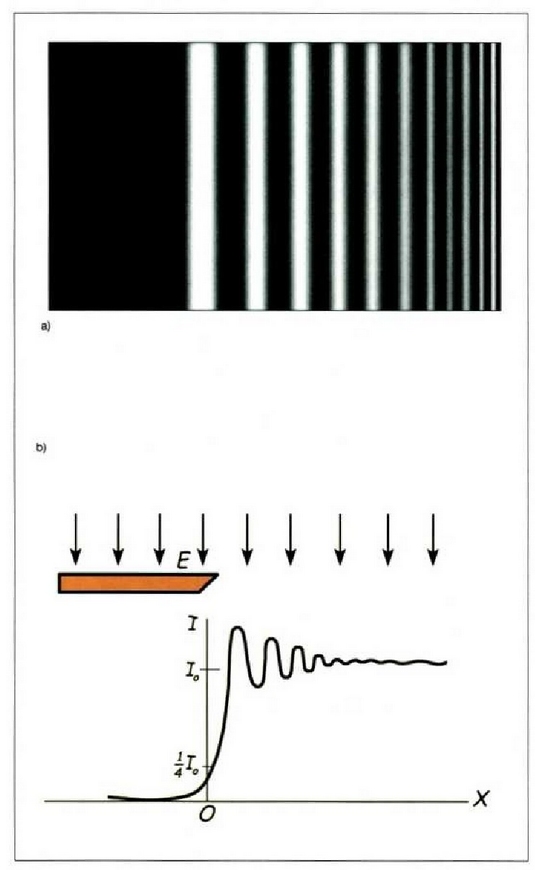
26. Irudia: (a) Ertz lerrozuzen batek eragindako Fresnel difrakzioa. (b) Intentsitatea, ertzaren perpendikularra den lerro batean zehar neurtutako distantziaren funtzioan. 26a irudian ertz lerrozuzen baten Fresnel difrakzioaren diagrama ikus daiteke, iturri puntual batetik datorren argiak eraso egiten dionean. 26b irudian, berriz, ertzaren zuta den lerro bateanneurtutako distantziaren arabera intentsitatea nola aldatzen den azaltzen da. Argi intentsitatea ez da bat-batean zerora jaisten itzal geometrikoan, baina berehala txikitzen da eta ertzetik zenbait uhin luzetara ez da kontuan hartzekoa. 27. irudian Fresnel diagrama aztertzen da irekiclura zirkular batean. Bestalde, irekidura angeluzuzen baten Fresnel difrakzioaren diagrama 28. irudian aztertzen da.

Gisa horretako diagramak ezin elira argi iturri "zabalen" (puntualak ez direnak) bidez aztertu, lanpara gori arrunt baten bidez esate baterako, iturriko puntu batetik catorren argiak eragindako zerrenda ilunak beste puntu batetik datorren argiak eragindako zerrenda distiratsuen gainean jarriko baitira. Hortaz, iturri puntualak beharko dira.

Irekidura zirkular baten Fraunhoferren diagramak (29. irudia) garrantzi handiko aplikazioak ditu tresna optikoen bereizmenerako, izan ere, tresna horietariko askok erabiltzen baitituzte irekiclura zirkularrak.

Lehenengo difrakzio gutxienekoari dagokion 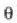 angelua
angelua 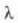 uhin luzerarekin eta irekiduraren
D diametroarekin era honetan lotzen da:
uhin luzerarekin eta irekiduraren
D diametroarekin era honetan lotzen da:
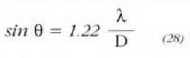
(28) aclierazpena (16) ekuazioaren antzekoa da, 1.22 faktorea izan ezik, kasu honetako aclierazpen geometria
zilindrikoa baita. Bestela, zirrikatu bakarraren kasuan egindako azterketa matematikoa egin behar da.
Aplikazio askotan, 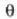 angelua txikia izaten da
eta heste era honetara idatz daiteke azken ekuazioa:
angelua txikia izaten da
eta heste era honetara idatz daiteke azken ekuazioa:
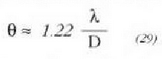
30. irudian, koherenteak ez diren bi iturri puntual eta irekidura zirkular bat adierazi dira; iturriek
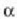 angelua eratzen dute irekidurarekiko,
eta irekiclura eta iturrien arteko distantzia handia da. Irudi berean, Fraunhofer cifrakzioaren intentsitate
diagramak azaldu elira.
angelua eratzen dute irekidurarekiko,
eta irekiclura eta iturrien arteko distantzia handia da. Irudi berean, Fraunhofer cifrakzioaren intentsitate
diagramak azaldu elira. 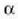 angelua
angelua
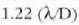 magnitudea baino askoz handiagoa bada,
iturri bien difrakzio irudiek gainezarmen txikia izando dute, eta pantailan, bi argi iturri bereiziko dira garbi-garbi.
magnitudea baino askoz handiagoa bada,
iturri bien difrakzio irudiek gainezarmen txikia izando dute, eta pantailan, bi argi iturri bereiziko dira garbi-garbi.
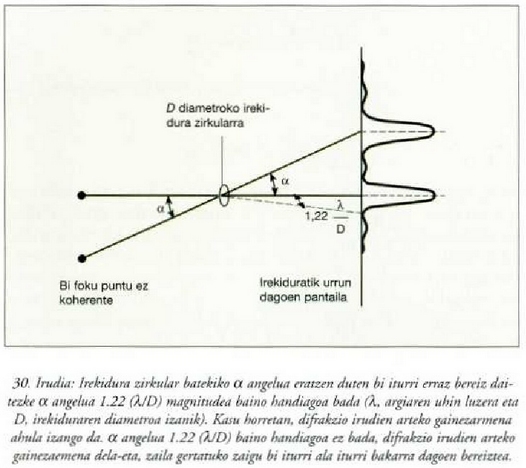
Hala ere, 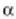 txikitu abala, difrakzio
irudien gainezarmena handitu egingo da; ondorioz, oso zaila izango ola pantailan iturri bat edo bi dauden bereiztea.
Angelu tarte kritiko honetarako:
txikitu abala, difrakzio
irudien gainezarmena handitu egingo da; ondorioz, oso zaila izango ola pantailan iturri bat edo bi dauden bereiztea.
Angelu tarte kritiko honetarako:
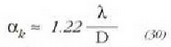
iturri baten difrakzio irudiaren lehenengo gutxienekoa beste iturriaren erdiko
gehienekoaren gainean dago. Halakoetan esaten ola objektuak Ravlcigh izeneko irizpidearen
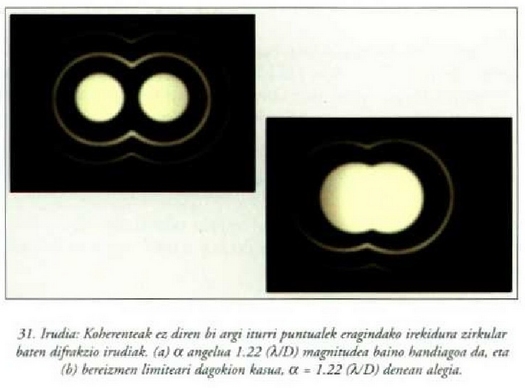
arabera bereizita daudela zehatz-mehatz. 31. irudian, bi iturriren difrakzio
irudiak ikus daitezke, 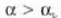 eta
eta 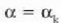 kasuetarako.
kasuetarako.
Tresna optikorik interesgarriena begia
denez gero, eta begininia irekidura zirkulartzat har daitekeenez gero, begiaren bereizmenarekin zerikusia cluen
aciibide bat aztertuko (lit. Begininiaren diametroa 5 mm-koa dela eta erabiltzen ari garen argiaren uhin luzera 600
nnr koa direla oinarri hartuz gero, lor dezagun giza begiari dagokion tarte angeluar kritikoa, hau ola, bi objektu
puntual bereizi ahal izateko behar den gutxieneko tarte angeluarra. Hori lortzeko, (30) adierazpenean azalclutako
balioak zuzenean ordezkatu beharko dira eta 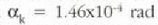 rad balioa lortuko da. Hortaz. bi objektu horiek begitik 100 m-ra badaude adibidez, bien arteko y gutxieneko
distantziak bereizteko honako hau bete beharko litzateke:
rad balioa lortuko da. Hortaz. bi objektu horiek begitik 100 m-ra badaude adibidez, bien arteko y gutxieneko
distantziak bereizteko honako hau bete beharko litzateke:
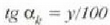
hau da,
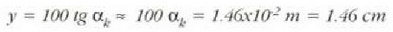
Difrakzio sareak
Difrakzio sareak oso tresna egokiak dira argia aztertzeko. Difrakzio sare bat hainbat
zirrikituk osatzen dute; zirrikitu horien arteko tarte guztiak berdinak dira.
Horrelako sare bat osatzeko modurik errazena hau ola: beira zati batean edo metalezko
xafla batean elkarren paraleloak diren eta elkarren artean tarte bera cluten artekak
moztea cloitasun handiko makina batez. 7,entimetroko 10000 zirrikitu dituzten sareak
aurki daitezke. Horrelako sare batean zirrikituen arteko distantzia
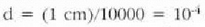 cm da.
Demagun, argi uhin lau batek mota horretako sare batean jotzen duela angelu zuzena osatuz;
zirrikitu bakoitzaren zabalera oso txikia dela hartuko da oinarri, eta oncorioz,
zirrikituak iturri lerrozuzen direla onartuko da; halakoetan lehenago lortutako emaitza
berak aplika daitezke.. Saretik urrun dagoen pantaila batean ikus daitekeen interferentzia
diagrama tarte berberaz banatutako hainbat iturri linealek sortuko dute.
Gehieneko interferentziak
cm da.
Demagun, argi uhin lau batek mota horretako sare batean jotzen duela angelu zuzena osatuz;
zirrikitu bakoitzaren zabalera oso txikia dela hartuko da oinarri, eta oncorioz,
zirrikituak iturri lerrozuzen direla onartuko da; halakoetan lehenago lortutako emaitza
berak aplika daitezke.. Saretik urrun dagoen pantaila batean ikus daitekeen interferentzia
diagrama tarte berberaz banatutako hainbat iturri linealek sortuko dute.
Gehieneko interferentziak 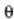 angeluetarako agertuko dira:
angeluetarako agertuko dira:
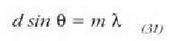
Gehieneko interferentzia baten kokaera ez da iturri kopuruaren mendekoa izango; baina zenbat eta
iturri gehiago izan, orduan eta garbiagoa izango da gehienekoa. Hori horrela dela ikusteko,
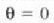 posizioan dagoen erdiko
gehienekoaren ondoan dagoen lehenengo gutxienekoaren
posizioan dagoen erdiko
gehienekoaren ondoan dagoen lehenengo gutxienekoaren
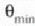 angelua kalkulatu behar da
(N zirrikitu daudela onartuko da). Fasean dauden N iturrik eragindako lehenengo gutxienekoaren
angeluaren kalkulua a = N d zabalera duen zirrikitu bakarrak eragincako lehenengo gutxienekoaren
angeluaren berdina da. Beraz, gutxienekoa ondorengo baldintza hau betetzen duen
angelua kalkulatu behar da
(N zirrikitu daudela onartuko da). Fasean dauden N iturrik eragindako lehenengo gutxienekoaren
angeluaren kalkulua a = N d zabalera duen zirrikitu bakarrak eragincako lehenengo gutxienekoaren
angeluaren berdina da. Beraz, gutxienekoa ondorengo baldintza hau betetzen duen
 angeluarekin gertatuko da:
angeluarekin gertatuko da:
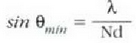
Angelu txikien kasuan,
 gaiaren ordez
gaiaren ordez
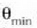 jar daiteke. Erdiko gehienekoa
jar daiteke. Erdiko gehienekoa
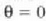 angeluan olagoenez,
erdiko gehieneko horren eta lehenengo gutxienekoaren arteko
angeluan olagoenez,
erdiko gehieneko horren eta lehenengo gutxienekoaren arteko
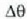 tarte angeluarra gutxi
gorabehera hauxe izango da:
tarte angeluarra gutxi
gorabehera hauxe izango da:
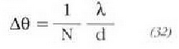
Angelu zabalera" hori 1/N faktorearen eta ordena desberdineko (31. ekuazioko ni desberdinak) tarte angeluarraren arteko biderkaketa ola gutxi gorabehera, angelu txikietarako angelu tarte hori 1/dren berdina baita.
32. irudian, iturri batetik datorren argia aztertzeko difrakzio sare bat erabiltzen duen espektroskopio arrunta ikus daiteke. Iturria, oro har, gas baten atomoak dituen hodia izaten da, helioa edo sodio lurrina adibidez.

Hodiko atomoak kitzikatzen dira, hodiari aplikatzen zaion goi-tentsioak elektroiak azeleratzen dituelako eta
elektroiek atomoen kontra talka egiten dutelako. Iturriak igorriko duen argia ez da espektro jarrai
batez osatua izango, baizik eta hodian dauden atomoen bereizgarri diren zenbait uhin luzerez.
Iturritik datorren argiak zirrikitu estu bat zeharkatuko du, eta lente konbergente baten bitartez,
sorta paralelo bilakatuko da. Lentetik irtengo den sorta paralelo horrek sarea joko du. Irudia urrun
dagoen pantaila batean ikusi beharrean, saretik datorren argi paraleloa sistema optiko egoki baten bidez
fokatuko da, eta horrela hor bertan ikusi ahal izango da aipatutako irudia. Tresna optiko hori euskarri
birakari baten gainean jartzen da; euskarria mailakatua da
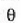 angelua neurtu ahal izateko
angelua neurtu ahal izateko
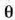 angelua baliogabea denean,
erdiko gehienekoa ikusiko da uhin luzera guztietarako.
Iturriak
angelua baliogabea denean,
erdiko gehienekoa ikusiko da uhin luzera guztietarako.
Iturriak 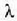 uhin luzerako argia
igortzen badu, lehenengo gehieneko interferentzia (31) ekuazioan m = 1 eginez lortuko den angelurako
aztertuko da. Oro har, iturriak uhin luzera bat baino gehiago igorriko duenez, espektroskopioan
azalduko den gehieneko lehen interferentzien kopurua uhin luzera desberdinen kopuruaren berclina izango da.
Gauza bera gertatuko da, jakina, beste ordena guztietarako. Espektroskopioan ikus daitekeen irudi
(lerroak izango dira) bakoitzari, espektro lerroa edo marra esaten zaio.
Hala,
uhin luzerako argia
igortzen badu, lehenengo gehieneko interferentzia (31) ekuazioan m = 1 eginez lortuko den angelurako
aztertuko da. Oro har, iturriak uhin luzera bat baino gehiago igorriko duenez, espektroskopioan
azalduko den gehieneko lehen interferentzien kopurua uhin luzera desberdinen kopuruaren berclina izango da.
Gauza bera gertatuko da, jakina, beste ordena guztietarako. Espektroskopioan ikus daitekeen irudi
(lerroak izango dira) bakoitzari, espektro lerroa edo marra esaten zaio.
Hala, 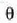 angelua neurtuz gero,
eta sareko zirrikituen arteko d tartea ezagutuz gero, iturriak igorritako uhin luzerak lor daitezke.
angelua neurtuz gero,
eta sareko zirrikituen arteko d tartea ezagutuz gero, iturriak igorritako uhin luzerak lor daitezke.
Era horretako espektroskopioek ia balio bereko bi uhin luzerari dagokien argia neurtzeko ahalmena dute.
Adibidez, sodioaren espektroan nabarmentzen diren kolore horiko bi lerroen uhin luzeren balioak 589.00
eta 589.59 nm dira. Dakigunez, bi lerro horiek bereizita ikusiko dira, horien gehieneko interferentziak
elkarren gainka jartzen ez badira. Lehen aipatutako Rayleigh bereizmen irizpidearen arabera, uhin luzera
horiek bereizita egongo dira, horien gehieneko interferentzien arteko tarte angeluarra, gehieneko
interferentzia baten eta lehenengo gutxieneko interferentziaren arteko tarte angeluarra baino handiagoa bada.
Angelu txikiak hartuko dira 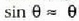 hurbilketa
aintzat hartzeko.
hurbilketa
aintzat hartzeko. 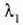 uhin luzerari
dagokion m ordenako gehienekoaren
uhin luzerari
dagokion m ordenako gehienekoaren 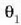 angelua
hau izango da (31. formula):
angelua
hau izango da (31. formula):
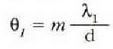
eta 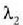 uhin luzerako argiaren kasuan:
uhin luzerako argiaren kasuan:
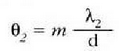
Hala, gehieneko horien arteko tarte angeluarra hau izango da:
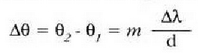
Uhin luzera horiek Rayleigh irizpidearen arabera bereizita ikusi ahal izango dira, azken tarte angeluar hori uhin luzera horietako bati dagozkion gehienekoaren eta gutxienekoaren arteko tarte angeluarraren (32. ekuazioak emandakoa) berdina bada, alegia,
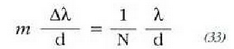
betetzen bada. Difrakzio sare baten bereizmen ahalmena honela definituko da:
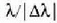 ,
non
,
non 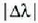 bi uhin luzera anitzekoren
arteko diferentzia den, eta uhin luzera biek k-ren berdinak izan behar dute gutxi gorabehera. Hortaz,
(33) ekuazioaren arabera, R bereizmen ahalmena honako hau izango da:
bi uhin luzera anitzekoren
arteko diferentzia den, eta uhin luzera biek k-ren berdinak izan behar dute gutxi gorabehera. Hortaz,
(33) ekuazioaren arabera, R bereizmen ahalmena honako hau izango da:
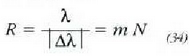
Azpimarratzekoa da, emaitza hori angelu txikien hurbilketa kontuan hartuz lortu bada ere, guztiz orokorra dela, angeluen balioak edonolakoak izanda ere.
(34) adierazpena erabiliaz sodioaren bi lerro horiak bereizteko behar den bereizmen ahalmena lor daiteke:
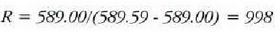
Nola ulertu behar da, baina, emaitza hori? Honela: sodioaren bi lerro horiak lehenengo ordenean (m = 1) bereizteko asmotan, argiak erasotzen duen gunean 1000 zirrikitu gutxi gorabehera dituen sarea beharko da. Beste ordena guztietarako ere, berehala egin daiteke kalkulua.
Newton, Isaac (Sir)
(1642-1727)
Fisikari eta matematikari ingelesa. Binomioaren teorema aurkitu zuen, kalkuluak asmatu zituen eta mekanika, optika eta grabitazio arloetako teoriak garatu zituen.
Newton, Galileo hil zen urte berean jaio zen, denbora baino lehen, aita hil eta hiru hilabetera. Lincolnshireko Woolsthorpe Manor etxaldeko nagusia zuen aita. Ama berriro ezkondu zenean Woolsthorpen geratu zen Isaac txikia, amonaren eta osabaren zaintzapean eta azken hau berehala ohartu zen ilobaren talentuaz. Newtonek Granthamgo eskolan egin zituen lehen ikasketak, eta bi urtez Woolsthorpen baserri lanetan jardun ondoren, Cambridgeko Trinity Collegera bidali zuten, 1 661ean. l a berrogei urte emango zituen han. Badirudi Newton gaztetan, gaur egun «hippy» deituko geniokeen itxurako mutila zela. Bere garaiko ikasle batek hara zer zioen: 'ikastetxean afaltzen zuen askotan... galtzerdiak erorita eta ilea ia orraztu gabe'. 46 urte zituela Knellerrek egin zion erretratuan, artean arropa ez formalez jantzita eta oso ile luzearekin agertzen da.
Newtonen matematikako irakaslea Isaac Barrow izan zen (1630-77). 1 665ean, Londresko Izurri Handia zela eta, Woolsthorpeko bere jaiotetxe bakartura itzuli behar izan zuen. Han landu zituen gerora halako ospea emango zioten ideia asko, Newtonen 'mirarizko urtea' deitu izan zaion hartan. Hona zer idatzi zuen berak 1716an:
1665 urtearen hasieran, serieak hurbiltzeko metodoa eta binomio baten berretzailea serietara laburtzeko legea aurkitu nituen (binomioaren teorema). Urte bereko maiatzean, Gregory eta Sulziusen tangenteen metodoa aurkitu nuen eta azaroan, fluxioen zuzeneko metodoa (kalkulu diferentzialaren elementuak). Hurrengo urteko urtarrilean, koloreen teoria garatu nuen eta maiatzean, fluxioen atzerako metodoa (kalkulu integrala). Urte berean, grabitateaz pentsatzen hasi nintzen, ilargiaren ibilbidea buruan nuela... eta ilargiari bere orbitan eusteko behar den indarra lur azaleko grabitazio indarrararekin alderatu nuen... Hau guztia, 1665 eta 1666 urteetan izan zen, urte horiek izan baitziren nire bizitzako onenak asmaketarako. Urte haietan adina ez naiz geroztik arduratu Matematikaz eta Filosofiaz.' Trinity Collegera itzuli zenean, unibertsitateko kontseilukide hautatu zuten (1667), eta 1 669an, 26 urte zituela, Isaac Barrowren lekua hartu zuen matematikako katedran. 1 672an Royal Societyko kide egin zuten. 1 669tik 76ra aurkeztu zituen optikako bere emaitza gehienak eta eztabaida handitan sartua ibili zen. 1 679an Hookeri gutunak idazten hasi zen, berriro dinamikaz arduratu zen eta Keplerrek aurkitutako planeten mugimendu eliptikoaren arazoa ebatzi zuen. Halleyk ikustaldi bat egin zion Newtoni 1684an eta dinamikari buruzko lan bat idatz zezan konbentzitu zuen. Handik 18 hilabetera liburua idatzita zegoen: Philosophiae naturalis principia mathematica (1687). Zientziaren arloan inoiz idatzi den liburu garrantzizkoena eta eraginkorrena jotzen dute zenbaitzuk.
Data horretatik aurrera Newton ez zen ia matematikaz arduratu eta haren tokia teologiak (badirudi antitrinitarioa izan zela, non ikasi zuen kontuan hartuta gezurra badirudi ere) eta politikak hartu zuten. Alkimiari ere denbora asko eskaini zion garaitsu hartan baina ez zuen emaitzarik lortu. 1 687an kantzelariordeari laguntzera joan zen Londresa, unibertsitatea defenditzera James Ilaren ez legezko larderien aurka. 1692an, Newton beraren hitzetan 'burua galdu zuen'. Segur aski depresio aldi larriren bat pasa zuen.
Behin sendatu zenean Londresa joan zen bizitzera, eta han, Charles Montagueren adiskidantzari esker (Royal Societyko kide eta Halifaxko lehen kondea zen), 1696an, Diru Etxeko Zaindari lehenik, eta gero, 1 698an, Nagusi izendatu zuten (Master of the Mint) eta trebetasun handiz diruaren erreforma burutu zuen. Hori zela eta, Sir izendatu zuten 1705ean. Londresen bizi zela iloba gazte bat hartu zuen etxezaintzarako. Catherine Barton zuen izena eta polita, xarmangarria eta buruz azkarra omen zen. Charles Montagueren maitale izan zen. Newtonen Diru Etxeko zereginen artean, txanpongintza ikuskatzea zegoen, eta bitxia dirudien arren, baita txanpon faltsifikatzaileak harrapatzea, itauntzea eta auzitaratzea ere. 1701ean, bertan behera utzi zituen Trinity Collegeko katedra eta kontseilukidetza, baina Royal Societyko lehendakari izan zen 1703tik hil zen arte. Parlamentuko kide ere aukeratu zuten (Whig alderdikoa, Partidu Liberalekoa, alegia) unibertsitatetik, baina ez zuen ezer askorik egin politikagintzan.
Azken 20 urteetan, eztabaida garratzak izan zituen Flamsteed eta Leibnizekin zientzia aurkikuntzetako aitzindaritzari buruz eta Newtonek bere alderdi gupidagabeena eta obsesiboena erakutsi zuen eztabaida haietan. Gaixotasun mingarri baten ondoren (behazun-harriak izan zituen) 1 727an hil zen eta Westminsterreko Abatetxean dago hobiratuta. Osasun onekoa izan zen, hortz bat besterik ez zuen falta hil zenean, eta zahartuta ere, ez zuen betaurreko beharrik izan. Agi danean, ez zuen amodiorik edo zientziaz kanpoko beste bizitzarik izan. Poesiari buruz zer iritzi zuen galdetuta, hara zer erantzun zuen: 'Barrowren hitzekin erantzungo dizut; hark esaten zuen zentzugabekeria irudimentsu bat baizik ez zela poesia.
Newtonek mekanikan egindako aurkikuntzek nagusitza osoa ezarri zuten mendebaleko zientzia munduan eta dinamikaren oinarrizko hiru legeak formulatu zituen: (1) geldirik dagoen edo higidura uniformea duen gorputz batek, ez du aldatuko bere gelditasuna edo higitze egoera, kanpoko indar baten eraginik ez duen bitartean; (2) gorputz baten gainean egiten den indarra, gorputz horren masa bider hartzen duen azelerazioaren berdina da; (3) gorputz batek beste bati indar bat egiten dionean, neurri bera baina aurkako noranzkoa duen indarra egiten dio bigarren gorputzak lehenari. Horietan oinarrituta azaldu zituen Newtonek zatikien talka, erortzen ari ziren gorputzei buruz Galileok lortutako emaitzak, Keplerrek planeten mugimenduari buruz adierazitako hiru legeak, ilargiaren eta lurraren mugimenduak eta itsasaldiak. Dedukzioak kalkuluak erabiliz atera zituen, baina geometria bidez ere frogatu zituen Principia liburuan, bere garaiko irakurleei argiago azaltzearren.
Newtonek garrantzi handiko beste tratatu bat ere argitaratu zuen 1 704an: Opticks zuen izena eta argiaren portaera deskribatzen zen bertan. Bere esperimentuetan oinarritua zegoen eta argiaren teoria korpuskularra proposatu zuen, baina aldizkakotasun ideiak erantsita (Hooke eta Huygenen uhinen teorian ez bezala). Hark asmatutako ispilu eta lente konbinazioei esker, gero Newtonen teleskopioa deitu zitzaiona egin zuten.
Newtonek eragin ikaragarria izan zuen zientziaren eta pentsamenduaren munduan. Matematikari gisa berak asmatu zituen binomioaren teorema (1676) eta kalkulua. Azken hau eta grabitazio lege unibertsalaren aurkikuntza izan ziren, hain zuzen, bere lorpen handienak. Haren lanari esker nagusitu zen metodo zientifikoa, eta beste norabide bat eman zion fisikari, adierazpen matematikoen bidez azaldu baitzituen gertakari fisikoak.
Hona zer idatzi zuen Einsteinek Newtoni buruz: Izadia liburu ireki bat zen harentzat, eta nekerik gabe irakurtzen zuen... Pertsona bakar batean konbinatu ziren, esperimentugilea, teoria idazlea, mekanikaria, eta azaltzaile argia. Gure aurrean ikusten dugu, indartsu, seguru eta bakarrik. Haren sorkuntzarako etorria eta doitasun harrigarria begien bistakoak dira.' Eta hara zer zioen Newton berak, zahartuta gero, bere bizitzaz: 'Ez dakit munduak nola ikusten nauen, baina nire ikuspegitik, hondartzan jolasean ibili den mutiko bat bezala ikusten dut neure burua, lehendabizi harri edo maskor bitxiren bat aurkitu, eta gero beste baten bila saiatzen, egiaren ozeano handi eta ezezaguna nire aurrean nuela.'
Fresnel, Augustin Jean
(1788-1827)
Frantses fisikaria. Argiaren uhinen teoria azaldu zuen.
Optika lanetan aitzindari izan zen eta, Thomas Younge-en teorietan oinarri hartuta, argi uhinen teoria azaldu zuen. Matematikaren eta tresnen bidezko esperimentuen bidez argiaren uhinen teoria aztertu zuen, eta argiaren uhinak zeharkako dardarak eginez zabaltzen direla frogatu zuen. Lante konposatua asmatu zuen errefrakzio gainaldearen ordez erabili ahal izateko, eta lente mailakatuaren proiektorea egin zuen. Argi polarizatuaren interferentzien legeak ikertu zituen Fran4ois Aragorekin. Biribileko argi polarizatua lortu zuen eta lente konposatuen erabilera bultzatu zuen itsas-argietarako batez ere. Ingeniari lanetan aritu zen zenbait urtez, eta 1815ean Eskola Politeknikoko irakasle izendatu zuten. Frantziako Zientzietako Akademiako kide izan zen 1 823an, eta 1 825ean Britainiar Errege Elkartekoa. Argiaren difrakzioa ere aztertu zuen.
Fresnelen lenteak biribil zentrukideen kristal zerrendez osatutako lenteak dira, bakoitzak lente soil bat du eta gainalde lau batean elkarren ondoan behar bezala jarrita, argitze motzak ematen ditu. Batez ere itsas-argietan eta mikroskopioetan erabiltzen dira Fresnelen lenteak, argi izpien sorta estu eta indartsua behar b aitute. l a ezinezkoa litzateke lente horiek kristal gotor biribil bakarra erabilita egitea, lodiegia eta astunegia bailitzateke. Fresnelen lenteek lente zati txiki landuak erabiltzen ditu, eta zati guztiak elkartuz lente konposatua osatzen dute.
Fraunhofer, Jose von.
(1787-1826)
Alemaniar fisikaria eta optikoa: eguzki espektruaren marra ilunak aurkitu zituen (Frauenhofer-en marrak).
Aprendiz aritu zen ispiluak egiten eta lenteak garbitzen zituen lantegi batean Munichen. Urteen buruan lantegi hartako zuzendari izan zen. Aprendiz urteak oso gogorrak izan zituen; behin, lantegian istripu bat izan zen eta ispilu pila baten azpian gelditu zen, baina bizirik irten zen. Gertaera hura ospatzeko diru saria eman zioten. Diru harekin fisika ikerketak egiten hasi zen. 1 823an Bavariako Zientzia Akademiako Fisika Museoko zuzendari egin zuten; handik hiru urtera hil zen tuberkulosiak jota.
Argiaren difrakzioa aurkitu zuen eta izarren espektru sailkapena finkatzeko erabili zuen. Fraunhoferen marrak eguzkiaren fotosferaren espektruan dauden xurgapen marrak dira. Fraunhofer-ek 1814. urtean aztertu zituen. Lerro horiek elementu kimikoen igorpen espektruetan azaltzen diren marrekin bat egiten dute kokaeran. Lerrook aztertuz Eguzkiaren atmosferaren osaerari buruzko informazio lor daiteke.
Young, Thomas.
(Milverton, 1773 - Londres, 1829)
Britainiar sendagile, fisikari eta egiptologoa. Jakintza arlo asko landu zituen. Gaztetan hizkuntzak ikasi zituen: grekera, latina, alemaniera, arabiera eta pertsiera, besteak beste. Gaztetan ere, maisu baten laguntzaz, teleskopiak egiten ikasten aritu zen. 1 792an medikuntza ikasketak hasi zituen Londresen. Lehenengo ikasle urtean begiaren fisikari buruzko lan bat egin zuen, eta egokitzea (foku aldatzea) lentearen makurdura aldatzearen ondorio dela frogatu zuen esperimentu bidez. Astigmatismoa aztertu zuen eta 1801ean giza ikusmenaren hiru koloreei buruzko teoria azaldu zuen. Ez fisikari ez unibertsitateko irakasle gisa ez zuen nonbait arrakasta handirik izan, "burua beste nonbait zuelako beti", bere lagun batek zioenez. 1 802an fisikako interpretazioa eman zion Hookeren legearen konstanteari, eta handik aurrera Youngen modulua esan zaio delako konstante horri. Nolanahi ere, bere aurkikuntzarik aipagarriena argiaren uhin teoria izan zen. 1800-1804 bitartean teoria hori azaltzen jardun zuen, nola uhinek bata bestearen gainean jartzen direnean interferentziak sortzen dituzten esperimentu bidez frogatzen. 1814tik aurrera buru belarri hasi zen mediku lanean, eta baita egiptologiako lanak egiten ere, antzinako Egiptoko idazketa sistema argitzen laguntzen.
Galileo (Galilei)
(1564)
Fisikari eta astronomo italiarra: Jupiterren ilargiak eta gorputzek erortzean betetzen dituzten legeak aurkitu zituen.
Pisan jaio zen. Aita musikaria zuen eta medikuntza ikasten hasi zen, baina matematikak eta fisikak erakartzenago zuten. 25 urte zituela, oso gutxi ordaintzen bazioten ere, matematika irakasle hasi zen Pisan. 1591 n Paduara joan zen bizitzera, eta geroago Florentziara. Ez zen ezkondu, baina 35 urte zituela Veneziako Marina Gambarekin bizitu zen eta bi alaba eta seme bat izan zituzten. 161Oean, Galileo Florentziara bizitzera joan zenean, ez zuen Marina eraman eta hura berehalaxe ezkondu zen.
Nahiz eta teleskopioa ez zuen berak asmatu, hobekuntza handiak egin zizkion, eta bera izan zen arrakasta handiz lehenengo erabili zuena. Galileoren berrikuntza zera izan zen: objetibo gisa lente estutzaile bat, eta begiaren aldetik lente zabaltzaile bat erabiltzea. 1610ean, ilargiko mendiak, Jupiterren inguruko lau sateliteak eta begi hutsez ikusteko argi ahulegia duten izar asko ikusi zituen lehendabiziko aldiz. Egindako aurkikuntzak, Sidereus nuncius (1610) liburuan argitaratu zituen eta ospe handia eman zioten. Orduan aurkitu zituen Artizarraren faseak, Saturnoren egitura konposatua (nahiz eta ez zen gai izan uztaiak ikusteko: planeta hirukoitz baten gisa ikusten zuen) eta eguzkiko orbanak. Zeruko gorputzak (eguzkia, ilargia eta izarrak) ez zebiltzala lurraren inguruan biraka esan zuenean, eta agerian aldeztu zuenean Kopernikoren teoria (eguzkiaren inguruan zebiltzala planetak, eta lurra horien artean) elizarekin arazo larriak izan zituen. 1632an Dialogo sopra i due massimi sistemi del mondo, tolemaico e copernicano izeneko liburua argitaratu zuen. Liburu horretan, Kopernikoren teoria diplomaziaz aldezten saitu zen, elizako agintariek ulertuko ziotelakoan, baina ideia berriegiak ziren, agi danean, elizak bat-batean onartzeko. Hurrengo urtean Inkisizioak auzitara eraman zuen, eta tortura aretoa erakutsi ondoren, esandakoak ukatzera behartu zuten. Azkenean, bizi zen artean etxean preso egotera zigortu zuten, 69 urte zituela.
Astronomiaz kanpo egin zituen aurkikuntzen artean penduluaren isokronismoa dago (kulunkak luzera berekoak dira, laburrak direnean), eta esan behar da, medikuntzako ikaslea zela, bere pultsuaren bitartez egin zituela ondorio horretara heldu ahal izateko egin beharreko denbora neurketak. Baita ere aurkitu zuen, erortzen ari den gorputzaren lastertasunak ez duela zer ikusirik gorputzaren pisuarekin. Azken aurkikuntza hau, plano aldapetan behera bolak piririkatuz egindako esperimentuetatik ondorioztatu zuen, eta ez, uste izan den bezala, Pisako dorre makurtutik pisuak erortzen utzita. Mekanikari buruzko lanak Discorso intorno a due nuove scienze (1638) liburuan atera zituen, eta liburu horixe nahikoa litzateke 'fisika matematikoaren aitatzat' hartzeko. (Deskribatu zituen 'bi zientzia berriei' egun, 'materialen erresistentzia' eta 'dinamika' esaten zaie). Newton jaio zen urtean hil zen. Haren lan egiteko modua egungoaren oso antzekoa zen: obserbazioa, esperimentua eta matematiken erabilpena emaitzak lortzeko.
Haren omenez gal deitzen zaio azelerazio banako bati: 10-2 m s-2. Miligala berriz, geofisikan erabiltzen da, eta grabitateari zor zaion azelerazio aldaketa neurtzen du.
Galileo musikari trebea, artista eta idazlea ere bazen, benetako Berpizkundeko gizona, alegia. Munduan inoiz izan diren zientzilari handienen artean dago, eta haren aurkikuntza harrigarriak, nortasun kementsua eta elizarekin izan zituen iskanbilak direla eta, historiako zientzilari erakargarrienetako bat bilakatu da.
Huygens, Christiaan
(1629-95)
Fisikari eta astronomo holandarra: argiaren uhin teoria proposatu zuen; Saturnoren eraztunak aurkitu zituen; penduludun erlojua egin zuen; dinamikaren teoria eta pendulu konposatua landu zituen.
Hagako familia aberats bateko semea zen eta lege ikasketak egin zituen zientzian eta matematiketan murgildu aurretik. Bera izan zen, Newtonen ondoren, 17. mendearen azken aldeko fisikari eraginkorrena. 1 655ean, berak hobetutako teleskopio bat erabiliz, Saturnoren eraztunak diren bezala deskribatzen lehena izan zen. Berak aurkitu zuen Saturnoren satelite handiena ere, Titan deitu zaiona. Kodigo zifratu moduan iragarri zituen Saturnoren eraztunen aurkikuntza eta deskribapena. Hurrengo urtean, gorputz malguen talkaren dinamika arazoa ebatzi zuen. Galileok pendulu bakunaren kulunka aldaketarik gabea zela aurkitu zuen bezala, Huygensek horrela formulatu zuen kulunkak txikiak zirenerako: T=2zr(I/g)1/2 non T=periodoa, l=luzera eta g=grabitateak eragindako azelerazioa diren. Penduludun erlojua diseinatu zuen eta geroago, doitasun handiagoa zuen pendulu konposatua asmatu zuen (arku zikloidal batean mugitzen dena). Fisikak ezin izango zukeen aurrera egin denbora doi neurtzeko tresnarik ez balitz.
Huygensen aurkikuntza handiena hala ere, argiaren uhin teoria izan zen: 1 678an azaldu zuen lehen aldiz. Hala, argiaren islatze eta errefrakzio legeak, eta zenbait mineralen errefrakzio bikoitza azaldu ahal izan zituen. Bestalde, iragarri zuen (eta zuzen iragarri ere), argia mantsoago mugitzen dela dentsitate handiagoko inguruneetan. Newtonek nahiago izan zuen argiaren teoria korpuskularra. 20. mendera arte ez zen jakin bi teoriak izan daitezkeela zuzenak, esperimentazio egoeraren arabera.
Huygensek izar batera (Sirius) dagoen distantzia ere kalkulatu zuen: egiatzat emanez eguzkiaren egungo argi bera duela esandako izarrak, plater opako batean zulo txiki-txiki bat egin eta eguzkiaren argia handik pasarazi zuen Siriusekin bat egin arte. Hala egindako kalkuluak 27664 AUko distantzia eman zion, benetakoaren hemezortziren bat, gutxi gorabehera, eta orduan lortutako hurbilena. Konbentziturik zegoen planetetan izaki biziak daudela eta Jupiter eta Saturnorako ontzigintzari eta beste zenbait tresneriari buruz xehetasunez idatzi zuen.
Michelson, Albert Abraham
(1852-1931)
Estatubatuar fisikaria. Doitasun handiko neurketa metodoak asmatu zituen optikan. Balizko eterra segur aski ez zela existitzen erakutsi zuen.
Strelnon jaio zen (egun Polonian) baina lau urte zituela Estatu Batuetara joan zen bizitzera bere gurasoekin. Hamazazpi urte zituela Annapolisko Itsas Armada Akademian sartu zen (sarrera eskaera egitean Grant lehendakaria ikusi eta gero). Graduatu eta itsasoan ibilaldi bat egin ondoren, fisika eta kimikako instruktore izendatu zuten. Dirudienez, zientziarako interesa areagotu egin zitzaion orduan, eta marinelei argiaren lastertasuna nola neur zitekeen frogatu beharrean aurkitu zenean, neurketa haien doitasuna hobetzeko ahaleginetan hasi zen. Nabaria da neurketaren doitasunaren garrantzia hala fisikan nola nabigazioan, eta Michelson gai izan zen bere bizitza osoan, geroz eta neurketa doiagoak egiteko. Berak asmatutako interferometroan oinarritutako tresna optikoek erabilgarritasun handia izan zuten fisikako zeregin askotan.
1880. hamarraldiaren hasieran, 2 urteko ikasketa baimenaz baliaturik, txango bat egin zuen Europara, eta bere lehen interferometroa Helmholtzen laboratorioan egin zen, A G Bell-ek ordainduta. Tresna hari esker argiaren lastertasuna aldera zitekeen argi sorta bakar batetik bereizitako bi argi izpiren artean.
Lan horren emaitzak eraginak izan zituen balizko eterraren arazoan. Nola uhinek -hots uhinek, edo ur uhinek, esate baterako- "bitarteko" bat behar duten zabalduko badira, jakintsuek uste zuten argiak eta gainerako uhin elektromagnetikoek ere bitarteko bat behar zutela transmititu ahal izateko, eta balizko eter unibertsal, ikusezin eta pisu gabea asmatu zuten horretarako. Baina Michelsonen tresneriari esker Lurrak eterretan zukeen mugimenduak argian sor zezakeen eragina neur zitekeen. Baina ezin izan zen inolako eraginik aurkitu, eta beraz, eterraren existentziaz zalantzak sortu ziren fisikarien artean. 1881ean, Michelsonek armada utzi zuen, eta hurrengo urtean Ohioko Clevelanden fisikako irakasle hasi zen. Optikako neurketak hobetzen jarraitu zuen eta Morleyrekin (kimikako irakaslea) eterraren emaitzarik eza egiaztatu zuen 1 887an. Michelson-Morleyren esperimentu klasikoak -berebiziko garrantzia izan zuen fisikan- sari nazionala irabazarazi zion 1 888an, 'ez soilik aurkitu eta ezarri zuenagatik, baizik eta baita oso zabalduak ziren zenbait uste okerrak zirela erakusteagatik ere'. Arazoa, hala ere, ez zen erabat argitu, harik eta, 1905ean, Einsteinen erlatibitatearen teoriak eterraren alferrikakotasuna erakutsi zuen arte.
Michelsonek aurrera jarraitu zuen bere neurketa esperimentuekin eta metroa argiaren uhin luzeraren bidez neurtzea eta zenbait astronomia arazo ebaztea otu zitzaion (bera izan zen izar baten diametro angeluarra neurtu zuen lehena, Betelgeuse izarrarena, hain zuzen, eta errakuntza-perdoia buruorratz baten parekoa izan zen 1000 miliako distantzia batean). Espektruaren ezaugarri berriak ere aurkitu zituen. Interferometroa erabiliz ilargiak eragindako marea mugimenduak ere neurtu zituen, baina ez itsasoan, baizik eta lehorrean. 1890etik hil zen arte, Txikagon aritu zen lanean. 1 907an, lehenengo Nobel sari estatubatuarra izan zen.