Fisika-Kimika»Fisika - Kimika
4. Dinamika klasikoaren oinarriak
Sarrera
Atal honetan gorputzen mugimenduaren sorburua aztertuko da batetik, eta gorputz batzuek beste batzuen mugimenduan zer eta nolako eragina duten, bestetik. Gorputzak zatikitzat hartuko dira. Bestalde, mugimendua zehazten duten ekuazioak zehatz-mehatz aztertuko dira.
Lehenengo lege esperimentala
Demagun bi zatiki daudela, 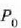 eta
eta 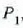 ,
Unibertsoko gainerako zatikietatik oso urrun. Bi zatiki horien arteko elkar
eragina dela-eta, elkar lotzen dituen lerro zuzenaren norabidea eta kontrako
noranzkoa duten azelerazioak dituzte bi zatikiek (4-1 irud.).
Bedi
,
Unibertsoko gainerako zatikietatik oso urrun. Bi zatiki horien arteko elkar
eragina dela-eta, elkar lotzen dituen lerro zuzenaren norabidea eta kontrako
noranzkoa duten azelerazioak dituzte bi zatikiek (4-1 irud.).
Bedi 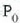 zatikiaren
zatikiaren 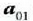 azelerazioa,
azelerazioa, 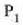 zatikiak eragina dena eta lehen mailako
zatikiak eragina dena eta lehen mailako
4.1 : Bi zatikiren arteko elkar eragina dela-eta (bi zatiki horiek Unibertsoko gainerako zatikietatik oso urrun daudenean), bi zatiki horiek elkar lotzen dituen lerro zuzenaren norabidea eta kontrako noranzkoa duten azelerazioak izango dituzte
inertzia sistema baten barruan dagoena, eta bedi
 zatikiaren
zatikiaren
 azelerazioa,
azelerazioa,
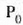 zatikiak eragina.
Esperientziaz frogatu ahal izan da azelerazio horiek sortzen dituzten egoera fisikoak edozein
direla ere (grabitazio erakarpena, erakarpen edo aldaratze elektrikoa, etab.), ondoko hau gertatzen dela beti,
zatikiak eragina.
Esperientziaz frogatu ahal izan da azelerazio horiek sortzen dituzten egoera fisikoak edozein
direla ere (grabitazio erakarpena, erakarpen edo aldaratze elektrikoa, etab.), ondoko hau gertatzen dela beti,

non 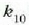 konstante eskalar
positibo bat baita; konstante hori, bestalde, ez da bi zatikien posizio erlatiboaren,
lastertasun erlatiboaren (zatikien lastertasunak txikiak direla argiaren lastertasunaren aldean
hartuko da oinarri), denboraren eta posizioaren mendeko. Minus zeinuak zatiki baten eta bestearen
azelerazioek kontrako noranzkoa dutela adierazten du. Konstanteak aditzera ematen du zatiki guztiek
dutela tasun mekanikoren bat. Hori da, hain zuzen, lehenengo lege esperimentalaren adierazpena.
konstante eskalar
positibo bat baita; konstante hori, bestalde, ez da bi zatikien posizio erlatiboaren,
lastertasun erlatiboaren (zatikien lastertasunak txikiak direla argiaren lastertasunaren aldean
hartuko da oinarri), denboraren eta posizioaren mendeko. Minus zeinuak zatiki baten eta bestearen
azelerazioek kontrako noranzkoa dutela adierazten du. Konstanteak aditzera ematen du zatiki guztiek
dutela tasun mekanikoren bat. Hori da, hain zuzen, lehenengo lege esperimentalaren adierazpena.
Bigarren lege esperimentala. Masaren definizioa
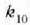 konstantea interpretatzeko hirugarren zatiki bat,
konstantea interpretatzeko hirugarren zatiki bat, 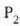 ,
hartuko da, lehenbizi
,
hartuko da, lehenbizi 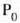 zatikian eragingo duena eta ondoren
zatikian eragingo duena eta ondoren 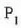 zatikian.
Orduan bi adierazpen, elkarren antzeko, lortuko dira :
zatikian.
Orduan bi adierazpen, elkarren antzeko, lortuko dira :
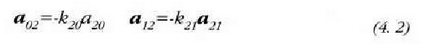
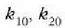 eta
eta 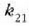 hiru konstanteak elkarren mendeko ez direla onar daiteke, baina esperientziaz frogatu
ahal izan da konstante horien artean harreman hau dagoela:
hiru konstanteak elkarren mendeko ez direla onar daiteke, baina esperientziaz frogatu
ahal izan da konstante horien artean harreman hau dagoela:

Berdintza horren lehenengo osagaia ez da 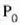 zatikiaren mendeko; horrek adierazten du k konstanteak konstante horien magnitudeen arteko harremanak direla.
zatikiaren mendeko; horrek adierazten du k konstanteak konstante horien magnitudeen arteko harremanak direla.
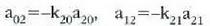 adierazpenaren bigarren berdintzan
adierazpenaren bigarren berdintzan
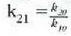 berdintza ordezkatuz gero, beste hau lortzen da:
berdintza ordezkatuz gero, beste hau lortzen da:

Harreman horren arabera, baldin eta 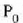 zatikia eredutzat (standard) hartzen bada, edozein zatikiri
zatikia eredutzat (standard) hartzen bada, edozein zatikiri
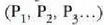 lotu ahal izango zaio konstante bat; konstante horren balioak ez du zatikiaren mendeko izan behar.
lotu ahal izango zaio konstante bat; konstante horren balioak ez du zatikiaren mendeko izan behar.
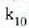 konstanteari horrela esaten zaio:
konstanteari horrela esaten zaio:
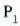 l zatikiaren masa
l zatikiaren masa
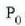 zatikiari buruz, edo
zatikiari buruz, edo 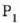 l zatikiaren masa, besterik gabe.
l zatikiaren masa, besterik gabe.
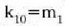 eta
eta 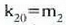 eginez gero -berdintza horietan ez da 0 azpi indizea aipatu, hala komeni baita-,
azken adierazpen hori beste adierazpen hau bilakatuko da:
eginez gero -berdintza horietan ez da 0 azpi indizea aipatu, hala komeni baita-,
azken adierazpen hori beste adierazpen hau bilakatuko da:

Adierazpen hori da bigarren lege esperimentala
Hirugarren lege esperimentala. Indarraren definizioa
Har dezagun berriz ere
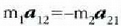 berdintza.
Hipotesiaren arabera, masa eta azelerazioaren arteko biderkadura zatikien posizio erlatiboen,
lastertasun erlatiboen eta denboraren mendekoa da. Mendekotasun funtzional
hori beste bektore funtzio baten bidez adierazten da:
berdintza.
Hipotesiaren arabera, masa eta azelerazioaren arteko biderkadura zatikien posizio erlatiboen,
lastertasun erlatiboen eta denboraren mendekoa da. Mendekotasun funtzional
hori beste bektore funtzio baten bidez adierazten da:
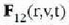 hain zuzen. Funtzio horretan,
hain zuzen. Funtzio horretan, 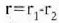 berdintzak adierazten du
berdintzak adierazten du 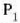 zatikiaren posizio bektorea
zatikiaren posizio bektorea 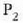 zatikiari buruz.
Behin hori eginda, berdintza hau idatz daiteke:
zatikiari buruz.
Behin hori eginda, berdintza hau idatz daiteke:

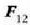 funtzioa horrela defini daiteke:
funtzioa horrela defini daiteke:
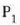 zatikiari eragiten dion indarra
zatikiari eragiten dion indarra 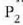 zatikiaren arabera. Berdin-berdin egin daiteke
zatikiaren arabera. Berdin-berdin egin daiteke 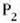 zatikiarekin:
zatikiarekin:

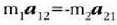 harremanak adierazten du
harremanak adierazten du

betetzen dela, hau da:
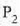 zatikiaren eraginez
zatikiaren eraginez 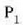 zatikiari eragiten dion indarra eta
zatikiari eragiten dion indarra eta 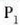 zatikiaren eraginez
zatikiaren eraginez 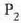 zatikiari eragiten dion indarra berdinak dira, baina kontrako norabidea dute.
Indarra bektore bat da eta azelerazioaren norabide eta noranzko ditu.
zatikiari eragiten dion indarra berdinak dira, baina kontrako norabidea dute.
Indarra bektore bat da eta azelerazioaren norabide eta noranzko ditu.
 adierazpena dagokio hirugarren lege esperimentalari.
adierazpena dagokio hirugarren lege esperimentalari.
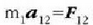 ekuazioa beste era hauetara idatz daiteke:
ekuazioa beste era hauetara idatz daiteke:
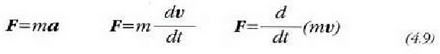
Ekuazio horietan ontzat hartu da m konstante bat dela . Azken adierazpen horri dinamikaren oinarrizko ekuazioa esaten zaio ; indarra masaren eta azelerazioaren arteko biderkaduraren berdina dela adierazten du . Ekuazio hori oinarrizkoa da mugimenduaren inguruko problemak ebazteko
Laugarren lege esperimentala. Gainkatzearen printzipioa.
Bedi 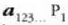 zatikizaren azelerazioa
zatikizaren azelerazioa 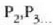 zatikiek lehenengo zatikian batera eragiten dutenean.
Baldin eta
zatikiek lehenengo zatikian batera eragiten dutenean.
Baldin eta 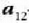 -k
adierazten badu
-k
adierazten badu 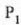 zatikiaren azelerazioa,
zatikiaren azelerazioa, 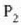 zatikia etab. daudenean bakarrik, hau frogatzen da:
zatikia etab. daudenean bakarrik, hau frogatzen da:
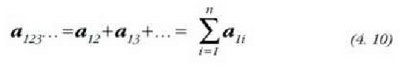
hau da, zenbait zatikiren eraginaren mende dagoen zatiki baten azelerazioa eta zatiki guztiak batera arituko balira sortuko luketen azelerazioen bektore batuketa berdinak dira (gainkatzearen printzipioa). Beste era barera esanda: zatikien arteko eraginek sortzen dituzten azelerazioak askeak dira.
Aurreko ekuazioa bider m l egiten bada, emaitza indarren arabera zehatz daiteke. Emaitza hau da:

Adierazpen horren bidez indarren gainkatzearen legea azaltzen da ; indarrak askeak direla frogatzen du adierazpen horrek . Azken adierazpen horrek, bestalde, laugarren lege esperimentala azaltzen du
Newtonen mugimenduaren legeak
Lau lege esperimental horien oinarrizko edukia eta Newtonen mugimenduaren hiru legeak baliokideak dira. Newtonen legeak honela azaltzen dira:
I. Kanpoko eraginik ez duen zatikiak geldi irauten du edo (erro zuzen bat eratuz egiten duen mugimenduari eusten dio, harik eta kanpoko indar batek egoera hori aldarazten duen arte (inertziaren legea).
II. Zatiki baten azelerazioa zatiki baten gainean egiten den indarraren proportzionala da, eta indarra egiten den norabide berean mugitzen da (dinamikaren oinarrizko legea).
III. Bi zatikik elkarri eragiten diotenean, zatiki baten gainean egiten den indarra beste zatikiaren gainean egiten den indarraren berdina eta kontrakoa da (akzioaren eta erreakzioaren berdintasun legea).
Inertziaren legeak materiaren oinarrizko ezaugarrietako bat azaltzen du.
Zatiki batek indar baten eraginik ez badu, alegia F=0 bada, zatikia edo geldirik dago edo
lastertasun konstanteaz mugitzen da 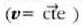 .
F=O denean zatiki batek egiten duen mugimenduari inertzia mugimendua esaten zaio.
Mugimendu horretan zatikiaren azelerazioa baliogabea izaten da (a=0).
.
F=O denean zatiki batek egiten duen mugimenduari inertzia mugimendua esaten zaio.
Mugimendu horretan zatikiaren azelerazioa baliogabea izaten da (a=0).
Inertzia legea betetzen duen erreferentzia sistemari inertzia sistema esaten zaio.
Bigarren legea, lehenengoa bezalaxe, inertzia sistema batentzat bakarrik hartzen da ontzat. Lege horretatik ondorio hau ateratzenda: materia puntu baten inertzia neurria puntu horren masak adierazten du.
(4.9) berdintzaren bidez masa neur daiteke. Esperientziaren arabera, grabitatearen indarraren eraginpean, W, zatiki guztiak libre erortzen direnean, azelerazio berdina dute, g, grabitatearen azelerazioa alegia. Beraz, (4.9) ekuazioaren arabera, hau lortuko da:

Beraz, gorputz baten masa gorputzaren pisua zati grabitatearen azelerazioaren berdina da.
Hirugarren legeak bi materia zatikiren arteko elkar eragin mekanikoaren izaera zehazten du. Materia puntu askeen arteko eragin indarrek ez dute oreka sistema bat osatzen, izan ere, indarrek gorputz desberdinei eragiten baitiete
Banako sistemak
Magnitude mekanikoak neurtzeko hiru neurri banako behar dira. Luzeraren eta denboraren banakoak zinematikan azaltzen dira. Oinarrizko hirugarren banakotzat masa edo indarra hartzen dira. Dena dela, bi banako horiek ezin daitezkeenez arbitrarioak izan, elkarri lotuta egon behar baitute (4.9) berdintasunaren bidez, oinarrizko banakoen bi sistema erabili ahal izango dira.
Lehenengo banako sistema
Sistema mota hauetan oinarrizko banakotzat luzera, masa eta denbora banakoak hartzen dira.
Indarraren banakoa, beraz, banako eratorria da. Sistema mota hauetako bat Nazioarteko
Banako Sistema (NBS) da. Sistema horretan, oinarrizko banakoak hauek dira: metroa (m), kilogramo masa (kg) eta segundoa (s).
Indar banakoa newtona da (N): kilo bat masari 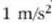 azelerazioa eragiten dion indarra.
azelerazioa eragiten dion indarra.
CGS sisteman oinarrizko banakoak zentimetroa (cm), gramo masa (g) eta segundoa (s) dira. Sistema horretan indarra dinatan neurtzen da (dyn). Newtonaren eta dinaren artean harreman hau dago:
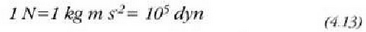
Bigarren banako sistema
Sistema mota hauetan oinarrizko banakotzat hartzen dira luzera, indarra eta denbora.
Masaren banakoa sistema hauetan banako eratorria da. Sistema mota hauen barruan daude:
metroa, kilogramo indarra, segundoa. Sistema hauetan masa banakoa kg
 da, hau da,
kilogramo bateko indarrak
da, hau da,
kilogramo bateko indarrak 
Mekanika klasikoaren mugak
Newtonek azaldu zituen mekanika klasikoaren legeak, ordea, zenbaitetan ez dira egokiak izaten; beraz, aldatu egin behar dira zatikiak argiaren lastertasunaren inguruko lastertasunaz mugitzen direnean, eta eskala txikiko gertakariak azaltzeko erabiltzen direnean, esate baterako fisika atomikoan eta nuklearrean izaten diren gertakariak azaltzeko. Lehenengo kasuan mekanika klasikoaren ordez mekanika erlatibista erabiltzen da, eta bigarrenean, berriz, quantumen mekanika. Hala ere, mekanika erlatibistak eta quantumen mekanikak Newtonen mekanika onartzen dute mugamugan. Dena dela, mekanika klasikoak gertakari fisikoen deskripzio egokia egiten du.
Inertzia indarra
Newtonen legeak, lehen esan bezala, erreferentzia sistema inertzial batean erabil daitezke. Koordenatu sistema ez inertzialetan, ordea, Newtonen legeak aldatu egin behar dira.
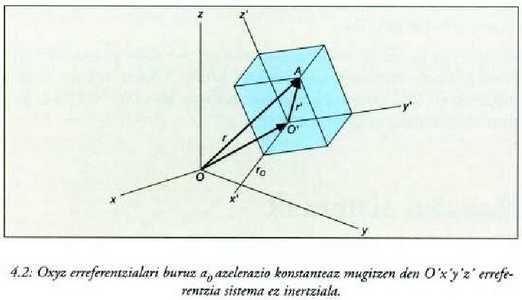
Demagun inertziala ez den O'x'y'z' sistema bat 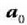 azelerazio konstanteaz mugitzen dela Oxyz erreferentzia sistema inertzialari buruz (4.2 Irud.).
Bedi
azelerazio konstanteaz mugitzen dela Oxyz erreferentzia sistema inertzialari buruz (4.2 Irud.).
Bedi 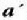 gorputz baten azelerazioa errefentzia sistema ez inertzialari buruz eta a gorputz
horren azelerazioa erreferentzia sistema inertzialean.
Orduan,
gorputz baten azelerazioa errefentzia sistema ez inertzialari buruz eta a gorputz
horren azelerazioa erreferentzia sistema inertzialean.
Orduan, 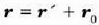 berdintzatik
berdintzatik 
 berdintza ateratzen da. Hortaz:
berdintza ateratzen da. Hortaz:
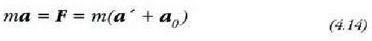
edo bestela,

non

inertzia indarra den. Beraz, gorputzaren masa eta erreferentzia sistema ez-inertzialaren arteko biderkaduraren berdina eta kontrako norabidekoa da inertzia indarra. Inertzia indarrak ez direnez beste gorputzekin izandako eraginen ondorio, erreferentzia sistemako osagai azeleratuaren ondorio baizik, indar horiek ez dute Newtonen hirugarren legea betetzen. Inertzia indarren adierazpena erreferentzia sistema ez inertzialaren mugimenduaren arabera aldatuko da (lerro zuzena, zirkularra, etab.).
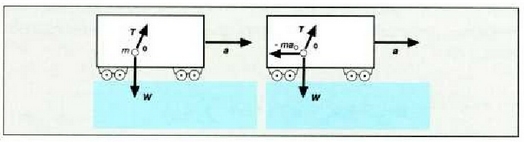
Adibidea. Tren bagoi baten sabaitik m masako
gorputz bat zintzilikatzen da hari batetik, 4.3 irudian ikusten den bezala.
Bagoia eskuinerantz azeleratzen denean, hariak  angeluko desbideratzea jasaten du. Zehaztu bagoiaren azelerazioa:
a) lurrari buruzko koordenatu sistema finko bat erabiliz eta
b) koordenatu sistema azeleratu bat erabiliz.
angeluko desbideratzea jasaten du. Zehaztu bagoiaren azelerazioa:
a) lurrari buruzko koordenatu sistema finko bat erabiliz eta
b) koordenatu sistema azeleratu bat erabiliz.
Ebazpena: a) Lurrari dagokion koordenatu sistema finko bat erabiltzen denean m masa bi indarren eraginpean dago: hariaren T tentsioa eta mg pisua. Beraz,

edo:
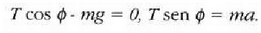
Horrenbestez, bagoiaren azelerazioa 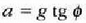 da.
da.
b) Bagoiari dagokion koordenatu sistema finko bat erabiltzen denean, berriz, m masa geldik dago.
Kasu honetan sistemari hariaren T tentsioak, mg pisuak eta
 inertziak eragiten diotenez:
inertziak eragiten diotenez:
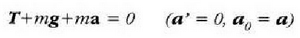
edo:
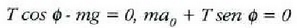
hau da, berriro
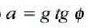
LANA ETA ENERGIA
Oinarrizko lana
Demagun P materia puntu batean indar bat egiten dela, puntuak espazioan duen posizioaren funtzioaF=F (xyz) dela;
bedi dr puntuak izan duen leku aldatzea (4.4 irud). F eta 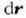 arteko biderkadura eskalarrari esaten zaio dr leku aldatzeari dagokion F indarraren oinarrizko lana,
arteko biderkadura eskalarrari esaten zaio dr leku aldatzeari dagokion F indarraren oinarrizko lana,
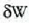 (
( 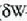 -ren ordez
-ren ordez
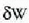 sinboloa erabiltzen da adierazteko
sinboloa erabiltzen da adierazteko
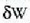 ez dela diferentzial zehatza), hau da:
ez dela diferentzial zehatza), hau da:
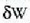
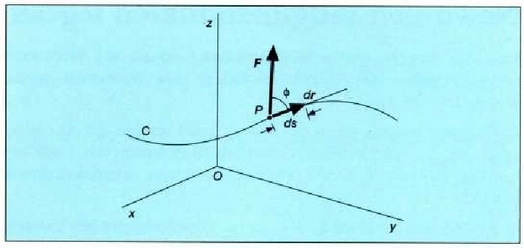
4. 4. F indarraren eta indar horren aplikazio puntuaren dr oinarrizko leku aldatzearen arteko biderkaketa eskalarra eginez gero, indarrak egindako oinarrizko lana lortzen da .
Baldin eta, ds laburduraren bidez adierazten bada kurban neurtutako arkua eta
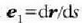 berdintzaren bidez bektore tangente bateratzailea P puntuan, orduan:
berdintzaren bidez bektore tangente bateratzailea P puntuan, orduan:

Baina 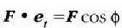 denez gero, non
denez gero, non 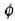 den F eta
den F eta 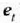 bektoreek osatzen duten angelua, beste ekuazio hau ere lor daiteke:
bektoreek osatzen duten angelua, beste ekuazio hau ere lor daiteke:

Leku aldatzea indarren norabide eta noranzko berean gertatzen bada, orduan,
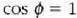 denez gero, hau lortuko da:
denez gero, hau lortuko da:

eta F indarra dr leku aldatzeari buruz zuta bada, orduan,
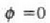 denez gero, berdintza hau lortzen da:
denez gero, berdintza hau lortzen da:

Hau da, indarrak ez du lanik egiten. Azkenik, F eta dr bektoreek angelu zorrotza eratzen badute, lana positiboa izango da, eta angelu kamutsa eratzen badu, berriz, lana negatiboa izango da.
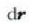 leku aldatze infinitu txikia dt denboran egiten bada, puntu horrek lekuz aldatzean hartzen duen lastertasuna
leku aldatze infinitu txikia dt denboran egiten bada, puntu horrek lekuz aldatzean hartzen duen lastertasuna
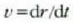 izango da,
eta oinarrizko lanarentzat adierazpen hau lortzen da:
izango da,
eta oinarrizko lanarentzat adierazpen hau lortzen da:
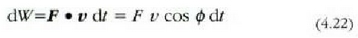
izan ere, indarrak eta lastertasunak eratzen duten angelua eta indarrak eta leku aldatzeak eratzen dutena berdinak dira
Lana kurba batean
Zatikiak C kurba bat eratzen badu 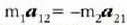 espazioan, leku aldatze osoa
espazioan, leku aldatze osoa 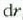 oinarrizko leku aldatze infinituen emaitza bezala har daiteke eta F indarraren lan osoa oinarrizko
lan guztien batuketa bezala, hau da:
oinarrizko leku aldatze infinituen emaitza bezala har daiteke eta F indarraren lan osoa oinarrizko
lan guztien batuketa bezala, hau da:
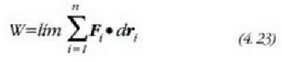
W limitea F indarraren lan osoa da; eta C kurban F indarraren kurba integral baten bidez adierazten da:
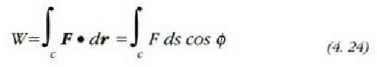
Koordenatu kartesiar lauki zuzenetan lan osoa honela adierazten da:
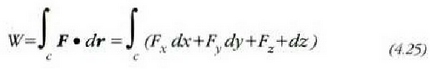
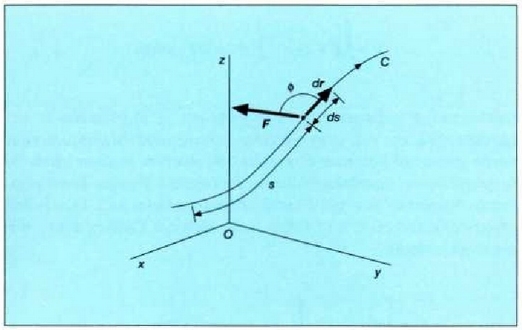
4.5: Indar batek kurba batean egiten duen indarra eta kurba horretan hartutako Oinarrizko lanaren integrala berdinak dira
non 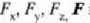 indarren proiekzioak baitira, eta dx, dy, dz, berriz, dr leku aldatze bektorearen proiekzioak.
C jartzen denean integralaren behealdean, integrazioaren bidea adierazten da.
indarren proiekzioak baitira, eta dx, dy, dz, berriz, dr leku aldatze bektorearen proiekzioak.
C jartzen denean integralaren behealdean, integrazioaren bidea adierazten da.
Adibidea.
Helize formako malguki baten luzapenean egindako lana
Esperientziaren arabera malguki bat x
luzeraraino luzatzeko behar den F indarra leku aldaketaren proportzionala da (Hookeren legea),
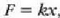 non k
proportzionaltasun konstante bat baita. Horrenbestez:
non k
proportzionaltasun konstante bat baita. Horrenbestez:
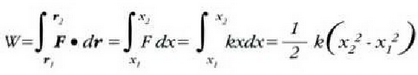
non 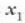 eta
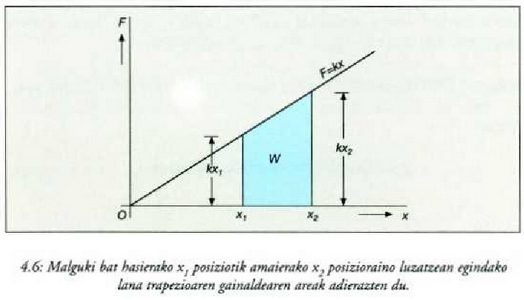
eta 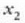 malgukiaren hasierako eta amaierako luzerak diren, hurrenez hurren. 4.6 irudian lan hori
trapezioaren gainaldearen areak adierazten du. Baldin eta
malgukiaren hasierako eta amaierako luzerak diren, hurrenez hurren. 4.6 irudian lan hori
trapezioaren gainaldearen areak adierazten du. Baldin eta
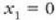 eta
eta 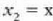 , orduan:
, orduan:
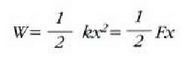
C kurba parametro ekuazioen bidez definitzen bada:
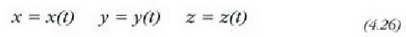
non t, esate baterako, denbora baita, orduan (4.25) ekuazioa era honetara idazten da:
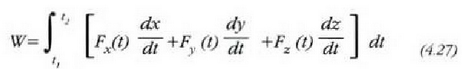
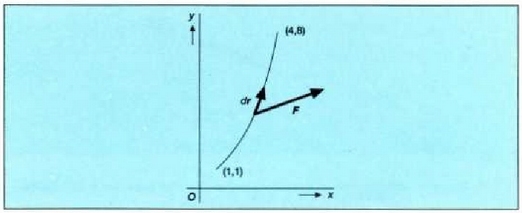
Adibidea. Zatiki bat  kurban zehar mugitzen da
kurban zehar mugitzen da 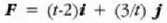 indarraren eraginpean. Zehaztu indar horrek t = 1, t = 2 tartean egindako lana. (4.7 irudia)
indarraren eraginpean. Zehaztu indar horrek t = 1, t = 2 tartean egindako lana. (4.7 irudia)
Ebazpena. (4.27) ekuazioa erabiliz ondoko adierazpena ateratzen da:
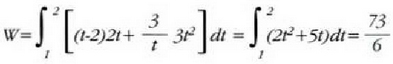
Lan unitatea
Nazioarteko Banako Sisteman lanaren unitatea Newton-metroa da (N-m). Joule esaten zaio ( j ):
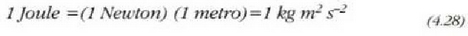
CGS sisteman lanaren unitatea dina-zentimetroa da. Ergio esaten zaio (erg):
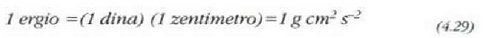
Joulearen eta ergioaren arteko elazioa hau da:
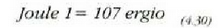
Teknikan, kilogrametroa ere erabiltzen da (kg-m). Kilogrametro bat hau da: kilogramo bateko indarrak, indarraren aplikazio puntua lekuz metro batez aldatzen denean, egiten duen lana. Baina, lkg=981 000 dyn eta lm = 100 cm denez gero:
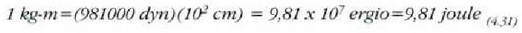
Beraz:
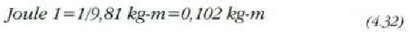
Potentzia
Indar baten lana definitzen denean, ez da kontuan hartzen lan hori egiteko behar den denbora. Hala ere, oinarrizkoa izaten da jakitea F indar batek denbora unitate batean zenbat lan egiten duen.
Baldin eta 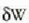 zeinuak adierazten badu F indarrak dt denboran egiten duen lana, potentzia honela lortzen da:
zeinuak adierazten badu F indarrak dt denboran egiten duen lana, potentzia honela lortzen da:

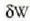 oinarrizko indarren ordez
oinarrizko indarren ordez
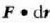 jarriz gero, hau lortzen da:
jarriz gero, hau lortzen da:

edo bestela:
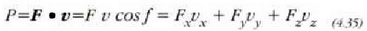
non F aplikazio puntuaren lastertasuna edo indar egiten den zatikiaren lastertasuna baita
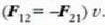 Beraz, potentzia F eta v bektoreen biderkadura eskalarrak neurtzen du eta, oinarrizko lana
bezala, positiboa, negatiboa edo baliogabea izan daiteke, F eta dr bektoreek angelu zorrotza,
kamutsa edo zuzena osatzen duten
Beraz, potentzia F eta v bektoreen biderkadura eskalarrak neurtzen du eta, oinarrizko lana
bezala, positiboa, negatiboa edo baliogabea izan daiteke, F eta dr bektoreek angelu zorrotza,
kamutsa edo zuzena osatzen duten
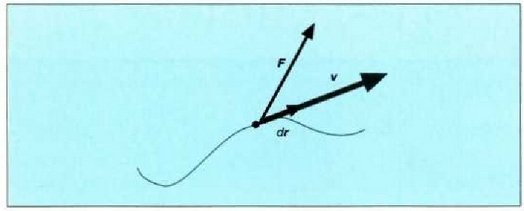
4.8: F indarraren eta indarra aplikatzen den puntuaren v lastertasunaren arteko biderkadura eskalarrak ahalmena ematen du
Potentzia unitatea
SI sisteman potentzia unitatea Joule 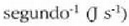 da.
Watt esaten zaio:
da.
Watt esaten zaio:
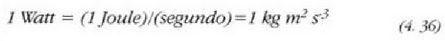
CGS sisteman, potentzia unitatea ergio s  da
da
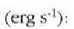
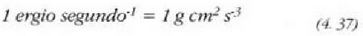
Teknikan, kilowatt 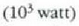 da gehien erabiltzen den banakoa. Zaldiak ere asko erabiltzen dira (CV):
da gehien erabiltzen den banakoa. Zaldiak ere asko erabiltzen dira (CV):
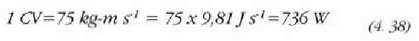
Kilowatt orduko. Ordubetean kilowatt bateko potentiza duen motor batek egiten duen lanari kilowatt orduko esaten zaio (kWh):
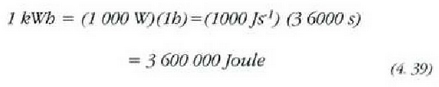
Potentzial energia
Demagun zatiki batean eragiten duen indarra puntuaren posizioaren funtzioa dela, hau da,
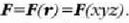 .
Orduan, indar eremua sortzen da. Indarrak egiten duen lana, edozein C ibilbidean puntu bat
.
Orduan, indar eremua sortzen da. Indarrak egiten duen lana, edozein C ibilbidean puntu bat
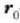 -tik r-ra mugitzen denean, hau da:
-tik r-ra mugitzen denean, hau da:

Oro har, puntuak 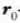 tik r-ra mugitzeko egiten duen ibilbidearen araberakoa da lan hori.
Hala ere, zenbaitetan, F indar eremua hainbestekoa da non integralaren balioa ez baita ibilbidearen mendekoa.
Eremu horiei kontserbatzaile esaten zaie, ere, geroago ikusiko dugun bezala,
horietan energia mekanikoa kontserbatu egiten baita.
tik r-ra mugitzeko egiten duen ibilbidearen araberakoa da lan hori.
Hala ere, zenbaitetan, F indar eremua hainbestekoa da non integralaren balioa ez baita ibilbidearen mendekoa.
Eremu horiei kontserbatzaile esaten zaie, ere, geroago ikusiko dugun bezala,
horietan energia mekanikoa kontserbatu egiten baita.
Indar eremu bat kontserbatzailea da, V(r) =V(x, y, z) funtzio eskalar bat bada berdintza hau betetzen duena:
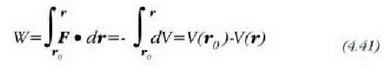
Halakoetan, F indarrak 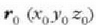 eta r(x, y, z) puntuen artean egindako lana eta V(x, y, z) funtzioaren muturreko bi puntu horien arteko gutxitzea berdinak dira.
Hori hala denean, lanaren balioa ez da integrazioan egindako bidearen mendekoa.
Funtzio horri puntuaren potentzial energia F indar eremuan esaten zaio.
Lana baliogabea da baldin eta C kurba itxia bada, izan ere, halakoetan
eta r(x, y, z) puntuen artean egindako lana eta V(x, y, z) funtzioaren muturreko bi puntu horien arteko gutxitzea berdinak dira.
Hori hala denean, lanaren balioa ez da integrazioan egindako bidearen mendekoa.
Funtzio horri puntuaren potentzial energia F indar eremuan esaten zaio.
Lana baliogabea da baldin eta C kurba itxia bada, izan ere, halakoetan
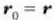 baita, eta orduan:
baita, eta orduan:
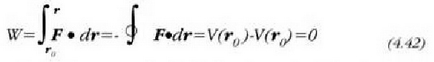
Ekuazio horren arabera,  puntutik r puntura joateko egindakolana ez da ibilbidearen mendekoa. Esate baterako, demagun
puntutik r puntura joateko egindakolana ez da ibilbidearen mendekoa. Esate baterako, demagun
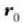 etar puntuen artean bi ibilbide daudela,
I eta 11, orduan (4.9. irud)aurreko ekuazioaren arabera:
etar puntuen artean bi ibilbide daudela,
I eta 11, orduan (4.9. irud)aurreko ekuazioaren arabera:
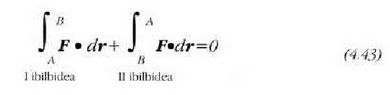
edo:
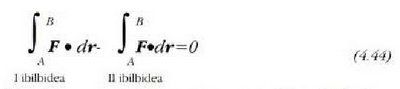
hau da, egindako lana ez da integrazioan egindako ibilbidearen mendeko.
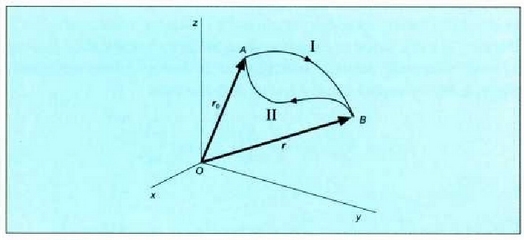
4.9 . A eta B puntuen arteko integrazioa egiteko bi bide desberdin . Indar eremu kontserbatzailean egindako lana ez da integrazioan egindako ibilbidearen mendekoa
Adibidea. Kalkulatu 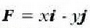 indarrak (0,0) puntutik (1,1) puntura bitartean egindako lana ondoko kasu hauetan:
a) indarraren aplikazio puntuak egindako ibilbidea y = x lerro zuzena denean;
b) indarraren aplikazio puntuak egindako ibilbidea
indarrak (0,0) puntutik (1,1) puntura bitartean egindako lana ondoko kasu hauetan:
a) indarraren aplikazio puntuak egindako ibilbidea y = x lerro zuzena denean;
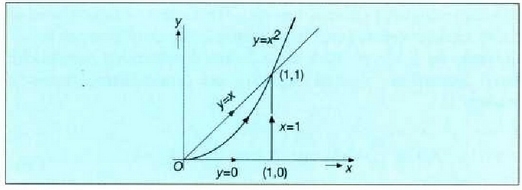
b) indarraren aplikazio puntuak egindako ibilbidea 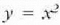 parabola denean, eta c) indarraren aplikazio puntuak egindako ibilbidea x = 0 puntutik x = 1
puntura bitarteko x-en ardatza, eta x= 1 lerroa y = 0 puntutik -v = 1 puntura denean (4.10 irud.).
parabola denean, eta c) indarraren aplikazio puntuak egindako ibilbidea x = 0 puntutik x = 1
puntura bitarteko x-en ardatza, eta x= 1 lerroa y = 0 puntutik -v = 1 puntura denean (4.10 irud.).
Ebazpena: Bedi 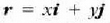 ibilbidearen puntu bat, edozein.
F = 0 eta dz = 0 denez, orduan
ibilbidearen puntu bat, edozein.
F = 0 eta dz = 0 denez, orduan 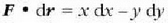 da.
da.
a) y = x ibilbidean zehar dy = dx da. Beraz:
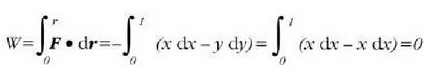
b) 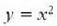
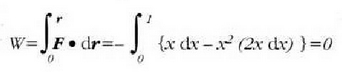
c) y = 0 lerroan zehar dy = 0 da, eta x = 1 lerroan zehar dx = 0. Beraz:
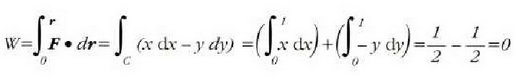
Ikusten denez indarrak egindako lana independentea da hasierako puntutik amaierako puntura joateko egindako ibilbideari buruz.
Indar eremu kontserbatzaileak
Grabitazio eremua
indar eremu kontserbatzailearen adibide arruntena grabitazio eremua da. Grabitatea bada zatikiari eragiten dion indar bakarra, eta z ardatza bertikala eta goranzko norabidekoa bada (4.11 irud.), orduan:
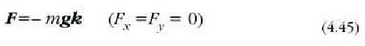
eta

Beraz, 4.41 ekuazioaren arabera, hau lortuko da.
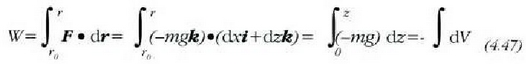
edo,
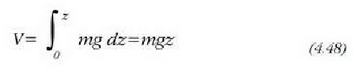
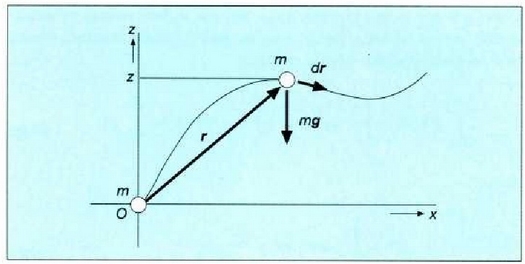
4. 11 : Grabitate indarraren lana indarraren modulua bider indarraren aplikazio puntuaren goitik beherako leku aldaketa da
non V ahalmen energia zero dela hartu baita abiapuntutzat, z=0 bete dadin. Beraz, materia puntu batek grabitazio eremuan duen energia potentziala, konstante arbitrario gehigarri bat salbu, z-ren mendeko baizik ez da, eta ekuazio honen bidez adierazten da:

Kontuan hartzekoa da edozein indar konstanteren (F=c=cte) eremua kontserbatzailea dela.
Indar zentral baten eremua
Bada beste eremu kontserbatzaile garrantzi handiko bat, indarzentralarena hain zuzen, hau da, O puntu finko batetik -indar zentroa- igarotzen den eragin lerroaren indar eremua, zeinaren magnitudea P aplikazio puntuen eta 0 zentroaren arteko distantziaren mendeko baizik ez den (4.12 irud.). Koordenatuen sorburutzat 0 puntua hartuz gero:
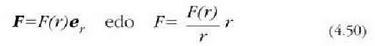
non 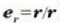 bektore bateratzailea baita. Kontuan hartu behar da ez dela hipotesirik egiten F(r) formari buruz,
F-k eta r-k noranzko bera dutelakoa salbu. F eta r noranzko berekoak badira, F indarrak koordenatuen sorburutik,
O, eragiten den aldaratzea adierazten (tu; F eta r kontrako noranzkoak badira, aldiz,
indarra erakarpenezkoa izango da, eta O erakarpenaren zentroa.
bektore bateratzailea baita. Kontuan hartu behar da ez dela hipotesirik egiten F(r) formari buruz,
F-k eta r-k noranzko bera dutelakoa salbu. F eta r noranzko berekoak badira, F indarrak koordenatuen sorburutik,
O, eragiten den aldaratzea adierazten (tu; F eta r kontrako noranzkoak badira, aldiz,
indarra erakarpenezkoa izango da, eta O erakarpenaren zentroa.
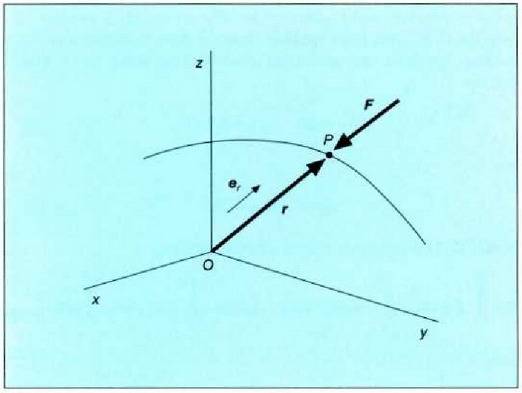
4.12: Beti puntu finko batetik -indar zentroa- igarotzen den eragin lerroa dagokion indar baten eremua eremu kontserbatzailea da
a) 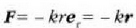 betetzen bada, hau da, indar zentrala r distantziaren proportzionala bada, malguki bati
lotutako materia puntu batean gertatzen den bezala, orduan:
betetzen bada, hau da, indar zentrala r distantziaren proportzionala bada, malguki bati
lotutako materia puntu batean gertatzen den bezala, orduan:
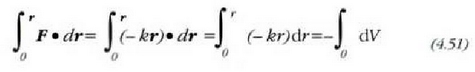
Beraz,

non r=O-ren lekuan 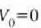 jarri den.
jarri den.
b)  bada, hau da,
indarra distantziaren koadroari buruzko alderantziz proportzionala bada, orduan:
bada, hau da,
indarra distantziaren koadroari buruzko alderantziz proportzionala bada, orduan:
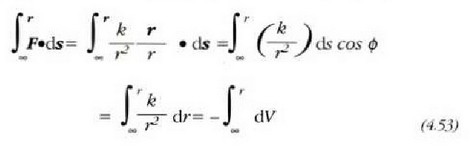
Beraz,
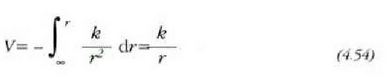
non 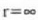 berdintzarako ontzat
hartu den V ahalmen energia zero dela.
berdintzarako ontzat
hartu den V ahalmen energia zero dela.
 ekuazioan
ekuazioan
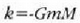 eginez gero,
grabitazio indarra ate- ratzen n da, eta
eginez gero,
grabitazio indarra ate- ratzen n da, eta 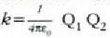 eginez gero, berriz, Coulomben legea lortzen da
eginez gero, berriz, Coulomben legea lortzen da
Materia puntuaren dinamika
Mugimenduaren ekuazioak
Dagikunez, m masa duen zatiki baten mugimenduaren ekuazioa hau da:

non F letraren bidez zatikiaren gainean eta bere a azelerazioan eragiten duen indar osoa edo ondoriozko indarra adierazten baita. Ekuazio horren bektore ekuazioa azalduz gero koordenatu angelu zuzenez osatutako sistema batean ekuazio horrek dituen osagaien arabera, hiru ekuazio eskalar hauek lortuko dira:
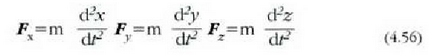
Dinamikaren inguruko arazoak
Dinamikan bi arazo mota izaten da, bata bestearen alderantzizkoa: batetik, materia puntu baten mugimendu legea ezagututa, zerk eragiten duen indarra zehaztea; bestetik, egindako indarra ezagututa, puntuaren mugimendua zehaztea. Lehenengo arazoa deribatuarekin konpontzen da. Bigarren arazoa konpontzen zailagoa da, eta arazo horixe da hain zuzen, puntuaren dinamikan oinarrizko arazoa . Atal honetan bigarren arazo hori aztertuko da.
Demagun m masa duen P puntu mugikor batean F indarrak eragiten duela. Oro har, indar hori bere posizioaren, lastertasunaren eta denboraren funtzioa izango da, hau da:

Puntuaren mugimenduaren ekuazioak dinamikaren oinarrizko ekuazioa bete behar duenez gero:
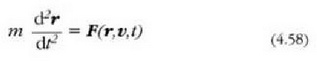
Bigarren mailako ekuazio diferentzial hori integratuz gero, r aterako da t-ren arabera.
Ekuazio horren emaitza orokorrak bi integrazio bektore konstante ditu (edo sei integrazio konstante eskalar:
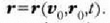 .
Arazo bakoitzean, bi bektore konstante arbitrario horiek mugimenduaren hasierako
baldintzen arabera zehaztu daitezke, hau da, puntu mugikorrak
.
Arazo bakoitzean, bi bektore konstante arbitrario horiek mugimenduaren hasierako
baldintzen arabera zehaztu daitezke, hau da, puntu mugikorrak
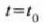 unean dituen posiziotik eta lastertasunetik abiatuta (oro har, t=0 aukeratzen d.a)
unean dituen posiziotik eta lastertasunetik abiatuta (oro har, t=0 aukeratzen d.a)
Berezko ekuazioak
Ibilbidea ezagutzen denean, hau da, s t-ren arabera ezagutzen denean,
m zatikian egiten den F indarra hiru indarretan banatzea komeni izaten da:
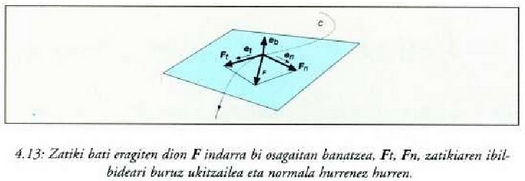
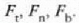 Hiru indar horiek F indarraren proiekzioak diren ukitzailean, normal nagusian eta binormalean, hurrenez hurren:
Hiru indar horiek F indarraren proiekzioak diren ukitzailean, normal nagusian eta binormalean, hurrenez hurren:
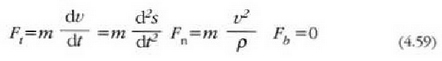
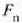 beti positiboa eta
beti positiboa eta 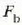 beti baliogabea direnez gero, indarrak alde ahurraren ibilbidearen plano oskulatzailean egon behar du
(4.13 irud).
beti baliogabea direnez gero, indarrak alde ahurraren ibilbidearen plano oskulatzailean egon behar du
(4.13 irud).
F indarra ibilbideari buruz normala eta konstantea bada,
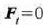 ,
lastertasuna konstantea izango da eta indarra makurduraren erradioaren alderantzizko
arrazoiaren arabera aldatuko da.
,
lastertasuna konstantea izango da eta indarra makurduraren erradioaren alderantzizko
arrazoiaren arabera aldatuko da.
F indarra ibilbideari buruz tangentea eta konstantea bada, orduan:

eta v ez denez gero baliogabea, p infinitua da eta ibilbidea lerro zuzena. Mugimendua plano batean egiten denean, orduan mugimenduaren planoa plano oskulatzailea da, eta tangentea eta normala plano horretan egongo dira.
Adibidea.
Pendulu konikoa
Luzera l duen hari baten muturrean lotuta dagoen m masako zatiki batek r erradioko ibilbide zirkularra egiten du plano horizontal batean zenbakizko v lastertasun konstantean, eta hariak kono baten gainaldea irudikatzen du (pendulu konikoa). Zehaztu hariak bertikalarekin eratzen duen f angelua.
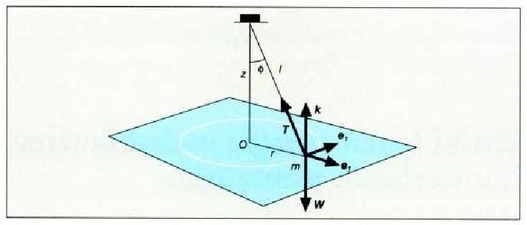
Ebazpena: Zatikiari indar hauek eragiten diote: bere pisuak, W = mg eta hariaren T tentsioak (4.14 irud.). Baldin eta F bada ondoriozko indarra,
F = W + T izango da.
Baina, zatikia plano horizontal batean higitzen denez, z konstantea da eta
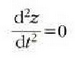
Beraz, z ardatzean zehar formularen emaitza zero da. Orduan,
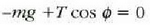
Gainera, v lastertasuna konstantea denez,
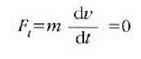
Horrela, beraz, ondoriozko indarrak konstanteki normala izan behar du ibilbideari buruz. Horrenbestez:
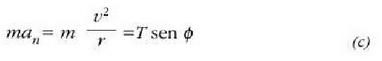
(a) eta (c) ekuazioetatik beste ekuazio hau ateratzen da:

Puntuaren dinamikaren teorema orokorrak
Sarrera
Dinamikaren inguruko arazoak konpontzeko, batzuetan, mugimenduaren ekuazioak integratu ordez, egokiagoa izaten da teorema orokorrak erabiltzea; teorema horiek dinamikaren oinarrizko legearen dedukzioz atereak dira. Teorema horiei esker, bestalde, gertakari jakin batek berezkoak dituen zenbait alderdi aztertu daitezke gertakari osoa ikertu gabe. Horrez gainera, teorema horiek, askotan, arazo askoren konponketa prozesua sinplifikatzen dute.
Integrala indarraren denborarekiko. Bultzadaren teorema
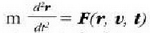 mugimenduaren ekuazio difentzialaren integrazioa egiteko bi sistema erabiltzen dira.
Lehenengoan, indarra denboraz biderkatzen da, eta bigarrenean, indarraren eta puntuaren leku
aldatzearen arteko biderkadura eskalarra egiten da. Ondoren lehenengo sistema aztertuko da.
mugimenduaren ekuazio difentzialaren integrazioa egiteko bi sistema erabiltzen dira.
Lehenengoan, indarra denboraz biderkatzen da, eta bigarrenean, indarraren eta puntuaren leku
aldatzearen arteko biderkadura eskalarra egiten da. Ondoren lehenengo sistema aztertuko da.
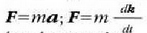 mugimenduaren ekuazioa bider dt egiten bada, hau lortzen da:
mugimenduaren ekuazioa bider dt egiten bada, hau lortzen da:

Ekuazio horren lehenengo osagaia 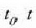 limiteen artean integratuz gero, eta bigarren osagaia
limiteen artean integratuz gero, eta bigarren osagaia 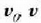 limiteen artean, hau gelditzen da:
limiteen artean, hau gelditzen da:
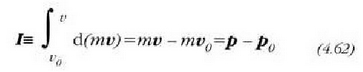
p = mv bektoreari (v lastertasun bektorearen eta m puntuaren masaren arteko biderkadura)
momentu lineala edo mugimendu kurua esaten zaio, eta indarraren denborari buruzko integralari,
 indarraren bultzada.
indarraren bultzada.
Momentu lineala magnitude bektoriala da; momentu horren norabidea eta noranzkoa zatikiaren lastertasunarekin bat datoz. Fisikan garrantzi handiko kontzeptua da momentu lineala; zatiki baten egoera dinamikoaren ezaugarri diren bi osagaiak, masa eta lastertasuna, lotzen ditu.
(4.62) ekuazioak adierazten du indar baten bultzada eta momentu linealaren gorabehera berdinak direla (bultzadaren teorema).
F ez badago denboraren mende, bultzada eta indarraren eta denboraren
arteko biderkadura berdinak dira. Bultzada berdina izandaiteke denbora luzez irauten duen indar
txiki batentzat eta denbora laburreko indar handi batentzat. Beraz, bultzadak indar baten eraginkortasuna neurtzen du.
Bultzadaren eta momentu linealaren banakoak berdinak dira.
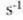 -tan,
eta CGS sisteman dinatan edo g cm
-tan,
eta CGS sisteman dinatan edo g cm 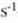 -tan.
-tan.
Mugimenduaren ekuazioa integratzeko metodo hau indarra konstantea denean edo denboraren funtzio ezaguna denean erabiltzen da.
(4.62) ekuazioanp-ren ordez mv jartzen bada, badago ekuazio hori berriz ere integratzea. Hala egiten denean, zatikiaren lastertasuna denboraren arabera lortuko da:

eta v= dr/dt denez gero, beste integrazio baten bidez, zatikiaren posizioa zehatz daiteke, edozein unetan:
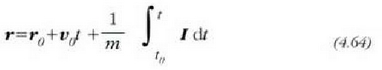
non 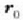 zatikiaren posizio bektorea baita
zatikiaren posizio bektorea baita 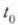 unean, eta r posizio bektorea t unean
unean, eta r posizio bektorea t unean
Adibidea. m = 3 kg masako zatikia 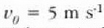 lastertasunean mugitzen da x ardatzaren norabide positiboan. Aurkitu zatiki horri
lastertasunean mugitzen da x ardatzaren norabide positiboan. Aurkitu zatiki horri
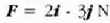 indarrak bi segundoz eraginez gero
zatikiak bi segundoak igaro ondoren izango duen lastertasuna.
indarrak bi segundoz eraginez gero
zatikiak bi segundoak igaro ondoren izango duen lastertasuna.
Ebazpena: Indarraren bultzadari ekuazio hau dagokio:
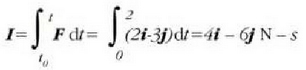
t = 0 denean zatikiaren lastertasuna 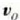 bada eta t = 2 segundotan v bada, orduan:
bada eta t = 2 segundotan v bada, orduan:
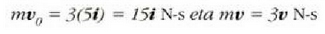
Beraz, (4.62) ekuazioaren arabera
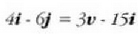 izango da,
izango da,
hau da:
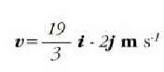
Indarraren integrala leku aldatzeari buruz. Energia zinetikoa
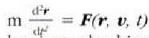 mugimenduaren ekuazioaren integrazioa egiteko aipatu den bigarren metodoa era honetan da:
ekuazio horren bi aldeen eta leku aldatzearen arteko biderkadura eskalarra eginez:
mugimenduaren ekuazioaren integrazioa egiteko aipatu den bigarren metodoa era honetan da:
ekuazio horren bi aldeen eta leku aldatzearen arteko biderkadura eskalarra eginez:
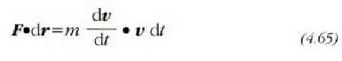
Baina,
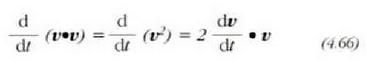
denez gero, hau ateratzen da:
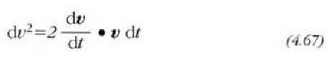
edo bestela, m konstantea dela onartu denez gero:
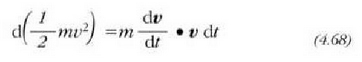
Beraz:
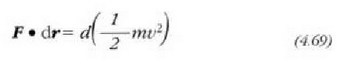
C kurba batean 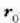 -tik r-ra era
finituan lekuz aldetzeko, indarrak egiten duen lana hau izango da:
-tik r-ra era
finituan lekuz aldetzeko, indarrak egiten duen lana hau izango da:
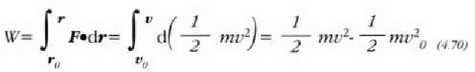
non 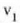 zatikiak amaierako puntuan duen lastertasuna baita eta
zatikiak amaierako puntuan duen lastertasuna baita eta
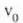 zatikiak hasierako puntuan duen lastertasuna.
zatikiak hasierako puntuan duen lastertasuna.
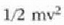 eskalarrari zatikiaren energia zinetikoa esaten zaio; energia zinetikoa T letraz adierazten da.
Azken ekuazio horren arabera, F indarraren forma funtzionala eta zatikiaren ibilbidearen
forma edozein direla ere, indarrak egiten duen lana eta zatikiaren energia zinetikoak izaten
duen aldaketa berdinak dira (energia zinetikoaren aldaketaren teorema).
eskalarrari zatikiaren energia zinetikoa esaten zaio; energia zinetikoa T letraz adierazten da.
Azken ekuazio horren arabera, F indarraren forma funtzionala eta zatikiaren ibilbidearen
forma edozein direla ere, indarrak egiten duen lana eta zatikiaren energia zinetikoak izaten
duen aldaketa berdinak dira (energia zinetikoaren aldaketaren teorema).
F konstantea edo r posizio bektorearen funtzio ezaguna denean erabiltzen da mugimenduaren ekuazioaren integrazio metodo hori. Oro har, energia zinetikoa unetik unera aldatu egiten da, ez da inoiz negatiboa izaten, eta baliogabetu egiten da gorputza geldi dagoenean.
Energia zinetikoa neurtzeko lana neurtzeko erabiltzen diren banako berberak erabiltzen dira.
Zatiki baten energia mekanikoaren kontserbazio printzipioa
Zatiki bati eragiten dion indarra kontserbatzailea denean, (4 .41) eta (4 .70) ekuazioak elkar daitezke . Orduan hau ateratzen da :
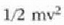
Ekuazio horren lehenengo atala bi energien arteko batura da, energia zinetikoaren eta energia potentzialaren artekoa, alegia. Energia zinetikoa zatikiaren mugimenduari dagokio; potentziala, berriz, posizioari. Ekuazio hori marruskadurarik ez dagoenean aplika daiteke bakarrik; bestalde, energiaren kontserbazioari buruzko legearen kasu berezia da. Gorputz eremu batek funtzio potentziala badu, mugitzen den zatiki baten energia zinetikoaren eta potentzialaren batura konstantea izango da. Energia zinetikoaren eta potentzialaren batuketak energia mekanikoa ematen duenez gero, aurreko esapide horri energia mekanikoaren kontserbazio printzipioa esaten zaio. Eta horregatik esaten da funtzio potentziala duen ndar eremu bat kontserbatzailea dela
Energia potentziala koordenatu bakar baten mende baldin badago, x koordenatuaren mende, esate baterako, orduan azken ekuazio hori beste era honetara idazten da:
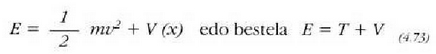
non, E, energia osoa, konstante bat baita.
Mugimendu lerro zuzenerako lastertasunaren balioa v = dx/dt denez gero, ekuazio horrek balio du x lortzeko t-ren arabera, hau da, zatiki baten mugimendu lerro zuzenaren problema ebazteko.
Oharra. 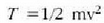 ekuazioa, energia zinetikoa ematen duena batetik, eta W = VO-V ekuazioa,
energia potentziala ematen duena bestetik, konparatzen badira, ikus daiteke lehenengo ekuazioa,
oro har, erabil claitekeela F indarra edozein izanda ere; bigarrena, aldiz, F indarrak
ekuazioa, energia zinetikoa ematen duena batetik, eta W = VO-V ekuazioa,
energia potentziala ematen duena bestetik, konparatzen badira, ikus daiteke lehenengo ekuazioa,
oro har, erabil claitekeela F indarra edozein izanda ere; bigarrena, aldiz, F indarrak
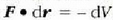 ekuazioa betetzen duenean baizik ezin da baliatu, hau da, indarra V potentzial batetik datorrenean baizik ez.
ekuazioa betetzen duenean baizik ezin da baliatu, hau da, indarra V potentzial batetik datorrenean baizik ez.
Adibidea.
1. Grabitate eremuan higitzen den puntu material askea
Ardatz bertikal gisa goranzko z ardatza hartzen bada, orduan:
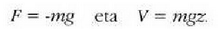
Energia mekanikoaren kontserbazio printzipioaren arabera:
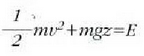
2. Distantziaren proportzionala den indar batek puntu finko batera erakarritako puntu materiala
F(r) = - kr eta 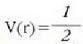 denez, energiaren kontserbazio printzipioaren arabera ondoko adierazpen hau ateratzen da:
denez, energiaren kontserbazio printzipioaren arabera ondoko adierazpen hau ateratzen da:
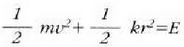
3. Distanziaren koadroari buruz alderantziz proportzionala den indar batek puntu fmko batera erakarritako puntu materiala

denez, energiaren kontserbazio printzipioaren arabera:
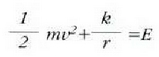
Energiaren kontserbazioa
Sistema bakartu batean, hau da, kanpoko indarren eraginik ez duen sistema batean,
energia zinetikoaren eta energia potentzialaren arteko T + V baturak ez du derrigorrez
konstantea izan behar, izan ere, badira 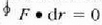 hori hautsi denik, ezezaguna den energia modu berri bat sortu dela baizik.
Energiaren kontserbazio printzipioaren interpretazio horren adibide argia da
neutrinoarena Q desintegrazio teoriaren barruan.
hori hautsi denik, ezezaguna den energia modu berri bat sortu dela baizik.
Energiaren kontserbazio printzipioaren interpretazio horren adibide argia da
neutrinoarena Q desintegrazio teoriaren barruan.
Zatiki baten momentu angeluarra
Zenbaitetan, materia puntu baten mugimendua aztertzean, mv momentu linealaren
bektorea zehaztu beharrean egokiagoa izaten da bektore horren momentu aldaketa zehaztea.
mv bektorearen momentua eta indar baten momentua berdin-berdin kalkulatzen dira.
Demagun m masa duen zatiki bat eta O puntu finko bat daudela (4.15 irud).
Momentu angeluarra O puntuari buruz esaten zaio honela definitutako
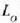 bektoreari:
bektoreari:
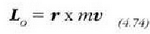
non r eta v-k zatikiaren posizioaren bektorea eta bere lastertasuna O puntuari buruz adierazten duten, hurrenez hurren.
Momentu angeluarra "zatikiaren errotazioaren" neurria da.
m dr/dt zatikiaren momentu lineala denez gero
(mugimendu kopurua), momentu angeluarrari momentuaren momentua ere esaten zaio
(momentu angeluarra esapidea ez da, agian, egokia zatikia lerro zuzenean mugitzen denean
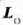 ez baita zero izaten,
lerro hori O puntutik igarotzen ez bada behintzat).
ez baita zero izaten,
lerro hori O puntutik igarotzen ez bada behintzat).
Adibidea. Zatiki baten momentu angeluarra
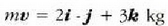
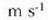 da zatikia (3, 2, -1) puntutik igarotzen denean. Zehaztu zatiki horren momentu angeluarra
koordenatuen sorburuari buruz.
da zatikia (3, 2, -1) puntutik igarotzen denean. Zehaztu zatiki horren momentu angeluarra
koordenatuen sorburuari buruz.
Ebazpena: 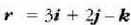 eta
eta
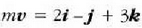 denez:
denez:
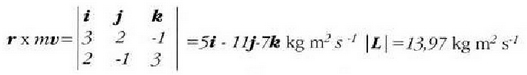
Momentu angeluarraren teorema
Demagun zatiki bati F indar aldakor batek eragiten diola (4.16 irud). Orduan, mugimenduaren ekuazioa hau izango da:

Aurreko adierazpenaren eta r-ren arteko bektore biderkaketa eginez gero, ekuazio hau lortzen da:
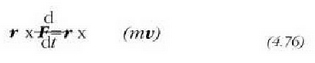
Dena dela, bektore identitatea dela eta,
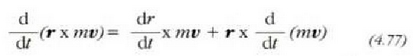
eta kontuan hartuta horretan 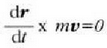 dela, bektore horiekparaleloak baitira, hortaz:
dela, bektore horiekparaleloak baitira, hortaz:
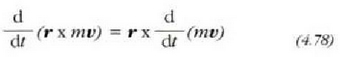
r x F = r x d/dt (mv) ekuazioan azken ekuazio hori ordezkatzen bada, hau lortzen da:
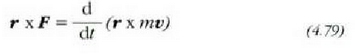
r x F biderkadurak adierazten duenez F indarraren
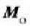 momentua O puntuari buruz, eta r x mv zatikiaren
momentua O puntuari buruz, eta r x mv zatikiaren
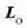 momentu angeluarra
momentu angeluarra
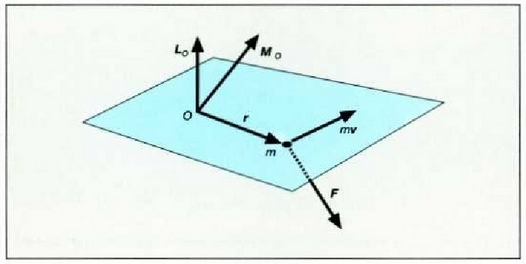
puntu horri herari buruz, aurreko ekuazioa beste era honetan ere idatz daiteke:

hau da, zatiki baten O puntuari buruzko momentu angeluarrarekiko deribatua eta zatiki horretan eragiten duen indarraren O puntu horri buruzko momentua berdinak dira (momentu angeluarraren teorema) . Ondoren ikusiko denez teorema horrek mugimendu ekuazioen lehen mailako integrala ematen du M o baliogabea denean
Momentu angeluarraren kontserbazioa
Zatikia indar zentral baten ekintzaren mende baldin badago, hau da, O puntu finko batetik etengabe igarotzen den norabidea duen indar baten mende baldin badago, orduan puntu hori momentuen zentro bezala hartzen bada, indarraren momentua puntu horri buruz beti zero izango da eta azken ekuazioa beste hau bihurtzen da:

Eta ekuazio hori integratuz gero:
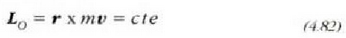
hau da, zatiki bati eragiten dion momentua zero bada, momentu angeluarra kontserbatu egingo da (momentu angeluarraren kontserbazioaren teorema). Zatikiaren ibilbidea O puntutik igarotzen den plano batean dago. Ondoko ekuazioa honen,

non bektore konstantea den c, eta r-ren arteko biderkaketa eskalarra eginez gero, hau lortzen da:
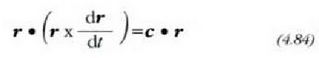
eta ekuazio horren lehenengo atala baliogabea denez (bi faktore berdin dituen bitariko biderkadura), hau lortzen da:

Adierazpen horrek O puntutik igarotzen den bektore ekuazioa adierazten du, eta zuta da c-ri buruz.
Plano hori v-ren eta r-ren lehenengo balioen bidez zehazten da, hau da,
 eta
eta 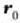 balioen bidez. Beraz, indar zentral baten eraginpean mugitzen den zatiki oro planoa da.
balioen bidez. Beraz, indar zentral baten eraginpean mugitzen den zatiki oro planoa da.
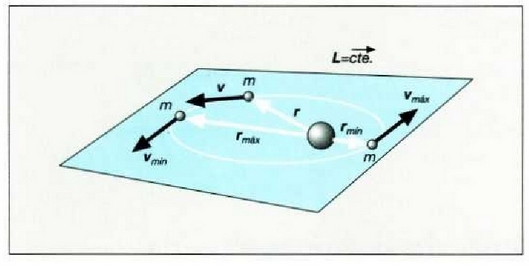
Adibidea. m masa duen Lurraren satelite batek elipse formako ibilbidea egiten du (4.17 irud.).
Satelitetik Lurraren zentrorako gehieneko eta gutxieneko distantziak
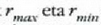 dira, hurrenez hurren.
Zehaztu satelitearen gutxieneko lastertasuna gehieneko lastertasuna
dira, hurrenez hurren.
Zehaztu satelitearen gutxieneko lastertasuna gehieneko lastertasuna
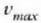 denean.
denean.
Ebazpena. Satelitea indar zentral baten eraginpean mugitzen denez (grabitatea), satelitearen momentu angeluarra konstantea da. Horrenbestez, r txikitzean lastertasuna igo egiten da. Elipse formako orbita batean v lastertasuna r-ren elkarzuta denez, (4.82) ekuazioa erabiliz ondoko adierazpen hau ateratzen da:
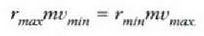
Beraz:
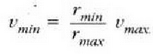
Areen teorema
r x dr/dt bektore biderkaduraren interpretazio geometrikoa oso erraza da. Bedi dt denbora bitarte txikia; bitarte horretan zatikiak dr = vdt bidea egiten du (4.18 irud). Bektore erradioak mugituz dt denboran zehar eratzen duten dA area (alderdi iluna), honen berdina da zenbakiz:
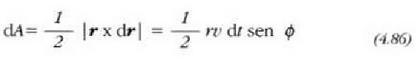
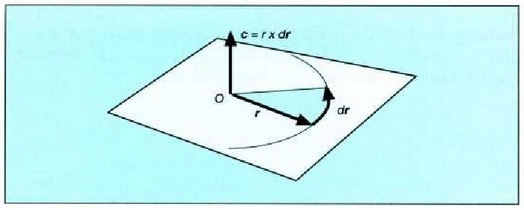
4.18: Indar zentro baten eraginpean dagoen zatiki bat bektore erradioak balio bereko denbora tartean balio bereko areak irudikatzen dituela higitzen da (areen teorema)
non r eta v bektoreek osatzen duten angelua
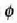 den.
Beraz, arearen lastertasuna dA/dt adierazpenaren bidez definitzen bada,
den.
Beraz, arearen lastertasuna dA/dt adierazpenaren bidez definitzen bada,

ekuazioak adierazten du arearen lastertasuna, edozein indar zentralarentzat, konstantea dela. Azalpen hori Kepler-en bigarren legearekin bat dator; areen teorema esaten zaio
Mugimendu lerro zuzena
Sarrera
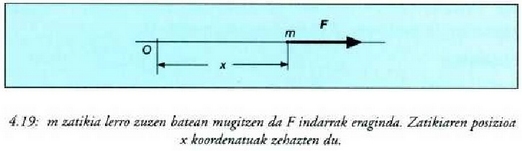
Demagun m masa duen zatikia F indar batek eraginda mugitzen dela lerro zuzen baten gainean (ardatz bezala x hartuko da) (4.19 irud). Zatiki horren mugimenduaren ekuazio bakarra hau izango da:

non, oro har, F indarra x, t eta v lastertasunaren funtzioa den, hau da, F=F (t,x,v).
Bigarren mailako ekuazio diferentzial horri esker, baldin eta ebatz badaiteke, x kalkulatu
ahal izango da t-ren arabera. Ekuazio horren emaitzak,
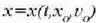 , bi konstante arbitrario edukiko ditu gehienetan.
, bi konstante arbitrario edukiko ditu gehienetan.
Indar konstantea
Demagun F indarra konstantea dela. Orduan, mugimenduaren ekuazioa honela adieraziko da:

Ekuazio horren bi atalak bider dt egin eta integratuz gero, hau lortzen da:
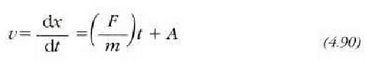
eta berriz integratuz gero:
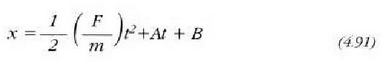
Dena dela, oro har, errazagoa da beste era honetara egitea
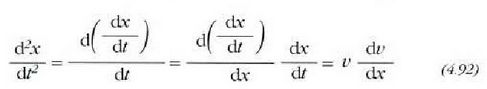
izan ere,  ekuazioan ordezkatuz gero eta denborari buruz integratuz gero, hau ateratzen da:
ekuazioan ordezkatuz gero eta denborari buruz integratuz gero, hau ateratzen da:
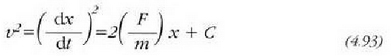
(4.90), (4.91) eta (4.93) ekuazioen bidez, azelerazio konstantean eta lerro zuzenean egindako
mugimenduari buruzko edozer kalkula daiteke. A, B eta C konstanteak hasierako baldintzen arabera zehazten dira.
t = 0 berdintzarako  eta
eta  bada,
orduan aurreko ekuazioek hau ematen dute:
bada,
orduan aurreko ekuazioek hau ematen dute:
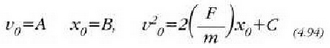
Beraz:
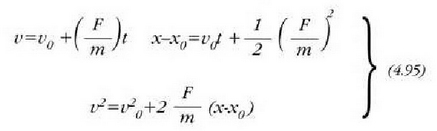
Adibidea. Mugimendu mota honen adibiderik garrantzizkoena Lurraren gainaldetik hurbil grabitatearen eraginpean libre eta airearen erresistentzia eta Lurraren errotazio mugimendu txikia kontuan hartu gabe erortzen den zatikiarena da. Kasu horretan F aldagaiak zatikiaren pisua adierazten du, mg aldagaiaren berdina da, eta mugimendu ekuazio hau dagokio:
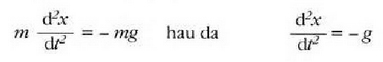
Indarra posizioaren funtzio gisa
Indarra posizioaren funtzio denean, mugimenduaren ekuazioa hau izango da:

non F(x) den x-en funtzioa bakarrik. Ekuazio hori ebazteko bi atalak x-z biderkatu behar dira. Biderkaketa horretatik lortzen da:

Aurreko adierazpenetik deduzitzen da:
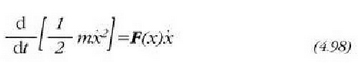
edo bestela,
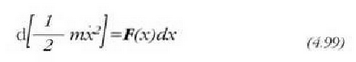
Integratuz gero:
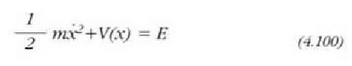
non
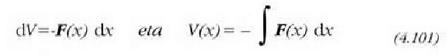
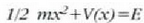 ekuazioak adierazten du mugimenduan zehar, energia zinetikoaren,
ekuazioak adierazten du mugimenduan zehar, energia zinetikoaren,
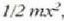 ,
eta potentzialaren, V(x), arteko batuketak konstante irauten cluela. E konstanteak emaitza
osoa adierazten du.
,
eta potentzialaren, V(x), arteko batuketak konstante irauten cluela. E konstanteak emaitza
osoa adierazten du.
x-erako (4.100) ekuazioa ebatziz gero:
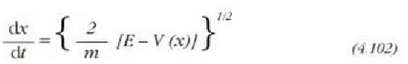
Ekuazio hori integratzeko aldagaiak banandu egiten dira, hau da,ekuazioaren atal batean x aldagaia jarrita eta bestean t aldagaia.Hori eginda hau lortuko da:
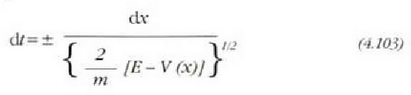
eta integrazioa eginez gero:
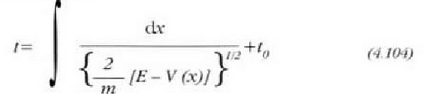
Mugimenduaren ekuazioaren emaitzan diren bi konstante arbitrarioak hauek dira: E energia osoa eta
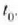 .
Sistemako E energia osoa ezagutzea ez (la mugimenduaren ezaugarri guztiak deduzitzeko nahikoa,
izan ere, horrez gainera
.
Sistemako E energia osoa ezagutzea ez (la mugimenduaren ezaugarri guztiak deduzitzeko nahikoa,
izan ere, horrez gainera 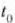 ezagutu behar baita. V(Y) ezagutzen bada, azken ekuazio horren bidez x-en balioa kalkula daiteke
edozein unetan
ezagutu behar baita. V(Y) ezagutzen bada, azken ekuazio horren bidez x-en balioa kalkula daiteke
edozein unetan
Energiaren diagramak
Energiaren kontserbazioaren printzipioaren bidez informazio asko lor daiteke zatiki baten mugimenduaren ingurukoa, baita (4.104) ekuazioaren laguntzarik gabe ere. Hasierako posizioa eta lastertasuna ezagutzen badira h' konstatea kalkula daiteke. Orduan,
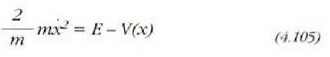
aclierazpenaren bidez, zatikiaren lastertasuna (zeinurik gabea) lor daiteke edozein x posiziorako.
Energia zinetikoa, oinarrian magnitude positiboa denez gero, E energia osoa mugimenduan zehar energia potentziala baino handiagoa izango da beti, hau da, mugimendua V(v) <F_ betetzen den guneetara mugatuko (la. V(x) energia potentzialax leku aldatzearen arabera adierazten bada, hainbat kurba mota lor daitezke. (4.20) irudian erakusten den adibidean, energia potentzialak gutxieneko
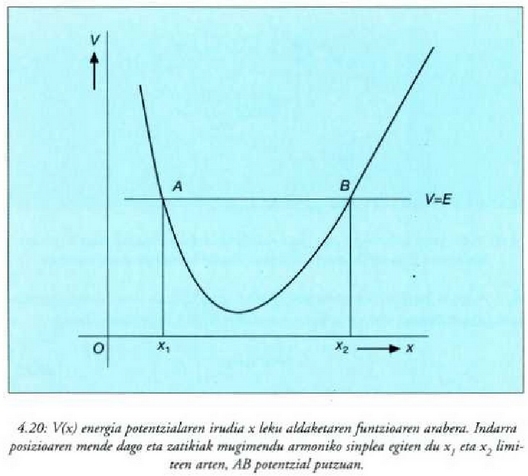
bakarra du. Grafiko horretan E energia osoari dagokion lerro zuzena marrazten bada, berehala
bereiziko dira mugimenduaren mugak. Adibide horretan, mugimendua AB eremuan gerta daiteke hakar
bakarrik. Adibide horretan, V(x) = E betetzen duten puntuek jartzen dituzte mugimenduaren mugak.
Puntu horieigeldiune puntuuk esaten zaie, x lastertasuna zero baita horietan. Esate baterako, zatikia
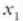 geldialditik abiatzen bada,
eskuinerantz mugituko da, lastertasuna handituz lehenbizi eta txikituz ondoren, harik eta
geldialditik abiatzen bada,
eskuinerantz mugituko da, lastertasuna handituz lehenbizi eta txikituz ondoren, harik eta
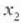 puntura iristen den arte.
Une horretatik aurrera, zatikiak kontrako mugimendua egiten du.
Beraz, zatikiak mugimendu oszilatzailea egiten du AB potentzial puntzuan,
puntura iristen den arte.
Une horretatik aurrera, zatikiak kontrako mugimendua egiten du.
Beraz, zatikiak mugimendu oszilatzailea egiten du AB potentzial puntzuan,
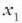 eta
eta 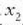 puntuen artean. Baina zatikiak
puntuen artean. Baina zatikiak  -etik
-etik
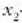 -ra joateko behar duen denbora
-ra joateko behar duen denbora
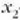 tik x-ra joateko behar duenaren berdina denez gero,
oszilazio denbora (T), hau da, zatikiak
tik x-ra joateko behar duenaren berdina denez gero,
oszilazio denbora (T), hau da, zatikiak 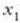 -etik
-etik
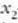 -ra eta
-ra eta
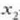 -tik
-tik
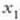 -ra joateko behar duena,
-ra joateko behar duena,
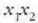 distantzia egiteko behar duen denboraren bikoitza da.
Beraz, (4.103) ekuazioaren arabera,
distantzia egiteko behar duen denboraren bikoitza da.
Beraz, (4.103) ekuazioaren arabera,
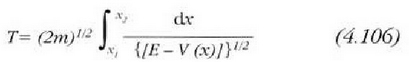
Integrazioaren mugak 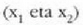 ekuazio erroak dira E balioarentzat. Ekuazio horrek edozein oszilazio mugimenduaren periodoa
zehazten du zatikiaren E energia osoaren arabera.
ekuazio erroak dira E balioarentzat. Ekuazio horrek edozein oszilazio mugimenduaren periodoa
zehazten du zatikiaren E energia osoaren arabera.
Adibidea.
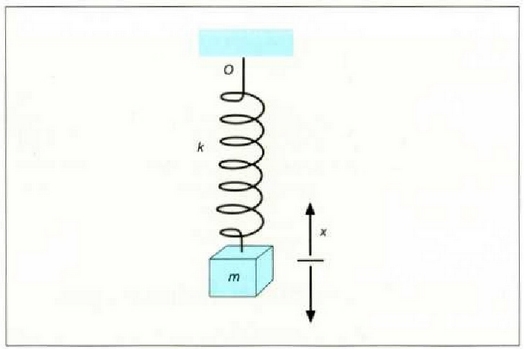
Oszi latzaiile armoniko linealaEman dezagun malguki baten bidez O puntu finko bati lotuta dagoen m masa bat dugula (4.21 irud.). Zatikiaren posizioa. koordenatuak zehazten du eta haren oreka egonkorreko posizioaz = 0 puntuan gertatzen da. Kasu honi m masaren mugimenduaren ekuazio hau dagokio:

non 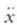 aldagaiak x aldagaiaren denborari buruzko bigarren deribatua adierazten baitu,
F aldagaia indar berreskuratzailea baita, -kx, x- en leku aldaketaren proportzionala,
eta k konstante elastikoa baita (cm - ' indarra). k konstantea malgukiaren «indar» neurri bat da.
aldagaiak x aldagaiaren denborari buruzko bigarren deribatua adierazten baitu,
F aldagaia indar berreskuratzailea baita, -kx, x- en leku aldaketaren proportzionala,
eta k konstante elastikoa baita (cm - ' indarra). k konstantea malgukiaren «indar» neurri bat da.
(a) ekuazioan azaltzen den sistemari oszilatzaile armoniko lineal izena ematen zaio eta mugimendu periodikoaren kasu erraz eta garrantzizkoena da, fisika klasikoko eta fisika kuantikoko problema askoren eredu zehatza, edo gutxi gorabeherakoa, baita.
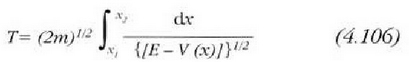
(a) ekuazio diferentziala ebazteko osagai bakoitza bider zatikiaren x egiten (la. Beraz, orduan:
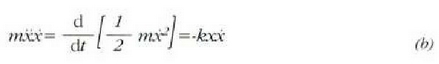
Adierazpen hori integratuz
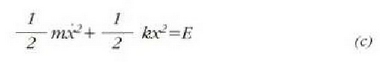
ateratzen da, non E integrazio konstanteak zatikiaren energia osoa adierazten baitu,
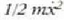 aldagaiak energia zinetikoa eta
aldagaiak energia zinetikoa eta
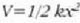 aldagaiak energia potentziala.
Beraz, (c) adierazpena, mugimenduaren ekuazioaren lehen integrala, energiaren ekuazioa
(la [ikus 139. orrialdeko (b) ekuazioa]. E konstantea hasierako baldintzen arabera zehazten da.
Eman dezagun
aldagaiak energia potentziala.
Beraz, (c) adierazpena, mugimenduaren ekuazioaren lehen integrala, energiaren ekuazioa
(la [ikus 139. orrialdeko (b) ekuazioa]. E konstantea hasierako baldintzen arabera zehazten da.
Eman dezagun 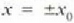 denean
denean 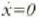 dela, beraz:
dela, beraz:
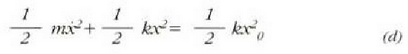
Bigarren mailako (a) ekuazio diferentzialaren ordez lehen mailako ekuazio diferentziala dugu orain. (d) ekuaziotik beste hau ateratzen da:

non  baita.
Aurreko adierazpenaren bidez zatikiaren x lastertasuna kalkula daiteke oreka posizioaren x Teku aldaketaren arabera,
hasierako baldintzak lehen emandako berberak direnean. (e) ekuazioan aldagaiak bakartuz emaitza hau lortzen da:
baita.
Aurreko adierazpenaren bidez zatikiaren x lastertasuna kalkula daiteke oreka posizioaren x Teku aldaketaren arabera,
hasierako baldintzak lehen emandako berberak direnean. (e) ekuazioan aldagaiak bakartuz emaitza hau lortzen da:
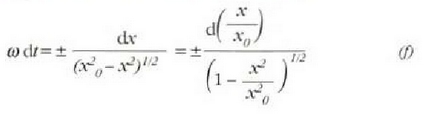
Erroaren zeinu negatiboa hartzen bada, integratzean emaiza hau ateratzen da:
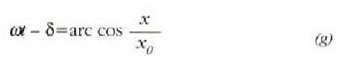
hau da,
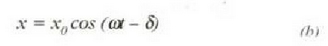
non d integrazio konstante berri bat baita; konstante horren balioa hasierako leku aldatzearen balioa
emango duen hasierako bigarren baldintzatik abiatuta kalkulatzen cia. Eman dezagun t = 0 denean x = 0
(lela, orduan 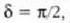 eta t = 0 denean x = x o balitz, orduan
eta t = 0 denean x = x o balitz, orduan 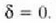
Oharra. Erroaren zeinu positiboa hartu Baliz, emaitza heste hau litzateke:

(h) eta (i) ekuazioek d = 0 denean adierazten dituzten mugimenduen espazio-denborari dagozkion grafikoak 4.22 irudian agertzen elira. I kurba sinu funtzioari dagokio eta 11 kurba, herriz, kosinu funtzioari. Noski, hi kurbek bat egiten clute denboraren ardatzari buruzko leku aldatze erlatibo batean.
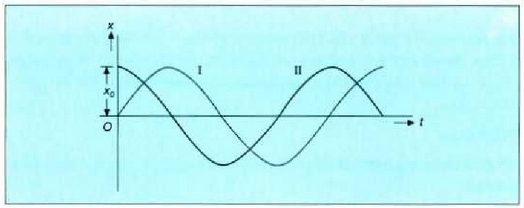
4.22: Denboraren araberako leku aldaketaren grafikak mugimendu armoniko sinplean . I kurba sinu ntzioari dagokio eta II kurba kosinu funtzioari
Energia diagramak. Oszilatzaile armoniko batean, energia potentziala adierazten duen kurba,
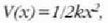 parabola bat cia, eta E energia osoa adierazten duena, berriz, lerro horizontal bat (4.23 irud.).
Zatikiaren mugimendua lerro horizontalak parabola ebakitzen duen puntuen artean dauden x
aldagaiaren balioetara murrizten da, (4. 100) ekuazioaren arabera
parabola bat cia, eta E energia osoa adierazten duena, berriz, lerro horizontal bat (4.23 irud.).
Zatikiaren mugimendua lerro horizontalak parabola ebakitzen duen puntuen artean dauden x
aldagaiaren balioetara murrizten da, (4. 100) ekuazioaren arabera
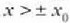 denean energia
zinetikoa negatiboa baitlitzateke eta hori ezinezkoa baita. Goitik beherako lerro bat irudikatzen bada,
energia potentzialaren
denean energia
zinetikoa negatiboa baitlitzateke eta hori ezinezkoa baita. Goitik beherako lerro bat irudikatzen bada,
energia potentzialaren 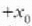 eta
eta 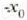 tarteko edozein
x posiziori buruzko V energia potentziala kurbaren ordenatuak emango du eta energia zinetikoa, T = E - V,
parabolaren eta E altura duen zuzen horizontalaren arteko distantziak. Beraz, muturretan energia guztia potentziala da,
eta erdiko posizioan, berriz, zinetikoa.
tarteko edozein
x posiziori buruzko V energia potentziala kurbaren ordenatuak emango du eta energia zinetikoa, T = E - V,
parabolaren eta E altura duen zuzen horizontalaren arteko distantziak. Beraz, muturretan energia guztia potentziala da,
eta erdiko posizioan, berriz, zinetikoa.
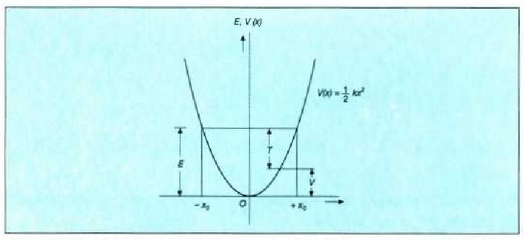
4.23 : E energia osoaren, V energia potentzialaren eta T energia zinetikoaren adierazpena mugimendu armonika sinplea egiten duen zatiki batentzat.
Indarra lastertasunaren funtzio
Demagun F indarra v lastertasunaren funtzioa dela bakarrik, hau da, F=F(v) dela. Orduan:

Adierazpen hori integratuz gero:
nonv=v o berdintza gertatzeko behar den denbora t=to den . Baina, dx=v dt denez gero, m dv/dt = F(v) ekuazioan ordezkatuta, hau lortzen da:
eta integratuz gero:
Hor ikusten da bai x [(4.110) ekuazioa] bai t [(4.108) ekuazioa] v aldagai
auxiliarraren arabera -zatikiaren lastertasuna- adierazten direla.
(4.108) eta (4.110) ekuazioetan v kenduz gero, 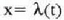 ateratzen da.
ateratzen da.
Adibidea.
Mugimendua gorputzei erresistentzia egiten dien ingurune batean
Gorputz bat airean edo uretan mugitzen denean inguruneak erresistentzia egiten dio gorputzaren mugimenduari.
Lastertasun txikiak direnean 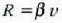 formula erabil daiteke R ingurunearen gutxi gorabeherako erresistentzia adierazteko, non
formula erabil daiteke R ingurunearen gutxi gorabeherako erresistentzia adierazteko, non
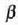 ingurunearen eta
gorputzaren neurriaren eta formaren araberako konstante bat, eta ez masaren araberakoa, baita.
(Lastertasun handietarako,
ingurunearen eta
gorputzaren neurriaren eta formaren araberako konstante bat, eta ez masaren araberakoa, baita.
(Lastertasun handietarako, 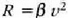 erabiltzen da).
erabiltzen da).
Koordenatuen O sorburua zatikiaren hasierako posizioa bera bada, eta x ardatzaren norabide positiboa gorputzaren mugimenduaren norabidearekin bat badator, mugimenduaren ekuazio diferentziala hau izango da:

Aldagaiak bakartu ondoren gelditzen den ekuaziotik beste adierazpen hau lortzen da:

eta t = 0 denean 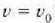 denez, orduan:
denez, orduan:
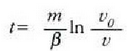
edo bestela
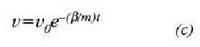
(c) formula integratuz zatikiak ibilitako espazioa eta denbora lotzen dituen ekuazioa lortzen da:
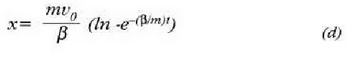
Oharra. Ibilitako espazioa lastertasunaren arabera zehazteko, komenigarria da berriro (a) ekuaziotik abiatzea, ekuazio hori era honetara jarrita:

Adierazpen hori zati v egiten, aldagaiak bakartzen eta x = 0 denean
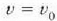 dela
kontuan hartzen bada, emaitza hau ateratzen da:
dela
kontuan hartzen bada, emaitza hau ateratzen da:

v = 0 egiten bada 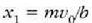 izango da, eta zatikiak mugitzen hasten denetik gelditzen den arte ibilitako espazioa emango du adierazpen
horrek
izango da, eta zatikiak mugitzen hasten denetik gelditzen den arte ibilitako espazioa emango du adierazpen
horrek
Indarra denboraren funtzio gisa 5. Bi zatikiz osaturiko sistema baten dinamika
Demagun indarra denboraren mendekoa dela, hau da, F=F(t) dela. Mugimenduaren ekuazio hau, orduan, erraz ebatz daiteke.

Lehenengo integralak hau ematen du denborari buruz:
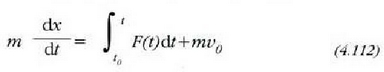
non dx/dt-ren balioa 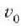 den
den 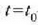 -rako.
-rako.
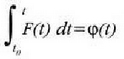 egiten bada, hau lortuko da:
egiten bada, hau lortuko da:
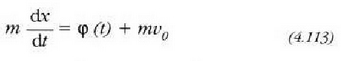
Beste integrazio bat eginez gero, hau idatz daiteke:
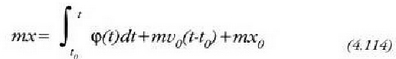
non x-en balioa 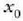 den
den 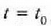 betetzen denerako.
betetzen denerako.
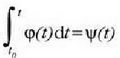 egiten bada, azkenik hau lortuko da:
egiten bada, azkenik hau lortuko da:
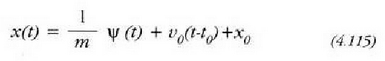
(4.111) ekuazioan adierazitako zatikiaren mugimendua ematen du adierazpen horrek.
Adibidea. m masa duen zatiki bat F indarraren eraginpean mugitzen da lerro zuzen batean zehar eta indarraren magnitudea handitu egiten da denboraren proportzioan, F = kt ekuazioaren arabera. Zehaztu mugimenduaren legea, hasiera unean zatikia geldik dagoela.
Ebazpena. Koordenatuen sorburutzat zatikiaren hasierako posizioa hartzen bada eta x ardatza mugimenduaren norabidetzat, adierazpen hau ateratzen da:
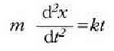
Berdintza horretako bi osagaiak bider dt eginez honela gelditzen da:
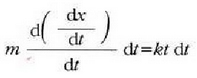
edo
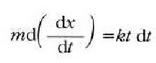
Formula hori integratuz:
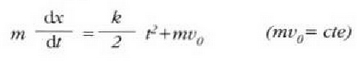
Baina t = 0 denean 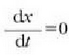 denez,
denez,
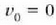 izango da. Beraz:
izango da. Beraz:
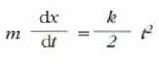
Berriro integratzen da eta ekuazio hau ateratzen da:
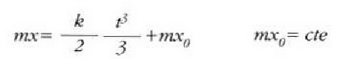
eta t = 0 baliorako x = 0 denez, orduan, azkenik:
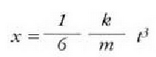
Zatikiak ibilitako espazioa handitu egiten da, beraz, denboraren kuboaren proportzioan
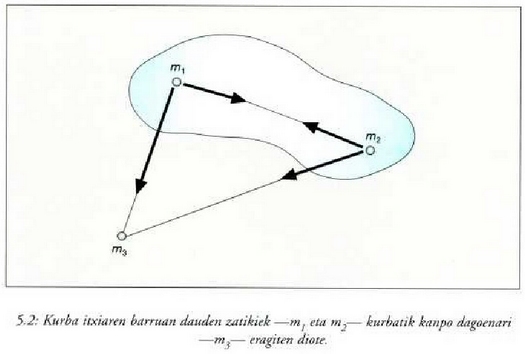
5. Bi zatikiz osaturiko sistema baten dinamika
Sarrera
Indar baten mende dagoen zatiki baten mugimendua aztertu da aurreko atalean, indar hori bere kokalekuaren, lastertasunaren edo denboraren funtzio besterik ez zela. Dinamikaren oinarrizko ekuazioaren eta zatikiaren hasierako baldintzen arabera erabat zehaztuta geratzen zen zatikiaren mugimendua. Atal honetan, ordea, elkarri eragiten dioten bi zatikiz osaturiko sistema bakartu baten mugimendua aztertuko dugu.
Barne eta kanpo indarrak
Bedi sistema bat, bi zatikiz osatua: 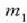 eta
eta 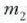 dira zatikien masa, eta
dira zatikien masa, eta
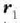 eta
eta
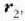 berriz,
hautatu den koordenatu sistema bateko puntuak, hots, zatikien kokalekua (ikus 5.1 irudia). Baldin
berriz,
hautatu den koordenatu sistema bateko puntuak, hots, zatikien kokalekua (ikus 5.1 irudia). Baldin
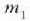 zatikian
zatikian
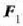 indarrak eragiten badu, eta
indarrak eragiten badu, eta
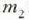 zatikian
zatikian
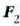 -k, hauek izango dira zatiki horien mugimendu ekuazioak:
-k, hauek izango dira zatiki horien mugimendu ekuazioak:
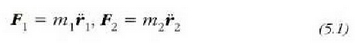
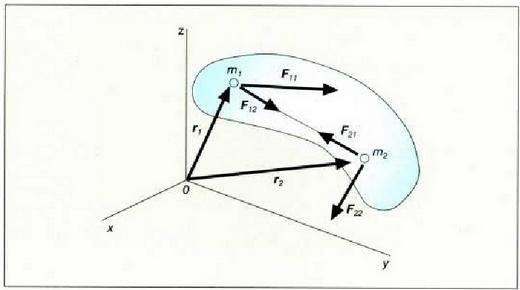
5 .1 : Kanpo eta barne indarrak bi zatikiz osaturiko sistema bati eragiten.
Nolanahi ere, 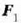 eta
eta 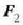 indarrak bi
eratakoak izan daitezke: kanpo indarrak -sistemari kanpotik eragiten diotenak- eta barne indarrak
-sistemaren barruko bi zatikien artekoak-. Eremu elektriko batean dabiltzan bi zatiki kargadun,
batetik, edo Lurra eta Marte, Eguzkiaren grabitate eremuan higituz, bestetik, izan daitezke horren adibide,
indarrak bi
eratakoak izan daitezke: kanpo indarrak -sistemari kanpotik eragiten diotenak- eta barne indarrak
-sistemaren barruko bi zatikien artekoak-. Eremu elektriko batean dabiltzan bi zatiki kargadun,
batetik, edo Lurra eta Marte, Eguzkiaren grabitate eremuan higituz, bestetik, izan daitezke horren adibide,
Honela adieraziko da, heraz, 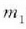 zatikiaren mugimenduaren ekuazioa:
zatikiaren mugimenduaren ekuazioa:

non 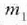 zatikiari eragiten dioten kanpo indarren ondoriozko indarra baita
zatikiari eragiten dioten kanpo indarren ondoriozko indarra baita
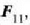 eta
eta
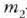 -ren eraginez
-ren eraginez
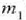 zatikiari eragiten dion barneindarra,
berriz,
zatikiari eragiten dion barneindarra,
berriz, 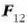 .
Era berean, hau aterako litzateke
.
Era berean, hau aterako litzateke 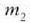 zatikiaren kasuan:
zatikiaren kasuan:

Eta  eta
eta
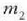 , zatikien mugimendu ekuazioak batuz gero,
hau aterako litzateke:
, zatikien mugimendu ekuazioak batuz gero,
hau aterako litzateke:
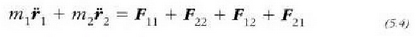
Baina, Newtonen hirugarren legearen arabera, 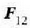 eta
eta 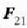 barne indarrak berdinak dira,
eta kontrako noranzkoa dute. Hala heraz,
barne indarrak berdinak dira,
eta kontrako noranzkoa dute. Hala heraz, 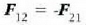 izango da, eta bi zatiki horiek osatzen duten sistemaren mugimenduaren ekuazioa, berriz:
izango da, eta bi zatiki horiek osatzen duten sistemaren mugimenduaren ekuazioa, berriz:
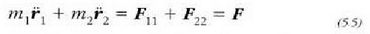
non, 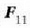 eta
eta
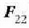 kanpo indarren ondoriozko indarra baita F.
kanpo indarren ondoriozko indarra baita F.
Masa zentroko mugimendua
Aurreko ekuazio hori, baina, bakunagoa bihur daiteke,
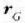 posizio bektorea txertatuz gero; sorburutik bi zatikien masa zentrora doa
posizio bektorea txertatuz gero; sorburutik bi zatikien masa zentrora doa
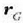 bektorea, eta,
lehenago adierazi den bezala, ekuazio honen bidez definitzen da:
bektorea, eta,
lehenago adierazi den bezala, ekuazio honen bidez definitzen da:
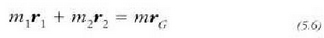
non

ekuazioak sistemaren masa osoa adierazten baitu (ikus 5.3 irudia).
Gero, hartu  adierazpena, eta bi aldiz deribatzen badugu denborari buruz, eta
adierazpena, eta bi aldiz deribatzen badugu denborari buruz, eta
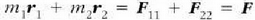 ekuazioan ordezten badugu, hauxe lortzen da:
ekuazioan ordezten badugu, hauxe lortzen da:

alegia: bi zatikiz osaturiko sistema baten masa, batetik, eta sistema osoarena adinako masa masa zentroan bilduta duen eta kanpo indar guztien ondoriozko indar baten eraginpean dagoen zatiki batena, bestetik, berdin-berdinak dira. Baldin konstantea bada F (zatikiak grabitate eremuan daudenean, adibidez, F = mg), azelarazio konstantez higitzen da orduan masa zentroa. Bistan denez, barne indarren masa zentroaren mugimenduan ez du eraginik batere.
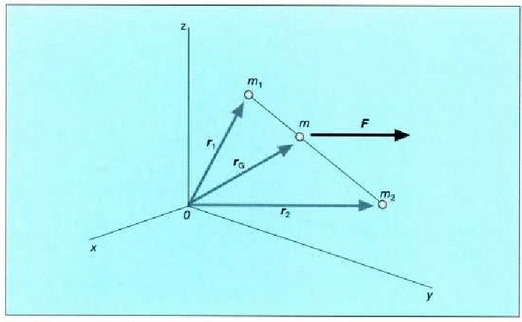
5 .3: Bi zatikiz osaturiko sistema baten masa zentroaren mugimendua
Sistema bakartua. Masa zentroaren kontserbazioaren teorema.
Gorabehera handiko kasu bitxi bat gertatzen da sistemari barne indarrak besterik eragiten ez diotenean, kanpo indarrik ez clenean, alegia. Sistema horri sistema bakartu esaten zaio. Orduan, F = 0 denez:
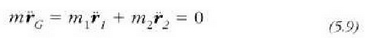
eta
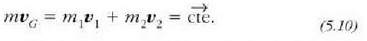
Hau da, sistema bakartu baten masa zentroaren mugimendua lerrozuzena eta uniformea da.
Baina 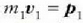 ekuazioak
ekuazioak 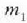 zatikiaren momentu lineala adierazten duenez, eta
zatikiaren momentu lineala adierazten duenez, eta 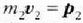 ekuazioak, berriz, m, zatikiaren momentu lineala, beste honetara ere adierazi ahal izango da goraxeagoko ekuazio hori:
ekuazioak, berriz, m, zatikiaren momentu lineala, beste honetara ere adierazi ahal izango da goraxeagoko ekuazio hori:

Masa zentroan dagoen eta masa osoa m duen masa puntual baten mugimendu lineala adierazten du hor
 ekuazioak. Beraz, bi zatikiz osaturiko sistema bakartu baten momentu lineal osoa
mugimenduaren bektore konstante bat da (momentu linealaren
kontserbazioaren teorema).
ekuazioak. Beraz, bi zatikiz osaturiko sistema bakartu baten momentu lineal osoa
mugimenduaren bektore konstante bat da (momentu linealaren
kontserbazioaren teorema).
Masa murriztua.
Bedi bektore bat, 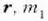 zatikiak
zatikiak
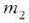 zatikiari buruz hartzen duen leku erlatiboa adierazten duena. Orduan, eta 5.4 irudiaren arabera:
zatikiari buruz hartzen duen leku erlatiboa adierazten duena. Orduan, eta 5.4 irudiaren arabera:

Sistema bakartua dagoela onartzen bada, hau ondorioztatzen da (5.2) eta (5.3) ekuazioetatik, (5.12) kontuan hartuz betiere:
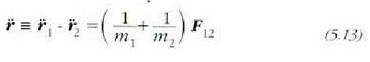
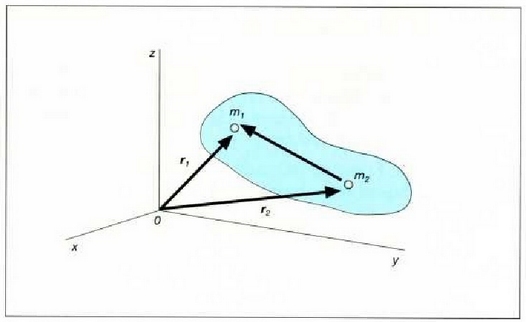
5.4: Elkarri eragiten dioten bi zatikien mugimendu erlatiboa indar zentral baten eraginpean dagoen masa murriztuko zatiki bakar baten mugimenduaren berdina da
Beste magnitude bat txertatuko dugu orain,  magnitudea hain zuzen, masa murriztua deitua, eta ekuazio honen bidez definitua.
magnitudea hain zuzen, masa murriztua deitua, eta ekuazio honen bidez definitua.
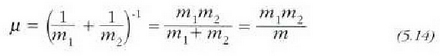
(5.13) ekuazioa beste honetara aldatzen da orduan:

Elkarri eragiten dioten bi zatikien mugimenduaren arazoa, beraz, beste bakunago honetara laburtzen da,
alegia, masa 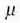 duen eta indar zentral baten eraginpean dagoen zatiki baten mugimendura.
duen eta indar zentral baten eraginpean dagoen zatiki baten mugimendura.
Baldin denboraren arabera ezagutzen baditugu  eta
eta 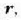 (5.6) eta (5.11) ekuazioak ebatziz lortuko dira
(5.6) eta (5.11) ekuazioak ebatziz lortuko dira 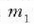 eta
eta  zatikien kokalekuak:
zatikien kokalekuak:
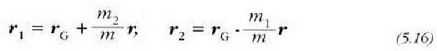
Masa murriztuaren adierazpena moduetako batean idatziz,
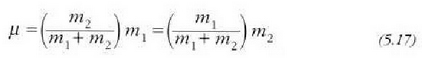
masa murriztua 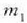 eta
eta
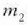 masak baino txikiagoa dela ikusten da
(horregatik esaten zaio masa murriztua).
masak baino txikiagoa dela ikusten da
(horregatik esaten zaio masa murriztua).
Ikus daitekeenez, zatikietako baten masa bestearena baino askoz handiagoa denean -
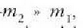 , esate baterako-,
orduan, masa murriztua masa arinena bezalakoa da gutxi gorabehera, hau da:
, esate baterako-,
orduan, masa murriztua masa arinena bezalakoa da gutxi gorabehera, hau da:
 , eta bi masak berdinak direnean,
, eta bi masak berdinak direnean,
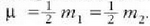
Adibidea. Zehaztu elektroi-protoi sistemaren masa murriztua hidrogeno atomo batean. Nukleoraren masa, gutxi gorabehera, elektroi masa bider 1840 da.
Ebazpena. Izan bitez 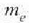 eta
eta
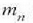 hidrogeno atomoko elektroiaren eta nukleoaren masak.
Hara zer ateratzen den
hidrogeno atomoko elektroiaren eta nukleoaren masak.
Hara zer ateratzen den
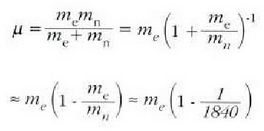
Momentu angeluarra.
(5.8) eta (5.15) adierazpenek
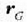 eta r bektoreen arabera ematen dituzte mugimendu ekuazioak.
Zehaztu dezagun orain, bi zatikiz osaturiko sistema baten
eta r bektoreen arabera ematen dituzte mugimendu ekuazioak.
Zehaztu dezagun orain, bi zatikiz osaturiko sistema baten
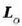 momentu angeluarra
O puntu finko bati buruz
momentu angeluarra
O puntu finko bati buruz 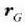 eta r bektoreen arabera.
eta r bektoreen arabera.
Izan bitez 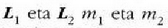 zatikien momentu angeluarrak
O puntu finkoari buruz. Horren arabera,
zatikien momentu angeluarrak
O puntu finkoari buruz. Horren arabera,
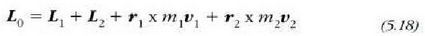
Eta (5.16) ekuazioen arabera, berriz:
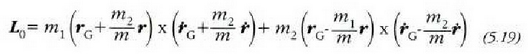
Baina aise ikusten denez, 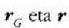 deuseztu egiten dira, eta beste honetara aldatzen da aurreko adierazpen hori:
deuseztu egiten dira, eta beste honetara aldatzen da aurreko adierazpen hori:

Energia zinetikoa
Bi zatikiz osaturiko sistema baten energia zinetikoa zatiki horietako bakoitzaren energia zinetikoen batura da. Hortaz:
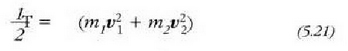
Baina denborari buruz deribatuz gero (5.16) ekuazioak, hau lortuko da:
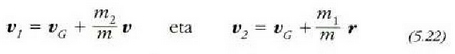
ekuazioan ordeztu, eta eraldatze erraz batzuk egin ondoren, hau atertzen da:
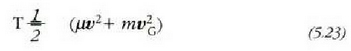
Beraz, bi zatikiz osaturiko sistema baten energia zinetikoa bi terminozko batuketa gisa adieraz daiteke.
Lehenengo terminoa, 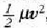 ,
mugimendu erlatiboaren energia zinetikoa da; bigarrena, berriz, (165), bere masa zentroaren
mugimenduaren energia zinetikoa; hau da, masa
,
mugimendu erlatiboaren energia zinetikoa da; bigarrena, berriz, (165), bere masa zentroaren
mugimenduaren energia zinetikoa; hau da, masa 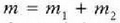 duen eta masa zentroaren lastertasunaz mugitzen den zatiki baten energia zinetikoa.
duen eta masa zentroaren lastertasunaz mugitzen den zatiki baten energia zinetikoa.
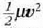 adierazpenari
sistemaren barne energia esaten zaio, eta (165) adierazpenari,
berriz, traslazioko energia zinetikoa.
adierazpenari
sistemaren barne energia esaten zaio, eta (165) adierazpenari,
berriz, traslazioko energia zinetikoa.
Masa zentroko erreferentzia sistema
Lehenago ikusi dugun bezala, sistema bakartu batean, kanpo indarren eraginik batere gabe,
lastertasun konstantean mugitzen da masa zentroa
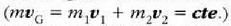 eta zatiki soil baten antzekoa da
sistemaren mugimendua. Hori dela eta, hobe da masa zentroa geldi dagoen erreferentzia sistema batean aztertzea
eta zatiki soil baten antzekoa da
sistemaren mugimendua. Hori dela eta, hobe da masa zentroa geldi dagoen erreferentzia sistema batean aztertzea
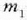 eta
eta
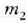 zatikien mugimendua.
Eta sistema horri masa zentroko sistema esaten zaio. Hemendik aurrera izartxo batez (*) adieraziko
dira sistema horri dagozkion magnitudeak.
zatikien mugimendua.
Eta sistema horri masa zentroko sistema esaten zaio. Hemendik aurrera izartxo batez (*) adieraziko
dira sistema horri dagozkion magnitudeak.
Izan bedi, beraz, erreferentzia sistema bat, bere ardatzek -sistema finko baten ardatzen paralelo- beren sorburua masa zentroan
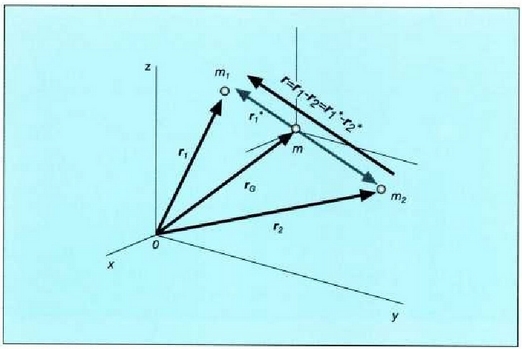
5.5. Bi zatikiren posizio bektoreak masa zentroko erreferentzia sisteman eta erreferentzia sistema finkoan
dutena (ikus 5.5 irudia). Beraz, masa zentroko sistemari buruzko bi zatikien posizio bektoreak
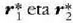 baldin badira:
baldin badira:
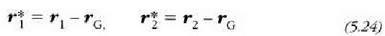
eta

Orobat ere, eta masa zentroaren definizioaren arabera,
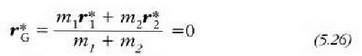
alegia, norabide bera eta kontrako noranzkoa dute
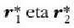 bektoreek.
bektoreek.
Eta (5.26) ekuaziotik ondorioztatzen denez,

Hauxe ateratzen da, beraz, goiko ekuazio hori (5.25) ekuazioan ordeztean:

Horrelaxe lortzen da 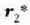 ere:
ere:

Baldin denborari buruz deribatzen badugu (5.27) ekuazioa, eta kontuan hartzen (5.14), (5.28) eta (5.29) ere, hauxe lortzen da:
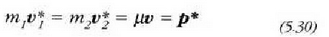
Ekuazio horretan, 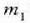 eta
eta 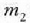 zatikien masa zentroko
erreferentzia sistemako lastertasuna adierazten dute
zatikien masa zentroko
erreferentzia sistemako lastertasuna adierazten dute
 eta
eta
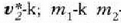 -ri buruz hartzen duen lastertasuna
erlatiboa adierazten du, berriz, v-k; eta
-ri buruz hartzen duen lastertasuna
erlatiboa adierazten du, berriz, v-k; eta 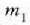 zatikiak masa zentroarekiko duen momentu erlatiboa edo «barne» momentua adierazten du, azkenik,
zatikiak masa zentroarekiko duen momentu erlatiboa edo «barne» momentua adierazten du, azkenik,
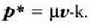
Beraz, masa zentroko erreferentzia sisteman bi zatikien momentu linealak berdinak direla eta elkarren kontrako norabidea dutela adierazten du (5.30) ekuazioak.
5.6 irudian, bi zatikik 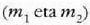 osatzen duten sistema baten masa zentroaren mugimendua adierazi da, laboratorioko erreferentzia sistema batean,
osatzen duten sistema baten masa zentroaren mugimendua adierazi da, laboratorioko erreferentzia sistema batean,
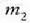 geldi dagoenean, eta,
geldi dagoenean, eta,
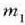 berriz,
berriz,
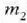 -ra hurbiltzen.
Irudian ikusten denez, masa zentroa zuzen mugitzen da lastertasun konstantean laboratorioko erreferentzia sistemari buruz.
-ra hurbiltzen.
Irudian ikusten denez, masa zentroa zuzen mugitzen da lastertasun konstantean laboratorioko erreferentzia sistemari buruz.
Zatikiaren mugimendua deskribatzeko laboratorioan erabiltzen den koordenatu sistema finkoari esaten zaio laboratorioko erreferentzia sistema.

Orain, berriz, momentu linealaren balioak, momentu angeluarrarenak eta energia zinetikoarenak zehaztu behar ditugu erreferentzia sistema finko batean, edozeinetan, masa zentroko erreferentzia sisteman dagozkien balioen arabera.
Bedi 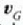 bi zatikien masa zentroaren
lastertasuna erreferentzia sistema finkoan. Orduan, (5.24) ekuazioen arabera, hauek izango dira bi zatikien lastertasunak:
bi zatikien masa zentroaren
lastertasuna erreferentzia sistema finkoan. Orduan, (5.24) ekuazioen arabera, hauek izango dira bi zatikien lastertasunak:
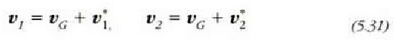
Eta kontuan harturik (5.30), hau ateratzen da:
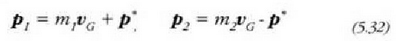
Hona, beraz, momentu angeluar osoa eta energia zinetikoa, (5.20) eta (5.22) ekuazioen arabera, masa zentroko sisteman:
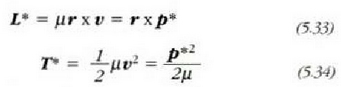
Hala beraz, beste edozein erreferentzia sistema finkorentzat, hauxe beteko da: alegia,
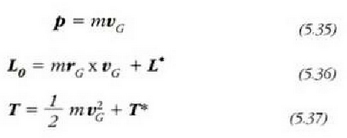
Beraz, edozein erreferentzia sistema finkotan masa zentroko sisteman dagozkion balioetatik abiaturik
 eta T lortzeko, aski da
balio horiei masa zentroan dagoen m masako zatiki baten ekarria
eranstea.
eta T lortzeko, aski da
balio horiei masa zentroan dagoen m masako zatiki baten ekarria
eranstea.
Edozein zatiki kopururako orokortu daitezke aurreko emaitza horiek
Bi zatikiren talka elastikoa
Sarrera
Dituen erabilerak direla eta, oso gauza jakingarria da bi zatikien arteko talka, fisika atomikoarentzat eta nuklearrarentzat batez ere . Esperimentu bidez aztertzen denean, erreferentzia sistema finkoa erabiltzen da laboratorioan ; sistema horretan, zatikietako bat geldi dagoen bitartean, harengana hurbiltzen da bestea, lastertasun jakin batean . Hala ere, talkak errazago aztertzen dira masa zentroa erreferentziatzat duen koordenatu sistema batean
Talka elastikoa
Bi zatikik talka egiten dutenean eta energia zinetikoa galtzen ez denean, hau da, sistemaren energia zinetiko osoa talka baino lehen eta talkaren ondoren berdina denean, talka elastikoa dela esaten da.
Eman dezagun masa zentroko erreferentzia sisteman 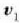 eta
eta 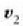 direla, hurrenez hurren, zatikien lastertasunak. Momentu lineala kontserbatzeko teoremaren arabera,
talka baino lehen eta talkaren ondoren, berdinak eta kontrako norabidea izan behar dute zatiki bien momentuak.
direla, hurrenez hurren, zatikien lastertasunak. Momentu lineala kontserbatzeko teoremaren arabera,
talka baino lehen eta talkaren ondoren, berdinak eta kontrako norabidea izan behar dute zatiki bien momentuak.
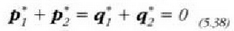
non zatikien talka ondorengo momentua adierazten baitute
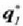 eta
eta 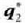 aldagaiek.
Zatikietako bakoitza, beraz, angelu bera
aldagaiek.
Zatikietako bakoitza, beraz, angelu bera 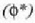 desbideratzen da (ikus 5.7 irudia). Hala ere, talka elastikoa denez, eta (5.34) ekuazioaren arabera:
desbideratzen da (ikus 5.7 irudia). Hala ere, talka elastikoa denez, eta (5.34) ekuazioaren arabera:

eta

Hau da, talka elastiko batean, masa zentroko erreferentzia sisteman dauden bi zatikien momentuen moduluak ez dira aldatzen.
Laboratoriko erreferentzia sisteman,
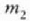 zatikia geldi dago hasieran.
Orduan, talka baino lehen
zatikia geldi dago hasieran.
Orduan, talka baino lehen 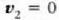 denez,
zatiki horren momentua zero izango da: alegia,
denez,
zatiki horren momentua zero izango da: alegia,
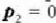 .
Bedi
.
Bedi 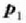 zatiki jotzailearen momentua,
eta
zatiki jotzailearen momentua,
eta 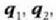 berriz,
berriz,
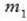 eta
eta
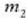 -ren momentuak talka egin ondoren.
-ren momentuak talka egin ondoren.
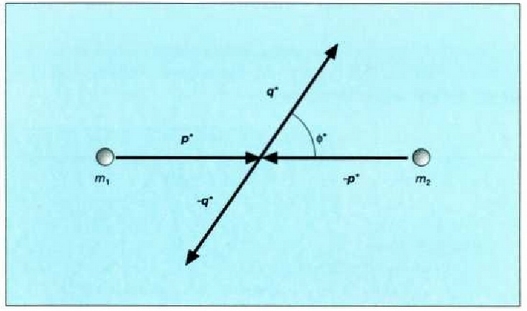
5.7 Talka elastikoa masa zentroko erreferentzia sisteman.
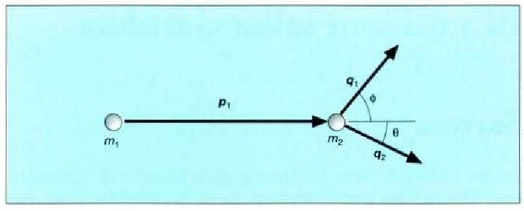
5 .8: Talka elastikoa loabaratoriako erreferentzia sisteman
Baldin  eta
eta
 desbideratze angelua
eta atzeranzko angelua badira hurrenez hurren (rkus 5.8 irudia), eta
desbideratze angelua
eta atzeranzko angelua badira hurrenez hurren (rkus 5.8 irudia), eta
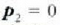 dela kontuan izanik,
hauxe ateratzen ola (5.32) ekuazioan ordeztuz gero:
dela kontuan izanik,
hauxe ateratzen ola (5.32) ekuazioan ordeztuz gero:

eta
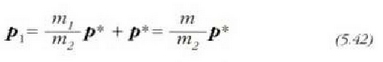
Eta (5.32) ekuazioaren arabera, eta (5.41) kontuan hartuz, hauek izango dira bi zatikien momentuak talkaren ondoren:
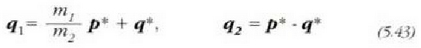
Hurrengo irudiko bektore diagraman (ikzts 5.9 irudia) (5.42) eta (5.43) bektore ekuazioak
eta laboraturiko sisteman momentua kontserbatzeko ekuazioa
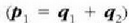 irudikatu dira.
Momentuen, energien eta angeluen arteko erlazio oro zehaztu daiteke diagrama
hori oinarri harturik.
irudikatu dira.
Momentuen, energien eta angeluen arteko erlazio oro zehaztu daiteke diagrama
hori oinarri harturik.
Ekuazio hauen bidez ematen dira atzeranzko angelua
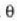 eta momentuaren modulua, masa zentroko sisteman neurtuak:
eta momentuaren modulua, masa zentroko sisteman neurtuak:

eta

Hau da, beraz, laboratoriko erreferentzia sisteman geldi dagoen zatikiari erantsitako energia zinetikoa:
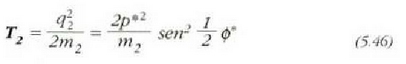
eta sistema horretan, zatiki jotzailearen energia zinetikoa da, hain justu, energia zinetiko osoa; (5.42) ekuazioaren arabera, balio hau du zatikiaren energia zinetikoak:
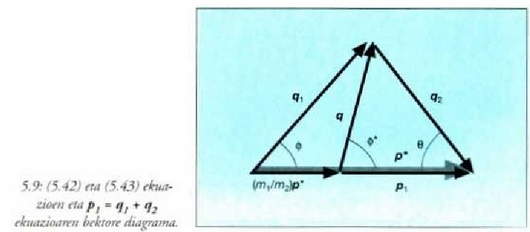
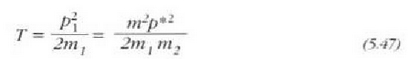
Garrantzi handikoa ola halaber desbideratze angeluen artean dagoen erlazioa bai laboraturiko erreferentzia sisteman bai masa zentroko erreferentzia sisteman. Eta 5.9 irudiaren arabera:

Erlazio hori ez olago bi zatikien momentuen mende, masen arteko erlazioaren mende baizik.
Adibidea
Nukleo zatikien talka laboratorio sisteman
Eman dezagun 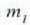 masako alfa zatiki bat ON ibilbide zuzen batean zehar mugitzen dela eta geldi dagoen
masako alfa zatiki bat ON ibilbide zuzen batean zehar mugitzen dela eta geldi dagoen
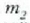 masako atomo nukleo batekin
talka egiten duela (5.10 irudia). Talkaren ondoren, alfa zatikia NA norabidean mugitzen da eta nukleoa NB norabidean,
masako atomo nukleo batekin
talka egiten duela (5.10 irudia). Talkaren ondoren, alfa zatikia NA norabidean mugitzen da eta nukleoa NB norabidean,
 eta
eta 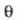 direla desbideratze eta atzerako angeluak.
direla desbideratze eta atzerako angeluak.
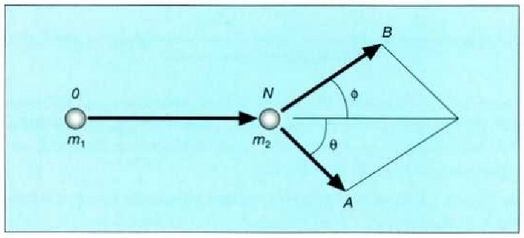
5.10:: Bi nukleo zatikiren talka elastikoa .
Izan bitez 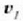 alfa zatikiaren hasierako lastertasuna eta
alfa zatikiaren hasierako lastertasuna eta
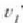 talkaren ondorengo lastertasuna,
eta nukleoarenak herriz, 0 eta
talkaren ondorengo lastertasuna,
eta nukleoarenak herriz, 0 eta 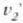 , hurrenez hurren.
, hurrenez hurren.
Nola ez dagoen sistemaren gaineko inolako indarrik momentu linealak lehenean jarraitzen du. Beraz:
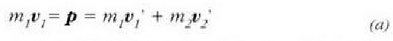
Bektore ekuazio hau ondoko bi ekuazio eskalarren balio berekoada:
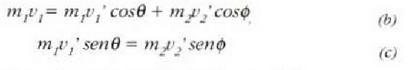
Lehen ekuazioak mugimencluaren hasierako norabidean momentuak lehenean jarraitzen duela
adierazten du eta bigarrenak, hasierako mugimenduaren norabide zutean momentuak lehenean jarraitzen duela.
Bi ekuazio horiek ez dira nahikoa, ordea, 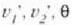 eta
eta  ezezagunak ebazteko.
Energiaren kontserbazio legeak beste ekuazio bat eskaintzen digu:
ezezagunak ebazteko.
Energiaren kontserbazio legeak beste ekuazio bat eskaintzen digu:
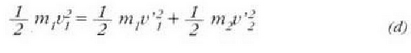
(b) eta (c) ekuazioek bide ematen digute,  ezabatuta,
ezabatuta, 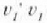 ren funtzioan adierazteko:
ren funtzioan adierazteko:

Era berean, 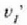 ezabatzen badugu ekuazio berberetatik,
ezabatzen badugu ekuazio berberetatik, 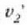 lortuko dugu
lortuko dugu 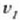 ren funtzioan:
ren funtzioan:
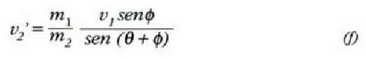
Azkenik, (e) eta (f), (d)n ordeztuta, lastertasunak ezabatuko ditugu eta lortzen den ekuazioan
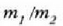 masa erlazioa soilik
masa erlazioa soilik
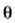 eta
eta
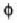 angeluen funtzioan egongo da:
angeluen funtzioan egongo da:
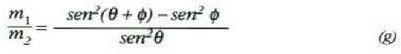
Ondokoa idazten badugu:
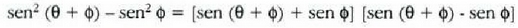
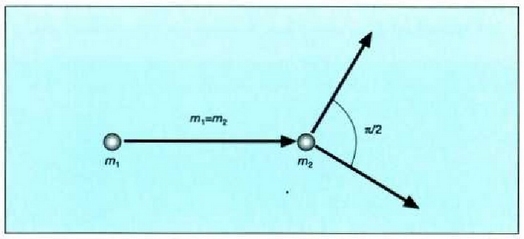
eta kontuan hartzen badugu
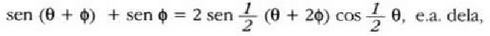
azkenean zera lortzen da:
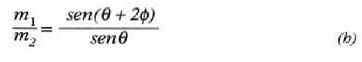
Emaitza honek, 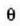 eta ç
eta ç
 neurtu besterik gabe,
alfa zatikiaren eta atomo nukleoaren masen arteko erlazioa zehaztea ahalbidetzen digu.
neurtu besterik gabe,
alfa zatikiaren eta atomo nukleoaren masen arteko erlazioa zehaztea ahalbidetzen digu.
Alfa zatikiak talkaz jotzen duen nukleoa helio nukleoa baldin bada, orduan
 eta
eta
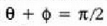 (5.11 irudia).
Eta
(5.11 irudia).
Eta 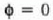 baldin bada, orduan,
(h)ren arabera,
baldin bada, orduan,
(h)ren arabera, 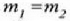 izan behar du,
eta beraz, alfa zatikia geldi geratzen da,
izan behar du,
eta beraz, alfa zatikia geldi geratzen da, 
6. Uhin mugimendua
Sarrera
Uhin mugimendua fisikaren hainbat alorretan agertzen den gertaera da.
Horren adibide dira, besteak beste, uraren gainaldeko uhinak, soinu uhinak eta
uhin elektromagnetikoak. Uraren uhinek eta soinu uhinek ingurune material jakinak,
ura eta airea hain zuzen, behar dituzte espazioan hedatzeko; uhin elektromagnetikoek
(irratia, infragorriak, argi ikusgarria, X izpiak eta
 izpiak)
eta mugitzen ari den atomo zatiki bati dagozkion uhin materialek, aldiz, ez dute inolako
ingurune materialik behar hedatzeko.
izpiak)
eta mugitzen ari den atomo zatiki bati dagozkion uhin materialek, aldiz, ez dute inolako
ingurune materialik behar hedatzeko.
Uhin bat oreka egoera batean sortzen den perturbazio bat da, denborarekin espazioan zehar hedatzen dena.
Uhin motak
Bi uhin mota nagusi daude: luzetarakoak eta zeharretarakoak. Luzetarako uhinetan, uhinak hedatzen diren noranzko berean oszilatzen dute inguruneko zatikiek, eta zeharretarakoetan, aldiz, uhinen hedapen noranzkoari buruz perpedikularrean oszilatzen dute.
6.1 irudian luzetarako uhin bat ikusten da, hodi baten barneko gasa hodiaren mutur batean dagoen pistoi bat txandaka mugitzen denean sorturiko uhina, hain zuzen ere. Kasu honetan gas molekulak hodiaren ardatzaren norabide berean mugitzen dira. Luzetarako uhinak eratzen dira, halaber, metalezko ziri baten mutur bat jotzen denean (6.2 irudia). Kasu honetan uhin elastiko bat sortzen da eta ziri guztian zehar hedatzen da uhin hori. Ziriaren materialaren zatikiak ez dira gune batetik bestera aldatzen; uhin elastikoa da zirian zehar hedatzen dena. Irudian gune batzuk besteak baino ilunago ikusten dira; gune horiek batez besteko dentsitatea baino dentsitate handiagoa dutela esan nahi du horrek.
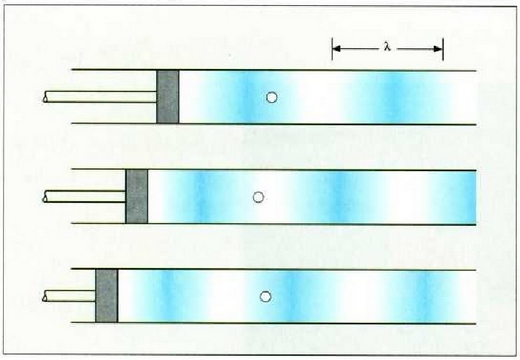
61 : Gas bat duen hodi batean hodiaren muturretako batean dagoen pistoia mugitzean eratzen duen luzetarako uhina.
Zeharretarako uhinei dagokienez, zeharretarako uhinak eratzen dira, esaterako, soka tenkatu batean, sokaren mutur bati zeharretarako mugimendu batek eragiten dionean (6.3 irudia).

62: Metalezko ziri batean ziroaren mutur bat jotzean eratzen den luzetarako uhina
63: Soka tenkatu batean sokaren mutur bati zeharretarako mugimendu batek eragiten dionean eratzen den zeharretarako uhina.
Sokaren zatikiak sokaren norabideari buruz perpendikularrean mugitzen dira beti, eta ez dute sokaren norabidearen paraleloan inolako mugimendurik egiten
Uhin baten deskribapen matematikoa dimentsio batean
Gauza jakina denez, puntu baten mugimendua deskribatzeko ezinbestekoa da puntu hori une bakoitzean non dagoen jakitea. Adibidez, deskribatu nahi den puntua x ardatzean zehar mugitzen bada, x = f(t) ekuazioa ebatzi behar da; ekuazio horretan, puntuaren mugimendu motaren araberakoa izango da f funtzioa. Deskribatu nahi den mugimendua uhin mugimendua denean ordea, puntu guztiek une bakoitzean duten kokaera ezagutu behar da, hau da, u uhin perturbazioax abzisaren eta t denboraren funtzioa da, hots, u = f (x, t). Ekuazio honetan x eta t aldagaiak aldagai askeak dira, hau da, edozein balio har dezakete; x eta t aldagaien balio bakoitzari u uhin perturbazioaren balio jakin bat dagokio. Aldiz, x = f(t) ekuazioan, x eta t aldagaiak ez dira aldagai askeak.
Uhin perturbazio bati t = 0 unean dagokion kurba 6.4 irudian agertzen dena bada, orduan:
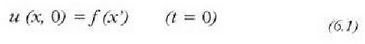
Perturbazioa v lastertasun konstatean mugitzen bada eta mugimendu horretan forma aldatzen ez bazaio, t denbora tartean vt distantzia beteko du. Baina, 6.4 irudiak x' = x - vt betetzen dela erakusten duenez, eta kontuan harturik u(x, 0) = f (x) eta u (x, t) = f(x) direla, perturbazioaren forma ez baita aldatzen, ondoko adierazpena betetzen da:

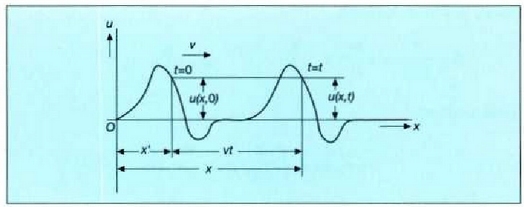
6.4 : Uhin beraren bi une adierazteko funtzio bakar bat erabil daiteke, elkarretatik vt distantziara dauden bi koordenatu sistema harturik funtzio bakar horrentzat
Adierazpen horri uhinaren ekuazioa esaten zaio.
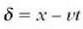 magnitudea uhinaren fasea da. Fasea konstantea bada, u(x, t) ere konstantea izango da.
Eta.x - vt konstantea denez,
magnitudea uhinaren fasea da. Fasea konstantea bada, u(x, t) ere konstantea izango da.
Eta.x - vt konstantea denez, 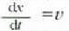 berdintza dt beteko da. Beraz, perturbazioaren hedapen lastertasuna fasearen lastertasunaren berdina da.
berdintza dt beteko da. Beraz, perturbazioaren hedapen lastertasuna fasearen lastertasunaren berdina da.
Baldin eta (6.2) ekuazioan ondoko aldaketa egiten bada:
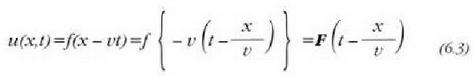
orduan, uhinaren deskribapen matematikoaren beste adierazpen bat aterako da, aurrekoaren baliokidea:

Ikusten denez, t = 0 unean f(x') funtzioak adierazten cluen uhinari f (x - vt) funtzioa dagokio t = t unean,
hasierako funtzioan x' aldagaiaren ordez (x - vt) jartzen bada.
x ardatzaren norabide positiboan, forma aldatu gabe, hedatzen den uhin bati dagokio f(x - vt)
funtzioa, soilik x eta t aldagaiak (x - vt) konbinazioan agertzen diren kasuetan, adibidez,
A cos(wt - bx), 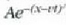 , etab.
, etab.
Adibidea. t = 0 uneko uhin perturbazioari 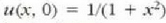 adierazpena dagokio. Baldin eta perturbazio hori v lastertasunean leku aldatzen bada,
aurkitu t uneari dagokion uhinaren forma. Adierazi uhinaren forma t = 1 eta t = 2 uneetan.
adierazpena dagokio. Baldin eta perturbazio hori v lastertasunean leku aldatzen bada,
aurkitu t uneari dagokion uhinaren forma. Adierazi uhinaren forma t = 1 eta t = 2 uneetan.
Ebazpena. Uhinaren forma lortzeko u(x, 0) adierazpenean x aldagaiaren ordez x - vt jartzen da, hau da,
 . 6.5 irudian uhinari t = 1 eta t, = 2
uneetan dagokion forma agertzen da.
. 6.5 irudian uhinari t = 1 eta t, = 2
uneetan dagokion forma agertzen da.
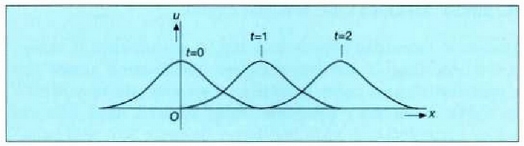
(6.2) ekuazioan vt aldagaiak luzera jakin bat adierazten clu. Beraz, perturbazio bat neurtzen ari diren
bi behatzailek -t = 0 uneko perturbazioa neurtzen badu batek, eta t unekoa besteak- emaitza bera
lor dezaten, behatzaile baten eta bestearen arteko distantziak vt izan behar du.
(6.4) adierazpenean,.x/v zatikiak denbora ematen du aditzera.
Beraz, x puntuko perturbazioa neurtzen ari den behatzaile batek jatorrian
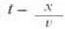 unean zegoen perturbazio bera aterako du emaitza.
unean zegoen perturbazio bera aterako du emaitza.
(6.2) adierazpena baliagarria cla x ardatzaren noranzko positiboan heclatzen den uhin batentzat. Zeinu negatiboak x koordenatuaren balioaren aurretik claudenak dira. Uhina x ardatzaren noranzkonegatiboan hedatzen denean, beraz, alderantzizko zeinua jarri behar zaio x - vt konbinazioari. Kasu horretan, uhinaren ekuazioa hau izango da:
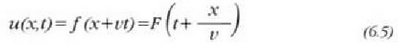
Uhin armonikoak
Kasu aipagarria da u(x, t) perturbazioa ondoren adierazten den tankerako sinu funtzioa edo funtzio armonikoa denean gertatzen dena:
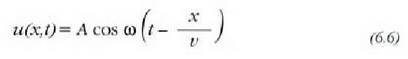
non uhinaren anplitudea baita A, hau da, perturbazioaren balio handiena, eta w maiztasun zirkularra. Kosinuaren argumentua, w(t - x/v), fasea da 6.6 irudian u uhinaren grafikoa azaltzen da x ardatzari buruz eta t une jakin baterako. Bi C puntuei, u funtzioak gehieneko balioa duen puntuei, gailur esaten zaie, eta V puntuak, u funtzioak gutxieneko balioa duen puntuak, hondoak dira. Balio horiek A anplitudearekin bat datoz.
Baldin eta x ardatzean zehar fase bereko eta ondoz ondoko bi puntu,
 eta
eta
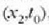 hartzen badira
hartzen badira
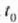 une jakin batean, orduan:
une jakin batean, orduan:
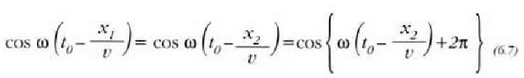
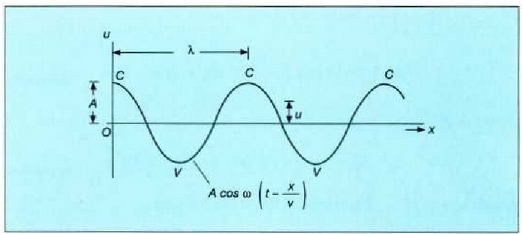
izan ere,  betetzen da, eta horrenbestez:
betetzen da, eta horrenbestez:

eta
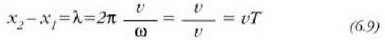
non  uhin luzera baita,
fase bereko bi puntu bereizten dituen gutxieneko distantzia alegia, T periodoa eta v maiztasuna.
Gauza jakina denez
uhin luzera baita,
fase bereko bi puntu bereizten dituen gutxieneko distantzia alegia, T periodoa eta v maiztasuna.
Gauza jakina denez 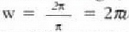 betetzen dela,
ondoko adierazpen hau dagttkiox positiboetarantz v lastertasun konstantean mugitzen den uhin armoniko bati:
betetzen dela,
ondoko adierazpen hau dagttkiox positiboetarantz v lastertasun konstantean mugitzen den uhin armoniko bati:
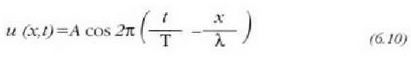
edo, bestela,
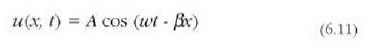
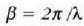 kopuruak
kopuruak
 distantzian dauden uhin
luzeren kopurua ematen du aditzera, hau da uhin kopurua. (6.11) ekuazioa erabiliko da aurrerantzean.
distantzian dauden uhin
luzeren kopurua ematen du aditzera, hau da uhin kopurua. (6.11) ekuazioa erabiliko da aurrerantzean.
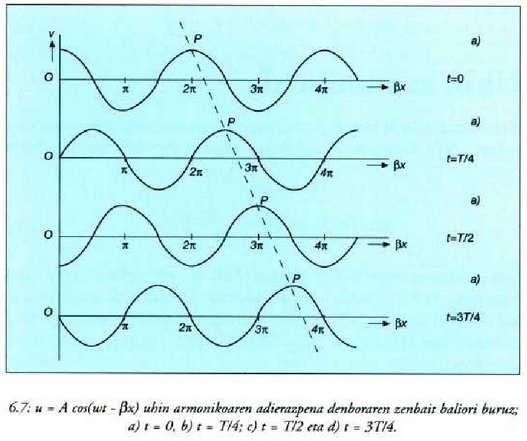
6.7 irudian u(x, t) funtzioa irudikatu da x ardatzaren arabera eta tdenboraren zenbait baliori buruz. t = ta = 0 betetzen denean,emaitza hau da:

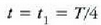 denean,
denean,  da eta
da eta
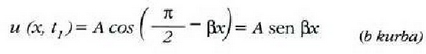
 denean,
denean,
 da eta
da eta

Azkenik,  denean,
denean,
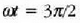 da eta
da eta
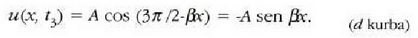
Uhin horietako baten gailurrari, P puntu gisa adierazi den puntuari adibidez, erreparatzen bazaio, ikusten da denboraren balioa zenbat eta handiagoa izan, orduan eta ezkerrerago dagoela gailurra, P kasu honetan.
Adibidea.
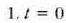 denboran ondoko forma hau du uhin armoniko sinpleak:
denboran ondoko forma hau du uhin armoniko sinpleak:
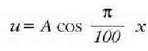
Adierazpen horretan u eta x aldagaien balioa zentimetrotan adierazten dira eta t aldagaiarena segundotan.
Uhinaren lastertasuna 50 cm 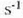 da eta x
ardatzaren norabide positiboan hedatzen da. Zehaztu t = 3 segundori dagokion uhinaren ekuazioa.
da eta x
ardatzaren norabide positiboan hedatzen da. Zehaztu t = 3 segundori dagokion uhinaren ekuazioa.
Ebazpena.
Uhin armonikoen ekuazioa (6.11) ekuazioak ematen duenez, orduan:
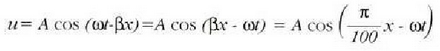
Baina, kontuan harturik
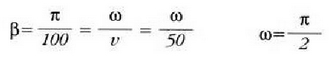
dela, orduan:

t = 3 segundorentzat,
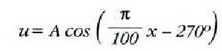
2. Zehaztu 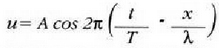 ekuazioak definitzen
duen uhinari edozein unetan dagokion forma.
ekuazioak definitzen
duen uhinari edozein unetan dagokion forma.
Ebazpena. t = T egiten bada, adibidez, orduan, une horretan
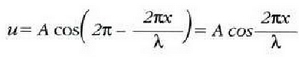 izango da.
izango da.
6.8 irudian ekuazio horri dagokion grafikoa agertzen da eta harturiko unean ondoz ondoko zatikien leku aldatzea adierazten du.
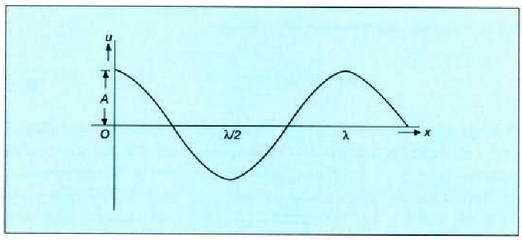
Obarra. Zatiki bati edozein unetan dagokion oszilazioa kalkulatzeko x = 0 egiten da, adibidez.
Horrela 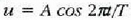 ateratzen da.
Beraz, uhin bat irudikatzeko bi kurba lau behar dira.
ateratzen da.
Beraz, uhin bat irudikatzeko bi kurba lau behar dira.