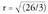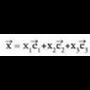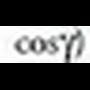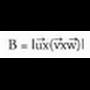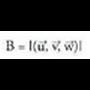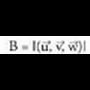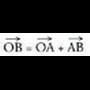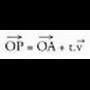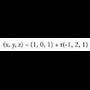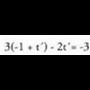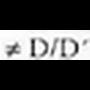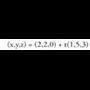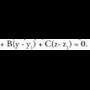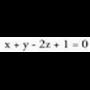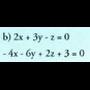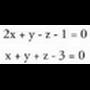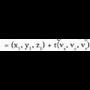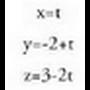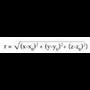Matematika»Geometria
Geometria analitikoa espazioan
I. Sarrera.
Planoko problemak ebazteko erabilitako geometria analitikoko metodoak espazioan ere erabil daitezke, aldaketa handi-handirik egin gabe. Espazioko puntu bakoitza, erreferentzi sistema bat definitu ondoren, bektore batez eta haren koordenatuak diren hiru zenbakiren bidez definitzen da. Gauza geometrikoen baldintzak edo tasunak, beren koordenatuek parte hartzen duten ekuazio bihurtzen dira. Ekuazio horiek, aljebra erabiliz ebazten edo eraldatzen dira ikertu nahi diren gauza geometrikoez ondorioak ateratzeko.Dimentsioetako bat gehitzean (planoan bi ziren, espazioan hiru dira) problemak eta ariketak konplexuago bihurtzen dira. Aztertu eta ikasi beharreko gauza berriak azaltzen dira, hala nola, planoak, esferak, eta abar. Zuzenak berak gutxienez ere bi ekuazio behar ditu espazioan ongi zehaztuta egoteko, bektore batek dituen norabide perpendikularren kopurua infinitua da eta ekuazio guzti-guztiak konplexuagoak dira hiru ezezagun dituztelako. Baina problemak berak eta ebazteko moduak, planoan ikusitakoen antzekoak dira.Espazioan, bektore arteko bi eragiketa berri sartzen dira. Eragiketa horiek lagungarri dira azalerak edo bolumenak kalkulatzeko edota perpendikularrak aurkitzeko. Lehenengo atalean eragiketa berri horiek eta hiru dimentsiotako bektore espazioak ikusiko ditugu eta ondoren zuzenak, planoak, angeluak, distantziak eta gisakoak ikasi eta esferaren berri ikasiz amaituko dugu.
II Hiru dimentsiotako bektore espazioa.
Bektore biderkadura. Biderkadura mistoa.
Hiru dimentsiotan, oinarri batek, , hiru bektore ditu eta edozein x bektore, oinarri horretako bektoreen konbinazio lineal gisa jar daiteke :
, hiru bektore ditu eta edozein x bektore, oinarri horretako bektoreen konbinazio lineal gisa jar daiteke : Hiru dimentsiotako bektore espazio batean, edozein bektore espaziotan bezala, bektoreak beren modulu, norabide eta noranzkoaz ezaugarrituta daude eta bektore batura eta biderkadura eskalarra definituta daude. Oinarri bat emanik, bektore bakoitzari, oinarri horretan dituen bere hiru koordenatuak dagozkio. Oinarria ezagututa, x bektorea definituta gelditzen da bere hiru koordenatuak emanda
Hiru dimentsiotako bektore espazio batean, edozein bektore espaziotan bezala, bektoreak beren modulu, norabide eta noranzkoaz ezaugarrituta daude eta bektore batura eta biderkadura eskalarra definituta daude. Oinarri bat emanik, bektore bakoitzari, oinarri horretan dituen bere hiru koordenatuak dagozkio. Oinarria ezagututa, x bektorea definituta gelditzen da bere hiru koordenatuak emanda . Errenkada matrize moduan ere adieraz daiteke
. Errenkada matrize moduan ere adieraz daiteke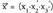 bereizketako kakotxik gabe edota baita zutabe matrize moduan ere
bereizketako kakotxik gabe edota baita zutabe matrize moduan ere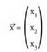 Angeluak edo distantziak bezalako tasun metrikoak aztertzeko,
biderkadura eskalarra definitzen da. Orokorki, edozein oinarritan
emandako bi bektoreren biderkadura eskalarrak balio hau du :
Angeluak edo distantziak bezalako tasun metrikoak aztertzeko,
biderkadura eskalarra definitzen da. Orokorki, edozein oinarritan
emandako bi bektoreren biderkadura eskalarrak balio hau du :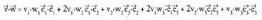 Baina, planoan bezalaxe, oinarria modulua bat duten eta elkarri buruz zutak diren bektoreez eratuta baldin badago, bi bektoreren biderkadura eskalarra,
Baina, planoan bezalaxe, oinarria modulua bat duten eta elkarri buruz zutak diren bektoreez eratuta baldin badago, bi bektoreren biderkadura eskalarra,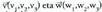 bektoreena alegia, era honetara gelditzen da laburtuta :
bektoreena alegia, era honetara gelditzen da laburtuta :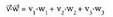 Baldintza horiek betetzen dituzten oinarriei ortonormal edo cartesiar deritze, eta
Baldintza horiek betetzen dituzten oinarriei ortonormal edo cartesiar deritze, eta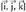 idazkeraz adierazten da. Oinarri ortonormal bateko bektoreek, hau betetzen dute :
idazkeraz adierazten da. Oinarri ortonormal bateko bektoreek, hau betetzen dute :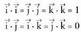 Oinarri ortonormal batean emanda dauden bektoreak,
Oinarri ortonormal batean emanda dauden bektoreak,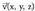 moduan adieraziko ditugu :
moduan adieraziko ditugu :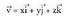 Oinarri horretan v-k modulu hau du :
Oinarri horretan v-k modulu hau du :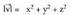 Bi bektore baldin baditugu,
Bi bektore baldin baditugu,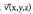 eta
eta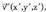 , bien artean eratzen duten angeluaren kosinuak balio hau du :
, bien artean eratzen duten angeluaren kosinuak balio hau du :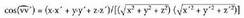 Espazioan, planoan bezala, orientazio edo biraketa noranzko bat badago positibotzat hartua. Orientazio positiboa erloju orratzen aurkako noranzkoan egindako biraketari dagokio, planoan bezalaxe. Espazioan zailago gerta daiteke, beharbada, biraketa baten noranzkoa edo orientazioa zein den ikustea, izan ere, hori egin daitekeen planoak infinitu dira. Horregatik, erreferentzia moduan, koordenatu ardatz bat beste baterantz daraman biraketa erabili ohi da. Ardatzekin, biraketa positiboa honako hau da :
Espazioan, planoan bezala, orientazio edo biraketa noranzko bat badago positibotzat hartua. Orientazio positiboa erloju orratzen aurkako noranzkoan egindako biraketari dagokio, planoan bezalaxe. Espazioan zailago gerta daiteke, beharbada, biraketa baten noranzkoa edo orientazioa zein den ikustea, izan ere, hori egin daitekeen planoak infinitu dira. Horregatik, erreferentzia moduan, koordenatu ardatz bat beste baterantz daraman biraketa erabili ohi da. Ardatzekin, biraketa positiboa honako hau da : bektoreari dagokion ardatza marrazteko ohitura dago, OX ardatza alegia, marrazkia ikusten ari denarenganantz norabidetua,
bektoreari dagokion ardatza marrazteko ohitura dago, OX ardatza alegia, marrazkia ikusten ari denarenganantz norabidetua, bektorea eta OY ardatza, horizontala eta
bektorea eta OY ardatza, horizontala eta bektorea gorantz norabidetua. Geometria analitikoan, Cavalieri perspekiban egiten dira marrazkiak, baina ez dira planoan eginak bezain erabilgarriak.
bektorea gorantz norabidetua. Geometria analitikoan, Cavalieri perspekiban egiten dira marrazkiak, baina ez dira planoan eginak bezain erabilgarriak.
Banako bektorea. Norabide kosinuak.
Norabide jakin batean modulua bat duen bektore bat edukitzea interesatzen bada, bektore horren osagaiak bere moduluaren balioaz zatitu behar dira. Osagai bakoitza, bektorearen luzeraz zatituta, bektore horrek osagai horri dagokion ardatzarekiko eratzen duen angeluaren kosinua ematen du. Horregatik, hiru ardatzetako banako bektorearen osagaiei norabide kosinu deritze.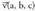 bektorea emanda, bere norabide berbera duen
bektorea emanda, bere norabide berbera duen banako bektorea ezagutu nahi badugu, v bektorea bere moduluaz zatituko dugu :
banako bektorea ezagutu nahi badugu, v bektorea bere moduluaz zatituko dugu : bektoreak OX, OY eta OZ ardatzekin eratzen dituzten angeluak
bektoreak OX, OY eta OZ ardatzekin eratzen dituzten angeluak eta
eta badira, hau betetzen da :
badira, hau betetzen da : Beraz, norabide jakin bateko banako bektorea,
Beraz, norabide jakin bateko banako bektorea,
Biderkadura bektoriala.
Biderkadura bektoriala, bi bektoreren, artean egindako biderkaketa eragiketa da, baina biderkadura horrek beste bektore bat, u, du emaitza, era honetan definitzen dela :- u bektore horren modulua, biderkatzaile diren bi bektoreen
biderkadura bider horiek eratzen duten angeluaren sinua da.
artean egindako biderkaketa eragiketa da, baina biderkadura horrek beste bektore bat, u, du emaitza, era honetan definitzen dela :- u bektore horren modulua, biderkatzaile diren bi bektoreen
biderkadura bider horiek eratzen duten angeluaren sinua da. - u bektorearen norabidea,
- u bektorearen norabidea,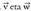 bektoreek zehazten duten planoari buruz zuta da, hots,
bektoreek zehazten duten planoari buruz zuta da, hots, .
. bektorearen noranzkoa,
bektorearen noranzkoa,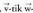 -rantzako biraketan noranzko positiboak ematen duena da.
-rantzako biraketan noranzko positiboak ematen duena da.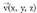 eta
eta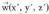 bektoreak, oinarri ortonormal batean daude emanak eta froga daiteke biderkadura bektorialak honako osagai hauek dituela :
bektoreak, oinarri ortonormal batean daude emanak eta froga daiteke biderkadura bektorialak honako osagai hauek dituela : laburbilduta era honetan idatz daiteke :
laburbilduta era honetan idatz daiteke : Hori zenbakizko determinante moduan garatu behar dela ulertzen
da, nahiz eta lehenengo errenkadan bektoreak eduki.Tasunak:1. Biderkadura bektoriala lineala da bi bektoreetan, hau da :
Hori zenbakizko determinante moduan garatu behar dela ulertzen
da, nahiz eta lehenengo errenkadan bektoreak eduki.Tasunak:1. Biderkadura bektoriala lineala da bi bektoreetan, hau da :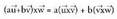 eta
eta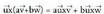 non
non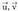 eta
eta bektoreak diren eta a eta b zenbaki errealak.Tasun hau definizioaren ondorio baino ez da, eta erraz onartzen
da biderkadura bektoriala determinante moduan definitzen bada.2. Bektore batek bere buruarekin ematen duen biderkadura bektoriala, zero da,
bektoreak diren eta a eta b zenbaki errealak.Tasun hau definizioaren ondorio baino ez da, eta erraz onartzen
da biderkadura bektoriala determinante moduan definitzen bada.2. Bektore batek bere buruarekin ematen duen biderkadura bektoriala, zero da,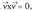 , izan ere, bi bektoreek 0°-ko angelua eratzen baitute elkarrekin, eta sin 0°= 0 da.3.
, izan ere, bi bektoreek 0°-ko angelua eratzen baitute elkarrekin, eta sin 0°= 0 da.3. da, izan ere, biderkatzen diren bi bektoreen ordena aldatzean, orientazio positiboa, emaitza bektorea aurkako noranzkoan bideratuz lortzen baita.4. Oinarriko bektoreek berdintza hauek betetzen dituzte :
da, izan ere, biderkatzen diren bi bektoreen ordena aldatzean, orientazio positiboa, emaitza bektorea aurkako noranzkoan bideratuz lortzen baita.4. Oinarriko bektoreek berdintza hauek betetzen dituzte :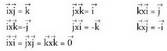 definiziotik erraz ondorioztatzen den bezala.Interpretazio edo ulermen geometrikoa.Aldeak
definiziotik erraz ondorioztatzen den bezala.Interpretazio edo ulermen geometrikoa.Aldeak eta
eta dituen paralelogramo bat baldin badugu, paralelogramoaren A azalerak biderkadura bektorialaren moduluaren balioa du :
dituen paralelogramo bat baldin badugu, paralelogramoaren A azalerak biderkadura bektorialaren moduluaren balioa du : Izan ere, biderkadura bektorialaren modulua honako hau baita :
Izan ere, biderkadura bektorialaren modulua honako hau baita :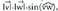 , eta paralelogramoaren azalera oina bider altura da.
, eta paralelogramoaren azalera oina bider altura da.
Oin moduan bektorea hartzen bada, haren luzera
bektorea hartzen bada, haren luzera da, eta alde horrekiko altura
da, eta alde horrekiko altura da.
da. Bi bektori buruz zuta den bektore baten kalkulua.Definizioz, biderkadura bektorialeko emaitza bektoreak bi bektore biderkatzaileri buruz zuta izan behar du. Beraz, ezagunak diren bi bektoreei buruz zuta den bektorea lortzeko modu soil bat, beren biderkadura bektoriala kalkulatzea da.
Bi bektori buruz zuta den bektore baten kalkulua.Definizioz, biderkadura bektorialeko emaitza bektoreak bi bektore biderkatzaileri buruz zuta izan behar du. Beraz, ezagunak diren bi bektoreei buruz zuta den bektorea lortzeko modu soil bat, beren biderkadura bektoriala kalkulatzea da. eta
eta emanik,
emanik, bektorea, biei buruz zuta da.Adibidea:1. Kalkula ezazu
bektorea, biei buruz zuta da.Adibidea:1. Kalkula ezazu eta
eta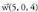 bektoreen arteko biderkadura bektoriala eta egiaztatu
bektoreen arteko biderkadura bektoriala eta egiaztatu emaitza,
emaitza, eta
eta biderkatzaileei buruz zuta dela.
biderkatzaileei buruz zuta dela.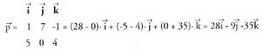 Elkartzutak direla frogatzeko, biderkadura eskalarra zero dela
egiaztatu behar da.
Elkartzutak direla frogatzeko, biderkadura eskalarra zero dela
egiaztatu behar da.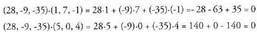 Beraz elkartzutak dira.2. Kalkulatu
Beraz elkartzutak dira.2. Kalkulatu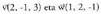 bektoreei buruz zuta den bektore bat.
bektoreei buruz zuta den bektore bat.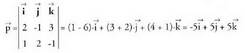 Beraz, bektore perpendikular bat (-5, 5, 5) da. Bektore perpendikular bat kalkulatu ondoren, ahal bada bederen, sinplifikatzea komeni da. Kasu honetan
Beraz, bektore perpendikular bat (-5, 5, 5) da. Bektore perpendikular bat kalkulatu ondoren, ahal bada bederen, sinplifikatzea komeni da. Kasu honetan hartuko litzateke, izan ere koefiziente soilagoak baititu.3. Triangelu baten aldeak bat datoz
hartuko litzateke, izan ere koefiziente soilagoak baititu.3. Triangelu baten aldeak bat datoz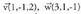 eta
eta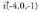 bektoreekin. Kalkulatu triangeluaren azalera.Triangeluaren azalera,
bektoreekin. Kalkulatu triangeluaren azalera.Triangeluaren azalera,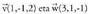 aldeak dituen para- lelogramo baten azaleraren erdia da.
aldeak dituen para- lelogramo baten azaleraren erdia da.
Biderkadura mistoa.
 eta
eta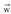 bektoreak emanda, lehenengo bektorearen eta beste
bien biderkadura bektorialaren arteko biderkadura eskalarrak ematen
duen zenbakiari
bektoreak emanda, lehenengo bektorearen eta beste
bien biderkadura bektorialaren arteko biderkadura eskalarrak ematen
duen zenbakiari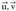 eta
eta biderkadura misto deritzo eta
biderkadura misto deritzo eta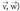 idazten da:
idazten da: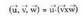 Oinarri ortonormal batean egindako biderkadura mistoa hiru
bektoreak beren ordenan errenkadatzat dituen determinantea kalkulatuz
aurkitzen da :
Oinarri ortonormal batean egindako biderkadura mistoa hiru
bektoreak beren ordenan errenkadatzat dituen determinantea kalkulatuz
aurkitzen da :
Ulertzeko modu geometrikoa :
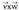 biderkadura bektorialaren modulua
biderkadura bektorialaren modulua eta
eta aldetzat dituen paralelogramoaren azalera da.
aldetzat dituen paralelogramoaren azalera da.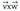 norabidea,
norabidea,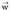 eta
eta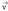 bektoreek zehazten duten planoari buruz zuta da. Bektore horren eta
bektoreek zehazten duten planoari buruz zuta da. Bektore horren eta bektorearen arteko biderkadura eskalarra eginez gero,
bektorearen arteko biderkadura eskalarra eginez gero, eta
eta aldetzat dituen paralelogramoaren azalera bider
aldetzat dituen paralelogramoaren azalera bider bektoreak
bektoreak eta
eta bektoreen norabide perpendikularrean duen proiekzioa da emaitza. Hori hain zuzen ere, zeinua alde batera utzita, oinaren azalera bider
bektoreen norabide perpendikularrean duen proiekzioa da emaitza. Hori hain zuzen ere, zeinua alde batera utzita, oinaren azalera bider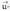 -ren mutur horretan marratutako altura da, hots,
-ren mutur horretan marratutako altura da, hots, eta
eta alde desberdinak dituen paralelepipedoaren bolumena.Zeinua bektoreek duten ordenaren baitakoa denez eta bolumenak beti ere kopuru positiboa izan behar duenez, biderkadura mistoaren balio absolutua hartzen da
alde desberdinak dituen paralelepipedoaren bolumena.Zeinua bektoreek duten ordenaren baitakoa denez eta bolumenak beti ere kopuru positiboa izan behar duenez, biderkadura mistoaren balio absolutua hartzen da eta
eta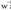 aldetzat dituen paralelepipedoaren bolumena kalkulatzean :
aldetzat dituen paralelepipedoaren bolumena kalkulatzean : Tasunak edo ezaugarriak.1. Biderkadura mistoa lineala da hiru bektoreetan, hau da :
Tasunak edo ezaugarriak.1. Biderkadura mistoa lineala da hiru bektoreetan, hau da :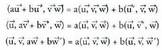 2. Bi bektore aldatzen badira, biderkadura mistoa zeinuz aldatzen
da :
2. Bi bektore aldatzen badira, biderkadura mistoa zeinuz aldatzen
da : Adibideak :1. Kalkula ezazu
Adibideak :1. Kalkula ezazu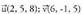 eta
eta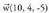 bektoreen biderkadura mistoa.
bektoreen biderkadura mistoa.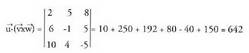 2. Kalkula ezazu paralelepipedo baten bolumena, erpin berean elkartzen diren hiru aldeak edo ertzak ondorengo bektoreak direla jakinda :
2. Kalkula ezazu paralelepipedo baten bolumena, erpin berean elkartzen diren hiru aldeak edo ertzak ondorengo bektoreak direla jakinda :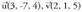 eta
eta
Determinantearen kalkulua
Espazioko geometrian badira hainbat egoera determinante batek kalkuluak
sinplifikatzen dituenak :- Hiru bektore linealki askeak edo independenteak diren ala ez jakin
nahi baldin bada, matrize bat eratzen da bektore horien koordenatuak
errenkadetan edota zutabeetan dituela. Matrize horren determinantea zero
ez bada, hiru bektoreak linealki askeak dira. Zero den determinanteak,
errenkada edota zutabea osatzen duten bektoreen arteko konbinazio lineala
eta ez hutsala dagoela adierazten du eta horrek ematen du zero bektorea.- Biderkadura bektoriala edota biderkadura mistoa, zuzen-zuzenean
kalkulatzen da determinante baten bidez. Biderkadura horiekin kalkula
daitezkeen azalerak eta bolumenak determinante bat kalkulatzera laburbiltzen
dira.- Zuzen edota planoen arteko ebakidurak ebatzi beharra den ekuazio
sistemetan ere oso erabilgarriak dira determinanteak.Hori guztia dela eta, komenigarria da hemen aljebran emandako matrize
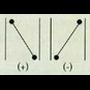
karratuaren determinantea kalkulatzeko arauak laburki bederen gogoraraztea:Matrizea 2x2-koa bada, hau izango dugu :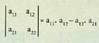 2x2 matrizearen determinantea, diagonal nagusiko gaien biderkadura
ken diagonal bigarreneko gaien biderkadura da.3x3 erako matrizearentzat berriz :
2x2 matrizearen determinantea, diagonal nagusiko gaien biderkadura
ken diagonal bigarreneko gaien biderkadura da.3x3 erako matrizearentzat berriz :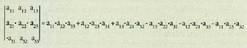 Eta irudi honen bitartez gogoratzen da :
Eta irudi honen bitartez gogoratzen da : Zeinu positiboko biderkadurak diagonal nagusiari buruz paraleloak
dira eta negatiboak diagonal bigarrenari buruz paraleloak.Adibideak:
Zeinu positiboko biderkadurak diagonal nagusiari buruz paraleloak
dira eta negatiboak diagonal bigarrenari buruz paraleloak.Adibideak:
- Ariketak
1. Kalkula itzazu ondoko biderkadura bektorial hauek :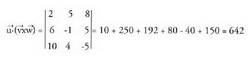 2. Kalkula ezazu paralelepipedo baten bolumena, erpin berean elkartzen diren hiru aldeak edo ertzak ondorengo bektoreak direla jakinda :
2. Kalkula ezazu paralelepipedo baten bolumena, erpin berean elkartzen diren hiru aldeak edo ertzak ondorengo bektoreak direla jakinda : eta
eta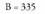 2. Kalkula itzazu ondoko biderkadura misto hauek :
2. Kalkula itzazu ondoko biderkadura misto hauek :
I I I. Erreferentzi sistema
Espazioan O puntua hartzen bada, planoko P puntu bakoitzari OP bektorea dagokio, hain zuzen ere, O jatorri puntua P puntu horrekin elkartzen duena. bektore horri P puntuaren posizio bektore deritzo. Horrez gainera,
bektore horri P puntuaren posizio bektore deritzo. Horrez gainera,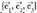 oinarria baldin badaukagu, bektore bakoitzari hiru zenbaki dagozkio, bere koordenatuak hain zuzen ere ; beraz,
oinarria baldin badaukagu, bektore bakoitzari hiru zenbaki dagozkio, bere koordenatuak hain zuzen ere ; beraz,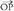 bektoreari hau dagokio :
bektoreari hau dagokio : Espazioko P puntuari hiru zenbaki erreal dagozkio, bere koordenatuak hain zuzen ere eta era honetan adierazten da :
Espazioko P puntuari hiru zenbaki erreal dagozkio, bere koordenatuak hain zuzen ere eta era honetan adierazten da :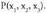 Hiru dimentsiotako bektore espazioaren jatorriaren eta oinarriaren multzoak espazioko erreferentzi sistema eratzen duela esaten da.
Hiru dimentsiotako bektore espazioaren jatorriaren eta oinarriaren multzoak espazioko erreferentzi sistema eratzen duela esaten da.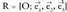 erreferentzi sistema definituta, ondoko elkarrekikotasunak ditugu :
erreferentzi sistema definituta, ondoko elkarrekikotasunak ditugu : Jatorri puntutik igaro eta oinarriko bektoreen norabideak dituzten zuzenak koordenatu sistemaren ardatzak dira. Normalean erabiltzen den erreferentziak oinarri bektoreak ortonormalak edo cartesiarrak izaten ditu. Oinarri horretako hiru ardatzak,
Jatorri puntutik igaro eta oinarriko bektoreen norabideak dituzten zuzenak koordenatu sistemaren ardatzak dira. Normalean erabiltzen den erreferentziak oinarri bektoreak ortonormalak edo cartesiarrak izaten ditu. Oinarri horretako hiru ardatzak,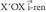 arabera doana,
arabera doana,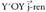 arabera doana eta
arabera doana eta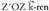 arabera doana adierazten dira. Besterik esaten ez den bitartean behintzat, oinarriko bektoreak ortonormalak direla hartzen da
arabera doana adierazten dira. Besterik esaten ez den bitartean behintzat, oinarriko bektoreak ortonormalak direla hartzen da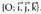 Bi puntu elkartzen dituen bektorea.
Bi puntu elkartzen dituen bektorea. puntuak emanda, beren posizio bektoreek hau betetzen dute :
puntuak emanda, beren posizio bektoreek hau betetzen dute :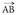 da puntu horiek elkartzen dituen bektorea. Beraz,
da puntu horiek elkartzen dituen bektorea. Beraz,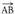 bektoreak honako koordenatu hauek ditu :
bektoreak honako koordenatu hauek ditu :
Zuzenki baten erdiko puntua.
A eta B muturtzat dituen zuzenkiaren erdiko M puntua kalkulatzeko,
ondorengoa erabil dezakegu :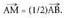 Horren ondorioz :
Horren ondorioz :
Zatitu zuzenki bat hiru zati berdin edo gehiagotan.
AB zuzenkia hiru zati berdin edo gehiagotan zatitzen duten puntuak kalkulatzeko, abiapuntua zera da, AB herenetan zatitzen duten puntuak zuzenkiaren muturretako batetik heren batera edo bi herenetara
egongo dira.
puntuak zuzenkiaren muturretako batetik heren batera edo bi herenetara
egongo dira. Koordenatuak erabiliz, hau ateratzen da :
Koordenatuak erabiliz, hau ateratzen da :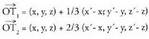 AB zuzenkia n zati berdinetan zatitu nahi baldin bada, bera zatitzen
duten n-1 puntuak era honetan lortzen dira :
AB zuzenkia n zati berdinetan zatitu nahi baldin bada, bera zatitzen
duten n-1 puntuak era honetan lortzen dira :
Puntu batekiko simetrikoa den beste bat.
A-ren M-rekiko puntu simetrikoa, S puntua da eta M puntua AS
zuzenkiaren erdiko puntua da. S puntua aurkitzeko, A(x, y, z) eta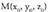 badira eta simetrikoa
badira eta simetrikoa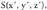 honako hau beteko da :
honako hau beteko da :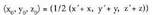 Puntu simetrikoaren koordenatuak diren
Puntu simetrikoaren koordenatuak diren askatuz, hau gelditzen da :
askatuz, hau gelditzen da :
- Ariketak
3. a) Kalkulatu A(1, 2, -1) eta B(5, 6, 3) puntuak elkartzen dituen bektorearen osagaiak.b) Kalkulatu AB zuzenkia lau zati berdinetan zatitzen dituen puntuen koordenatuak.4. Kalkulatu A(-3, 1, 2) puntuak (1, 2, -1) puntuarekiko duen puntu simetrikoaren koordenatuak.5. Kalkulatu P(x,y z) puntuak jatorriarekiko duen puntu simetrikoaren koordenatuak.
IV. Zuzena espazioan.
Zuzena ondo zehaztuta gelditzen da, baldin eta igarotzen den puntuetako bat eta duen norabidea ezagutzen badira. Beraz, zuzena igarotzen den puntua eta
puntua eta norabide bektorea ezagutzen baditugu, bere ekuazioa kalkuia daiteke. Ekuazio horrek, tankera baliokide gehiago ere izan ditzake.
norabide bektorea ezagutzen baditugu, bere ekuazioa kalkuia daiteke. Ekuazio horrek, tankera baliokide gehiago ere izan ditzake.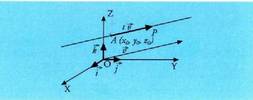
Bektore ekuazioa:
Zuzenaren puntuetako bat P(x, y, z) izango da eta bere posizio bektorea bektoreaz adierazten bada, ondorengoa bete behar du :
bektoreaz adierazten bada, ondorengoa bete behar du : Non
Non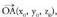 , ezaguna den A puntuaren posizio bektorea den eta
, ezaguna den A puntuaren posizio bektorea den eta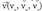 zuzen horren norabide bektorea.t parametroa kopuru erreala da, eta balio desberdinak ematen
zaizkio zuzenaren puntuak lortzeko. Alderantziz, zuzeneko puntu
batek emandako ekuazioa bete egingo du t parametroaren balioren
batentzat.Adibidea:A(1, 0, 1) puntutik igarotzen den eta
zuzen horren norabide bektorea.t parametroa kopuru erreala da, eta balio desberdinak ematen
zaizkio zuzenaren puntuak lortzeko. Alderantziz, zuzeneko puntu
batek emandako ekuazioa bete egingo du t parametroaren balioren
batentzat.Adibidea:A(1, 0, 1) puntutik igarotzen den eta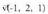 norabide- 'bektorea duen zuzena honako hau da :
norabide- 'bektorea duen zuzena honako hau da :
Parametro ekuazioak :
Zuzenaren parametro ekuazioak bektore ekuaziotik lortzen dira
hiru koordenatuen arabera hiru ekuazioetan deskonposatuz: Adibidea : Ipini aurreko ekuazioa parametro ekuazio tankeran.
Adibidea : Ipini aurreko ekuazioa parametro ekuazio tankeran.
Ekuazio jarraia :
Ekuazio jarraia aurreko ekuazioetatik parametroa desagertarazita
lortzen da.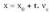 baldin bada, t askatuta, honako hau lortzen da.
baldin bada, t askatuta, honako hau lortzen da.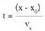 y eta z-rekin ere berdin eginda eta t-ren balioak berdinduta, ekuazio
jarrai hau lortzen da :
y eta z-rekin ere berdin eginda eta t-ren balioak berdinduta, ekuazio
jarrai hau lortzen da :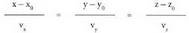 Adibidea :Aurreko bi adibideetako zuzenaren ekuazio jarraia honako hau
da :
Adibidea :Aurreko bi adibideetako zuzenaren ekuazio jarraia honako hau
da : Zuzen bat ongi zehaztuta dago bere puntuetako bi ezagutzen baditugu. Datu hauek aurrekoen baliokideak dira, izan ere, A eta B puntuak ezagutzen baditugu, puntu bat bederen ezaguna da, A adibidez, eta zuzenaren norabide bektorea, A eta B elkartzen dituen
Zuzen bat ongi zehaztuta dago bere puntuetako bi ezagutzen baditugu. Datu hauek aurrekoen baliokideak dira, izan ere, A eta B puntuak ezagutzen baditugu, puntu bat bederen ezaguna da, A adibidez, eta zuzenaren norabide bektorea, A eta B elkartzen dituen alegia.
alegia.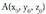 eta
eta puntuetatik igarotzen dela dakigun zuzenaren ekuazioa kalkulatzeko, A puntu ezaguntzat hartuko dugu eta
puntuetatik igarotzen dela dakigun zuzenaren ekuazioa kalkulatzeko, A puntu ezaguntzat hartuko dugu eta berriz norabide bektoretzat :
berriz norabide bektoretzat :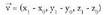 Datu hauekin aurreko ekuazio guztiak lor daitezke.Adibidea :1. Kalkulatu A(1, -1, 2) eta B(0, 1, -1) puntuetatik igarotzen den zuzenaren ekuazioa. Puntu bat hartu, A(1, -1, 2) adibidez eta
Datu hauekin aurreko ekuazio guztiak lor daitezke.Adibidea :1. Kalkulatu A(1, -1, 2) eta B(0, 1, -1) puntuetatik igarotzen den zuzenaren ekuazioa. Puntu bat hartu, A(1, -1, 2) adibidez eta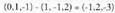 bektorea ere hartuko dugu.Bektore ekuazioa: (x, y, z) = (1, -1,2) + t(-1,2,-3)Parametro ekuazioak :
bektorea ere hartuko dugu.Bektore ekuazioa: (x, y, z) = (1, -1,2) + t(-1,2,-3)Parametro ekuazioak :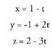 Ekuazio jarraia :
Ekuazio jarraia :
Zuzena bi planoen ebakidura gisa.
Zuzena halaber bi planoen ebakidura moduan ere defini daiteke.
Zuzenaren ekuazioa emateko modu hau aurrerago aztertuko da, bi
planoen arteko posizio erlatiboak ikusten direnean. Hala ere ordea,
maiz samar aurkitzen den modua delako, hemen aipatzeak ere
merezi du.Planoak honako adierazpen modu hau izaten du ekuaziotzat : Ax
+ By + Cz + D = 0 ; A, B, C eta D zenbaki errealak izanik eta x, y eta
z ezezagunak, planokoa den puntu baten koordenatuak izanik.Orokorki, zuzen bat bi ekuazioen multzoa da :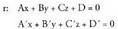 non x, y eta z-ren koefizienteak, aurrerago ikusiko den bezala,
ezin daitezkeen denak proportzionalak izan.
non x, y eta z-ren koefizienteak, aurrerago ikusiko den bezala,
ezin daitezkeen denak proportzionalak izan. Adibidea :Kalkula itzazu ardatz koordenatuen ekuazioak.Hiru ardatz koordenatuak, jatorri puntutik igaro eta norabide
bektore ezaguna dutenak dira. Beren ekuazioak honako hauek dira :OX ardatza : Zuzen horretakoa den puntuetako bat
Adibidea :Kalkula itzazu ardatz koordenatuen ekuazioak.Hiru ardatz koordenatuak, jatorri puntutik igaro eta norabide
bektore ezaguna dutenak dira. Beren ekuazioak honako hauek dira :OX ardatza : Zuzen horretakoa den puntuetako bat da eta zuzen horren norabide bektoreetako bat berriz,
da eta zuzen horren norabide bektoreetako bat berriz,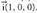 Bektore ekuazioa : (x, y, z) = t (1, 0, 0)Parametro ekuazioak :
Bektore ekuazioa : (x, y, z) = t (1, 0, 0)Parametro ekuazioak :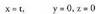 Era berean, y = 0 eta z = 0 planoen ebakidura gisa ere har daiteke.OY ardatza: Zuzen horretakoa den puntuetako bat
Era berean, y = 0 eta z = 0 planoen ebakidura gisa ere har daiteke.OY ardatza: Zuzen horretakoa den puntuetako bat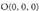 da eta zuzen horren norabide bektoreetako bat berriz,
da eta zuzen horren norabide bektoreetako bat berriz,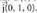 Bektore ekuazioa : (x, y, z) = t (0, 1, 0)Parametro ekuazioak :
Bektore ekuazioa : (x, y, z) = t (0, 1, 0)Parametro ekuazioak : Era berean, x = 0 eta z = 0 planoen ebakidura gisa ere har daiteke.OZ ardatza: Zuzen horretakoa den puntuetako bat
Era berean, x = 0 eta z = 0 planoen ebakidura gisa ere har daiteke.OZ ardatza: Zuzen horretakoa den puntuetako bat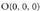 da eta zuzen horren norabide bektoreetako bat berriz,
da eta zuzen horren norabide bektoreetako bat berriz, Bektore ekuazioa : (x, y, z) = t (O, 0, 1)Parametro ekuazioak :
Bektore ekuazioa : (x, y, z) = t (O, 0, 1)Parametro ekuazioak :
- Ariketak
6. Kalkula itzazu P (-1, -1, 0) puntutik igaro eta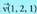
Puntuaren eta zuzenaren artekoak.
r zuzena bere ekuazioarekin eta P puntua bere koordenatuekin
emanda, puntua, zuzenekoa edota zuzenaz kanpokoa izan daiteke :- Puntua zuzenekoa da, baldin eta puntuaren koordenatuek zuzenaren
ekuazioak betetzen badituzte.- Puntua ez da zuzenekoa edota zuzenaz kanpokoa da, baldin eta
puntuaren koordenatuek zuzenaren ekuazioak betetzen ez badituzte
.Zuzenaren ekuazioa parametro edo bektore moduan baldin badago,
puntuak ekuazioak beteko ditu baldin eta bere koordenatuentzat,
beteko dituen t parametroaren balio bakarra kalkulatzen bada.
Hau da:P(a, b, c) puntuak beteko du r zuzenaren ekuazioa, baldin eta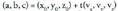 t-ren balioren batentzat betetzen bada.
t-ren balioren batentzat betetzen bada.
Edota t-ren b 'o berberarentzat ondoko hauek betetzen badira :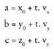 Zuzena ekuazio jarraiaren bidez emanda badator, edota bi planoren
ebakidura moduan, puntuaren koordenatuek bi ekuazioak bete
behar dituzte :
Zuzena ekuazio jarraiaren bidez emanda badator, edota bi planoren
ebakidura moduan, puntuaren koordenatuek bi ekuazioak bete
behar dituzte :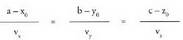 edota,
edota,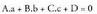 eta
eta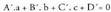 Adibidea:1. A(3, 2, -4) eta B(2, 1, -2) puntuak zuzenekoak badira,
Adibidea:1. A(3, 2, -4) eta B(2, 1, -2) puntuak zuzenekoak badira,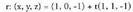 t-ren balioren batentzat bete beharko da :(3, 2,-4) = (1, 0, -1) + t(1, 1,-1),hauda,3=1+t,2=0+t,-4=-1-t.Lehenengo ekuazioak t = 2 du emaitza, bigarrenak ere bai, baina hirugarrenak t = 3 du ; beraz,
t-ren balioren batentzat bete beharko da :(3, 2,-4) = (1, 0, -1) + t(1, 1,-1),hauda,3=1+t,2=0+t,-4=-1-t.Lehenengo ekuazioak t = 2 du emaitza, bigarrenak ere bai, baina hirugarrenak t = 3 du ; beraz,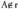 (A ez da r-koa).(2,1,-2)=(1,0,-1)+t(1,1,-1),hauda,2=1+t, 1=O+t,-2=-1-t.Hiru ekuazioak ere, t = 1 denean betetzen dira ; beraz,
(A ez da r-koa).(2,1,-2)=(1,0,-1)+t(1,1,-1),hauda,2=1+t, 1=O+t,-2=-1-t.Hiru ekuazioak ere, t = 1 denean betetzen dira ; beraz,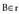 (B, r- koa da).r zuzenaren ekuazioak ezagutzen direnean, zuzen horretako
puntu bat jakin nahi baldin bada, nahikoa da t parametroari balio
bat ematea puntuaren koordenatuak lortzeko. Ekuazioak jarraiak
badira, edota bi planoen ebakidura modukoak, koordenatu bati
hautazko balio bat ematen zaio, x adibidez, eta beste biak kalkulatzen
dira, y eta z kasu honetan.Adibidez:Kalkulatu ondorengo ekuazioa duen zuzenekoa den puntu bat :
(B, r- koa da).r zuzenaren ekuazioak ezagutzen direnean, zuzen horretako
puntu bat jakin nahi baldin bada, nahikoa da t parametroari balio
bat ematea puntuaren koordenatuak lortzeko. Ekuazioak jarraiak
badira, edota bi planoen ebakidura modukoak, koordenatu bati
hautazko balio bat ematen zaio, x adibidez, eta beste biak kalkulatzen
dira, y eta z kasu honetan.Adibidez:Kalkulatu ondorengo ekuazioa duen zuzenekoa den puntu bat :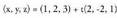 t = 1 hartuta, hau gelditzen da: (x, y, z) = (l, 2, 3) + 1(2, -2, 1) = (3, 0, 4)Soilena halere t = 0 hartzea da eta orduan (x, y, z) = (1, 2, 3) da.Kalkulatu ondoko ekuazioa duen zuzeneko punturen bat :
t = 1 hartuta, hau gelditzen da: (x, y, z) = (l, 2, 3) + 1(2, -2, 1) = (3, 0, 4)Soilena halere t = 0 hartzea da eta orduan (x, y, z) = (1, 2, 3) da.Kalkulatu ondoko ekuazioa duen zuzeneko punturen bat :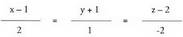
- Ariketak
8. Esazu ea (3, -2, 2) puntua r: (x, y, z) = (-1, 2, 0) + t(2, - 2, 1) zuzenekoa den.9. Esazu ea (4, -1, 3) puntua r : (x - 1)l3 = (y + 3)/2 = (z - 1)/(-2) zuzenekoa den.
V. Bi zuzenen arteko posizio erlatiboak. z=1-t
Espazioko bi zuzenen ekuazioak emanda, beren posizio erlatiboa jakiteko, zuzen bakoitzaren puntu bat eta berorren norabide bektorea ateraz hasi behar da. Bitez r zuzena, norabide bektoreduna eta A puntutik igarotzen dena eta s zuzena,
norabide bektoreduna eta A puntutik igarotzen dena eta s zuzena, norabide bektoreduna eta B puntutik igarotzen dena. Elkarrekiko posizio aukerak hauek dira :- Bi zuzenek norabide berbera baldin badute, hots,
norabide bektoreduna eta B puntutik igarotzen dena. Elkarrekiko posizio aukerak hauek dira :- Bi zuzenek norabide berbera baldin badute, hots, baldin bada, bi aukera daude :a)
baldin bada, bi aukera daude :a) (A ez da s-koa) eta orduan, ez dute puntu komunik eta zuzenak paraleloak dira.b)
(A ez da s-koa) eta orduan, ez dute puntu komunik eta zuzenak paraleloak dira.b) (A s-koa da), eta orduan bi zuzenek puntu guztiak komunak dituzte. Zuzenak bat datoz beraz, zuzen bakarra da.- Bi zuzenek norabide berbera ez baldin badute :a) Biek punturen bat komuna badute, orduan elkar ebakitzen
dute.b) Biek puntu komunik ez badute, orduan elkar gurutzatzen
dute.Espazioan, planoan baino kasu bat gehiago dago, izan ere, puntu
komunik ez duten bi zuzen, paraleloak bakarrik izan daitezke plano
berekoak badira, baina espazioan plano berean ez badaude gurutzatu
ere egin daitezke.
(A s-koa da), eta orduan bi zuzenek puntu guztiak komunak dituzte. Zuzenak bat datoz beraz, zuzen bakarra da.- Bi zuzenek norabide berbera ez baldin badute :a) Biek punturen bat komuna badute, orduan elkar ebakitzen
dute.b) Biek puntu komunik ez badute, orduan elkar gurutzatzen
dute.Espazioan, planoan baino kasu bat gehiago dago, izan ere, puntu
komunik ez duten bi zuzen, paraleloak bakarrik izan daitezke plano
berekoak badira, baina espazioan plano berean ez badaude gurutzatu
ere egin daitezke.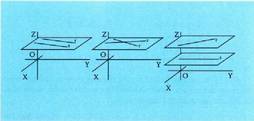 Adibidea:1. Ondoko zuzen hauek emanda :
Adibidea:1. Ondoko zuzen hauek emanda :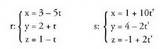 aztertu elkarrekiko duten posizio erlatiboa.Norabide bektoreak
aztertu elkarrekiko duten posizio erlatiboa.Norabide bektoreak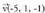 eta
eta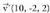 dira. Bigarrena, lehenengoa bider -2 da ; beraz,
dira. Bigarrena, lehenengoa bider -2 da ; beraz, Orduan, paraleloak edota bat bera dira.Lehen zuzeneko A(3, 2, 1) puntua, bigarren zuzenekoa ere ba ote
den jakin nahi da :
Orduan, paraleloak edota bat bera dira.Lehen zuzeneko A(3, 2, 1) puntua, bigarren zuzenekoa ere ba ote
den jakin nahi da :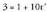 izanik,
izanik,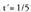 du emaitza, baina y= 4 - 2(1/5) = 18/5 2 ; beraz,
du emaitza, baina y= 4 - 2(1/5) = 18/5 2 ; beraz, (A ez da s-koa). Orduan, zuzenak paraleloak dira.2. Ondoko zuzena hauek emanda :
(A ez da s-koa). Orduan, zuzenak paraleloak dira.2. Ondoko zuzena hauek emanda :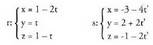 aztertu beren elkarrekiko posizio erlatiboa.Norabide bektoreak,
aztertu beren elkarrekiko posizio erlatiboa.Norabide bektoreak,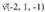 eta
eta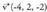 dira. Bigarrena, lehenengoa 2-z biderkatuta lor daiteke :
dira. Bigarrena, lehenengoa 2-z biderkatuta lor daiteke : beraz, paraleloak edota bat bera dira. r zuzenekoa den puntuetako bat A(1, 0, 1) da.
beraz, paraleloak edota bat bera dira. r zuzenekoa den puntuetako bat A(1, 0, 1) da.
A s-koa ere baden jakiteko,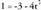 ekuazioak duen emaitza ikusiko dugu. Kasu honetan
ekuazioak duen emaitza ikusiko dugu. Kasu honetan da emaitza eta hori ordezkatuz, y = 2 + 2(-1) = 0 da ; z-dunean ordezkatuz berriz : z = -1 - 2(-1) = 1.
da emaitza eta hori ordezkatuz, y = 2 + 2(-1) = 0 da ; z-dunean ordezkatuz berriz : z = -1 - 2(-1) = 1.
Beraz, A(1, 0, 1) puntua, s zuzenaren ekuazioan parametroaren -1 balioarentzako bete egiten da ; beraz, (A s-koa da) eta r eta s zuzenak bat bera dira.3. Ondorengo zuzenak emanik :
(A s-koa da) eta r eta s zuzenak bat bera dira.3. Ondorengo zuzenak emanik :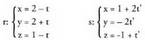 aztertu beren arteko posizio erlatiboa.Norabide bektoreak
aztertu beren arteko posizio erlatiboa.Norabide bektoreak eta
eta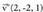 dira. Beraz, ez dira proportzionalak eta horren ondorioz ez dira paraleloak. Orduan, elkar ebaki edota gurutzatu egingo dute. Puntu komun bat baldin badute, elkar ebakiko dute. Ebakitzeko, lehen zuzeneko t-ren balioren batek eta bigarren zuzeneko C-ren beste batek, balio berberak eman behar dizkiete x, y, z-ri bi ekuazio segidetan. Bi zuzenekin jardutean, oso garrantzitsua da bietako parametroei izen desberdinak ematea, nahasketarik izan ez dadin. Esandakoaren arabera, ondoko ekuazio hauek ateratzen dira :
dira. Beraz, ez dira proportzionalak eta horren ondorioz ez dira paraleloak. Orduan, elkar ebaki edota gurutzatu egingo dute. Puntu komun bat baldin badute, elkar ebakiko dute. Ebakitzeko, lehen zuzeneko t-ren balioren batek eta bigarren zuzeneko C-ren beste batek, balio berberak eman behar dizkiete x, y, z-ri bi ekuazio segidetan. Bi zuzenekin jardutean, oso garrantzitsua da bietako parametroei izen desberdinak ematea, nahasketarik izan ez dadin. Esandakoaren arabera, ondoko ekuazio hauek ateratzen dira :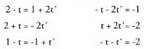 t eta
t eta -aren balioak kalkulatzeko, ekuazio sistema edozein metodoz ebatz daiteke eta emaitzarik badagoen ala ez ikusi, baina soilena, Rouche-ren teorema erabiltzea da :Horretarako, koefizienteen A matrizea idazten da, eta baita A'
matrize zabaldua ere :
-aren balioak kalkulatzeko, ekuazio sistema edozein metodoz ebatz daiteke eta emaitzarik badagoen ala ez ikusi, baina soilena, Rouche-ren teorema erabiltzea da :Horretarako, koefizienteen A matrizea idazten da, eta baita A'
matrize zabaldua ere :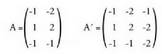 Matrizea errenkadaka edota zutabeka elkarrekin ipinitako bektore sorta moduan hartuta, linealki aske agertzen den bektore kopuruari matrizearen hein deritzo. A-ren heina 2 da, izan ere, bi zutabeak, bi norabide bektoreak baitira, lehendik ere ikusia baita linealki askeak direla.
Matrizea errenkadaka edota zutabeka elkarrekin ipinitako bektore sorta moduan hartuta, linealki aske agertzen den bektore kopuruari matrizearen hein deritzo. A-ren heina 2 da, izan ere, bi zutabeak, bi norabide bektoreak baitira, lehendik ere ikusia baita linealki askeak direla. -aren heina jakiteko, determinantea kalkulatzea da biderik zuzenena :
-aren heina jakiteko, determinantea kalkulatzea da biderik zuzenena :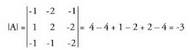 Determinantea zeroren desberdina da ; beraz, bektoretzat hartutako
hiru errenkadak edo zutabeak, zenbaki hirukoteak, linealki askeak
dira.A-ren heina 2 da eta
Determinantea zeroren desberdina da ; beraz, bektoretzat hartutako
hiru errenkadak edo zutabeak, zenbaki hirukoteak, linealki askeak
dira.A-ren heina 2 da eta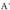 -rena berriz 3. Horrek esan nahi du, gai askeak ezin lor daitezkeela koefizienteen konbinazio lineal moduan ; beraz, ezin daiteke aurkitu hiru ekuazioak betetzen dituzten t eta
-rena berriz 3. Horrek esan nahi du, gai askeak ezin lor daitezkeela koefizienteen konbinazio lineal moduan ; beraz, ezin daiteke aurkitu hiru ekuazioak betetzen dituzten t eta -aren baliorik. Ez dago beraz bi zuzenentzat komuna den punturik ; zuzenek orduan, elkar gurutzatzen dute.4. Ondoko zuzen hauek emanik :
-aren baliorik. Ez dago beraz bi zuzenentzat komuna den punturik ; zuzenek orduan, elkar gurutzatzen dute.4. Ondoko zuzen hauek emanik :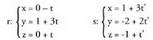 aztertu beren posizio erlatiboa.
aztertu beren posizio erlatiboa.
Norabide bektoreak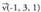 eta
eta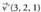 dira. Linealki askeak dira ; beraz, elkar ebaki edota gurutzatzen duten zuzenak dira.
dira. Linealki askeak dira ; beraz, elkar ebaki edota gurutzatzen duten zuzenak dira.
Sistema ebatzita: Koefizienteen A matrizea eta gai askeekin handitutako
Koefizienteen A matrizea eta gai askeekin handitutako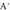 matrize zabaldua honako hauek dira :
matrize zabaldua honako hauek dira :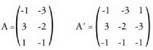 A-ren heina 2 da, izan ere, zutabeak, zuzenen norabide bektoreak baitira, bigarrena zeinua aldatuta izanik.
A-ren heina 2 da, izan ere, zutabeak, zuzenen norabide bektoreak baitira, bigarrena zeinua aldatuta izanik.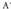 -aren heina kalkulatzeko, bere determinantea kalkulatzen da :
-aren heina kalkulatzeko, bere determinantea kalkulatzen da :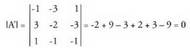 Beraz, hirugarren zutabea, lehenengo bien konbinazio lineala da eta sistemak emaitza badu. Puntuaren koordenatuak jakin nahi badira, sistema ebatzi behar da. Adibidez, azkeneko ekuazioaren kasuan,
Beraz, hirugarren zutabea, lehenengo bien konbinazio lineala da eta sistemak emaitza badu. Puntuaren koordenatuak jakin nahi badira, sistema ebatzi behar da. Adibidez, azkeneko ekuazioaren kasuan,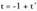 lortzen da eta aurreko ekuazioan ordezkatuz :
lortzen da eta aurreko ekuazioan ordezkatuz :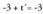 da; beraz,
da; beraz, zero da, eta ebaki puntua A(1, -2, -1).Bi zuzen paraleloak diren, elkar gurutzatzen duten ala elkar ebakitzen
duten jakiteko modu hau, oso erraza da norabide bektoreak
ezagutuz gero, eta norabide bektoreak erraz kalkulatzen dira zuzenak
ekuazio jarraien, bektore ekuazioen edota parametro ekuazioen
bitartez emanak baldin badaude. Zuzenak ordea, bi planoren ebakidura
moduan ere eman daitezke :
zero da, eta ebaki puntua A(1, -2, -1).Bi zuzen paraleloak diren, elkar gurutzatzen duten ala elkar ebakitzen
duten jakiteko modu hau, oso erraza da norabide bektoreak
ezagutuz gero, eta norabide bektoreak erraz kalkulatzen dira zuzenak
ekuazio jarraien, bektore ekuazioen edota parametro ekuazioen
bitartez emanak baldin badaude. Zuzenak ordea, bi planoren ebakidura
moduan ere eman daitezke : Kasu honetan erosoagoa izan ohi da lau ekuazio eta hiru ezezagun
dituen ekuazio sistema moduan planteatzea. Koefizienteen matrizea
eta gai askeekin handitutako matrize zabaldua, ondoko hauek
izango dira :
Kasu honetan erosoagoa izan ohi da lau ekuazio eta hiru ezezagun
dituen ekuazio sistema moduan planteatzea. Koefizienteen matrizea
eta gai askeekin handitutako matrize zabaldua, ondoko hauek
izango dira :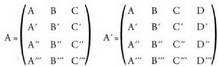 Zuzena definitzen dutenak elkar ebakitzen duten planoak direlako, A-ren heina 2 edo handiagoa da.
Zuzena definitzen dutenak elkar ebakitzen duten planoak direlako, A-ren heina 2 edo handiagoa da.
Bi zuzenek espazioan:
- Ez dute puntu komunik [A-ren heina  -aren heina baino] , eta kasu horretan, planoan ez bezala, bi aukera daude:a) Bi zuzenek norabide berbera izatea, eta orduan paraleloak izango dira. [A-ren heina = 2]
b) Norabide desberdinak izatea, eta orduan elkar gurutzatzen dute espazioan. [A-ren heina = 3].
-aren heina baino] , eta kasu horretan, planoan ez bezala, bi aukera daude:a) Bi zuzenek norabide berbera izatea, eta orduan paraleloak izango dira. [A-ren heina = 2]
b) Norabide desberdinak izatea, eta orduan elkar gurutzatzen dute espazioan. [A-ren heina = 3].
1 1 m 1 1 m 3- Puntu komunak dituzte eta orduan :a) Punu komun bakarra baldin badute, elkar ebakitzen dute. [Aren heina = -aren heina = 3].b) Puntu guztiak komunak badituzte, orduan bat datoz eta lerro berbera dira. [A-ren heina =
-aren heina = 3].b) Puntu guztiak komunak badituzte, orduan bat datoz eta lerro berbera dira. [A-ren heina = -ren heina = 2].Horrela planteatuta, arazoa, ekuazio sistema baten emaitzak
interpretatzera edo ulertzera mugatzen da.Adibidea:Kalkula ezazu m-ren balioa, ondoko zuzenek puntu batean elkar
ebaki dezaten :
-ren heina = 2].Horrela planteatuta, arazoa, ekuazio sistema baten emaitzak
interpretatzera edo ulertzera mugatzen da.Adibidea:Kalkula ezazu m-ren balioa, ondoko zuzenek puntu batean elkar
ebaki dezaten : Zuzenak planoen ebakidura bidez emanak datoz. Bi zuzenen ebaki puntuak, baldin badago, r zuzenaren bi ekuazioak eta s zuzenaren biak bete behar ditu. Hau da, puntu batean ebakiko dute elkar, baldin eta ekuazio horiek emaitza bat bakarra baldin badute.
Zuzenak planoen ebakidura bidez emanak datoz. Bi zuzenen ebaki puntuak, baldin badago, r zuzenaren bi ekuazioak eta s zuzenaren biak bete behar ditu. Hau da, puntu batean ebakiko dute elkar, baldin eta ekuazio horiek emaitza bat bakarra baldin badute.
Hori gerta dadin, koefizienteekin eratutako A matrizearen heina eta gai askeekin osatutako matrize zabalduarena, berdinak izan behar dute eta 3 balio behar dute.
matrize zabalduarena, berdinak izan behar dute eta 3 balio behar dute. Lehenengo hiru errenkadak hartzen badira, horiek ez dira m-ren
baitakoak :
Lehenengo hiru errenkadak hartzen badira, horiek ez dira m-ren
baitakoak :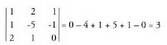 Beraz, A-ren heina 3 da.
Beraz, A-ren heina 3 da.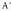 berriz zutabe bat gehiagorekin zabaldutako matrizea da; beraz, sistema bateragarria eta zehatza den ikusteko, 4x4 erakoa den matrizearen determinantea kalkulatu beharko litzateke eta zero egiten duen m-ren balioa aurkitu. Lau errenkada eta lau zutabe dituen matrizearen determinantea kalkulatzeko, errenkada edo zutabe bateko elementuak, beren adjuntuez biderkatu behar dira eta emaitzak batu. Horrek, 3x3 erako lau determinante kalkulatu behar direla esan nahi du. Prozedura nekeza da, eta erosoago izan ohi da egiteko beste moduren bat. Kasu honetan, lehen hiru ekuazioek eratutako sistema adibidez Cramer-en metodoz ebatzi eta x = 1, y = 0, z = 1 emaitza lortzen da.Gero, laugarren ekuazioan x, y eta z-ren balio horiek ordezkatu
eta honako hau gelditzen da :
berriz zutabe bat gehiagorekin zabaldutako matrizea da; beraz, sistema bateragarria eta zehatza den ikusteko, 4x4 erakoa den matrizearen determinantea kalkulatu beharko litzateke eta zero egiten duen m-ren balioa aurkitu. Lau errenkada eta lau zutabe dituen matrizearen determinantea kalkulatzeko, errenkada edo zutabe bateko elementuak, beren adjuntuez biderkatu behar dira eta emaitzak batu. Horrek, 3x3 erako lau determinante kalkulatu behar direla esan nahi du. Prozedura nekeza da, eta erosoago izan ohi da egiteko beste moduren bat. Kasu honetan, lehen hiru ekuazioek eratutako sistema adibidez Cramer-en metodoz ebatzi eta x = 1, y = 0, z = 1 emaitza lortzen da.Gero, laugarren ekuazioan x, y eta z-ren balio horiek ordezkatu
eta honako hau gelditzen da :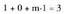
Rouche-ren teorema. Heina.
Heina : Errenkada berean dauden zenbakiak bektore baten osagai gisa
hartzen badira, orduan matrizeak dituen errenkada linealki askeen kopurua
da heina. Era berean lortzen da errenkaden ordez zutabeak erabiliz kalkulatuta
.Adibidea:A matrizea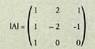 Bektoretzat hartutako errenkadak, (1,2,1),(1,-2,1) eta (1,0,0) dira.Hirugarren lerroa, bi aurrekoen baturaren erdia da ; beraz, horren heina 2
da. Zutabeak hartuta berriz, bigarrena hirugarrenaren bikoitza da ; beraz,
linealki aske diren zutabeetako bektoreen kopurua ere bikoa da.Matrize karratu baten heina kalkulatzeko, bere determinantea zero ez
dela erabil daiteke, baldin eta osatzen duten errenkadetako bektoreak linealki
askeak badira.m ekuazio n ezezagunekin dituzten sistemen ebazgarritasuna eztabaidatzeko,
Rouche-ren teorema erabiltzen da :Bedi honako sistema hau :
Bektoretzat hartutako errenkadak, (1,2,1),(1,-2,1) eta (1,0,0) dira.Hirugarren lerroa, bi aurrekoen baturaren erdia da ; beraz, horren heina 2
da. Zutabeak hartuta berriz, bigarrena hirugarrenaren bikoitza da ; beraz,
linealki aske diren zutabeetako bektoreen kopurua ere bikoa da.Matrize karratu baten heina kalkulatzeko, bere determinantea zero ez
dela erabil daiteke, baldin eta osatzen duten errenkadetako bektoreak linealki
askeak badira.m ekuazio n ezezagunekin dituzten sistemen ebazgarritasuna eztabaidatzeko,
Rouche-ren teorema erabiltzen da :Bedi honako sistema hau :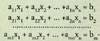 Matrize zabaldua berriz :
Matrize zabaldua berriz : Matrize zabaldua berriz :
Matrize zabaldua berriz : Rouche-ren teoremaren arabera, A-ren heina =
Rouche-ren teoremaren arabera, A-ren heina = aren heina = n =
ezezagun kopurua baldin bada, sistema, bateragarria eta zehatza da, hau
da, bt emaitza bakar ditu.A-ren heina =
aren heina = n =
ezezagun kopurua baldin bada, sistema, bateragarria eta zehatza da, hau
da, bt emaitza bakar ditu.A-ren heina = -aren heina e n baino baldin bada, sistema bateragarri zehazgabea da, eta emaitza kopuru infinitua du. Emaitzak lortzeko behar diren parametroen kopurua, ezezagun kopurua ken heina izango da.
-aren heina e n baino baldin bada, sistema bateragarri zehazgabea da, eta emaitza kopuru infinitua du. Emaitzak lortzeko behar diren parametroen kopurua, ezezagun kopurua ken heina izango da.
A-ren heina
Puntu batetik igaro eta beste zuzen bati buruz paraleloa den zuzena.
Puntu batetik igaro eta beste zuzen bati buruz paraleloa den zuzenaren
ekuazioa kalkulatzeko, zuzen paraleloak norabide bektorea
beste zuzenarekiko proportzionala duelako printzipioa erabiltzen da.Adibidea : Kalkula ezazu P(-2,3,0) puntutik igaro eta (x,y,z)=
_ (1,-1,-1)+t(1,3,4) ekuaziodun r zuzenari buruz paraleloa den
zuzenaren ekuazioa.Zuzen paraleloaren norabide bektoretzat,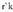 duen bektore berbera hartzen da eta zuzen paraleloak honako ekuazio hau duela ateratzen da :
duen bektore berbera hartzen da eta zuzen paraleloak honako ekuazio hau duela ateratzen da :
- Ariketak
10. Azter itzazu bi zuzen hauen posizio erlatiboak : 11. 3 dimentsioko euklidear espazio batean eta OXYZ erreferentzia ortonormala izanda, ondoko zuzenon ekuazioak ematen dira:
11. 3 dimentsioko euklidear espazio batean eta OXYZ erreferentzia ortonormala izanda, ondoko zuzenon ekuazioak ematen dira: Frogatu hiru zuzenek puntu komun bat badutela eta kalkulatu
puntu horren koordenatuak.12. Kalkulatu jatorri puntutik igaroz
Frogatu hiru zuzenek puntu komun bat badutela eta kalkulatu
puntu horren koordenatuak.12. Kalkulatu jatorri puntutik igaroz
VI. Planoa.
Planoa zehaztuta dago baldin eta puntu bat eta beren artean paraleloak
ez diren eta planoari buruz paraleloak diren bi norabide ezagutzen
badira. Halaber zehaztuta dago baldin eta planoan dauden
zuzen bat eta zuzen horretakoa ez den puntu bat ezagutzen badira.
Baita planoan dauden eta zuzen berekoak ez diren hiru puntu ezagutzen
badira ere. Azken bi kasu hauek erraz pasa daitezke lehenengo
kasukoak izatera ; beraz, puntu bat eta planoari buruz paraleloak
diren bi bektore jakinda ekuazio desberdinak lortzeko modua ikusiz
hasten da.
6.1. Bektore ekuazioa.
 puntutik igaro eta
puntutik igaro eta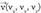 eta
eta bektoreei buruz paraleloaden planoa baldin Gadugu, plano horretako edozein X puntuk
bektoreei buruz paraleloaden planoa baldin Gadugu, plano horretako edozein X puntuk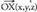 posizio bektorea izango du, eta bektore hori bi osagaietan deskonposa daiteke, bata jatorri puntutik planoko puntu batera doan
posizio bektorea izango du, eta bektore hori bi osagaietan deskonposa daiteke, bata jatorri puntutik planoko puntu batera doan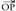 eta bestea P-tik X-era doan eta planoari buruz paraleloa den
eta bestea P-tik X-era doan eta planoari buruz paraleloa den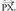 Beraz,
Beraz,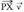 eta
eta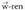 konposaketa lineal moduan idatz daiteke. Hortik ondorioz ateratzen da planoaren bektore ekuazioa, honako hau dela :
konposaketa lineal moduan idatz daiteke. Hortik ondorioz ateratzen da planoaren bektore ekuazioa, honako hau dela :
6.2. Parametro ekuazioak.
Aurreko bektore ekuaziotik ondorioztatzen dira, koordenatu bakoitzari dagozkion berdintzak esplizituki jarrita.
6.3. Ekuazio orokor edo inplizitua.
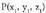 puntua planokoa izateko, bi parametro egon behar dute,
puntua planokoa izateko, bi parametro egon behar dute, eta
eta , eta horientzat parametro ekuazio hauek bete behar dira :
, eta horientzat parametro ekuazio hauek bete behar dira :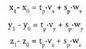 Horrek zera esan nahi du, alegia, hiru ekuazio eta bi ezezaguneko,
Horrek zera esan nahi du, alegia, hiru ekuazio eta bi ezezaguneko, eta
eta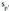 sistema gisa hartzen badugu, emaitzak izan behar dituela.
sistema gisa hartzen badugu, emaitzak izan behar dituela.
Planoa sortzen duten eta
eta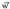 bektoreak linealki askeak direnez, koefizienteen matrizeak duen heina bi da. Sistema bateragarria eta zehatza izango da eta emaitza bat izango du, baldin eta matrizearen determinantea zero bada, izan ere, orduan, matrize zabalduaren heina ere bi izango baita. hau da :
bektoreak linealki askeak direnez, koefizienteen matrizeak duen heina bi da. Sistema bateragarria eta zehatza izango da eta emaitza bat izango du, baldin eta matrizearen determinantea zero bada, izan ere, orduan, matrize zabalduaren heina ere bi izango baita. hau da :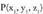 puntua ordea, planoko edozein puntu da ; beraz, zera idatz daiteke, alegia, (x,y,z) koordenatuak dituen planoko edozein punturentzat, determinantea zero izateko baldintza bete egin behar dela.
puntua ordea, planoko edozein puntu da ; beraz, zera idatz daiteke, alegia, (x,y,z) koordenatuak dituen planoko edozein punturentzat, determinantea zero izateko baldintza bete egin behar dela.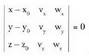 Determinantea garatuz, ondorengoa ateratzen da :
Determinantea garatuz, ondorengoa ateratzen da :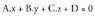 Planoaren ekuazio orokorra hain zuzen ere.Adibidea :1. Kalkula itzazu A(1,0, 1) puntutik igarotzen den eta
Planoaren ekuazio orokorra hain zuzen ere.Adibidea :1. Kalkula itzazu A(1,0, 1) puntutik igarotzen den eta eta
eta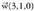 bektoreei buruz paraleloa den planoaren bektore ekuazioa, parametro ekuazioa eta ekuazio orokor edo inplizitua.Bektore ekuazioa zera da: (x, y z) = (1, 0, 1) + t(1, 0, 4) + s(3, 1, 0)Parametro ekuazioak honako hauek dira :
bektoreei buruz paraleloa den planoaren bektore ekuazioa, parametro ekuazioa eta ekuazio orokor edo inplizitua.Bektore ekuazioa zera da: (x, y z) = (1, 0, 1) + t(1, 0, 4) + s(3, 1, 0)Parametro ekuazioak honako hauek dira :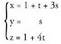 Ekuazio orokorra :
Ekuazio orokorra :
Kalkulatu planoaren ekuazioa beste datu batzuekin.
1. Hiru puntu emanda :Kalkulatu A(-2, 1, 2), B(1, -1, 0) eta C(0, 1, 1) puntuak barne
dituen planoaren ekuazioa.Lerrokatuta ez dauden hiru puntu emanik, horietako bi, edozein, elkartzen dituen bektorea planoan dago. Planoko puntutzat edozein puntu hartuta ere, A adibidez, eta halaber eta
eta bektoreak planoaren bektore paralelo moduan, berehala lortzen da bektore ekuazioa.Adibide honetan, AB = (1, -1, 0) - (-2, 1, 2) _ (3, -2, -2)Ac = (0, 1, 1) - (-2,1, 2) _ (2, 0, 1)Bektore ekuazioa ondorengoa da :(x, y, z) = (-2, 1, 2) + t(3, -2, -2) + s(2, 0, 1)Eta ekuazio orokorra:
bektoreak planoaren bektore paralelo moduan, berehala lortzen da bektore ekuazioa.Adibide honetan, AB = (1, -1, 0) - (-2, 1, 2) _ (3, -2, -2)Ac = (0, 1, 1) - (-2,1, 2) _ (2, 0, 1)Bektore ekuazioa ondorengoa da :(x, y, z) = (-2, 1, 2) + t(3, -2, -2) + s(2, 0, 1)Eta ekuazio orokorra: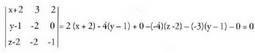 Sinplifikatuta :
Sinplifikatuta : 2. Planoaren ekuazioa planoko puntu bat eta zuzen bat jakinda.Kalkula itzazu A(O, 2, 2) puntua eta (x, y, z) = (1, -1, -1) + t(1, 0, 1)
zuzena dituen planoaren bektore ekuazioa eta ekuazio orokor edo
inplizitua.Emandako puntua, A kasu honetan, ezin daiteke zuzenekoa izan.Planoan A puntua ezaguna da eta baita hari buruz paraleloa den
bektorea ere, zuzenaren norabide bektorea hain zuzen. Beste bektore
bat falta da bektore ekuazioa ezarri ahal izateko. B(1, -1, -1) puntua,
zuzeneko puntua da ; beraz, A eta B elkartzen dituen bektoreak
planoan egon behar du.Gainera, A zuzenekoa ez denez, AB bektorea zuzenaren norabide
bektorearekiko askea da. Adibide honetan :AB = (1, -1, -1) - (o, 2, 2) = (1, -3, -3)Bektore ekuazioa : (x, y, z) = (0, 2, 2) + t(1, -3, -3) + s(1, 0, 1)Ekuazio orokorra :
2. Planoaren ekuazioa planoko puntu bat eta zuzen bat jakinda.Kalkula itzazu A(O, 2, 2) puntua eta (x, y, z) = (1, -1, -1) + t(1, 0, 1)
zuzena dituen planoaren bektore ekuazioa eta ekuazio orokor edo
inplizitua.Emandako puntua, A kasu honetan, ezin daiteke zuzenekoa izan.Planoan A puntua ezaguna da eta baita hari buruz paraleloa den
bektorea ere, zuzenaren norabide bektorea hain zuzen. Beste bektore
bat falta da bektore ekuazioa ezarri ahal izateko. B(1, -1, -1) puntua,
zuzeneko puntua da ; beraz, A eta B elkartzen dituen bektoreak
planoan egon behar du.Gainera, A zuzenekoa ez denez, AB bektorea zuzenaren norabide
bektorearekiko askea da. Adibide honetan :AB = (1, -1, -1) - (o, 2, 2) = (1, -3, -3)Bektore ekuazioa : (x, y, z) = (0, 2, 2) + t(1, -3, -3) + s(1, 0, 1)Ekuazio orokorra :
Hiru plano koordenatuen ekuazioak.
OX eta OY ardatzak barne dituen planoa, 0(0,0,0) jatorri puntutik igarotzen da eta OX ardatzaren arabera doan bektorearekiko nahiz OY ardatzaren arabera doan
bektorearekiko nahiz OY ardatzaren arabera doan bektoreari buruz paraleloa da. Beraz, bere bektore ekuazioa, honako hau izango da :
bektoreari buruz paraleloa da. Beraz, bere bektore ekuazioa, honako hau izango da :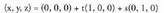 Bere ekuazio orokorra berriz, hau du :
Bere ekuazio orokorra berriz, hau du : Beraz, OY eta OZ barne dituen planoa, arrazoi berarengatik, hau
izango da :
Beraz, OY eta OZ barne dituen planoa, arrazoi berarengatik, hau
izango da :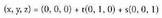 eta ekuazio orokorra x = 0 du.OX eta OZ barne dituen planoa berriz :
eta ekuazio orokorra x = 0 du.OX eta OZ barne dituen planoa berriz : eta bere ekuazio orokorra y = 0 du.
eta bere ekuazio orokorra y = 0 du.
- Ariketak
13. Kalkula itzazu A(1,1,1) puntutik igaro eta eta
eta
6.4. Puntu bat plano batekoa izateko baldintzak.
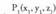 puntu bat era orokorrean emanik dagoen plano batekoa izan dadin, ekuazio orokorra bete behar du puntu horrek, hau da,
puntu bat era orokorrean emanik dagoen plano batekoa izan dadin, ekuazio orokorra bete behar du puntu horrek, hau da, ekuazioak egiazkoa izan behar du.Bektore eran edo parametro eran emana badago, bi balio egon behar dute,
ekuazioak egiazkoa izan behar du.Bektore eran edo parametro eran emana badago, bi balio egon behar dute, eta
eta , parametro ekuazioak eta bektore ekuazioa bete daitezen. Horrek, ondorengo determinantea zero izatea eskatzen du :
, parametro ekuazioak eta bektore ekuazioa bete daitezen. Horrek, ondorengo determinantea zero izatea eskatzen du :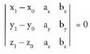 Adibideak :1. A(1, 1, -2) puntua, 2x + y + z -1 = 0 planokoa da eta ez da 2x -
y - z + 2 = 0 ekuaziodun planokoa, izan ere, lehenengo planoaren
ekuazioan ordezkatuta, hau gelditzen da :
Adibideak :1. A(1, 1, -2) puntua, 2x + y + z -1 = 0 planokoa da eta ez da 2x -
y - z + 2 = 0 ekuaziodun planokoa, izan ere, lehenengo planoaren
ekuazioan ordezkatuta, hau gelditzen da :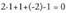 egia dena eta bigarrenean aldiz,
egia dena eta bigarrenean aldiz,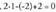 ez da egia, izan ere,
ez da egia, izan ere,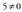 baita.2. Esan ea P(1,0,3) eta Q(0,1,3) puntuak p planokoak diren ; p
planoaren parametro ekuazioak ondorengoak dira :
baita.2. Esan ea P(1,0,3) eta Q(0,1,3) puntuak p planokoak diren ; p
planoaren parametro ekuazioak ondorengoak dira : Lehenengo bi ekuazioak batuz, 3s = 0 ateratzen da. Emaitzak beraz, s = 0 eta t = 2 dira. Hirugarren ekuazioan ordezkatzen badira, hark ere bete egiten du baldintza ; beraz,
Lehenengo bi ekuazioak batuz, 3s = 0 ateratzen da. Emaitzak beraz, s = 0 eta t = 2 dira. Hirugarren ekuazioan ordezkatzen badira, hark ere bete egiten du baldintza ; beraz,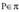 da.Era berean, Q-rentzat sistemak emaitzarik ba al duen ikusi behar
da :
da.Era berean, Q-rentzat sistemak emaitzarik ba al duen ikusi behar
da : Lehenengo bi ekuazioak ebatziz, t = 1 eta s = 0 ematen dute.
Lehenengo bi ekuazioak ebatziz, t = 1 eta s = 0 ematen dute.
Azken ekuazioan ordezkatuta, 2 = 1 gelditzen da eta hori ez da egia ; beraz,
6.5. Lau puntu planokideak edo plano berekoak izateko baldintza.
Lau puntu :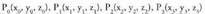 planokideak dira, balin eta horietako batek, heste hiruei definitutako planoaren ekuazioa betetzen badu, hau da :
planokideak dira, balin eta horietako batek, heste hiruei definitutako planoaren ekuazioa betetzen badu, hau da :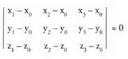 Beraz, ariketa, diferentzien determinantea kalkulatzera mugatzen
da.Ekuazio hori berbera lortzen da,
Beraz, ariketa, diferentzien determinantea kalkulatzera mugatzen
da.Ekuazio hori berbera lortzen da, puntua
puntua eta
eta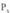 Puntuek definitutako planokoa izatea eskatu ordez,
Puntuek definitutako planokoa izatea eskatu ordez,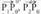 eta
eta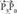 alde desberdinak lituzkeen paralelepipedoaren bolumena zero izateko baldintza jartzen bada. Hau da,
alde desberdinak lituzkeen paralelepipedoaren bolumena zero izateko baldintza jartzen bada. Hau da,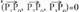 biderkadura mistoa zero izanda. Hiru bektore horien biderkadura mistoaren adierazpena, aurreko determinantea bera da.Adibideak:a) Planokideak al dira A(2,1,1), B(3,1,0), C(4,0,-1), D(5,-1,-2)
puntuak?
biderkadura mistoa zero izanda. Hiru bektore horien biderkadura mistoaren adierazpena, aurreko determinantea bera da.Adibideak:a) Planokideak al dira A(2,1,1), B(3,1,0), C(4,0,-1), D(5,-1,-2)
puntuak? AB, AC eta AD bektoreak elkarren mendekoak dira ; beraz, planokideak
dira lau puntuak.b) Planokideak al dira A(1,0,0), B(0,1,0), C(0,0,1), D(1,1,1)puntuak?
AB, AC eta AD bektoreak elkarren mendekoak dira ; beraz, planokideak
dira lau puntuak.b) Planokideak al dira A(1,0,0), B(0,1,0), C(0,0,1), D(1,1,1)puntuak?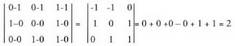
- Ariketak
16. Esan ea planokideak diren :
VII. Bi planoen posizio erlatiboa.
Geometria analitikoan bi planoen posizio erlatiboak aztertzeko,
beren bi ekuazioek batera eratzen duten bi ekuazio eta hiru ezezaguneko
sistemak dituen emaitzak eztabaidatzen dira :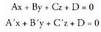 Koefizienteen matrizea honako hau da :
Koefizienteen matrizea honako hau da :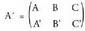 eta matrize zabaldua:
eta matrize zabaldua: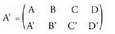 Aukera hauek dira:
Aukera hauek dira: , hau da,
, hau da,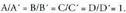 Bi planoak bat datoz, hots berbera dira.A heina = 1 eta
Bi planoak bat datoz, hots berbera dira.A heina = 1 eta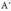 heina = 2, hau da,
heina = 2, hau da,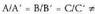 Ez dago puntu komunik planoen artean ; beraz, planoak paraleloak dira.A heina =
Ez dago puntu komunik planoen artean ; beraz, planoak paraleloak dira.A heina =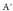 heina = 2. Orduan sistemak badu emaitza, baina ezezagunak hiru direnez, sistema bateragarria eta zehazgabea da.
heina = 2. Orduan sistemak badu emaitza, baina ezezagunak hiru direnez, sistema bateragarria eta zehazgabea da.
Emaitza parametro baten baitakoa da, zuzena da.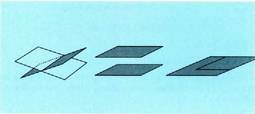 Adibidea:1. Azter ezazu plano hauen posizio erlatiboa.
Adibidea:1. Azter ezazu plano hauen posizio erlatiboa.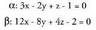 , denez, bi planoak paraleloak dira.2. Azter ezazu plano hauen posizio erlatiboa :
, denez, bi planoak paraleloak dira.2. Azter ezazu plano hauen posizio erlatiboa :
7. 1. Planoari buruz zuta den bektorea. Bi planoen ebakidura den zuzena.
Plano batek bere paralelo diren norabideen kopuru infinitua du,
izan ere, planoko puntuak, bi dimentsiotako bektore espazioarekin
harremanetan jar baitaitezke. Hala ere ordea, norabide bakarra dago
plano bati buruz zuta dena. Horregatik, plano baten bektore perpendikularra
ezagutzea, garrantzitsua da zehazteko garaian.Bedi Ax + By + Cz + D = 0 ekuaziodun p planoa. Planoari buruz
zuta den bektorea planoan dauden bektore guztiei buruz zuta izango
da.Bektore bat beste bati buruz zuta izan dadin eskatzea bi bektore horien biderkadura eskalarra zero izatea eskatzea da. planoari buruz zuta den bektorea bada, planoari buruz paraleloa den
planoari buruz zuta den bektorea bada, planoari buruz paraleloa den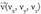 bektore ororekiko, hau beteko du:
bektore ororekiko, hau beteko du: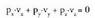 Planoari buruz paraleloa den bektore bat, planoko bi puntu elkartuz lortutako
Planoari buruz paraleloa den bektore bat, planoko bi puntu elkartuz lortutako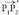 bektorearen ekipolentea da. Bitez
bektorearen ekipolentea da. Bitez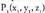 eta
eta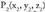 planoko bi puntu. Planoari buruz paraleloa den bektore bat
planoko bi puntu. Planoari buruz paraleloa den bektore bat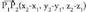 da. Bestalde, planoko puntuak izateagatik,
da. Bestalde, planoko puntuak izateagatik,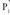 eta
eta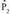 puntuen koordenatuek, planoaren ekuazioa bete egiten dute :
puntuen koordenatuek, planoaren ekuazioa bete egiten dute :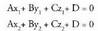 Eta kenketa eginez, hau ateratzen da :
Eta kenketa eginez, hau ateratzen da :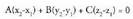 Baina hori, planoari buruz paralelga den bektore baten biderkadura eskalarraren adierazpena da,
Baina hori, planoari buruz paralelga den bektore baten biderkadura eskalarraren adierazpena da, - rena (A,B,C) koordenatuak dituen beste batekin eta biak elkarzutak dira,
- rena (A,B,C) koordenatuak dituen beste batekin eta biak elkarzutak dira, eta
eta puntuak zeintzuk diren kontuan hartu gabe.Beraz, ekuazioa
puntuak zeintzuk diren kontuan hartu gabe.Beraz, ekuazioa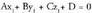 duen edozein planorentzat, (A,B,C) bektorea planoari buruz zuta da.Adibidea:1. Kalkulatu planoari buruz zuta den bektorea
duen edozein planorentzat, (A,B,C) bektorea planoari buruz zuta da.Adibidea:1. Kalkulatu planoari buruz zuta den bektorea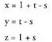 Era orokorrean jarrita, honako hau da planoaren ekuazioa :
Era orokorrean jarrita, honako hau da planoaren ekuazioa :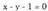 Plano horri buruz zuta bektore perpendikularra, (1,-1,0) da.
Plano horri buruz zuta bektore perpendikularra, (1,-1,0) da.
Planoa sortzen duten bektoreei buruz zuta dela egiazta daiteke.
Plano horren bektore ekuazioa, honako hau da :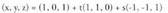 (1, -1, 0) bektorea, planoaren paraleloak diren (1, 1, 0) eta
(-1, -1, 1) bektoreen perpendikularra da.
(1, -1, 0) bektorea, planoaren paraleloak diren (1, 1, 0) eta
(-1, -1, 1) bektoreen perpendikularra da.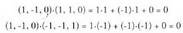 2. Kalkulatu z = 0 planoaren bektore perpendikular bat.z = 0 planoa, plano koordenatu horizontala da. Bektore perpendikular bat (0,0,1) da, oinarri cartesiar edo ortonormaleko
2. Kalkulatu z = 0 planoaren bektore perpendikular bat.z = 0 planoa, plano koordenatu horizontala da. Bektore perpendikular bat (0,0,1) da, oinarri cartesiar edo ortonormaleko bektorea.Paraleloak ez diren bi planok, zuzena zehazten dute :
bektorea.Paraleloak ez diren bi planok, zuzena zehazten dute :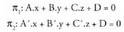 Zuzen horren bektore ekuazioa, parametro ekuazioa edota ekuazio
jarraia ezagutzeko, sistemaren emaitzak, parametroren baten
baitan lor daitezke edota puntu bat eta zuzenaren norabide bektoreren
bat kalkula daitezke.Zuzenaren parametro ekuazioak diren emaitzak ezagutzeko, bi
planoen ekuazioek eratzen dituzten bi ekuazio eta hiru ezezaguneko
sistema ebazten da, sistema bateragarri zehazgabeentzako ohiko
metodoak erabiliz. Gai askeak, zuzenean puntu batek dituen koordenatuak
izango dira eta x,y,z ezezagunen parametroaren koefizienteak,zuzenaren
norabide bektorearen osagaiak izango dira.Adibidea :Kalkula ezazu plano hauek definitutako zuzenaren bektore ekuazioa
:
Zuzen horren bektore ekuazioa, parametro ekuazioa edota ekuazio
jarraia ezagutzeko, sistemaren emaitzak, parametroren baten
baitan lor daitezke edota puntu bat eta zuzenaren norabide bektoreren
bat kalkula daitezke.Zuzenaren parametro ekuazioak diren emaitzak ezagutzeko, bi
planoen ekuazioek eratzen dituzten bi ekuazio eta hiru ezezaguneko
sistema ebazten da, sistema bateragarri zehazgabeentzako ohiko
metodoak erabiliz. Gai askeak, zuzenean puntu batek dituen koordenatuak
izango dira eta x,y,z ezezagunen parametroaren koefizienteak,zuzenaren
norabide bektorearen osagaiak izango dira.Adibidea :Kalkula ezazu plano hauek definitutako zuzenaren bektore ekuazioa
: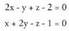 x = t eginda,
x = t eginda,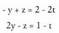 Batuta, y = 3 - 3t gelditzen da ; ordezkatu eta askatu ondoren :z=5-5tBeraz, honako hau izango da zuzena :
Batuta, y = 3 - 3t gelditzen da ; ordezkatu eta askatu ondoren :z=5-5tBeraz, honako hau izango da zuzena :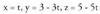 (0,3,5) puntutik igaro eta (1,-3,-5) norabide bektorea duen zuzena
alegia.Hori egiteko beste modu bat zera da, norabide bektorea eta zuzenaren
puntu bat kalkulatzetik abiatzea. Puntu solteren bat jakin
nahi bada, ezezagun bati balioak eman eta sistema beste bientzat
ebazten da. Gelditzen den sistema bateragarri eta zehatza ez bada,
beste ezezagun desberdinari balio desberdinen bat ematen zaio.Norabide bektorea kalkulatzeko, (A,B,C) bektorea plano bati eta
(0,3,5) puntutik igaro eta (1,-3,-5) norabide bektorea duen zuzena
alegia.Hori egiteko beste modu bat zera da, norabide bektorea eta zuzenaren
puntu bat kalkulatzetik abiatzea. Puntu solteren bat jakin
nahi bada, ezezagun bati balioak eman eta sistema beste bientzat
ebazten da. Gelditzen den sistema bateragarri eta zehatza ez bada,
beste ezezagun desberdinari balio desberdinen bat ematen zaio.Norabide bektorea kalkulatzeko, (A,B,C) bektorea plano bati eta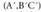 besteari buruz zutak direlakotik abiatzen da. Zuzenaren norabidea, bi planoekiko norabide komuna den bakarra, bi bektore horiei buruz zuta izango da. Baina bi bektoreren biderkadura bektorialabiei buruz zuta da ; beraz, norabide bektorea bi bektore horien biderkadura bektoriala da :
besteari buruz zutak direlakotik abiatzen da. Zuzenaren norabidea, bi planoekiko norabide komuna den bakarra, bi bektore horiei buruz zuta izango da. Baina bi bektoreren biderkadura bektorialabiei buruz zuta da ; beraz, norabide bektorea bi bektore horien biderkadura bektoriala da :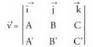 Adibidea :Bi plano hauek :
Adibidea :Bi plano hauek :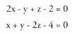 zuzena zehazten dute. Kalkula ezazu bere bektore ekuazioa.z-ri 0 balioa emanez, x = 2 eta y = 2 lortzen dira. Bi planoetakoa
den puntu bat, (2,2,0) da.Norabide bektorea kalkulatzeko :
zuzena zehazten dute. Kalkula ezazu bere bektore ekuazioa.z-ri 0 balioa emanez, x = 2 eta y = 2 lortzen dira. Bi planoetakoa
den puntu bat, (2,2,0) da.Norabide bektorea kalkulatzeko :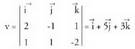 Beraz, zuzenaren bektore ekuazioa, honako hau da :
Beraz, zuzenaren bektore ekuazioa, honako hau da :
7.2. Ariketak.
1. Kalkula ezazu puntu bat bere barne duen eta emandako beste
plano baten paraleloa den planoa. Adibidez : Kalkula ezazu (1,1,0)
puntutik pasaz 2x - y - z + 4 = 0 ekuazioa duen planoaren paraleloa
den planoaren ekuazioa.Bi plano paralelok A,B,C koefizienteak proportzionalak dituzte,
edota bestela esan nahi bada, (A,B,C) bektore berberari buruz zutak
dira. Hau da, emandako planoari buruz paraleloa denez, eskatutako
planoa era honetakoa izango da :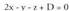 (1,1,0) puntutik igarotzen denez, hau bete behar du :
(1,1,0) puntutik igarotzen denez, hau bete behar du : Beraz, D = -1.Emaitza : 2x - y - z - 1 = 0Orokorki, Ax + By + Cz + D = 0 planoari buruz paraleloa den eta
Beraz, D = -1.Emaitza : 2x - y - z - 1 = 0Orokorki, Ax + By + Cz + D = 0 planoari buruz paraleloa den eta puntutik igarotzen den planoa honako hau da :
puntutik igarotzen den planoa honako hau da :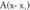 2. Kalkulatu puntu batetik igaroz zuzen bati buruz zuta den planoaren
ekuazioa. Adibidez, kalkulatu P(1,0,1) puntutik igaroz,
(x,y,z) = (0,0, 1) + t(1,-1,2) zuzenari buruz zuta den planoaren ekuazioa
.(1,-1,2) bektorea, planoari buruz zuta da ; beraz, planoaren ekuazio
orokorra, honako hau izango da :
2. Kalkulatu puntu batetik igaroz zuzen bati buruz zuta den planoaren
ekuazioa. Adibidez, kalkulatu P(1,0,1) puntutik igaroz,
(x,y,z) = (0,0, 1) + t(1,-1,2) zuzenari buruz zuta den planoaren ekuazioa
.(1,-1,2) bektorea, planoari buruz zuta da ; beraz, planoaren ekuazio
orokorra, honako hau izango da :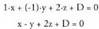 P(1,0,1) puntutik igarotzen denez, hau bete behar du : Sinplifikatuta : -x + 4y - 2z + 5 = 0
P(1,0,1) puntutik igarotzen denez, hau bete behar du : Sinplifikatuta : -x + 4y - 2z + 5 = 0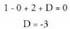 Beraz, ekuazioa x - y + 2z - 3 = 0 da.3. Kalkulatu elkar ebakitzen
planoaren ekuazioa.
Beraz, ekuazioa x - y + 2z - 3 = 0 da.3. Kalkulatu elkar ebakitzen
planoaren ekuazioa.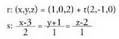 r zuzena R(1,0,2) puntutik igarotzen da eta
r zuzena R(1,0,2) puntutik igarotzen da eta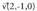 norabide bektorea du. s zuzena berriz, S(3,-1,2) puntutik igaro tz en da eta
norabide bektorea du. s zuzena berriz, S(3,-1,2) puntutik igaro tz en da eta norabide bektorea du. Froga daiteke noski,
norabide bektorea du. Froga daiteke noski, eta
eta bektoreen errenkaden determinantea eginda, bi zuzen horiek ebakitzaileak direla. Beraz, bene-benetan, horiek barne dituen planoa definitzen dute. Plano horren ekuazioa zehazteko, nahikoa da puntu baten koordenatuak eta plano horri buruz zuta den bektorea ezagutzea. r eta s zuzenetako puntu guztiak planokoak dira ; har dezagun R(1,0,2). Planoari buruz bektore zuta
bektoreen errenkaden determinantea eginda, bi zuzen horiek ebakitzaileak direla. Beraz, bene-benetan, horiek barne dituen planoa definitzen dute. Plano horren ekuazioa zehazteko, nahikoa da puntu baten koordenatuak eta plano horri buruz zuta den bektorea ezagutzea. r eta s zuzenetako puntu guztiak planokoak dira ; har dezagun R(1,0,2). Planoari buruz bektore zuta eta
eta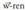 arteko biderkadura bektoriala da, izan ere, biderkadura bektorial hori planoan dauden bi bektoreei buruz zuta baita.
arteko biderkadura bektoriala da, izan ere, biderkadura bektorial hori planoan dauden bi bektoreei buruz zuta baita. Beraz, bektore perpendikular bat,
Beraz, bektore perpendikular bat, da eta planoaren ekuazioa:
da eta planoaren ekuazioa: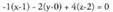 Sinplifikatuta :
Sinplifikatuta :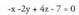 4. Kalkulatu bi zuzen paralelo barne dituen planoaren ekuazioa.
4. Kalkulatu bi zuzen paralelo barne dituen planoaren ekuazioa.
Bitez adibidez honako zuzen hauek : bere barne dituen planoaren ekuazioa kalkulatu behar da.Bi zuzenak zorrozki paraleloak dira, izan ere,
bere barne dituen planoaren ekuazioa kalkulatu behar da.Bi zuzenak zorrozki paraleloak dira, izan ere,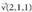 norabide bektorea berbera baita eta R(1,0,2) puntua eta S(1,-1,0) puntua elkartzen dituen
norabide bektorea berbera baita eta R(1,0,2) puntua eta S(1,-1,0) puntua elkartzen dituen bektorea, ez da
bektorea, ez da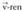 proportzionala ; beraz, biak ez datoz bat eta bi zuzen paralelo dira.Horiek barne dituen planoaren ekuazioa, puntu bat eta bektore perpendikular bat jakin beharra dago. r eta s zuzenen puntu guztiak, planoan daude. Ekuaziorako bat, edozein, hartzen da S(1,-1,0) adibidez. Planoari buruz zuta den bektore perpendikularrak, v(2,1,1) bektoreari buruz zuta izan behar du eta baita R eta S elkartzen dituen
proportzionala ; beraz, biak ez datoz bat eta bi zuzen paralelo dira.Horiek barne dituen planoaren ekuazioa, puntu bat eta bektore perpendikular bat jakin beharra dago. r eta s zuzenen puntu guztiak, planoan daude. Ekuaziorako bat, edozein, hartzen da S(1,-1,0) adibidez. Planoari buruz zuta den bektore perpendikularrak, v(2,1,1) bektoreari buruz zuta izan behar du eta baita R eta S elkartzen dituen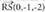 bektorearekiko ere bai. Planoari buruz bektore perpendikularra beren biderkadura bektoriala da :
bektorearekiko ere bai. Planoari buruz bektore perpendikularra beren biderkadura bektoriala da :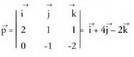 Bektore perpendikularra
Bektore perpendikularra da, eta planoaren ekuazioa :
da, eta planoaren ekuazioa :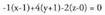 Simplifikatua:
Simplifikatua: 5. Kalkulatu zuzen bat barne duen eta beste plano bati buruz zuta
den planoaren ekuazioa.Bedi r : (x,y,z) = (1,0,1) + t(-1,1,0) zuzena eta P : x+y+z-3=0 plano
perpendikularra. r zuzena ezin daiteke plano horri buruz zuta izan,
zeren emaitza kopuru infinitua izango bailitzateke besela.Adibide honetan, paraleloa da.r zuzena barne duen plano batek, honako ekuazio hau du :
5. Kalkulatu zuzen bat barne duen eta beste plano bati buruz zuta
den planoaren ekuazioa.Bedi r : (x,y,z) = (1,0,1) + t(-1,1,0) zuzena eta P : x+y+z-3=0 plano
perpendikularra. r zuzena ezin daiteke plano horri buruz zuta izan,
zeren emaitza kopuru infinitua izango bailitzateke besela.Adibide honetan, paraleloa da.r zuzena barne duen plano batek, honako ekuazio hau du :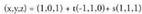 Itxura orokorrera pasaz :
Itxura orokorrera pasaz :
- Ariketak
17. Aurki ezazu honako plano hauen posizio erlatiboa : 18. Kalkula ezazu jatorri puntutik igaroz 3x - 4y + 2z - 7 =
0 planoaren paraleloa den planoaren ekuazioa.19. Kalkulatu ondoko bi plano hauek definitzen duten
zuzenaren bektore ekuazioa :
18. Kalkula ezazu jatorri puntutik igaroz 3x - 4y + 2z - 7 =
0 planoaren paraleloa den planoaren ekuazioa.19. Kalkulatu ondoko bi plano hauek definitzen duten
zuzenaren bektore ekuazioa :
VIII. Planoen eta zuzenen arteko posizio erlatiboa.
Plano bat eta zuzen bat, paraleloak izan daitezke edota elkar ebaki
dezakete, edota zuzena planoan kokatuta egon daiteke. Zuzenaren v norabide bektorea eta planoaren paraleloak diren w
eta u bektoreak ezagunak badira, beren posizio erlatiboa ezagutu
daiteke beren mendekotasun lineala aztertuta :a)
Zuzenaren v norabide bektorea eta planoaren paraleloak diren w
eta u bektoreak ezagunak badira, beren posizio erlatiboa ezagutu
daiteke beren mendekotasun lineala aztertuta :a) eta
eta konbinazio lineala ez bada, zuzenak planoa ebaki egiten du.b)
konbinazio lineala ez bada, zuzenak planoa ebaki egiten du.b) konbinazio lineala baldin bada, zuzeneko edozein puntu planokoa den egiaztatzen da.i) Planokoa bada, zuzena planokoa da.ii) Planokoa ez bada, zuzena eta planoa paraleloak dira.Planoa P : Ax + By + Cz + D = 0 era orokorrean emanik baldin badago eta zuzenaren
konbinazio lineala baldin bada, zuzeneko edozein puntu planokoa den egiaztatzen da.i) Planokoa bada, zuzena planokoa da.ii) Planokoa ez bada, zuzena eta planoa paraleloak dira.Planoa P : Ax + By + Cz + D = 0 era orokorrean emanik baldin badago eta zuzenaren norabide bektorea ezagutzen bada,
norabide bektorea ezagutzen bada, eta planoaren perpendikularra den (A,B,C) bektorea hartzen dira :a) Perpendikularrak ez badira, zuzena eta planoa ebakitzaileak
dira.b) Perpendikularrak badira :i) Zuzeneko edozein puntu planokoa bada, zuzena planokoa da.ii) Zuzeneko edozein puntu planokoa ez bada, zuzena eta planoa
paraleloak dira.Zuzena bi planoren ebakidura moduan emanda baldin badago,
ariketa, hiru ezezaguneko hiru ekuaziodun sistemaren ebazpen
bihurtzen da :
eta planoaren perpendikularra den (A,B,C) bektorea hartzen dira :a) Perpendikularrak ez badira, zuzena eta planoa ebakitzaileak
dira.b) Perpendikularrak badira :i) Zuzeneko edozein puntu planokoa bada, zuzena planokoa da.ii) Zuzeneko edozein puntu planokoa ez bada, zuzena eta planoa
paraleloak dira.Zuzena bi planoren ebakidura moduan emanda baldin badago,
ariketa, hiru ezezaguneko hiru ekuaziodun sistemaren ebazpen
bihurtzen da :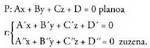 Koefizienteen matrizearen heina, gutxienez ere bi da, zeren, elkar
ebakiz zuzena ematen duten bi planoek ezin ditzakete eduki x,y,z
ezezagunen koefiziente proportzionalak. Hala izanez gero, bi plano
paralelo edo bat datozenak izango lirateke, eta hartara ez lukete
zuzena definituko.Koefizienteen matrizeak duen heina hiru bada, emaitza bakarra
izango da. Puntu batean ebakitzen dute elkar. Zuzena planoari
buruz paraleloa da.Matrize zabalduaren heina bi bada, zuzena planokoa da.Adibidea:1. Aurki ezazu ondorengo zuzenaren eta planoaren posizio erlatiboa
.
Koefizienteen matrizearen heina, gutxienez ere bi da, zeren, elkar
ebakiz zuzena ematen duten bi planoek ezin ditzakete eduki x,y,z
ezezagunen koefiziente proportzionalak. Hala izanez gero, bi plano
paralelo edo bat datozenak izango lirateke, eta hartara ez lukete
zuzena definituko.Koefizienteen matrizeak duen heina hiru bada, emaitza bakarra
izango da. Puntu batean ebakitzen dute elkar. Zuzena planoari
buruz paraleloa da.Matrize zabalduaren heina bi bada, zuzena planokoa da.Adibidea:1. Aurki ezazu ondorengo zuzenaren eta planoaren posizio erlatiboa
.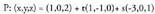 planoa eta
planoa eta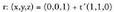 Ondoko determinantea kalkulatzen da :
Ondoko determinantea kalkulatzen da :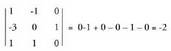 Beraz, zuzenaren bektorea ez dago planoari buruz paralelo direnen
artean eta zuzenak eta planoak elkar ebakitzen dute.2. Azter ezazu r :(x+2)/2 = (y-1)/1 = (z-3)/2 zuzenaren eta 2x-2yz-1=O
planoaren arteko posizio erlatiboa.Zuzenaren norabide bektorea (2,1,2) da eta planoari buruz zuta dena (2,-2,-1) da. Beren biderkadura eskalarra ondorengoa da :
Beraz, zuzenaren bektorea ez dago planoari buruz paralelo direnen
artean eta zuzenak eta planoak elkar ebakitzen dute.2. Azter ezazu r :(x+2)/2 = (y-1)/1 = (z-3)/2 zuzenaren eta 2x-2yz-1=O
planoaren arteko posizio erlatiboa.Zuzenaren norabide bektorea (2,1,2) da eta planoari buruz zuta dena (2,-2,-1) da. Beren biderkadura eskalarra ondorengoa da :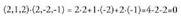 Beraz, zuzenaren norabidea planoari buruz paraleloa da. Zuzena
planoari buruz paraleloa den ala planokoa den jakiteko, P(-2,1,3)
puntua hartuko dugu, zuzen horretakoa dena eta horren koordenatuak
planoaren ekuazioan ordezkatuko ditugu :
Beraz, zuzenaren norabidea planoari buruz paraleloa da. Zuzena
planoari buruz paraleloa den ala planokoa den jakiteko, P(-2,1,3)
puntua hartuko dugu, zuzen horretakoa dena eta horren koordenatuak
planoaren ekuazioan ordezkatuko ditugu :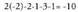 Beraz, zuzenekoa den puntu hori ez da planokoa eta zuzena planoaren
paraleloa da.3. Azter ezazu planoaren eta zuzenaren posizio erlatiboa :
Beraz, zuzenekoa den puntu hori ez da planokoa eta zuzena planoaren
paraleloa da.3. Azter ezazu planoaren eta zuzenaren posizio erlatiboa :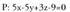 planoarenaeta ondoko bi plano hauen ebakidura moduan emandako zuzenarena
:
planoarenaeta ondoko bi plano hauen ebakidura moduan emandako zuzenarena
: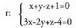 Honako sistema honek :
Honako sistema honek :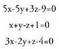 koefizienteen matrizea 2ko heina duena dauka :
koefizienteen matrizea 2ko heina duena dauka :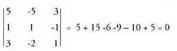 Matrize zabalduak zutabe bat gehiago du. Horren heina jakiteko,
x eta y-ren koefizienteak linealki askeak direla ikusten da eta pentsa
daiteke z-ren koefizienteen zutabea dela beste bien baitakoa edo
mendekoa dena. z-ren koefizienteen zutabea gai askeen zutabeaz
ordezkatzen bada, matrize zabalduaren heina 3 izango da matrize
horren determinantea zero ez bada. Zero bada berriz, gai askeak ere
x eta y-ren koefizienteen mendekoak dira :
Matrize zabalduak zutabe bat gehiago du. Horren heina jakiteko,
x eta y-ren koefizienteak linealki askeak direla ikusten da eta pentsa
daiteke z-ren koefizienteen zutabea dela beste bien baitakoa edo
mendekoa dena. z-ren koefizienteen zutabea gai askeen zutabeaz
ordezkatzen bada, matrize zabalduaren heina 3 izango da matrize
horren determinantea zero ez bada. Zero bada berriz, gai askeak ere
x eta y-ren koefizienteen mendekoak dira :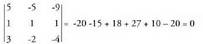 Beraz, matrize zabalduaren heina ere bi da. Zuzena planokoa da.
Beraz, matrize zabalduaren heina ere bi da. Zuzena planokoa da.
Heinen kalkulua ere ekidin daiteke, sistema Gaussen metodoaren
bitartez ebatziz, hau da, zenbakiz biderkatutako ekuazioak trukatuz,
batuz edo kenduz ezezagunen koefizienteak hutsalduz. Kasu
horretan, sistema honela idazten da :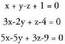 Lehenengo ekuazioa ken bi aldiz bigarrena egiten badugu eta
emaitza hirugarrenetik kentzen bada, ondoko hau lortzen da :
Lehenengo ekuazioa ken bi aldiz bigarrena egiten badugu eta
emaitza hirugarrenetik kentzen bada, ondoko hau lortzen da :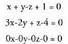
- Ariketak
20. Aurkitu honako hauen arteko posizio erlatiboa :a) x+y+z-3=0 planoaren eta (x,y,z) = (1,1,0) + t(1,-2,1) zuzenarena.b) 2x-y+z-3=0 planoaren eta x+y-z-1=0 eta x-y+z=O planoen ebakidura den zuzenarena.
IX. Bi zuzenen arteko angelua, zuzenaren eta planoaren artekoa eta bi planoen artekoa.
Prozedura beti ere, parte hartu behar duten zuzenen edo planoen norabideak emango dituzten bektore bikoteak aurkitzea da eta gero bektore horiek beren artean eratzen dituzten angeluak biderkadura eskalarraren bitartez aurkitzea, lortutako kosinuari dagokion arkua edo angelua ateraz. Bektoreak eta
eta badira :
badira :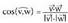
9. 1. Bi zuzenen arteko angelua.
P puntuan elkar ebakitzen duten r eta s zuzenak baditugu, bi
zuzen horiek beren artean eratzen dituzten bi angeluetako bat,
beren norabide bektoreek eratzen dutenaren berdina da. Bestea,
angelu horren betegarria da. Angelu hori kalkulatzeko, biderkadura
eskalarra erabiltzen da eta biderkadura horren formulak angelu
horren kosinua ematen du.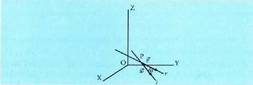 Adibidea :Kalkulatu bi zuzen hauek elkarren artean eratzen duten angelua :
Adibidea :Kalkulatu bi zuzen hauek elkarren artean eratzen duten angelua :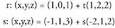 Bedi a angelu hori :
Bedi a angelu hori :
9.2. Bi planoek elkarren artean eratzen duten angelua.
Bi planoek elkarren artean eratzen duten angelua, plano horiei
buruz zutak diren bektoreek elkarren artean eratzen dutenaren
edota angelu horren betegarriaren berdina da. Bi planok elkar ebakitzean
lau angelu diedro eratzen dituzte eta bizbitara berdinak dira ;
beraz, bata perpendikularrek elkarren artean eratzen duten angeluaren
berdina izango da eta beste horren betegarria. Adibidea:Kalkula ezazu ondoko bi planook elkarren artean eratzen duten
angeluaren balioa.
Adibidea:Kalkula ezazu ondoko bi planook elkarren artean eratzen duten
angeluaren balioa. Bektore perpendikularrak honako hauek dira : (3,0,-4) eta (1,2-2).
Bektore perpendikularrak honako hauek dira : (3,0,-4) eta (1,2-2).
Eratzen duten angeluari deituta :
deituta :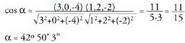
9.3. Zuzenaren eta angeluaren arteko angelua.
Zuzenak eta planoak elkarren artean eratzen duten angelua zuzenaren
norabide bektoreak eta planoaren bektore perpendikularrak
eratzen dutenaren angelu osagarria da. Kasu honetan ere angelu bat
edota bere betegarria kalkula daiteke, bektoreen noranzkoaren arabera
. Zuzenaren eta planoaren arteko angelutzat, 90° baino txikiagoa
den angelua hartzen da.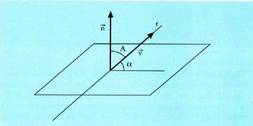 Adibidea:Kalkula ezazu r : (x,y,z) = (1,O,1) + t(1,O,1) zuzenak eta P : x-y+z-2=0
planoak eratzen duten angelua.Zuzenaren norabide bektorea, (1,0,1) da ; planoaren zuzen perpendikularrarena
berriz p(l,-1,1). Eratzen duten A angeluaren
kosinua berriz :
Adibidea:Kalkula ezazu r : (x,y,z) = (1,O,1) + t(1,O,1) zuzenak eta P : x-y+z-2=0
planoak eratzen duten angelua.Zuzenaren norabide bektorea, (1,0,1) da ; planoaren zuzen perpendikularrarena
berriz p(l,-1,1). Eratzen duten A angeluaren
kosinua berriz :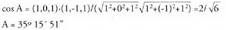 Beraz, planoaren eta zuzenaren arteko angelua, honako hau izango
da :
Beraz, planoaren eta zuzenaren arteko angelua, honako hau izango
da :
9.4. Paralelotasuna eta perpendikulartasuna.
Puntu jakin batetik igaro eta beste plano bati buruz paraleloa den planoaren ekuazioa jakin nahi baldin bada, emaitza bakarra da.
Emandako planoa bada
bada puntutik pasa behar badu, P-tik igaro eta
puntutik pasa behar badu, P-tik igaro eta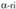 buruz paraleloa den planoaren ekuazioa, honako hau izango da :
buruz paraleloa den planoaren ekuazioa, honako hau izango da :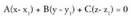 Era berean,
Era berean,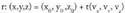 zuzenari buruz paraleloa izan eta
zuzenari buruz paraleloa izan eta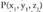 puntutik igarotzen dena, erraz kalkula daiteke. Horretarako nahikoa da zuzenaren ekuazioaren puntua aldatzea.Zuzen paraleloaren ekuazioa honako hau da :
puntutik igarotzen dena, erraz kalkula daiteke. Horretarako nahikoa da zuzenaren ekuazioaren puntua aldatzea.Zuzen paraleloaren ekuazioa honako hau da :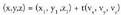 Baina, Ax + By + Cz + D = 0 planoaren paraleloa izan eta puntu jakin batetik igarotzen den zuzena aurkitu nahi bada, emaitza kopuru infinitua izango da. Planoaren perpendikularra den bektorea (A,B,C) da eta puntutik igaroz bektore perpendikular horrekiko norabide bektore perpendikularra duten zuzen guztiak planoari buruz paraleloak dira. (-B,A,O) edo (O,-C,B) edo (-C,O,A) bektoreak (A,B,C) bektoreari buruz zutak dira. Hiru bektore horietatik bi bederen hutsalak ez direla baiezta daiteke. Bitez (-B,A,O) eta (0,- C,B) hutsalak ez direnak; horretara,
Baina, Ax + By + Cz + D = 0 planoaren paraleloa izan eta puntu jakin batetik igarotzen den zuzena aurkitu nahi bada, emaitza kopuru infinitua izango da. Planoaren perpendikularra den bektorea (A,B,C) da eta puntutik igaroz bektore perpendikular horrekiko norabide bektore perpendikularra duten zuzen guztiak planoari buruz paraleloak dira. (-B,A,O) edo (O,-C,B) edo (-C,O,A) bektoreak (A,B,C) bektoreari buruz zutak dira. Hiru bektore horietatik bi bederen hutsalak ez direla baiezta daiteke. Bitez (-B,A,O) eta (0,- C,B) hutsalak ez direnak; horretara,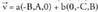 a eta b errealak eta aldi berean zero ez direnak dituztenak, planoari buruz paraleloak dira. Beraz, zuzen ugari (infinitu) daude baldintza hauek betetzen dituztenak.
a eta b errealak eta aldi berean zero ez direnak dituztenak, planoari buruz paraleloak dira. Beraz, zuzen ugari (infinitu) daude baldintza hauek betetzen dituztenak.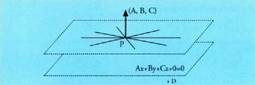 Era berean, puntu batetik pasa eta beste plano bati buruz zutak diren planoen ekuazioak kalkulatu nahi baldin baditugu, emaitzak infinituak dira, ezen, Ax + By + Cz + D = 0 planoa emanik,
Era berean, puntu batetik pasa eta beste plano bati buruz zutak diren planoen ekuazioak kalkulatu nahi baldin baditugu, emaitzak infinituak dira, ezen, Ax + By + Cz + D = 0 planoa emanik,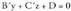 ekuaziodun planoak, beren koefizienteek a eta b errealak direla
ekuaziodun planoak, beren koefizienteek a eta b errealak direla betetzen dutenak eta aldi berean zero ez direnak, eman den planoari buruz zutak dira.Hain zuzen ere, horrela ateratako
betetzen dutenak eta aldi berean zero ez direnak, eman den planoari buruz zutak dira.Hain zuzen ere, horrela ateratako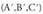 bektorea, (A,B,C) bektoreari buruz zuta delako.
bektorea, (A,B,C) bektoreari buruz zuta delako.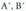 eta
eta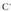 koefizienteak jakin ondoren,
koefizienteak jakin ondoren, balioa, planoa emandako puntutik igarotzeko moduan finkatzen da.
balioa, planoa emandako puntutik igarotzeko moduan finkatzen da. Era berean, zehazgabea da puntu batetik pasaz zuzen bati buruz
paraleloa den ekuazioa kalkulatzeko ariketa, izan ere, planoa definitzeko,
puntuaz gainera, bi norabide desberdin ere behar baitira.
Era berean, zehazgabea da puntu batetik pasaz zuzen bati buruz
paraleloa den ekuazioa kalkulatzeko ariketa, izan ere, planoa definitzeko,
puntuaz gainera, bi norabide desberdin ere behar baitira.
Bestalde, ongi definituta dago zuzen bati buruz zuta izanik emandako
puntu jakin batetik igarotzen den zuzenaren ekuazioa kalkulatzeko
ariketa. Horretarako, puntu horretatik igarotzen den zuzenari
buruz zuta den planoa kalkulatzen da. Plano horrek zuzena
ebakitzen duen puntua, aurkitu nahi den zuzenaren beste puntu bat
da eta horrekin jada badira bi puntu zuzena definitzeko.Adibideak:1. Kalkula ezazu P(O,-2,2) puntutik igaroz r: (x-1)/2 = (y+l)/1 = _ (z+1)/(-1) zuzenari buruz zuta den zuzenaren ekuazioa.. -ren norabide bektorea da,eta P-tik igarotzen den r-ren plano perpendikularra : 2x+1(y+2)-
1(z-2) = 0 da.Plano horren eta r-ren arteko ebaki puntua kalkulatzeko, r, parametro
ekuazioen bidez adieraziko dugu :
da,eta P-tik igarotzen den r-ren plano perpendikularra : 2x+1(y+2)-
1(z-2) = 0 da.Plano horren eta r-ren arteko ebaki puntua kalkulatzeko, r, parametro
ekuazioen bidez adieraziko dugu :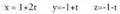 eta planoaren ekuazioan ordezkatzen da:
eta planoaren ekuazioan ordezkatzen da: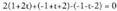 6t+6 = 0, eta hortik, t = -1Beraz, ebaki puntua : S(-1,-2,0) da.
6t+6 = 0, eta hortik, t = -1Beraz, ebaki puntua : S(-1,-2,0) da.
(0,-2,2) puntutik pasaz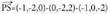 norabide bektoretzat duen zuzena da ; beraz, bere ekuazioa, honako hau izango du :
norabide bektoretzat duen zuzena da ; beraz, bere ekuazioa, honako hau izango du :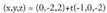 2. Aurkitu x-z+2 = 0 eta x-y-z-3 = 0 planoen plano zuta, jatorritik
igaro behar duela kontuan harturik.Bi planoei buruz zuta den planoa plano biek elkar ebakitzean definitzen duten zuzenaren zuta da, eta haren ekuazio aljebraikoa ezaguna da haren puntu bat, O (0,0,0), eta bi bektore, bi planoen zutak, ezagutzen direlako. Beraz, ekuazio bektorial hau du :
2. Aurkitu x-z+2 = 0 eta x-y-z-3 = 0 planoen plano zuta, jatorritik
igaro behar duela kontuan harturik.Bi planoei buruz zuta den planoa plano biek elkar ebakitzean definitzen duten zuzenaren zuta da, eta haren ekuazio aljebraikoa ezaguna da haren puntu bat, O (0,0,0), eta bi bektore, bi planoen zutak, ezagutzen direlako. Beraz, ekuazio bektorial hau du :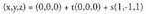
- Ariketak
2 1. Kalkula ezazu ondoko planoek eratzen duten angelua :a) x-y+z+4=0 planoak eta 2x-y-3z+2=0 planoak.b) x+y+z-1=O planoak eta x=0 planoak.22. Kalkula ezazu (x,y,z) = (0,0,0) + t(1,0,-1) zuzenak eta 2x-y-z+3=0 planoak eratzen duten angelua.23. Kalkula ezazu r : (x,y,z) = (1,1,1)+ t(1,2,-1) eta s : (x,y,z) = (3,1,3)+ t(1,0,1) zuzenek eratzen duten angelua.24. Kalkula ezazu x-3y-2z-4=0 planoaren perpendikularra izan eta P(1,1,-2) puntutik igarotzen den zuzenaren ekuazioa .25. Kalkula ezazu (x-1)/2 = (y+l)/2 = (z-2)/3 zuzenaren perpendikularra izanik P(1,1,0) puntutik igarotzen den planoaren ekuazioa.
X. Puntuen, zuzenen eta planoen arteko distantziak. Tetraedroaren bolumena.
Bi puntuen arteko distantzia.
 eta
eta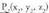 puntuak emanik, bi puntu horien arten distantzia,
puntuak emanik, bi puntu horien arten distantzia,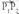 , bektorearen modulua da. Oinarria ortonormala duenez, bektore horrek honako balio hau izango du :
, bektorearen modulua da. Oinarria ortonormala duenez, bektore horrek honako balio hau izango du :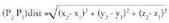 Adibidez, P(1,-2,3) eta Q(4,2,3) puntuen arteko distantziak,
honako balio hau du :
Adibidez, P(1,-2,3) eta Q(4,2,3) puntuen arteko distantziak,
honako balio hau du :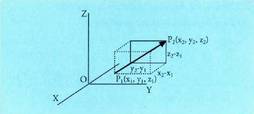 Puntu batetik plano baterako distantzia.Edozein
Puntu batetik plano baterako distantzia.Edozein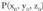 puntutatik p : Ax + By + Cz + D = 0 planora dagoen distantzia kalkulatzeko, lehenik, P puntutik pasaz planoari buruz zuta den zuzenaren ekuazioa aurkitu behar da, ondoren, zuzen horrek planoa ebakitzen duen
puntutatik p : Ax + By + Cz + D = 0 planora dagoen distantzia kalkulatzeko, lehenik, P puntutik pasaz planoari buruz zuta den zuzenaren ekuazioa aurkitu behar da, ondoren, zuzen horrek planoa ebakitzen duen puntua aurkitu eta, azkenik,
puntua aurkitu eta, azkenik, bektorearen modulua kalkulatu behar da. Kopuru hori da aurkitu nahi den distantziaren balioa.Baina bada beste prozedura bat, hori baino zuzenagoa. Planoko puntu bat, edozein, hartzen da,
bektorearen modulua kalkulatu behar da. Kopuru hori da aurkitu nahi den distantziaren balioa.Baina bada beste prozedura bat, hori baino zuzenagoa. Planoko puntu bat, edozein, hartzen da,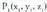 adibidez eta
adibidez eta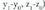 bektorearen balioa kalkulatzen da. P-tik planorako distantzia,
bektorearen balioa kalkulatzen da. P-tik planorako distantzia,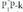 planoaren norabide normal edo perpendikularrarekiko duen proiekzioa da. Planoari buruz zuta edo normala den bektore bat
planoaren norabide normal edo perpendikularrarekiko duen proiekzioa da. Planoari buruz zuta edo normala den bektore bat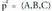 da.
da.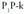 planoaren norabide normal edo perpendikularrarekiko duen proiekzioa, biderkadura eskalarra zati
planoaren norabide normal edo perpendikularrarekiko duen proiekzioa, biderkadura eskalarra zati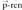 modulua da :
modulua da :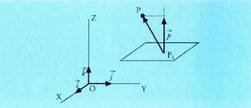 distantzia = proiekzioa =
distantzia = proiekzioa =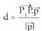 Koordenatuekin kalkulatuta :
Koordenatuekin kalkulatuta : garatuta :
garatuta :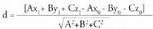 Baina
Baina planoko puntua denez, bere koordenatuek hondoko hau beteko dute :
planoko puntua denez, bere koordenatuek hondoko hau beteko dute :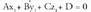 Hortik beraz,
Hortik beraz,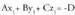 ateratzen da.Distantzia ematen duen formulan ordezkatuta :
ateratzen da.Distantzia ematen duen formulan ordezkatuta :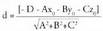 fAz+B--+C-
Distantziak beti positiboak izaten dira ; beraz, zenbakitzaileari zeinua
aldatu eta balio absolutuaren adierazpena jartzen da :
fAz+B--+C-
Distantziak beti positiboak izaten dira ; beraz, zenbakitzaileari zeinua
aldatu eta balio absolutuaren adierazpena jartzen da :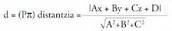 non P(x,y,z) edozein puntu den, eta formulak puntu horretatik Ax + By + Cz + D = 0 planorako distantzia ematen du.Praktikan, distantzia kalkulatzeko, planoaren ekuazioko x,y,z ezezagunak
puntuaren koordenatuez ordezkatu eta balio hori planoaren
ekuazioak dituen ezezagunen koefizienteen karratuen baturaren
erro karratuaz zatitzen da.Adibidea :1. Kalkula ezazu (1,1,1) puntutik 2x+y-2z+3=0 planorako distantzia
non P(x,y,z) edozein puntu den, eta formulak puntu horretatik Ax + By + Cz + D = 0 planorako distantzia ematen du.Praktikan, distantzia kalkulatzeko, planoaren ekuazioko x,y,z ezezagunak
puntuaren koordenatuez ordezkatu eta balio hori planoaren
ekuazioak dituen ezezagunen koefizienteen karratuen baturaren
erro karratuaz zatitzen da.Adibidea :1. Kalkula ezazu (1,1,1) puntutik 2x+y-2z+3=0 planorako distantzia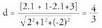 ?. Kalkula ezazu jatorri puntutik x+v+z+1=0 planorako distanl
?. Kalkula ezazu jatorri puntutik x+v+z+1=0 planorako distanl
Plano batetik beste baterako distantzia eta zuzen batetik plano baterako distantzia.
Bi planoen arteko distantzia zero da elkar ebakitzen dutenean
edota bat datozenean eta plano berbera direnean. Distantzia horrek
zero ez den balioa izan dezan, planoek paraleloak behar dute izan.
Kasu horretan, planoetako edozeinetako puntu bat hartzen da eta
beste planora dagoen distantzia kalkulatzen da.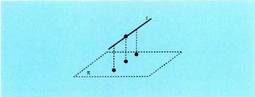 Adibidea :1. kalkulatu ondoko planoon arteko distantzia :
Adibidea :1. kalkulatu ondoko planoon arteko distantzia :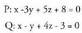 Bi planok elkar ebakitzen dute ; beraz, beren arteko distantzia zero
da.2. Kalkula ezazu ondoko planoon arteko distantzia :
Bi planok elkar ebakitzen dute ; beraz, beren arteko distantzia zero
da.2. Kalkula ezazu ondoko planoon arteko distantzia : Kasu honetan bi planoak paraleloak dira. (0,1,0) Qplanoko puntua
da. P-tik Q-rako distantzia, honako hau da :
Kasu honetan bi planoak paraleloak dira. (0,1,0) Qplanoko puntua
da. P-tik Q-rako distantzia, honako hau da :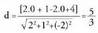 Puntu batetik zuzen baterako distantzia ere berdin kalkulatzen
da. Zuzena eta planoa paraleloak direnean bakarrik da zero. Kasu
horretan, zuzenaren edozein puntu hartzen da eta planora duen distantzia
kalkulatzen da. Horixe da zuzeneko puntu guztietatik planora
dagoen distantzia.
Puntu batetik zuzen baterako distantzia ere berdin kalkulatzen
da. Zuzena eta planoa paraleloak direnean bakarrik da zero. Kasu
horretan, zuzenaren edozein puntu hartzen da eta planora duen distantzia
kalkulatzen da. Horixe da zuzeneko puntu guztietatik planora
dagoen distantzia.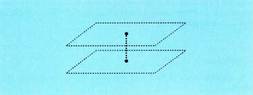 Adibidea:Kalkulatu (x,y,z) = (0,1,2)+t(-4,1,3) zuzenetik 3x+4z-3=0 planora
dagoen distantzia. Zuzena eta planoa paraleloak dira. (0,1,2)
zuzeneko puntua da eta planora duen distantzia honako hau da :
Adibidea:Kalkulatu (x,y,z) = (0,1,2)+t(-4,1,3) zuzenetik 3x+4z-3=0 planora
dagoen distantzia. Zuzena eta planoa paraleloak dira. (0,1,2)
zuzeneko puntua da eta planora duen distantzia honako hau da :
Puntu batetik zuzen baterako distantzia.
Puntu batetik zuzen baterako distantzia kalkulatzeko, biderkadura
bektorialak erabiltzen duen formula ere erabil daiteke ; baina maiz
askoz ere errazagoa da urrats gehiago baina errazagoak dituzten
beste metodo batzuek erabiltzea.Kalkula dezagun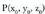 puntutik
puntutik zuzenera dagoen distantzia.
zuzenera dagoen distantzia.
Formula orokorra ikustetik hasita : eta
eta aldeak dituen paralelogramoaren azalera,
aldeak dituen paralelogramoaren azalera,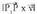 da, baina bestalde, oina bider altura da eta oina
da, baina bestalde, oina bider altura da eta oina bada, altura eskatutako distantzia da. Hortik beraz,
bada, altura eskatutako distantzia da. Hortik beraz,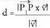 da. Zehatzago emanda:
da. Zehatzago emanda: Adibideak:
1. Kalkulatu P(1,1,1) puntutik r zuzenerako distantzia ; r:
Adibideak:
1. Kalkulatu P(1,1,1) puntutik r zuzenerako distantzia ; r: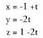 Zuzenaren norabide bektorea
Zuzenaren norabide bektorea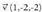 da eta R(1,0,1) bertako puntu bat. P puntua eta R puntua elkartzen dituen bektorea
da eta R(1,0,1) bertako puntu bat. P puntua eta R puntua elkartzen dituen bektorea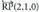 da, eta ekuazioan esplizituki aurkitzen da.Lehengo formula, era honetan erabiliko da :
da, eta ekuazioan esplizituki aurkitzen da.Lehengo formula, era honetan erabiliko da :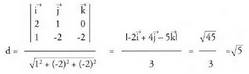 2. Ariketa bera beste metodo baten bidez. r zuzenari buruz zuta izanik P puntutik igarotzen den planoa aurkitzen da. r zuzenarekin duen S ebaki puntua kalkulatzen da. PS da eskatutako distantzia.
2. Ariketa bera beste metodo baten bidez. r zuzenari buruz zuta izanik P puntutik igarotzen den planoa aurkitzen da. r zuzenarekin duen S ebaki puntua kalkulatzen da. PS da eskatutako distantzia.
Aurkitu nahi den planoak bektore perpendikularra du, zuzenaren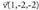 norabide bektore dena. Beraz, aurkitu nahi den planoak P(1,1,1) puntua bere barne du eta v-ri buruz zuta da ; beraz, planoaren ekuazioa (x-1)-2(y-1)-2(z-1) = 0 da.
norabide bektore dena. Beraz, aurkitu nahi den planoak P(1,1,1) puntua bere barne du eta v-ri buruz zuta da ; beraz, planoaren ekuazioa (x-1)-2(y-1)-2(z-1) = 0 da.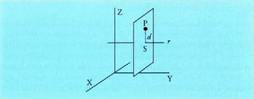 Horrek r zuzenarekin duen ebaki puntua kalkulatuko dugu. r:
Horrek r zuzenarekin duen ebaki puntua kalkulatuko dugu. r: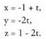 Zuzenean x,y,z dituzten balioak planoaren ekuazioan ordezkatuz
lortzen da ebaki puntu hori : (-1+t-1)-2(2t-1)-2(2(1-2t-1) = 0
Zuzenean x,y,z dituzten balioak planoaren ekuazioan ordezkatuz
lortzen da ebaki puntu hori : (-1+t-1)-2(2t-1)-2(2(1-2t-1) = 0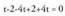 Emaitza : t = 0. Zuzenak plano hori ebakitzen duen puntua, R(-1,0,1) da eta bektorea
Emaitza : t = 0. Zuzenak plano hori ebakitzen duen puntua, R(-1,0,1) da eta bektorea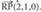 Beraz, aurkitu nahi den distantzia :
Beraz, aurkitu nahi den distantzia :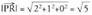 3. Ebazteko beste modu bat, deribatuez baliatzea da, era honetara. Zuzenaren edozein puntutatik P punturako distantzia,
3. Ebazteko beste modu bat, deribatuez baliatzea da, era honetara. Zuzenaren edozein puntutatik P punturako distantzia,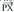 bektorearen modulua da, X zuzeneko edozein puntu delarik. Zuzenaren ekuazioa honako hau denez :
bektorearen modulua da, X zuzeneko edozein puntu delarik. Zuzenaren ekuazioa honako hau denez : bektorearen moduluaren baliorik txikiena
bektorearen moduluaren baliorik txikiena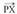 adierazpenak baliorik txikiena duenean da. Analisian, zera jakin da, alegia, funtzio deribagarri batek bere balio txikiena (minimoa) deribatua zero bihurtzen den puntu batean duela.
adierazpenak baliorik txikiena duenean da. Analisian, zera jakin da, alegia, funtzio deribagarri batek bere balio txikiena (minimoa) deribatua zero bihurtzen den puntu batean duela.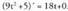 " alt="" id="pint0" />. Beraz, deribatua, t=O denean da zero ; beraz, P-tik distantziarik txikienera dagoen zuzeneko puntua R(-1,0,1) da, eta ariketaren gainerako zatia aurreko adibidean bezala ebazten da.4. Perpendikulartasuna erabil daitekeen beste prozed ura bat hau da. P puntua r zuzeneko puntuekin elkartuz lortutako
" alt="" id="pint0" />. Beraz, deribatua, t=O denean da zero ; beraz, P-tik distantziarik txikienera dagoen zuzeneko puntua R(-1,0,1) da, eta ariketaren gainerako zatia aurreko adibidean bezala ebazten da.4. Perpendikulartasuna erabil daitekeen beste prozed ura bat hau da. P puntua r zuzeneko puntuekin elkartuz lortutako " alt="" id="pint0" />bektoreetatik, zuzenari buruz zuta dena da laburrena. Beraz, punturik hurbilenarentzat
" alt="" id="pint0" />bektoreetatik, zuzenari buruz zuta dena da laburrena. Beraz, punturik hurbilenarentzat bektorea zuzenaren
bektorea zuzenaren norabide bektoreari buruz zuta da. Bi bektore elkartzutak dira, baldin eta beren biderkadura
eskalarra zero bada. Horren ondorioz :
norabide bektoreari buruz zuta da. Bi bektore elkartzutak dira, baldin eta beren biderkadura
eskalarra zero bada. Horren ondorioz :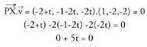
Bi zuzenen arteko distantzia.
Zuzenek elkar ebakitzen badute, distantzia zero da. Zero ez den
distantzia izateko aukerak, paraleloak izatea edota elkar gurutzatzea
dira.a) Zuzenak paraleloak badira, horietako bateko edozein puntu
hartzen da, eta handik bestera dagoen distantzia kalkulatzen, puntu
batetik zuzen baterako distantzia kalkulatzeko ikusitako sistemen
arabera.b) Zuzenek elkar gurutzatzen badute, ez dira jakinak beren arteko
gutxieneko distantzia zehazten duten bi puntuak. Distantzia txikien
edo minimo hori kalkulatzeko, bien perpendikularra den zuzena
kalkulatuz has daiteke, eta, hartatik abiatuta, distantziarik
txikiena edo minimoa aurkitu, edota biderkadura bektoriala erabili
.b.1. Emandako bi zuzenei buruz zuta den zuzena aurkitzeko,
zuzenetako bateko puntu bat eta besteko beste bat elkartuko dituen
bektore orokor baten koordenatuak kalkulatzetik hasten da. Bektore
orokor komun hori bi parametroen baitakoa izango da, zuzen
bakoitzeko bat.Bektore hori bi zuzenen norabide bektoreei buruz zuta izan dadila
eskatuz, bi ekuazio ateratzen dira eta horien bitartez lortzen da
bien perpendikular komuna igarotzen den puntuetako koordenatuak
ematen dituzten bi parametroen balioak kalkulatzea.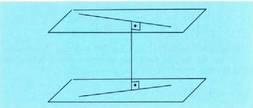 Adibidea:Kalkula ezazu honako bi zuzen hauen arteko distantzia :
Adibidea:Kalkula ezazu honako bi zuzen hauen arteko distantzia : Bi zuzenetako parametroei, ez nahastearren, izen desberdinak ematen zaizkie. Zuzen bateko puntu bat besteko edozein punturekin elkartzen duen
Bi zuzenetako parametroei, ez nahastearren, izen desberdinak ematen zaizkie. Zuzen bateko puntu bat besteko edozein punturekin elkartzen duen bektorea zera da :
bektorea zera da : .
.
Zuzenen norabide bektoreak honako hauek dira :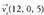 eta
eta perpendikularra izan dadin, bi bektore horien biderkadura eskalarrak zero izan behar du :
perpendikularra izan dadin, bi bektore horien biderkadura eskalarrak zero izan behar du :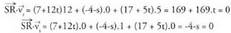 Emaitzak t = - 1 eta s = 4 dira ; beraz, perpendikular komuna igarotzen
den zuzen bakoitzeko puntuak P (1,2,3) eta P s (6,2,-9) dira,
eta elkarren arteko distantzia honako hau izango da :
Emaitzak t = - 1 eta s = 4 dira ; beraz, perpendikular komuna igarotzen
den zuzen bakoitzeko puntuak P (1,2,3) eta P s (6,2,-9) dira,
eta elkarren arteko distantzia honako hau izango da :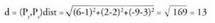 b.2. Biderkadura bektoriala erabiliz, hau da metodoa : zuzen
bakoitzaren norabide bektoreak hartzen dira eta zuzen bateko edozein
puntu beste zuzeneko beste edozeinekin elkartuko duen bektorea
. Eratzen duten paralelepipedoaren bolumena, oinaren azalera
bider altura da eta kasu honetan altura, bi zuzenen artean dagoen
eta aurkitu nahi dugun distantziarekin bat dator. Bolumena ordea,
biderkadura mistoa da, eta oinaren azalera bere aldeen biderkadura
bektoriala da ; beraz, distantzia, bien arteko zatiketa moduan lor
daiteke.
b.2. Biderkadura bektoriala erabiliz, hau da metodoa : zuzen
bakoitzaren norabide bektoreak hartzen dira eta zuzen bateko edozein
puntu beste zuzeneko beste edozeinekin elkartuko duen bektorea
. Eratzen duten paralelepipedoaren bolumena, oinaren azalera
bider altura da eta kasu honetan altura, bi zuzenen artean dagoen
eta aurkitu nahi dugun distantziarekin bat dator. Bolumena ordea,
biderkadura mistoa da, eta oinaren azalera bere aldeen biderkadura
bektoriala da ; beraz, distantzia, bien arteko zatiketa moduan lor
daiteke.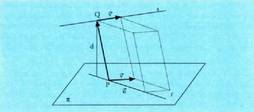 Adibidea :Biderkadura bektoriala erabiliz, kalkulatu aurreko adibidean
aztertutako bi zuzenen arteko distantzia :
Adibidea :Biderkadura bektoriala erabiliz, kalkulatu aurreko adibidean
aztertutako bi zuzenen arteko distantzia : Norabide bektoreak
Norabide bektoreak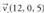 eta
eta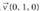 dira. Zuzen bateko puntu bat eta besteko beste bat elkartzen dituen bektore bat (13,2,8) - (6,6,-9) = (7,-4,17). Orduan distantzia :
dira. Zuzen bateko puntu bat eta besteko beste bat elkartzen dituen bektore bat (13,2,8) - (6,6,-9) = (7,-4,17). Orduan distantzia : Metodo hau zuzenagoa da, baina honekin ezin daiteke kalkulatu
perpendikular komunaren ekuazioa.Paralelepipedoaren eta tetraedroaren bolumena.ABCDEFGH erpinak dituen paralelepipedoa baldin badugu eta
haren bolumena kalkulatu nahi badugu, erpin berean elkartzen
diren hiru ertz edo alderi dagozkien hiru bektore aurkituko ditugu,
AB, AD eta AE adibidez. Hiru bektore horien biderkadura mistoa,
paralelepipedoaren bolumena izango da.Adibidea :ABCDEFGH paralelepipedoak, honako erpin hauek ditu : A(0,0,0), B(1,0,0), C(2,1,0), D (1,1,0), E(1,0,1), F(2,0,1), G(3,1,1) eta H(2,1,1). Kalkulatu paralelepipedo horren bolumena.
Metodo hau zuzenagoa da, baina honekin ezin daiteke kalkulatu
perpendikular komunaren ekuazioa.Paralelepipedoaren eta tetraedroaren bolumena.ABCDEFGH erpinak dituen paralelepipedoa baldin badugu eta
haren bolumena kalkulatu nahi badugu, erpin berean elkartzen
diren hiru ertz edo alderi dagozkien hiru bektore aurkituko ditugu,
AB, AD eta AE adibidez. Hiru bektore horien biderkadura mistoa,
paralelepipedoaren bolumena izango da.Adibidea :ABCDEFGH paralelepipedoak, honako erpin hauek ditu : A(0,0,0), B(1,0,0), C(2,1,0), D (1,1,0), E(1,0,1), F(2,0,1), G(3,1,1) eta H(2,1,1). Kalkulatu paralelepipedo horren bolumena.
Erpinak ordenan eman direla suposatuta, A-n elkartzen diren hiru ertzak edo aldeak, AB, AD eta AE dira. Hiru ertz horien araberako bektoreak berriz honako hauek :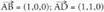 eta
eta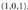 Jakin nahi den bolumena beraz, honako hau da :
Jakin nahi den bolumena beraz, honako hau da :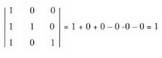 Tetraedroa baldin bada, hiru ertzak berdinak dituen paralelepipedoaren
seirena du bolumena. Hain zuzen ere, tetraedroa piramidetzat
har daiteke eta piramidearen bolumena, oinarri eta altura berdinetako
prismak duenaren herena da. Bestalde, tetraedroaren
oinarria triangelua da eta paralelepipedoaren oinarri den eta alde
berdin nahiz horien artean eratutako angelu bera dituen paralelogramoak
duen azaleraren erdia du. Beraz, tetraedroaren bolumena,
erpin berean elkartzen diren hiru ertz edo aldeei dagozkien hiru
bektoreen biderkadura mistoaren seirena da. Tetraedroa ABCD
baldin bada :
Tetraedroa baldin bada, hiru ertzak berdinak dituen paralelepipedoaren
seirena du bolumena. Hain zuzen ere, tetraedroa piramidetzat
har daiteke eta piramidearen bolumena, oinarri eta altura berdinetako
prismak duenaren herena da. Bestalde, tetraedroaren
oinarria triangelua da eta paralelepipedoaren oinarri den eta alde
berdin nahiz horien artean eratutako angelu bera dituen paralelogramoak
duen azaleraren erdia du. Beraz, tetraedroaren bolumena,
erpin berean elkartzen diren hiru ertz edo aldeei dagozkien hiru
bektoreen biderkadura mistoaren seirena da. Tetraedroa ABCD
baldin bada : Adibidea :KalkulaezazuA(1,0,0), B(0,1,1), C(1,0,1) eta D(1,1,0) erpintzat
dituen tetraedroaren bolumena.A-n elkartzen diren hiru aldeak, honako hauek dira :
Adibidea :KalkulaezazuA(1,0,0), B(0,1,1), C(1,0,1) eta D(1,1,0) erpintzat
dituen tetraedroaren bolumena.A-n elkartzen diren hiru aldeak, honako hauek dira :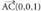 eta
eta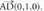 Beraz, kalkulatu nahi den bolumena :
Beraz, kalkulatu nahi den bolumena :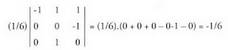
- Ariketak
26. Kalkulatu P(1,1,1) puntutik 2x+2y-z+3=0 planorako distantzia.27. Kalkulatu P(0,2, 1) puntutik (x,yz) = (1,0,1) +t(1,-1,1) zuzenerako distantzia.28. Kalkulatu x+y-2z+1=0 eta 2x+2y-z+3=0 planoen arteko distantzia.29. Kalkulatu (x-2)/1 = y/2 = (z+1)/2 eta (x,yz) = (0,0,1) + t(2,0,2) zuzenen arteko distantzia.30. Kalkulatu erpinak A(1,0,0), B(2,1,0), C(1,2,0) eta D(0,0,2) puntuak dituen tetraedroaren bolumena.
XI. Proiekzio ortogonala eta simetria.
Puntu batek zuzen batean duen proiekzioa jakiteko, puntu horretatik
igaro eta zuzenari buruz zuta den planoa zein den kalkulatu
behar da. Plano horrek eta zuzenak elkarren artean duten ebaki
puntua, huraxe da aurkitu nahi den proiekzioa.Puntu batek planoan duen proiekzioa aurkitzeko, puntutik igaro
eta planoari buruz zuta den zuzen perpendikularra aurkitzen da.
Zuzen horren eta planoaren arteko ebaki puntua, aurkitu nahi
dugun puntua da.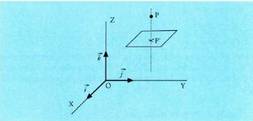 Zuzen batek plano batean duen proiekzioa jakiteko, bi punturen
proiekzioa aurki daiteke eta elkartzen dituen zuzenaren ekuazioa
aurkitu. Zuzena barne duen eta hori proiektatu nahi den planoari
buruz zuta den planoaren ekuazioa aurkituta ere egin daiteke. Plano
horrek eman den planoarekin duen ebakidura da proiekzio den
zuzena.Adibidea.1. Kalkula ezazu P(1,0,1) puntuak r : (x,y,z) = (0,3,1) + t(1,2,1)
zuzenean duen proiekzioa. P barne duen eta r-ri buruz zuta den planoak,
honako ekuazio hau du :
Zuzen batek plano batean duen proiekzioa jakiteko, bi punturen
proiekzioa aurki daiteke eta elkartzen dituen zuzenaren ekuazioa
aurkitu. Zuzena barne duen eta hori proiektatu nahi den planoari
buruz zuta den planoaren ekuazioa aurkituta ere egin daiteke. Plano
horrek eman den planoarekin duen ebakidura da proiekzio den
zuzena.Adibidea.1. Kalkula ezazu P(1,0,1) puntuak r : (x,y,z) = (0,3,1) + t(1,2,1)
zuzenean duen proiekzioa. P barne duen eta r-ri buruz zuta den planoak,
honako ekuazio hau du :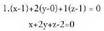 Izan ere, bektore perpendikularra
Izan ere, bektore perpendikularra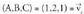 , eta P- tik pasa behar baitu.Proiekzioa plano horren eta r-ren arteko ebakidura da :
, eta P- tik pasa behar baitu.Proiekzioa plano horren eta r-ren arteko ebakidura da :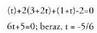 Puntuaren proiekzio puntua
Puntuaren proiekzio puntua 2. Kalkula ezazu P(2,-1,1) puntuak x-y+2z+1=0 planoan duen
proiekzioa. P-tik igaro eta planoari buruz zuta den planoa honako
hau da: (x,yz) = (2,-1,1) + t(1,-1,2), izan ere, (A,B,C) ezezagunen
koefizienteek eratutako bektorea zuta baita planoari buruz.Horrek planoarekin duen ebakidura, planoaren x,y,z, zuzenean
parametroaren arabera dituzten balioez ordezkatuz aurkitzen da :
2. Kalkula ezazu P(2,-1,1) puntuak x-y+2z+1=0 planoan duen
proiekzioa. P-tik igaro eta planoari buruz zuta den planoa honako
hau da: (x,yz) = (2,-1,1) + t(1,-1,2), izan ere, (A,B,C) ezezagunen
koefizienteek eratutako bektorea zuta baita planoari buruz.Horrek planoarekin duen ebakidura, planoaren x,y,z, zuzenean
parametroaren arabera dituzten balioez ordezkatuz aurkitzen da :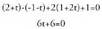 Beraz, t=-1 da eta
Beraz, t=-1 da eta Beraz, t=-1 da eta3. Kalkula ezazu r : (x-1)/1 = (y+1)/l = z/(-2) zuzenak x+y+z-1=0
planoan duen proiekzioa.Zuzena barne duen eta eman den planoari buruz zuta den planoa
zuzenaren bektore ekuaziotik lortzen da planoarekiko norabide perpendikularrean
(1,l,1) bektore sortzailea erantsiz :
Beraz, t=-1 da eta3. Kalkula ezazu r : (x-1)/1 = (y+1)/l = z/(-2) zuzenak x+y+z-1=0
planoan duen proiekzioa.Zuzena barne duen eta eman den planoari buruz zuta den planoa
zuzenaren bektore ekuaziotik lortzen da planoarekiko norabide perpendikularrean
(1,l,1) bektore sortzailea erantsiz :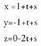 Era orokorrera pasaz, hau gelditzen da: x-y=2x-y=2 eta x+y+z-I=0 planoen arteko ebakidura den zuzena da
emaitza.Zuzen horren bektore ekuazioa nahi baldin bada, bi plano horietakoa
den edozein punturen koordenatuak kalkulatzen dira ; bedi
(2,0,-1) adibidez. Zuzenaren norabide bektorea kalkulatzeko, kontuan
hartu behar da planoetako bakoitzari buruz zutak diren bi bektoreei
buruz zuta dela. Biei buruz zuta den bektorea beren biderkadura
bektoriala da. Halere ordea, errazagoa da ezezagun bat x=t
parametroaren berdintzat hartu eta gainerakoen balioak kalkulatzea
:
Era orokorrera pasaz, hau gelditzen da: x-y=2x-y=2 eta x+y+z-I=0 planoen arteko ebakidura den zuzena da
emaitza.Zuzen horren bektore ekuazioa nahi baldin bada, bi plano horietakoa
den edozein punturen koordenatuak kalkulatzen dira ; bedi
(2,0,-1) adibidez. Zuzenaren norabide bektorea kalkulatzeko, kontuan
hartu behar da planoetako bakoitzari buruz zutak diren bi bektoreei
buruz zuta dela. Biei buruz zuta den bektorea beren biderkadura
bektoriala da. Halere ordea, errazagoa da ezezagun bat x=t
parametroaren berdintzat hartu eta gainerakoen balioak kalkulatzea
: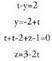 Eta hortik ateratzen da :
Eta hortik ateratzen da :
Puntu batek zuzen batekiko edota plano batekiko duen simetri puntua.
Proiekzioa ezagututa, jatorrizko puntuaren eta simetrikoa izan
behar duenaren arteko erdiko puntuak aurkitutako proiekzioa izan
behar duela kontuan hartuz kalkulatzen da simetri puntua edo
puntu simetrikoa. Adibidea:1. Kalkulaezazu P(1,0,1) puntuak (x,yz) = (0,3,1) + t(1,2,1) zuzenarekiko
duen simetri puntua.Puntu batek zuzen batean duen proiekzioa aurkitzeko moduaz iharduten zuen lehen adibidean, puntu horrek zuzenean duen proiekzio puntua
Adibidea:1. Kalkulaezazu P(1,0,1) puntuak (x,yz) = (0,3,1) + t(1,2,1) zuzenarekiko
duen simetri puntua.Puntu batek zuzen batean duen proiekzioa aurkitzeko moduaz iharduten zuen lehen adibidean, puntu horrek zuzenean duen proiekzio puntua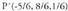 dela lortu da.Horren simetrikoak hauek bete beharko ditu :
dela lortu da.Horren simetrikoak hauek bete beharko ditu : Beraz, simetri puntua,
Beraz, simetri puntua,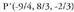 2.2. Kalkulatu P(2,-1,1) puntuakx-y+2z+1=0 planoarekiko duen simetri puntua.Proiekzioei buruzko atal honetako 2. adibidean, puntu horrek plano horrekiko duen proiekzio puntua
2.2. Kalkulatu P(2,-1,1) puntuakx-y+2z+1=0 planoarekiko duen simetri puntua.Proiekzioei buruzko atal honetako 2. adibidean, puntu horrek plano horrekiko duen proiekzio puntua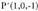 dela ikusi da.Beraz, puntu simetrikoa hau izango da :
dela ikusi da.Beraz, puntu simetrikoa hau izango da : Beraz, simetri puntua
Beraz, simetri puntua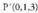
- Ariketak
3 1. Kalkulatu ondoko elementuokiko P(1,-1,-1) puntuak duen proiekzioa eta simetri puntua :a) x+y-2z-1=O planoarekiko etab) (x,yz) = (2,-2,1) + t(1,0,-2) zuzenarekiko.
XII. Zuzenki baten erdibitzailea eta angelu diedro baten erdikaria.
Atal honetan, zuzenki baten plano erdibitzailea eta diedro baten
plano erdikaria aztertuko dira, hain zuzen ere, espazioan ekuazio
soila duten hi leku geometriko direnak.Erdibitzailea.Zuzenki baten erdibitzailea, muturretatik distantzia berdinera dauden edota distantziakide diren puntuen leku geometrikoa da.
Emandako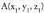 eta
eta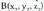 puntuetatik distantzia berdinera dauden puntuen leku geometrikoa kalkulatzeko, ezaguntzat jotzen da leku geometrikoaren P(x,y,z) puntua eta P puntutik A eta B puntuetarako distantziak berdinak izateko baldintza ezartzen zaio :
puntuetatik distantzia berdinera dauden puntuen leku geometrikoa kalkulatzeko, ezaguntzat jotzen da leku geometrikoaren P(x,y,z) puntua eta P puntutik A eta B puntuetarako distantziak berdinak izateko baldintza ezartzen zaio :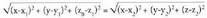 Karratua eginez eta sinplifikatuta, honela gelditzen da :
Karratua eginez eta sinplifikatuta, honela gelditzen da :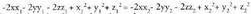 Hau da, honako ekuazio hau duen planoa :
Hau da, honako ekuazio hau duen planoa :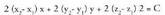 non C zenbaki erreala den, A eta B puntuen koordenatuen batuketa
eta kenketen karratuek emandako emaitza.
non C zenbaki erreala den, A eta B puntuen koordenatuen batuketa
eta kenketen karratuek emandako emaitza.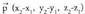 bektorea zuta da planoari buruz. Beraz, zuzenki baten erdibitzailea zuzenki horri buruz zuta den planoa da.
bektorea zuta da planoari buruz. Beraz, zuzenki baten erdibitzailea zuzenki horri buruz zuta den planoa da.
Kalkulu soil baten bitartez egiazta daiteke, alegia, AB-ren erdiko puntua,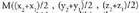 plano erdibitzailekoa dela. Beraz, zuzenki baten erdibitzailea zuzenki horren erdiko puntutik igarotzen den plano perpendikular moduan defini daiteke.Adibidea.Kalkula ezazu AB zuzenkiaren erdibitzailea, A(O,O,O) eta B(2,2,2)
izanda. Egiazta ezazu erdiko puntua plano erdibitzailekoa dela.
plano erdibitzailekoa dela. Beraz, zuzenki baten erdibitzailea zuzenki horren erdiko puntutik igarotzen den plano perpendikular moduan defini daiteke.Adibidea.Kalkula ezazu AB zuzenkiaren erdibitzailea, A(O,O,O) eta B(2,2,2)
izanda. Egiazta ezazu erdiko puntua plano erdibitzailekoa dela.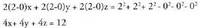 Sinplifikatuta :
Sinplifikatuta :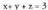
Angelu diedroaren erdikaria.
Angelu diedroaren plano erdikaria diedroa beste bitan zatitzen
duen planoa da. Diedroaren aldeetatik distantziakide diren puntuen
leku geometrikoarekin bat dator.Diedroa elkar ebakitzen duten bi planok eratzen badute , Ax + By + + Cz + D = 0 eta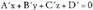 planoek adibidez, leku geometriko horretako P(x,y,z) edozein puntuk, bi planoetara distantzia berbera delako baldintza beteko du. Puntu batetik plano baterako distantzia honako hau da :
planoek adibidez, leku geometriko horretako P(x,y,z) edozein puntuk, bi planoetara distantzia berbera delako baldintza beteko du. Puntu batetik plano baterako distantzia honako hau da :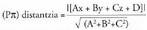 Beraz, baldintza hori, ondorengo ekuazio honetara bihurtzen da :
Beraz, baldintza hori, ondorengo ekuazio honetara bihurtzen da : Balio absolutuen zeinuak kenduta, barneko eta kanpoko erdikarien bi ekuazioak gelditzen dira :Adibidea.Aurki ezazu z = 0 eta y = 0 planoen plano erdikaria
Balio absolutuen zeinuak kenduta, barneko eta kanpoko erdikarien bi ekuazioak gelditzen dira :Adibidea.Aurki ezazu z = 0 eta y = 0 planoen plano erdikaria
- Ariketak
32. Kalkula ezazu A(1,0,-3) eta B(1,2,-1) puntuen arteko zuzenkiaren erdibitzailearen ekuazioa.33. Kalkula ezazu x-2y-2z+3=0 eta 3x+4y+5=0 planoen erdikariaren ekuazioa.
XIII. Esfera.
Esfera, zentro deritzon puntu finko batetik distantziakide diren espazioko puntuen multzoari esaten zaio, eta puntu horiek zentrora duten distantzia komun horri esferaren erradio deitzen zaio. Bedi P(x,yz) esferaren edozein puntu. zentroa baldin bada e ta erradioak r neurtzen badu, definizio h orrek, esferaren puntuek hau bete dezatela eskatzen du :
zentroa baldin bada e ta erradioak r neurtzen badu, definizio h orrek, esferaren puntuek hau bete dezatela eskatzen du :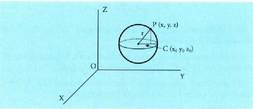 Karratua eginez:
Karratua eginez: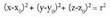 Garatuta:
Garatuta: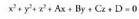 non :
non :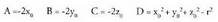 Azken berdintza hauek, esfera baten ekuazioa emanda, haren zentroa
eta erradioa kalkulatzeko aukera ematen dute.Adibidea.1. Kalkula ezazu C(1,0,1) zentrotzat eta erradioa 2 dituen esferaren
ekuazioa.
Azken berdintza hauek, esfera baten ekuazioa emanda, haren zentroa
eta erradioa kalkulatzeko aukera ematen dute.Adibidea.1. Kalkula ezazu C(1,0,1) zentrotzat eta erradioa 2 dituen esferaren
ekuazioa.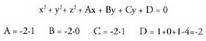 Beraz,
Beraz,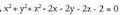 Alderantziz, hiru ezezaguneko eta bigarren mailako polinomio orokor bat,
Alderantziz, hiru ezezaguneko eta bigarren mailako polinomio orokor bat,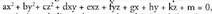 , esferaren ekuazio izan dadin, a=b=c eta d=e=f=O izan behar dute.
, esferaren ekuazio izan dadin, a=b=c eta d=e=f=O izan behar dute.
Gainera, erradioa erreala izan behar du, hots :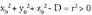 baino
Esferak ondoko ekuazioa badu :
baino
Esferak ondoko ekuazioa badu :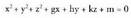 esfera erreala da baldin eta :
esfera erreala da baldin eta :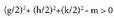
- Ariketak
34. Kalkula itzazu ondorengo esferen ekuazioak :a) Zentroa C(1,-3,4) puntuan eta r = 3 dituenarena.b) Diametroaren muturrak A(-1,2,5) eta B(3,4,5) puntuetan dituenarena.35. Adieraz ezazu ea ondorengo ekuazioen artean zeintzuk irudikatzen dituzten esferak. Esferak direnean, kalkulatu zentroaren koordenatuak eta erradioa. :
13.1. Lau puntuk zehaztutako esfera.
Planokide ez diren lau puntu emanik, esfera bat eta bakarra zehazten dute eta esfera hori puntu horietatik igarotzen da. Bitez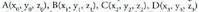 esferaren ekuazioa bete ?ekar duten lau puntuak. Orduan, honako hau izango dugu :
esferaren ekuazioa bete ?ekar duten lau puntuak. Orduan, honako hau izango dugu :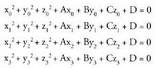
- Ariketak
36. Kalkulatu A(O,O,1), B(-1,0,2), C(0,2,0) eta D(2,2,2) puntuetatik igarotzen den esferaren ekuazioa.
13.2. Puntu batek esferarekiko duen posizioa.
Esferaren ekuazioa :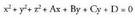 .
.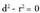 egitetik dator, d esferaren azalean dagoen P puntutik esferaren zentroraino dagoen distantzia delarik. Esferaren azaleandagoen puntu baten koordenatuak esferaren barruan dagoen puntu
baten koordenatuez ordezkatuz gero, d < r baino izango denez, esferaren
ohiko ekuazioaren adierazpenak negatiboa eman beharko
luke. d > r baino izanda, esferaz kanpoko puntu baten koordenatuak
hartuz gero, ekuazioak positibo emango luke zero eman ordez.Beraz, puntu bat esferaren barruan, esfera azalean ala kanpoan
dagoen jakiteko, aski da puntuaren koordenatuak esferaren ekuazioan
ordezkatu eta ematen duen emaitza begiratzea. Emaitza positiboa
baldin bada, puntua esferaz kanpo dago, zero ematen badu
esferaren azalean dago, eta negatiboa baldin bada, esferaren barruan
dago.Adibidea:Esan ea A(2,4,0), B(0,0,1), C(2,3,3) eta D(-1,1,4) puntuak esferaren
kanpoan, esfera azalean edota esferaren barruan dauden.
egitetik dator, d esferaren azalean dagoen P puntutik esferaren zentroraino dagoen distantzia delarik. Esferaren azaleandagoen puntu baten koordenatuak esferaren barruan dagoen puntu
baten koordenatuez ordezkatuz gero, d < r baino izango denez, esferaren
ohiko ekuazioaren adierazpenak negatiboa eman beharko
luke. d > r baino izanda, esferaz kanpoko puntu baten koordenatuak
hartuz gero, ekuazioak positibo emango luke zero eman ordez.Beraz, puntu bat esferaren barruan, esfera azalean ala kanpoan
dagoen jakiteko, aski da puntuaren koordenatuak esferaren ekuazioan
ordezkatu eta ematen duen emaitza begiratzea. Emaitza positiboa
baldin bada, puntua esferaz kanpo dago, zero ematen badu
esferaren azalean dago, eta negatiboa baldin bada, esferaren barruan
dago.Adibidea:Esan ea A(2,4,0), B(0,0,1), C(2,3,3) eta D(-1,1,4) puntuak esferaren
kanpoan, esfera azalean edota esferaren barruan dauden.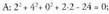 ; beraz, esfera azalean dago.
; beraz, esfera azalean dago.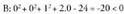 baino ; beraz, esfera barruan dago.
baino ; beraz, esfera barruan dago.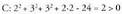
- Ariketak
37. Aurkitu A(1,0,0), B(0,1,-1), C(1,-1,0), D(1,1,1), E(1,2,0), F(0,0,0) eta puntuek
puntuek
13.3. Esferaren eta planoaren arteko ebakidura.
Esferaren zentrotik planoa zernolako distantziara dagoenaren arabera,
planoa, esferaz kanpo egon daiteke, zentrotik erradioa baino
distantzia handiagora badago ; esferaren ukitzaile izan daiteke erradioa
adinako distantziara badago, edota ebakitzailea izan daiteke
erradioa baino distantzia txikiagora badago.Esferarekiko ukitzaile den planoa ukitze puntura doan erradioaren
perpendikularra da. Plano batek esfera bat ebakitzen badu, sekzioa
edo epaia zirkulua da (azalarena zirkunferentzia) eta planoari
buruz zuta den esferaren erradioa haren zentrotik igarotzen da.
Esferaren zentrotik plano ebakitzailerako distantzia d baldin bada
eta esferaren erradioa r, epai zirkuluaren r erradioak eta esferarenak,
erlazio hau dute :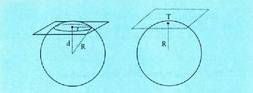 Esfera baten eta zuzen baten arteko ebakidura.
Zuzena esferaz kanpokoa da, baldin esferaren zentrotik erradioa baino dinstantzia handiagora badago. Ukitzailea da distantziahori n erradioaren berdina bada, eta ebakitzailea, zentrotik zuzenerako
distantzia erradioa baino txikiagoa bada.Esferaren eta zuzenaren ekuazioak emanik, sistema ebatz daiteke,
eta bi emaitza, emaitza bakarra ala emaitzarik bat ere ez den, zuzena
ebakitzailea, ukitzailea ala esferaz kanpokoa izango da. Zuzen ebakitzaile
batek, bi puntu komun ditu esfera azalarekin, zuzen ukitzaileak
bat eta kanpoko zuzenak bat ere ez.Adibidea:Erreferentzia ortonormaleko hiru dimentsiotako espazio euklidear
batean, S esfera daukagu ondorengo ekuazioarekin :
Esfera baten eta zuzen baten arteko ebakidura.
Zuzena esferaz kanpokoa da, baldin esferaren zentrotik erradioa baino dinstantzia handiagora badago. Ukitzailea da distantziahori n erradioaren berdina bada, eta ebakitzailea, zentrotik zuzenerako
distantzia erradioa baino txikiagoa bada.Esferaren eta zuzenaren ekuazioak emanik, sistema ebatz daiteke,
eta bi emaitza, emaitza bakarra ala emaitzarik bat ere ez den, zuzena
ebakitzailea, ukitzailea ala esferaz kanpokoa izango da. Zuzen ebakitzaile
batek, bi puntu komun ditu esfera azalarekin, zuzen ukitzaileak
bat eta kanpoko zuzenak bat ere ez.Adibidea:Erreferentzia ortonormaleko hiru dimentsiotako espazio euklidear
batean, S esfera daukagu ondorengo ekuazioarekin :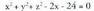 eta P planoa ondorengo ekuazioak definituta : 2x - y + 2z + 7 = 0.
eta P planoa ondorengo ekuazioak definituta : 2x - y + 2z + 7 = 0.
Honako hauek egitea eskatzen da :a) Kalkulatu P planoari buruz paralelo izanik, S esferarekiko ukitzaileak diren eta
eta plano ukitzaileen ekuazioak.b) Kalkulatu S esferaren eta P planoaren ebakidura den c zirkuluaren
erradioa eta bere zentroaren koordenatuak.c) Kalkulatu c zirkulua eta bere zirkunferentzia barne dituen eta
ahalik eta erradiorik txikiena duen esferaren ekuazioa.d) Kalkulatu S esferarekiko A(-11/3, -5/3, -2/3) puntuan ukitzaile
izan behar duen eta P planokoa den zuzenaren ekuazioa.Ebazpena :a) P-ri buruz paraleloak izateagatik, bere ekuazioa 2x-y+2z+d=0
izango da.Esferaren zentroa C(1,0,0) da eta bere erradioa r = 5.C-tik plano ukitzaile horietarako distantziak 5 balio behar du, hori baita erradioaren luzera ; beraz:
plano ukitzaileen ekuazioak.b) Kalkulatu S esferaren eta P planoaren ebakidura den c zirkuluaren
erradioa eta bere zentroaren koordenatuak.c) Kalkulatu c zirkulua eta bere zirkunferentzia barne dituen eta
ahalik eta erradiorik txikiena duen esferaren ekuazioa.d) Kalkulatu S esferarekiko A(-11/3, -5/3, -2/3) puntuan ukitzaile
izan behar duen eta P planokoa den zuzenaren ekuazioa.Ebazpena :a) P-ri buruz paraleloak izateagatik, bere ekuazioa 2x-y+2z+d=0
izango da.Esferaren zentroa C(1,0,0) da eta bere erradioa r = 5.C-tik plano ukitzaile horietarako distantziak 5 balio behar du, hori baita erradioaren luzera ; beraz: ~(4+ 1 +4)
Balio absolutua kendu eta bi ekuazioak ebatzita, hau lortzen da : d
= 13 edo d = -17. Beraz, honako hauek dira emaitzak : 2x - y + 2z +
13 = 0 eta 2x - y + 2z -17 = 0b) Zentrotik pasaz P planoaren perpendikularra den zuzena,
honako hau da :
~(4+ 1 +4)
Balio absolutua kendu eta bi ekuazioak ebatzita, hau lortzen da : d
= 13 edo d = -17. Beraz, honako hauek dira emaitzak : 2x - y + 2z +
13 = 0 eta 2x - y + 2z -17 = 0b) Zentrotik pasaz P planoaren perpendikularra den zuzena,
honako hau da :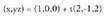 P planoarekin duen ebakidura kalkulatzeko, planoaren ekuazioan ordezkatu eta hau aterazen da : 2(1+2t) - (-t) +2(2t) + 7 = 0. Emaitza t = -1 da eta planoak esferan eragiten duen ebakidura zirkuluaren zentroa,
P planoarekin duen ebakidura kalkulatzeko, planoaren ekuazioan ordezkatu eta hau aterazen da : 2(1+2t) - (-t) +2(2t) + 7 = 0. Emaitza t = -1 da eta planoak esferan eragiten duen ebakidura zirkuluaren zentroa,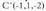 da.C-tik
da.C-tik - rako distantzia,
- rako distantzia,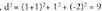 da eta esferaren erradioa 5 da ; beraz :
da eta esferaren erradioa 5 da ; beraz : eta erradioa 4 da.c) Erradiorik txikiena duen esfera berriz,
eta erradioa 4 da.c) Erradiorik txikiena duen esfera berriz, zentrotzat eta erradioa 4 dituena izango da, hau da :
zentrotzat eta erradioa 4 dituena izango da, hau da :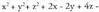 d) A puntuan ukitzaile den zuzena, esferarekiko A-n ukitzaile den planoan dago. Bestalde, P planoan ere badago ; beraz, bere norabide bektorea, P planoaren bektore perpendikularrari buruz zuta izangodu P planoan ere badagoelako, baina baita A-n amaitzen den erradioaren arabera doan
d) A puntuan ukitzaile den zuzena, esferarekiko A-n ukitzaile den planoan dago. Bestalde, P planoan ere badago ; beraz, bere norabide bektorea, P planoaren bektore perpendikularrari buruz zuta izangodu P planoan ere badagoelako, baina baita A-n amaitzen den erradioaren arabera doan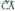 bektoreari buruz ere, ukitzaile delako.Dagoeneko ezaguna da zuzenaren A(-11/3, -5/3, -2/3) puntua.
bektoreari buruz ere, ukitzaile delako.Dagoeneko ezaguna da zuzenaren A(-11/3, -5/3, -2/3) puntua.
Zuzenaren norabide bektorea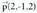 bektoreari buruz eta
bektoreari buruz eta erradioari buruz zuta da; beraz, norabide bektorea, beste bi bektore horien biderkadura bektoriala da :
erradioari buruz zuta da; beraz, norabide bektorea, beste bi bektore horien biderkadura bektoriala da :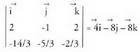 Beraz, zuzena, honako hau izango da :
Beraz, zuzena, honako hau izango da :
- Ariketak
38. Zehatz ezazu r zuzenak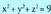 ekuaziodun esferarekin duen ebakidura, r zuzenaren ekuazioak ondorengoak idren kasuetan :
ekuaziodun esferarekin duen ebakidura, r zuzenaren ekuazioak ondorengoak idren kasuetan :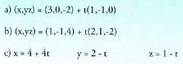 39. a) Aztertu
39. a) Aztertu
- Beste ariketa batzuek
1. Ondorengo ekuaziodun esferak ematen dira : a) Kalkula ezazu horietako bakoitzaren zentroa eta erradioa
eta bien zentroak elkartzen dituen zuzenaren ekuazioa.b) Froga ezazu bi esferak ebakitzaileak direla (elkar ebakitzen
dutela) eta aurkitu puntu komunetatik igarotzen den
planoaren ekuazioa.c) Froga ezazu plano hori zentroak elkartzen dituen zuzenaren
perpendikularra dela.d) Kalkulatu bi esferen ebakidura den zirkunferentziaren
zentroa eta erradioa :Ebazpenak :a) x,y,z ezezagunen monomioen eta zentroaren koordenatuen
arteko koefizienteen erlazioak hauek dira :
a) Kalkula ezazu horietako bakoitzaren zentroa eta erradioa
eta bien zentroak elkartzen dituen zuzenaren ekuazioa.b) Froga ezazu bi esferak ebakitzaileak direla (elkar ebakitzen
dutela) eta aurkitu puntu komunetatik igarotzen den
planoaren ekuazioa.c) Froga ezazu plano hori zentroak elkartzen dituen zuzenaren
perpendikularra dela.d) Kalkulatu bi esferen ebakidura den zirkunferentziaren
zentroa eta erradioa :Ebazpenak :a) x,y,z ezezagunen monomioen eta zentroaren koordenatuen
arteko koefizienteen erlazioak hauek dira : S esferarentzat berriz :
S esferarentzat berriz : Hortik ateratzen da C(1,2,1) duela zentroa, eta erradioa
r = 3 duela.Q-ren kasuan berriz :
Hortik ateratzen da C(1,2,1) duela zentroa, eta erradioa
r = 3 duela.Q-ren kasuan berriz :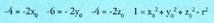 Hortik ateratzen da
Hortik ateratzen da duela zentroa, eta erradioa
duela zentroa, eta erradioa duela.Zentroak elkartzen dituen zuzenak norabide bektore hau du :
duela.Zentroak elkartzen dituen zuzenak norabide bektore hau du : eta C-tik igarotzen da ; beraz :
eta C-tik igarotzen da ; beraz : b) Zentroen arteko distantzia berriz :
b) Zentroen arteko distantzia berriz : eta erradioen batura
eta erradioen batura da, beren kendura
da, beren kendura dela. Zentroen arteko distantzia, bi balio horien artean dago ; beraz, elkar ebakitzen dute.Zein planoren arabera elkar ebakitzen duten jakiteko, bi
ekuazioen kenketa egingo dugu :
dela. Zentroen arteko distantzia, bi balio horien artean dago ; beraz, elkar ebakitzen dute.Zein planoren arabera elkar ebakitzen duten jakiteko, bi
ekuazioen kenketa egingo dugu :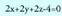 Sinplifikatuta :
Sinplifikatuta : c)
c) bektorea (1,1,1) da eta aurkitutako planoaren bektore perpendikularra,
bektorea (1,1,1) da eta aurkitutako planoaren bektore perpendikularra, koefizienteek eratua da ; beraz, planoa, zentroak elkartzen dituen zuzenari buruz zuta da.d) Zentroa berriz, zentroak elkartzen dituen planoaren eta
zuzenaren arteko ebakidura da :
koefizienteek eratua da ; beraz, planoa, zentroak elkartzen dituen zuzenari buruz zuta da.d) Zentroa berriz, zentroak elkartzen dituen planoaren eta
zuzenaren arteko ebakidura da :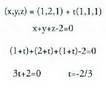 Beraz, zentroa D(1/3, 4/3, 1/3) izango da.Erradioa jakiteko berriz, planoaren eta C zentrodun esferaren arteko ebakidura hartzen da kontuan :
Beraz, zentroa D(1/3, 4/3, 1/3) izango da.Erradioa jakiteko berriz, planoaren eta C zentrodun esferaren arteko ebakidura hartzen da kontuan : C(1,2, l) zentrodun eta R = 3 erradiodun S esfera hartuta :
C(1,2, l) zentrodun eta R = 3 erradiodun S esfera hartuta :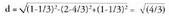 Orduan,
Orduan, 2.A. Erreferentzi sistema ortonormaleko hiru dimentsiotako espazio euklidear batean,
2.A. Erreferentzi sistema ortonormaleko hiru dimentsiotako espazio euklidear batean, puntuak ditugu.i) Kalkulatu A, B eta C puntuak barne dituen planoaren
ekuazioa.ii) Kalkulatu A eta B puntuetatik igarotzen den zuzenaren
ekuazioa.iii) Kalkulatu jatorri puntutik r zuzenerako distantzia.B.
puntuak ditugu.i) Kalkulatu A, B eta C puntuak barne dituen planoaren
ekuazioa.ii) Kalkulatu A eta B puntuetatik igarotzen den zuzenaren
ekuazioa.iii) Kalkulatu jatorri puntutik r zuzenerako distantzia.B. eta D(O,O,O) puntuak erpintzat dituen ABCD tetraedroa emanda :i) Egiaztatu AB, AC eta AD ertzek edo aldeek luzera berdina
dutela.ii) Egiaztatu ABC eta ABD planoek eratzen duten angelua
eta ABC eta ACD planoek eratzen dutena berdinak direla.C. Gauza jakina da ABCD tetraedroak ertzak edo aldeak
eta angeluak berdinak dituela.i) Kalkulatu tetraedroari zirkunskribatutako esferaren
zentroaren koordenatuak.ii) Kalkulatu tetraedroari zirkunskribatutako esfera
horren erradioa eta ekuazioa.iii) Egiaztatu zirkunskribatutako esferaren diametraoren
karratua tetraedroaren aldearen karratua halako bat eta erdi
dela. (Euklides, (K.a. 111. mendea) Elementuak deituriko
XIII. liburuko 13. proposamena)Ebazpena:
A. i )
eta D(O,O,O) puntuak erpintzat dituen ABCD tetraedroa emanda :i) Egiaztatu AB, AC eta AD ertzek edo aldeek luzera berdina
dutela.ii) Egiaztatu ABC eta ABD planoek eratzen duten angelua
eta ABC eta ACD planoek eratzen dutena berdinak direla.C. Gauza jakina da ABCD tetraedroak ertzak edo aldeak
eta angeluak berdinak dituela.i) Kalkulatu tetraedroari zirkunskribatutako esferaren
zentroaren koordenatuak.ii) Kalkulatu tetraedroari zirkunskribatutako esfera
horren erradioa eta ekuazioa.iii) Egiaztatu zirkunskribatutako esferaren diametraoren
karratua tetraedroaren aldearen karratua halako bat eta erdi
dela. (Euklides, (K.a. 111. mendea) Elementuak deituriko
XIII. liburuko 13. proposamena)Ebazpena:
A. i )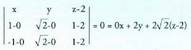 hau da :
hau da :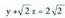 ii) A eta B elkartzen dituen bektorea :
ii) A eta B elkartzen dituen bektorea : Ekuazioa hau da :
Ekuazioa hau da : iii) Jatorri puntutik igarotzen den aurreko zuzenarekiko plano normal edo perpendikularraren ekuazioa,
iii) Jatorri puntutik igarotzen den aurreko zuzenarekiko plano normal edo perpendikularraren ekuazioa, da, izan ere, planoaren perpendikularra den bektoreak, ezezagunen koefizienteen berdinak baititu.Planoaren eta zuzenaren arteko ebaki puntua, planoaren
ekuazioan zuzenaren y eta z koordenatuak x-en arabera
ordezkatuz aurkitzen da.
da, izan ere, planoaren perpendikularra den bektoreak, ezezagunen koefizienteen berdinak baititu.Planoaren eta zuzenaren arteko ebaki puntua, planoaren
ekuazioan zuzenaren y eta z koordenatuak x-en arabera
ordezkatuz aurkitzen da. Beraz, ebaki puntua hau da :
Beraz, ebaki puntua hau da :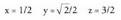 eta kalkulatu nahi den distantzia :
eta kalkulatu nahi den distantzia :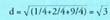 B. i) AB = AC = AD = 2ii) ABC planoaren ekuazioa hau da :
B. i) AB = AC = AD = 2ii) ABC planoaren ekuazioa hau da :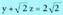 ABD planoarentzat
ABD planoarentzat hau da,
hau da, ACD planoarentzat
ACD planoarentzat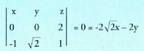 hau da,
hau da,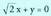 eta ABC eta ABD arteko angelua hau da :
eta ABC eta ABD arteko angelua hau da : ABC eta ACD artekoa berriz:
ABC eta ACD artekoa berriz: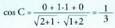 Beraz,
Beraz, C i) AD-ren plano erdibitzailea honako hau da : z = 1AB-ren plano erdibitzailea :
C i) AD-ren plano erdibitzailea honako hau da : z = 1AB-ren plano erdibitzailea :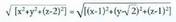 eta sinplifikatuta honela gelditzen da :
eta sinplifikatuta honela gelditzen da : BC-ren plano erdibitzailea x = 0 da.Erdibitzaileen arteko ebaki-puntua zirkunskribatutako esferaren zentroa da
BC-ren plano erdibitzailea x = 0 da.Erdibitzaileen arteko ebaki-puntua zirkunskribatutako esferaren zentroa da ii) Erradioa berriz,
ii) Erradioa berriz, eta zirkunferentziaren ekuazioa :
eta zirkunferentziaren ekuazioa : iii) Ertzaren edo aldearen luzera 2 da (B i) kasuan aurkitua) erradioa
iii) Ertzaren edo aldearen luzera 2 da (B i) kasuan aurkitua) erradioa da ; beraz, diametroa,
da ; beraz, diametroa,
Emaitzak:
1. a) i-j+k b) (-1,0,1)2. a) 1 b) 23. a) (4,4,4) b) (2,3,0), (3,4,1),(4,5,2)4. S(5,3,-4)5. S(-x, -y, -z)6. Bektore ekuazioa : (x,y,z) = (-1,-1,0) + t(1,2,1)Parametro ekuazioak : Ekuazio jarraia : (x+1)/1 = (y+1)/2 = z/17. Bektore ekuazioa: (x,y,z) = (1,2,1) + t(1,1,-1)Parametro ekuazioak :
Ekuazio jarraia : (x+1)/1 = (y+1)/2 = z/17. Bektore ekuazioa: (x,y,z) = (1,2,1) + t(1,1,-1)Parametro ekuazioak : Ekuazio jarraia : (x-1)/1 = (y-2)/1 = (z-1)/18. Bai, puntua zuzenekoa da, t = 2 hartuta.9. Ez, puntua ez da zuzenekoa,
Ekuazio jarraia : (x-1)/1 = (y-2)/1 = (z-1)/18. Bai, puntua zuzenekoa da, t = 2 hartuta.9. Ez, puntua ez da zuzenekoa, 10. P(1,-2,3) puntuan ebakitzen dute elkar.11. Hiru norabide bektoreak linealki askeak dira. Hiru zuzenek
puntu batean elkar ebakitzen dutela frogatzeko, bi zuzenen arteko
ebaki puntua aurkitzen da, eta hirugarren zuzena handik igarotzen
den ala ez egiaztatzen da. Puntu komuna P(0,2,2) da.12. x/3 = y/2 = z13. Emaitza : (x,y,z) _ (1,1,1) + t(2,1,0) + s(1,1,2)Parametro ekuazioa :
10. P(1,-2,3) puntuan ebakitzen dute elkar.11. Hiru norabide bektoreak linealki askeak dira. Hiru zuzenek
puntu batean elkar ebakitzen dutela frogatzeko, bi zuzenen arteko
ebaki puntua aurkitzen da, eta hirugarren zuzena handik igarotzen
den ala ez egiaztatzen da. Puntu komuna P(0,2,2) da.12. x/3 = y/2 = z13. Emaitza : (x,y,z) _ (1,1,1) + t(2,1,0) + s(1,1,2)Parametro ekuazioa : Ekuazio orokorra : 2x - 4y + z + 1 = 014. 13. ariketako emaitza berberak.15. 13. ariketako emaitza berberak.16. a) Ez b) Bai.17. a) Elkar ebakitzen dute b) Paraleloak dira c) Bat datoz.18. 3x - 4y + 2z = 019. (x,y,z) = (0,2,1)+ t(2,-3,1)20. a) Paraleloakb) Ebakitzaileak21.a)900 b) 54° 44' 48"21.a)900 b) 54° 44' 48"22.
Ekuazio orokorra : 2x - 4y + z + 1 = 014. 13. ariketako emaitza berberak.15. 13. ariketako emaitza berberak.16. a) Ez b) Bai.17. a) Elkar ebakitzen dute b) Paraleloak dira c) Bat datoz.18. 3x - 4y + 2z = 019. (x,y,z) = (0,2,1)+ t(2,-3,1)20. a) Paraleloakb) Ebakitzaileak21.a)900 b) 54° 44' 48"21.a)900 b) 54° 44' 48"22.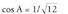 Emaitza :
Emaitza : 23. Perpendikularrak dira, 90°24. (x,y,z) = (1,1,-2) + t(1,-3,2)25. 2x + 2y + 3z - 4 = 026. d = 227.
23. Perpendikularrak dira, 90°24. (x,y,z) = (1,1,-2) + t(1,-3,2)25. 2x + 2y + 3z - 4 = 026. d = 227.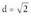 28.
28.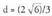 29. d = 4/330. B = 2/33 1. a) proiekzioa
29. d = 4/330. B = 2/33 1. a) proiekzioa inserted textb) proiekzioa
inserted textb) proiekzioa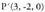 eta simetrikoa S(5,-3,1)32. y+z+1=033. 2x+l ly+5z = 0, 7x+y-5z+15 = 034.
eta simetrikoa S(5,-3,1)32. y+z+1=033. 2x+l ly+5z = 0, 7x+y-5z+15 = 034.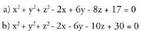 35. a) Ez da esfera b) Bai, C(-1,2,1) zentrotzat eta
35. a) Ez da esfera b) Bai, C(-1,2,1) zentrotzat eta erradioa duena e) Ez da.36.
erradioa duena e) Ez da.36.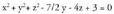 37. A,C eta D puntuak barnekoak dira, B eta E kanpokoak eta F
eta G esfera azalekoak.38. a) (2,1,-2), (1,2,-2) b) (-1,-2,-2) c) kanpokoa.39. a) (0,0,0) zentrotzat eta erradioa 3 duten zirkulu handienak
planoetako bakoitzaren arabera.b) (-1/3, -1/3, -1/3) zentroa eta
37. A,C eta D puntuak barnekoak dira, B eta E kanpokoak eta F
eta G esfera azalekoak.38. a) (2,1,-2), (1,2,-2) b) (-1,-2,-2) c) kanpokoa.39. a) (0,0,0) zentrotzat eta erradioa 3 duten zirkulu handienak
planoetako bakoitzaren arabera.b) (-1/3, -1/3, -1/3) zentroa eta