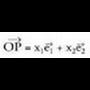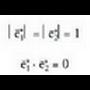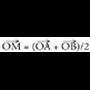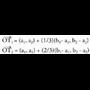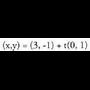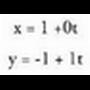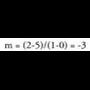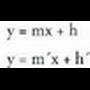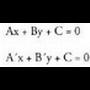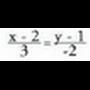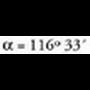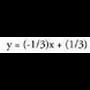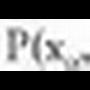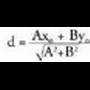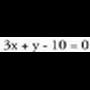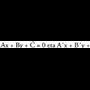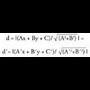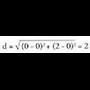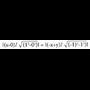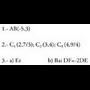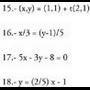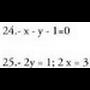Matematika»Geometria
Planoa Geometria Analitikoan
Bektore espazioaren egitura, geometrian erabiltzen da, baina baita ekuazioen ebazpenean, funtzioen teorian eta matematikako beste eremu batzuetan ere. Metodoak antzekoak diren arren, erabilitzen diren bektore espazioaren dimentsioak desberdinak dira erabilpen mota batetik bestera. Geometrian, dimentsio bakarreko bektore espazioarekin erlazionatzen da zuzena, planoa berriz bi dimentsiokoarekin eta espazioa hirukoarekin. Lau dimentsio edo gehiagoko espazioaren senezko geometria ikuspegidun interpretazioak, bistakoa ez dirudien arren, egitura horrek aukera ematen du plano edo espazio arruntean aurkitutako edozein dimentsio kopuruko geometria espazioak orokortzeko. Kapitulu honetan, bi dimentsioko bektore espazioaren laguntzaz, planoko ariketak eta arazoak nola ebazten diren aztertuko dugu.
I. Erreferentzia sistema. Kokapen bektorea eta puntuaren koordenatuak.
Jatorri puntu deritzon O puntuaz eta bektore espazioko oinarri diren eta
eta bektore bikote batek eratutako multzoari, planoaren erreferentzia sistema deritzo.
bektore bikote batek eratutako multzoari, planoaren erreferentzia sistema deritzo.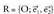 erreferentzia sistema hori emanik, planoko P puntu bakoitzari bektore bat dagokio, puntuaren kokapen bektor e deitua, eta bektore hori jatorri puntua P puntuarekin lotzen duen
erreferentzia sistema hori emanik, planoko P puntu bakoitzari bektore bat dagokio, puntuaren kokapen bektor e deitua, eta bektore hori jatorri puntua P puntuarekin lotzen duen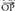 bektorea da. Emandako oinarrian, orokorki ondoko hau betetzen da :
bektorea da. Emandako oinarrian, orokorki ondoko hau betetzen da :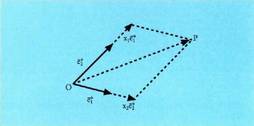 Era horretan, erreferentzia bat izanda, planoko puntu bakoitzari, alde batetik bektore aske bat egoki arazten zaio, ordezkari
Era horretan, erreferentzia bat izanda, planoko puntu bakoitzari, alde batetik bektore aske bat egoki arazten zaio, ordezkari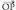 duena, eta bestalde, zenbaki bikote bat, emandako oinarrian bere koordenatu diren
duena, eta bestalde, zenbaki bikote bat, emandako oinarrian bere koordenatu diren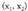 alegia.Geometria analitikoan, erreferentzia sistema ona edukitzeak, izugarri laguntzen du problemak eta ariketak ebazten, izan ere, geroagoko aljebrako kalkuluak asko sinplifika baititzake. Bektoreek bateko modulua duten oinarriari, ortogonala deitzen zaio eta elkarri buruz zutak baldin badira berriz, normala. Oinarririk erabiliena, ortonormala da, hau da, bektoreek bateko oinarria dutena eta elkarri buruz zutak direna,
alegia.Geometria analitikoan, erreferentzia sistema ona edukitzeak, izugarri laguntzen du problemak eta ariketak ebazten, izan ere, geroagoko aljebrako kalkuluak asko sinplifika baititzake. Bektoreek bateko modulua duten oinarriari, ortogonala deitzen zaio eta elkarri buruz zutak baldin badira berriz, normala. Oinarririk erabiliena, ortonormala da, hau da, bektoreek bateko oinarria dutena eta elkarri buruz zutak direna,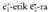 joateko biraketa norantza positiboa edota erloju orratzen aurkakoa duena.
joateko biraketa norantza positiboa edota erloju orratzen aurkakoa duena.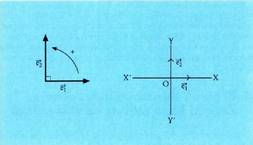 Jatorri puntutik igaroz oinarriko bektoreetako baten norabidea
duen zuzenari koordenatu ardatz deitzen zaio.Edozein erreferentzia sistemak ere, planoko puntu bakoitza, bere
koordenatuak diren bi zenbaki errealekin erlazionatzen du. Puntuaren
koordenatuak edota puntuari dagokion OA kokapen bektorea
emanda, A puntua erabat zehaztuta dago.Oinarriko bektoreen koordenatuak, (1,0) eta (0,1) dira eta oinarria ortonormala baldin bada, bi bektoreren
Jatorri puntutik igaroz oinarriko bektoreetako baten norabidea
duen zuzenari koordenatu ardatz deitzen zaio.Edozein erreferentzia sistemak ere, planoko puntu bakoitza, bere
koordenatuak diren bi zenbaki errealekin erlazionatzen du. Puntuaren
koordenatuak edota puntuari dagokion OA kokapen bektorea
emanda, A puntua erabat zehaztuta dago.Oinarriko bektoreen koordenatuak, (1,0) eta (0,1) dira eta oinarria ortonormala baldin bada, bi bektoreren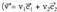 eta
eta biderkadura eskalarraren adierazpena honako hau da :
biderkadura eskalarraren adierazpena honako hau da :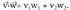 Adibidez,
Adibidez,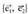 oinarri ortonormala badugu eta OA(1,2) eta OB(3,4) bektoreak, biderkadura eskalarra, ondorengoa izango litzateke :
oinarri ortonormala badugu eta OA(1,2) eta OB(3,4) bektoreak, biderkadura eskalarra, ondorengoa izango litzateke :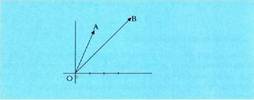 Koordenatu horiek beste oinarri bati balegozkio,
Koordenatu horiek beste oinarri bati balegozkio,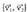 oinarriari adibidez, eta oinarri berri honetako bektoreak 2 modul udunak balira eta elkarren artean 60°-ko angelua eratuko balute,
oinarriari adibidez, eta oinarri berri honetako bektoreak 2 modul udunak balira eta elkarren artean 60°-ko angelua eratuko balute,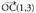 eta
eta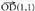 bektoreen biderkadura ondoko hau izango litzateke :
bektoreen biderkadura ondoko hau izango litzateke :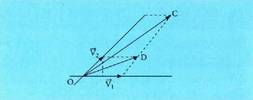
I I. Bi puntu elkartzen dituen bektorea.
Zuzenki baten zatiketa hainbat zatitan.
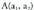 eta
eta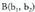 puntuak emanik,
puntuak emanik,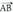 bektorea lor daiteke ondorengoa kontuan hartuta :
bektorea lor daiteke ondorengoa kontuan hartuta :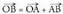 Hau da :
Hau da :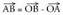 Beraz, bere koordenatuak, hauek izango dira :
Beraz, bere koordenatuak, hauek izango dira :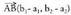 Adibidez,
Adibidez,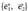 oinarrian, A(2,1) eta B(3,0) koordenatuak dituzten puntuak lotzen dituen bektorea, (1, -1) bektorea da.
oinarrian, A(2,1) eta B(3,0) koordenatuak dituzten puntuak lotzen dituen bektorea, (1, -1) bektorea da.
Zuzenki baten erdiko puntua.
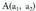 eta
eta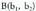 puntuak emanik, biak elkartzen dituen zuzenkiaren erdik puntua jakitea, bere
puntuak emanik, biak elkartzen dituen zuzenkiaren erdik puntua jakitea, bere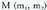 koordenatuak edota bere
koordenatuak edota bere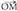 kokapen bektorea jakitea da. Bi bektoreren batura definitzeko geroago ikusiko den paralelogramoaren araua kontuan hartuta, AB zuzenkiaren erdiko puntua,
kokapen bektorea jakitea da. Bi bektoreren batura definitzeko geroago ikusiko den paralelogramoaren araua kontuan hartuta, AB zuzenkiaren erdiko puntua,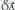 eta
eta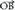 batzeko eratutako paralelogramoaren erdi erdian aurkitzen da, beraz :
batzeko eratutako paralelogramoaren erdi erdian aurkitzen da, beraz :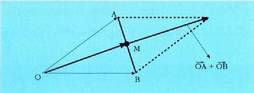 Koordenatuetan jarrita :
Koordenatuetan jarrita :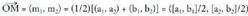 Adibidez, A(1,2) eta B(3,4) puntuen erdiko puntua :
Adibidez, A(1,2) eta B(3,4) puntuen erdiko puntua :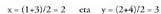 Zuzenki bat hiru zatitan, lautan edo gehiagotan zatitzen duten puntuak aurkitu nahi badira, aurreko metodoa ezin daiteke erabili.
Zuzenki bat hiru zatitan, lautan edo gehiagotan zatitzen duten puntuak aurkitu nahi badira, aurreko metodoa ezin daiteke erabili.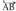 zuzenkia hiru zati berdinetan zatitu nahi baldin bada,
zuzenkia hiru zati berdinetan zatitu nahi baldin bada,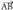 bektorea aurkitu eta hiru zatitan zatitzen da ondoko bektore hauek kalkulatuz :
bektorea aurkitu eta hiru zatitan zatitzen da ondoko bektore hauek kalkulatuz :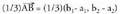 eta
eta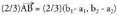 Zuzenkia hiru zati berdinetan zatitzen duten kokapen bektoreak edota
Zuzenkia hiru zati berdinetan zatitzen duten kokapen bektoreak edota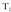 eta
eta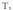 puntuen koordenatuak jakiteko, honela egiten da :
puntuen koordenatuak jakiteko, honela egiten da :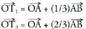 Koordenatutan jarrita :
Koordenatutan jarrita :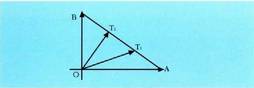 Adibidez, zatitu hiru zatitan A(3,1) eta B(6,3) muturrak dituen
zuzenkia :
Adibidez, zatitu hiru zatitan A(3,1) eta B(6,3) muturrak dituen
zuzenkia :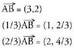 Beraz,
Beraz,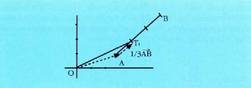 AB zuzenkia k zati berdinetan zatitu nahi baldin bada, erraz orokortzen
da aurreko formula. AB zuzenkia k zatitan zatitzen duten k- 1
puntuak, ondoko adierazpenean m-ri balioak emanez lortzen dira :
AB zuzenkia k zati berdinetan zatitu nahi baldin bada, erraz orokortzen
da aurreko formula. AB zuzenkia k zatitan zatitzen duten k- 1
puntuak, ondoko adierazpenean m-ri balioak emanez lortzen dira :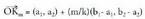 k = m denean, adierazpen horrek
k = m denean, adierazpen horrek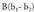
Hiru puntu lerrokatu.
Hiru puntu, edozein, ordenatuta baldin badaude, lehenengoa eta
bigarrena elkartzen dituen bektoreak, eskalar batez (zenbaki batez)
biderkatuta, lehenengoa hirugarrenarekin elkartzen duen bektorea
eman behar du.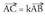 Baina,
Baina,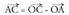 eta
eta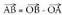 direnez,koordenatuetan, ondorengoa ateratzen da :
direnez,koordenatuetan, ondorengoa ateratzen da :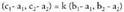 eta hortik, zera ateratzen da, alegia, A,B eta C lerrokatuta daudela
ondorengoa betez gero :
eta hortik, zera ateratzen da, alegia, A,B eta C lerrokatuta daudela
ondorengoa betez gero :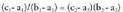 Adibidez, A(1,3), B(5,1) eta C(-1,-1) puntuak lerrokatuta dauden
ala ez jakin nahi baldin badugu, honako hau egiten da :
Adibidez, A(1,3), B(5,1) eta C(-1,-1) puntuak lerrokatuta dauden
ala ez jakin nahi baldin badugu, honako hau egiten da :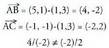 Beraz, ez daude lerrokatuta.
Beraz, ez daude lerrokatuta.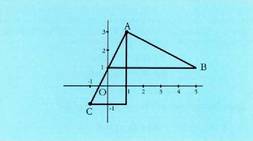 A(4,1), B(1,3) eta C(-2,5) puntuak lerrokatuta dauden ala ez
jakin nahi baldin badugu :
A(4,1), B(1,3) eta C(-2,5) puntuak lerrokatuta dauden ala ez
jakin nahi baldin badugu :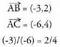 Beraz, lerrokatuta daude.
Beraz, lerrokatuta daude.
0 Ariketak
1. Aurki itzazu A(3,-1) eta B(-2,2) puntuak elkartzen dituen bektorearen koordenatuak.2. Kalkula itzazu A(1,3) eta B(5,5) puntuak muturtzat
dituen zuzenkia lau zati berdinetan zatitzen dituzten puntuen
koordenatuak.3. Esazu ea ondorengo puntuak lerrokatuta dauden :
bektorearen koordenatuak.2. Kalkula itzazu A(1,3) eta B(5,5) puntuak muturtzat
dituen zuzenkia lau zati berdinetan zatitzen dituzten puntuen
koordenatuak.3. Esazu ea ondorengo puntuak lerrokatuta dauden :
I I I. Zuzenaren ekuazioa.
Emandako A eta B puntuekin lerrokatuta dagoen C puntuak,
ondorengoa betetzen du :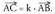 Eta alderantziz, berdintza hori betetzen duten X puntuak, A eta B
puntuekin lerrokatuta daude eta ondorengo ekuazioa betetzen
dute :
Eta alderantziz, berdintza hori betetzen duten X puntuak, A eta B
puntuekin lerrokatuta daude eta ondorengo ekuazioa betetzen
dute :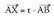 Ekuazio honek, hain zuzen ere, zuzenaren ekuazioan ematen den
moduetako lehenengoa ematera garamatza :
Ekuazio honek, hain zuzen ere, zuzenaren ekuazioan ematen den
moduetako lehenengoa ematera garamatza :
Bektore ekuazioa.
Zuzen baten A puntu bat eta norabidea baldin badakizkigu, zuzena
zeharo zehaztuta dago. Geometria analitikoan, norabidea emateko
modurik errazena, norabide hori duen bektorea ematea da. D
bektore horri zuzenaren norabide bektore deritzo.Demagun puntua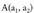 dela eta norabidea
dela eta norabidea bektoreak etmaten duela. P(x,y) puntua zuzenekoa bada,
bektoreak etmaten duela. P(x,y) puntua zuzenekoa bada,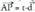 .dizan beharko du, hots,
.dizan beharko du, hots,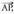 norabide bektorearen norabidean egon behar du.
norabide bektorearen norabidean egon behar du.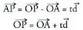 Ekuazio hori, edozein oinarritan hartuta, hau da :
Ekuazio hori, edozein oinarritan hartuta, hau da :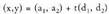 Forma edo eite horri, zuzenaren bektore ekuazio deitzen zaio.Adibidez, A(1,2) puntutik igaro eta d(-1,3) norabide bektoretzat
duen zuzenaren ekuazioa hau da :
Forma edo eite horri, zuzenaren bektore ekuazio deitzen zaio.Adibidez, A(1,2) puntutik igaro eta d(-1,3) norabide bektoretzat
duen zuzenaren ekuazioa hau da :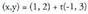 B(-3, l) puntutik igaro eta e z oinarri bektorearekiko paraleloa den
zuzenak bektore ekuazio hau du :
B(-3, l) puntutik igaro eta e z oinarri bektorearekiko paraleloa den
zuzenak bektore ekuazio hau du :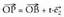 Hau da :
Hau da :
Parametro ekuazioa.
Aurreko bektore ekuazioa, oinarriaren bi bektoreen arabera bi
ekuazio eskalar desberdinetan deskonposatzen bada, hau ateratzen
da: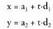 Ekuazio horiei parametro ekuazio deritze, izan ere, bistan uzten
baitute puntu baten koordenatuen balioak t parametroak dituen
balioen baitan daudela. Balio horri parametro deitzen zaio eta hautazko
balioak eman diezazkiokeen finkatu gabeko kopurua izan ohi
da. Parametroa ez da ezezagun bat, zuzenaren ekuazioa betetzen
duten puntu infinituak multzoan adierazteko modua baizik.Adibidez, lehen bektore ekuazio bidez ikusitako A(1,2) puntutik igarotzen den eta
Ekuazio horiei parametro ekuazio deritze, izan ere, bistan uzten
baitute puntu baten koordenatuen balioak t parametroak dituen
balioen baitan daudela. Balio horri parametro deitzen zaio eta hautazko
balioak eman diezazkiokeen finkatu gabeko kopurua izan ohi
da. Parametroa ez da ezezagun bat, zuzenaren ekuazioa betetzen
duten puntu infinituak multzoan adierazteko modua baizik.Adibidez, lehen bektore ekuazio bidez ikusitako A(1,2) puntutik igarotzen den eta norabide bektorea duen zuzenaren ekuazioak, hau du bektore ekuazioa :
norabide bektorea duen zuzenaren ekuazioak, hau du bektore ekuazioa :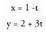 B(1,-1) puntutik igaro eta e2 oinarriaren bektorearekiko paraleloa
den zuzenak parametro ekuazio hau du :
B(1,-1) puntutik igaro eta e2 oinarriaren bektorearekiko paraleloa
den zuzenak parametro ekuazio hau du :
Ekuazio jarraia.
Puntu desberdinak parametro bati balioak emanez lortu nahi ez
badira eta nahiago baldin bada zuzenaren puntuek bete behar duten
baldintzaren bat edukitzea, parametroa deuseztatu eta x eta y ezezagunak
dituen ekuazio bakarra ateratzen da : Bi ekuazioetan t-ren balioak berdinduz, ondokoa ateratzen da :
Bi ekuazioetan t-ren balioak berdinduz, ondokoa ateratzen da :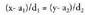 Eta horri zuzenaren ekuazio deritzo.Adibidez, A(2,1) puntutik igaro eta
Eta horri zuzenaren ekuazio deritzo.Adibidez, A(2,1) puntutik igaro eta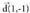 norabide-bektoreduen zuzenaren ekuazio jarraia hau da :
norabide-bektoreduen zuzenaren ekuazio jarraia hau da :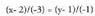 B(3,-2) puntutik igaro eta
B(3,-2) puntutik igaro eta norabide-bektoretzat duen zuzenarena berriz :
norabide-bektoretzat duen zuzenarena berriz :
Ekuazio inplizitua.
Ekuazio jarraia sinplifikatuz gero, x eta y gaiak gai askearen ondoan
eta alde berean jarrita, dena zerori berdinduta, ekuazio inplizitua
ateratzen da. Hori noski, zuzenaren ekuazioa lehen mailako bi ezezaguneko
ekuazioek duten itxuraren arabera idaztea bezala da.
Hauek dira horretarako eman beharreko urratsak :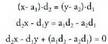 Zuzen baten ekuazioaren itxura orokorra hau da:
Zuzen baten ekuazioaren itxura orokorra hau da: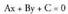 Aljebrako ekuazioen itxura orokor berbera izatea, horixe da ekuazio
itxura horren abantaila. Eragozpena berriz, hor norabide bektorea
lortzea ez dela hain erraza. Eragiketarik egin gabe norabide bektorea
lortu nahi baldin bada, aurreko kalkuluetatik eta x eta y ren
koefizienteak nola atera diren ikusita, norabide bektorea honako
hau da : d(-B,A).Adibidez, D(3,1) puntutik igaro eta
Aljebrako ekuazioen itxura orokor berbera izatea, horixe da ekuazio
itxura horren abantaila. Eragozpena berriz, hor norabide bektorea
lortzea ez dela hain erraza. Eragiketarik egin gabe norabide bektorea
lortu nahi baldin bada, aurreko kalkuluetatik eta x eta y ren
koefizienteak nola atera diren ikusita, norabide bektorea honako
hau da : d(-B,A).Adibidez, D(3,1) puntutik igaro eta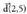 norabide bektoretzat duen zuzenaren ekuazio inplizitua hau izango da :
norabide bektoretzat duen zuzenaren ekuazio inplizitua hau izango da : Eragiketak eginda :
Eragiketak eginda :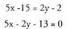 Norabide bektorearen osagaietatik eta koefizienteen arteko erlaziotik
nahiz 5x -2y + C = 0 ekuazio inplizitutik abia daiteke.x = 3 eta y = 1 balioak ekuazioaren emaitza dira, beraz,
Norabide bektorearen osagaietatik eta koefizienteen arteko erlaziotik
nahiz 5x -2y + C = 0 ekuazio inplizitutik abia daiteke.x = 3 eta y = 1 balioak ekuazioaren emaitza dira, beraz,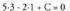 Orduan,C=-13eta emaitza berberera iritsi gara.
Orduan,C=-13eta emaitza berberera iritsi gara.
Ekuazio esplizitua.
Ekuazio bat funtzio baten adierazpen analitiko moduan uler daiteke
. y aldagaia alde batean aske baldin badago, funtzioa esplizituki
edo askatuta emanda dagoela esaten da. Aurreko kasuan ekuazioa
era inplizituan zegoen, izan ere, ekuazio berean x eta y ezezagunak
baitzeuden askatu gabe. y askatuta, zuzenaren ekuazio esplizitua
edo askea ateratzen da :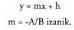 m konstanteari zuzenaren malda deritzo, izan ere, m-k, x unitate
bat handitzen edo txikitzen denean y handitzen edo txikitzen
dena adierazten baitu. Zuzenaren definizioaren arabera, kopuru
hori konstantea da, izan ere, zuzenek ez baitute norabidez aldatzen.
m konstanteari zuzenaren malda deritzo, izan ere, m-k, x unitate
bat handitzen edo txikitzen denean y handitzen edo txikitzen
dena adierazten baitu. Zuzenaren definizioaren arabera, kopuru
hori konstantea da, izan ere, zuzenek ez baitute norabidez aldatzen.
Malda horrek erlazioa du zuzenaren zeihartasunak edo inklinazioak
lehenengo ardatzarekiko edo ardatz horizontal edo x ardatzarekiko
eratzen duen angeluarekin, eta ardatzak ortonormalak badira,
m = tga da, beti ere, a zuzenak x ardatzaren edo abzisa ardatzaren
norantza positiboarekin eratzen duen angelua izanik ; angelu horri,
zuzenaren zeihartasun angelu edo inklinazio angelu deitzen zaio.y = x - 3 ekuazioan adibidez,malda 1 baliokoa duen zuzena da, hau da, x ardatzarekiko zuzenak
duen zeihartasuna 45 °-koa da. y = -2x -2 ekuaziodun zuzenean, a = 116º 33´-koa da.
y = -2x -2 ekuaziodun zuzenean, a = 116º 33´-koa da. Ekuazio esplizitua edo askea da lortzen errazena zuzenaren maldaren balioa jakinez gero. h balioa, x zero egiten duenean y-k duen balioa da eta zuzenak jatorrian duen ordenatua deritzo.
Ekuazio esplizitua edo askea da lortzen errazena zuzenaren maldaren balioa jakinez gero. h balioa, x zero egiten duenean y-k duen balioa da eta zuzenak jatorrian duen ordenatua deritzo.
Ekuazio jarraia, ezin daiteke erabili norabide bektorea ardatzetako batekiko paraleloa denean. Hain zuzen ere, norabide bektorean osagaietakoren bat hutsala baldin bada, ez da bere balioaz zatitzerik izango.
Adibidez, demagun dela. Orduan:
dela. Orduan: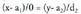 Eta hori aljebra arloan ez da zuzena, izan ere zeroaz ezin baita zatitu. Halere, adierazita uzten da n orabide bektoreak ezagunak izan daitezen, edota
Eta hori aljebra arloan ez da zuzena, izan ere zeroaz ezin baita zatitu. Halere, adierazita uzten da n orabide bektoreak ezagunak izan daitezen, edota , idazten da. d-bigarren osagaia zero bihurtzen bada berriz,
, idazten da. d-bigarren osagaia zero bihurtzen bada berriz,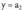 gelditzen da.. = a edota y = b adierazpenak izango lirateke ekuazio esplizituak edo askeak kasu arazotsu eta berezi hauetan. Halere,
gelditzen da.. = a edota y = b adierazpenak izango lirateke ekuazio esplizituak edo askeak kasu arazotsu eta berezi hauetan. Halere, , ez da funtzio baten ekuazioa, beraz, kasu honetan ere, zorrotz hitz eginda, ez litzateke ekuazio eite espliziturik edo askerik izango.
, ez da funtzio baten ekuazioa, beraz, kasu honetan ere, zorrotz hitz eginda, ez litzateke ekuazio eite espliziturik edo askerik izango.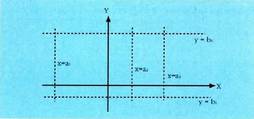
- Ariketak
4. Kalkula ezazu A(2, 1) puntutik igaro eta d(-1,2) norabide bektorea duen zuzenaren ekuazioa, baina ondoko modu desberdin hauetan :
a) bektore ekuazioa
b) parametro ekuazioa
c) ekuazio jarraia
d) ekuazio inplizitua
e) ekuazio esplizitua edo askea.5. Kalkulatu B(1,-1) puntutik igaro eta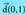 norabide bektorearekiko paraleloa den zuzenaren ekuazioa ondorengo modu hauetan :a) bektore ekuazioa b) parametro ekuazioac) ekuazio jarraia
d) ekuazio inplizituae) ekuazio esplizitua edo askea.6. Kalkula ezazu jatorri puntutik igaroz
norabide bektorearekiko paraleloa den zuzenaren ekuazioa ondorengo modu hauetan :a) bektore ekuazioa b) parametro ekuazioac) ekuazio jarraia
d) ekuazio inplizituae) ekuazio esplizitua edo askea.6. Kalkula ezazu jatorri puntutik igaroz
IV. Zuzenaren eta puntuaren arteko erlazioa.
Puntu bat beti ere zuzen batekoa da bere ekuazioak betetzen baditu
. Hori egiaztatzeko modua ordea, zuzenaren ekuazioa emanda
datorren eraren baitakoa da.Zuzenaren ekuazioa bektore ekuazio moduan edota parametro
ekuazio gisa emanda baldin badago, puntua zuzenekoa izango da
baldin eta t parametroaren balioren batek zuzenaren ekuazioa betetzen
badu edo ekuazioak betetzen baditu. Gainerako moduentzat,
puntua zuzenekoa izango da baldin eta ekuazioko x eta y puntuaren
koordenatu balioez ordezkatzean ekuazioa identitate bihurtzen
bada. Berdintza faltsua edo hobeto esanda, desberdintza ematen
badu, puntua ez da zuzenekoa izango.Adibidez, jakizu P(0,1) puntua honako ekuazio hauek dituen
zuzenekoa den : t = -1 balioak x = 0 ematen duela ikusten da. Bigarren ekuazioan
t = -1 balioaz ordezkatuz, y = 1 ematen du, beraz, P, r zuzenekoa da.
t = -1 balioak x = 0 ematen duela ikusten da. Bigarren ekuazioan
t = -1 balioaz ordezkatuz, y = 1 ematen du, beraz, P, r zuzenekoa da.
Hala ere ordea, Q(1,2) puntua ez da zuzen horretakoa, izan ere, x =
1 balioa, t = -1 /2 ematen baitu parametroarentzat eta balio horrekin
y = 5/2 da eta ez 2, beraz, Q ez dago r zuzenean.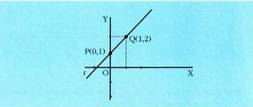 R(3,-2) puntua 2x + y - 4 = 0 ekuaziodun s zuzenekoa den ala ez
jakiteko, x, 3 balioaz ordezkatzen da, eta y, -2 balioaz. Orduan :
2.3+(-2)-4 = 0. Eragiketak eginez, 0 = 0 gelditzen da, beraz, egia da,
eta R puntua s zuzenekoa da. S(2,1) puntua hala den jakiteko, x, 2
balioaz ordezkatuko dugu, eta y, 1 balioaz. Orduan, 2.2+1 -4 = 0
gelditzen da eta 1 = 0 ematen du. Hori ez da egia, beraz, S puntua ez
da s zuzenekoa.Zuzenaren ekuazioa emanda, zuzen horretako puntu bat jakin
nahi baldin bada, nahikoa da parametroari balio bat ematea, bai
bektore ekuazioa dugunean eta baita parametro ekuazioa duguneanere. Ekuazio jarraia, inplizitua edo esplizitua baldin badugu, osagaietako
bati balio bat ematen zaio eta bestearen balioa kalkulatzen
da. Esplizituarentzat beti ere hobe da x-en balioa finkatzea.Adibidez, ondoko ekuazio hau duen zuzeneko puntu bat jakiteko:
R(3,-2) puntua 2x + y - 4 = 0 ekuaziodun s zuzenekoa den ala ez
jakiteko, x, 3 balioaz ordezkatzen da, eta y, -2 balioaz. Orduan :
2.3+(-2)-4 = 0. Eragiketak eginez, 0 = 0 gelditzen da, beraz, egia da,
eta R puntua s zuzenekoa da. S(2,1) puntua hala den jakiteko, x, 2
balioaz ordezkatuko dugu, eta y, 1 balioaz. Orduan, 2.2+1 -4 = 0
gelditzen da eta 1 = 0 ematen du. Hori ez da egia, beraz, S puntua ez
da s zuzenekoa.Zuzenaren ekuazioa emanda, zuzen horretako puntu bat jakin
nahi baldin bada, nahikoa da parametroari balio bat ematea, bai
bektore ekuazioa dugunean eta baita parametro ekuazioa duguneanere. Ekuazio jarraia, inplizitua edo esplizitua baldin badugu, osagaietako
bati balio bat ematen zaio eta bestearen balioa kalkulatzen
da. Esplizituarentzat beti ere hobe da x-en balioa finkatzea.Adibidez, ondoko ekuazio hau duen zuzeneko puntu bat jakiteko: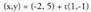
Bi puntutatik igarotzen den zuzena.
Bi puntuk zuzena zehazten dute, beraz, zuzenaren ekuazioa emateko beste modu bat zuzen horretakoak diren bi puntu ematea da.
Bitez , puntu horiek.Bektore ekuazioa, parametro ekuazioa edota ekuazio jarraia lortzeko,
, puntu horiek.Bektore ekuazioa, parametro ekuazioa edota ekuazio jarraia lortzeko,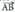 bektorea kalkulatzetik hastea da onena. Bektore hori zuzenaren norabide bektorea da :
bektorea kalkulatzetik hastea da onena. Bektore hori zuzenaren norabide bektorea da : eta orduan horietako edozein zuzena igarotzen den puntutzat
hartzen da. Adibidez, honako bektore ekuazio hau lortuko da :
eta orduan horietako edozein zuzena igarotzen den puntutzat
hartzen da. Adibidez, honako bektore ekuazio hau lortuko da :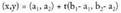 Kalkulatu A(3,1) eta B(2,2) puntuetatik igarotzen den zuzenaren
bektore ekuazioa:
Kalkulatu A(3,1) eta B(2,2) puntuetatik igarotzen den zuzenaren
bektore ekuazioa: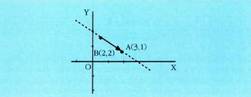 Beraz, parametro ekuazioa :
Beraz, parametro ekuazioa :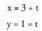 Itxura esplizitu edo askeko ekuazioa lortzeko, zuzenean kalkula daiteke puntuaren koordenatuak eta maldaren balioa erabiliz.
Itxura esplizitu edo askeko ekuazioa lortzeko, zuzenean kalkula daiteke puntuaren koordenatuak eta maldaren balioa erabiliz.
Zuzena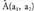 -tik eta
-tik eta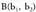 -tik igarotzen bada, bere malda honako hau izango du :
-tik igarotzen bada, bere malda honako hau izango du :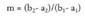 Malda kalkulatu ondoren, ekuazioa zuzenean idatz daiteke era
esplizituaren antzekoa den batean :
Malda kalkulatu ondoren, ekuazioa zuzenean idatz daiteke era
esplizituaren antzekoa den batean :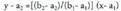 Adibidez, C(1,2) eta D(0,5) puntuetatik igarotzen den zuzenaren
ekuazio esplizitua, honako hau da :
Adibidez, C(1,2) eta D(0,5) puntuetatik igarotzen den zuzenaren
ekuazio esplizitua, honako hau da : ekuazio, edota sinplifikatuta :
ekuazio, edota sinplifikatuta :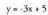 ekuazioa.
ekuazioa.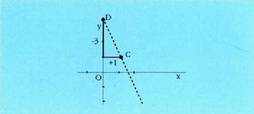 Puntuak koordenatu ardatzean baldin badaude, edota zuzen paraleloetan,
malda ezin daiteke kalkulatu. Adibidez, (2,3) eta (2,-1)
puntuetatik igarotzen den zuzenaren ekuazioa kalkulatuko balitz,
balio hau izango luke maldak :
Puntuak koordenatu ardatzean baldin badaude, edota zuzen paraleloetan,
malda ezin daiteke kalkulatu. Adibidez, (2,3) eta (2,-1)
puntuetatik igarotzen den zuzenaren ekuazioa kalkulatuko balitz,
balio hau izango luke maldak :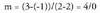
- Ariketak
7. Esazu ea P(-2,4) puntua ondoko zuzen hauetakoa den :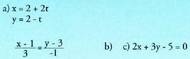 8. Emaitzazu zuzen hauetako hiruna puntu :
8. Emaitzazu zuzen hauetako hiruna puntu :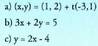
V. Bi zuzenen arteko ekuazioa.
Bi zuzen bat etor daitezke, izan daitezke elkarren ebakitzaileak
edota elkarrekiko paraleloak izan daitezke. Emandako bi zuzenen
arteko kokapen erlatiboak zeintzuk diren aztertzeko erarik egokiena,
beti ere, beren ekuazioak emanda dauden moduaren arabera
aukeratu beharko da.a) Bi ekuazioak bektore eran, parametro eran edo era jarraian
emanda baldin badaude, oso erraz jakiten da norabide bektoreak
zeintzuk diren eta zein puntutatik igarotzen diren :Bedi , zuzena,
, zuzena,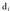 norabide bektorea duena eta
norabide bektorea duena eta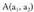 puntutik igarotzen dena eta halaber r2 zuzena, d2 norabide bektorea duena eta
puntutik igarotzen dena eta halaber r2 zuzena, d2 norabide bektorea duena eta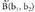 puntutik igarotzen dena. Hauetakoren bat gerta daiteke :
puntutik igarotzen dena. Hauetakoren bat gerta daiteke :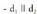 , bada, zuzenak paraleloak edo bat datozenak dira ;puntu ezagunetako bat, edozein, hartzen da, adibidez,
, bada, zuzenak paraleloak edo bat datozenak dira ;puntu ezagunetako bat, edozein, hartzen da, adibidez,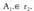 bada, orduan zuzenak bat datoz.
bada, orduan zuzenak bat datoz.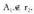 A, e r,. ez bada, orduan zuzenak paraleloak izango dira.
A, e r,. ez bada, orduan zuzenak paraleloak izango dira.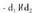 - d, 1Cd, bada, orduan zuzenak elkar ebakitzaileak dira.Adibidez, honako zuzenak emanda :
- d, 1Cd, bada, orduan zuzenak elkar ebakitzaileak dira.Adibidez, honako zuzenak emanda :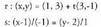 Norabide bektoreak, t(3,-1) biderkatzen duena eta ekuazio Jarraiko
(- 1, 1) izendatzailea dira. Bektore horiek ez dira proportzionalak,
beraz, bi zuzenak elkar ebakitzaileak dira.
Norabide bektoreak, t(3,-1) biderkatzen duena eta ekuazio Jarraiko
(- 1, 1) izendatzailea dira. Bektore horiek ez dira proportzionalak,
beraz, bi zuzenak elkar ebakitzaileak dira. Honako zuzen hauek izanda :
Honako zuzen hauek izanda : (1,1) eta (2,2) norabide bektoreak proportzionalak dira hurrenez
hurren, beraz, norabide berbera dute. r zuzenekoa den puntu bat, t = 0
balioarentzat (1,2) da. s zuzenaren ekuazioan ordezkatuta :
(1,1) eta (2,2) norabide bektoreak proportzionalak dira hurrenez
hurren, beraz, norabide berbera dute. r zuzenekoa den puntu bat, t = 0
balioarentzat (1,2) da. s zuzenaren ekuazioan ordezkatuta : , beraz, bi zuzenak paraleloak dira.
, beraz, bi zuzenak paraleloak dira.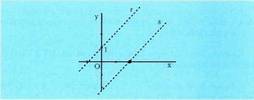 b) Ekuazioak era esplizitu edo inplizituan emanda baldin badaude,
bi ekuazio eta bi ezezagun dituen sistema moduan ezar daiteke.- Sistema bateragarria eta zehatza baldin bada, emaitza bakarra
du, ebaki puntua hain zuzen. Bi zuzenak elkar ebakitzaileak dira.- Ekuazioak bateragarriak eta zehazgabeak baldin badira,
emaitza kopuru infinitua du sistemak, eta bi zuzenak bat datoz.- Sistema bateragarria ez bada, emaitzarik ez dago eta bi zuzenak
paraleloak dira.Eztabaida oso erraza eta argia da bi zuzenak ekuazio esplizitu edo
askeen bitartez eman badira.
b) Ekuazioak era esplizitu edo inplizituan emanda baldin badaude,
bi ekuazio eta bi ezezagun dituen sistema moduan ezar daiteke.- Sistema bateragarria eta zehatza baldin bada, emaitza bakarra
du, ebaki puntua hain zuzen. Bi zuzenak elkar ebakitzaileak dira.- Ekuazioak bateragarriak eta zehazgabeak baldin badira,
emaitza kopuru infinitua du sistemak, eta bi zuzenak bat datoz.- Sistema bateragarria ez bada, emaitzarik ez dago eta bi zuzenak
paraleloak dira.Eztabaida oso erraza eta argia da bi zuzenak ekuazio esplizitu edo
askeen bitartez eman badira. baldin bada eta
baldin bada eta zuzenak bat datoz.
zuzenak bat datoz. baldin bada eta
baldin bada eta zuzenak paraleloak dira.
zuzenak paraleloak dira.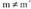 baldin bada bi zuzenek elkar ebakitzen dute.
baldin bada bi zuzenek elkar ebakitzen dute.
Adibidez,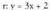 eta
eta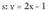 emanda,
emanda,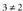 da, beraz, elkar ebakitzen dute.
da, beraz, elkar ebakitzen dute. eta
eta emanda,
emanda, da eta
da eta , beraz, paraleloak dira.
, beraz, paraleloak dira.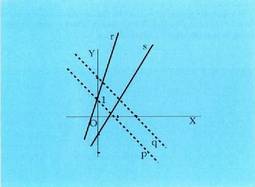 Ekuazioak era inplizituan emanda. Bitez ondorengo ekuazioak :
Ekuazioak era inplizituan emanda. Bitez ondorengo ekuazioak : bada, norabide bektoreak desberdinak dira eta bi zuzenek elkar ebakitzen dute.
bada, norabide bektoreak desberdinak dira eta bi zuzenek elkar ebakitzen dute. bada, norabide bektoreak proportzionalak dira.
bada, norabide bektoreak proportzionalak dira.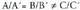 bada, bi ekuazioek ez dute emaitza komunik eta zuzenak paraleloak dira.
bada, bi ekuazioek ez dute emaitza komunik eta zuzenak paraleloak dira.
Adibidez, bitez: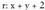 eta
eta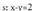 , orduan,
, orduan,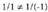 da eta elkar ebakitzen dute.
da eta elkar ebakitzen dute.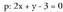 eta
eta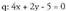 izanda
izanda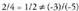 da, beraz, paraleloak dira.
da, beraz, paraleloak dira.
Aurkitu ebaki puntua.
Geometria analitikoan, elkar ebakitzen duten bi zuzen emanda,
ebaki puntua aurkitzea, ekuazio sistema bat ebaztea da.Ekuazioa era esplizituan, inplizituan edo jarraian emanak baldin
badaude, bi ekuazio eta bi ezezagun dituen sistema da. Adibidez,
kalkulatu ondorengo bi zuzen hauen ebaki puntua :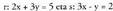 zuzenena alegia.Hiru metodoetako edozeinen bitartez egin daiteke kalkulua.
zuzenena alegia.Hiru metodoetako edozeinen bitartez egin daiteke kalkulua.
Laburketa metodoz honela egin daiteke :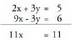 Emaitzak : x = 1 eta y = 1.
Emaitzak : x = 1 eta y = 1.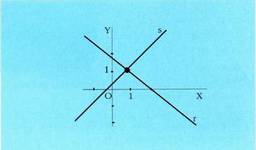 Ekuazioak era esplizituan emanda baldin badaude, adibidez, y = 3x
+ 2 eta y = 2x - 1, berdinketa bidezkoa da ebazteko modurik errazena :
Ekuazioak era esplizituan emanda baldin badaude, adibidez, y = 3x
+ 2 eta y = 2x - 1, berdinketa bidezkoa da ebazteko modurik errazena :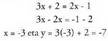 Ebazpena konplexuagoa da, baldin eta parametro edo bektoremoduan emanak baldin badaude. Bitez adibidez: r : (x,y) = (2, 1) +t(1,-1) eta
Ebazpena konplexuagoa da, baldin eta parametro edo bektoremoduan emanak baldin badaude. Bitez adibidez: r : (x,y) = (2, 1) +t(1,-1) eta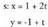 Lau ekuazioko sistema da lau ezezagunekin ; izan ere, bi parametroak,
bi ezezagun desberdin dira. Parametroak kendu eta x eta y-ren
arteko ekuazioak ebaztea da metodo bat.
Lau ekuazioko sistema da lau ezezagunekin ; izan ere, bi parametroak,
bi ezezagun desberdin dira. Parametroak kendu eta x eta y-ren
arteko ekuazioak ebaztea da metodo bat. Eragiketak eginez eta sinplifikatuz, ondorengo sistema lortzen da :
Eragiketak eginez eta sinplifikatuz, ondorengo sistema lortzen da :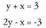 Emaitza
Emaitza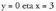 Parametroekin jarraitu nahi baldin bada, ez da ahaztu behar, bi zuzenentzat puntu komuna dena, orokorki, t parametroak bakoitzean balio desberdinak izanda lortuko dela. Beraz, hobe da hasierahasieratik batari t eta besteari
Parametroekin jarraitu nahi baldin bada, ez da ahaztu behar, bi zuzenentzat puntu komuna dena, orokorki, t parametroak bakoitzean balio desberdinak izanda lortuko dela. Beraz, hobe da hasierahasieratik batari t eta besteari deitzea.
deitzea.
Bitez adibidez :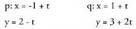 x eta y berdinak izan behar dute ebaki puntuan bi zuzenentzat, baina parametroak ez du zertan bi ekuazio bikoteetan berdina izanik.. zuzenaren parametroari
x eta y berdinak izan behar dute ebaki puntuan bi zuzenentzat, baina parametroak ez du zertan bi ekuazio bikoteetan berdina izanik.. zuzenaren parametroari deituta eta x eta y ordezkatuta, honela gelditzen da :
deituta eta x eta y ordezkatuta, honela gelditzen da :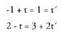 Sistema ebatzita, t=1 eta
Sistema ebatzita, t=1 eta ateratzen da. Hots, bi zuzenen ebaki puntua, x = 0 eta y = 1 da.
ateratzen da. Hots, bi zuzenen ebaki puntua, x = 0 eta y = 1 da.
Puntu batetik igarotzen den zuzen batekiko paraleloa.
Puntu jakin batetik igarotzen den zuzen batekiko paraleloa den
zuzenaren ekuazioa kalkulatzeko, zuzenaren norabidea kalkulatu
behar da ; ekuazio hori emandako zuzenaren berbera du, izan ere,
zuzen paralelo guztien sortak, norabide berbera baitu. Lerro paraleloaren
ekuazioa zein motatakoa den, aurkitu behar den zuzenaren
ekuazioa kalkulatzeko eman beharreko urratsak ere desberdinak
izango dira.Zuzena bektore, parametro edo ekuazio jarrai moduan emana
baldin badago, nahikoa da zuzena igarotzen den puntua aldatzea,
eta ekuazioaren gainerakoa berdin utzi. Adibidez :a) (x,y) = (3, -4) + t(2,-5) zuzenarekiko paraleloa den eta (5,1)
puntutik igarotzen den zuzenaren ekuazioa.Nahikoa da (3,-4) puntuaren koordenatuak (5,1)
gatik aldatzea, hau da, emaitza zera da :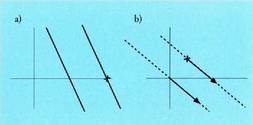 Zuzenaren ekuazioa era inplizituan emanda baldin badago, ezezagunen koefizienteek norabide bektorearen koordenatuak ematen dituzte. Beraz, Ax + By + C = 0 erako ekuazioa duen zuzen baten paraleloa den eta P(a,b) puntutik igarotzen den zuzenaren ekuazioa lortu nahi baldin bada, lerro paralelo horrek
Zuzenaren ekuazioa era inplizituan emanda baldin badago, ezezagunen koefizienteek norabide bektorearen koordenatuak ematen dituzte. Beraz, Ax + By + C = 0 erako ekuazioa duen zuzen baten paraleloa den eta P(a,b) puntutik igarotzen den zuzenaren ekuazioa lortu nahi baldin bada, lerro paralelo horrek itxura izango du.
itxura izango du.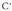 ren balioa, zuzena P puntutik igaro beharraren baldintza erabiliz kalkulatzen da. Honako hau bete behar du :
ren balioa, zuzena P puntutik igaro beharraren baldintza erabiliz kalkulatzen da. Honako hau bete behar du :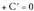 eta hortik
eta hortik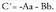 Adibidez,
Adibidez,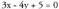 zuzenaren paraleloa izanik P(1,1) puntutik igaro behar duen zuzena,
zuzenaren paraleloa izanik P(1,1) puntutik igaro behar duen zuzena, da eta P-ren koordenatuak sartuta,
da eta P-ren koordenatuak sartuta,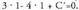 . Hortik,
. Hortik, ateratzen da.
ateratzen da.
Beraz, emaitza honako hau da: Zuzena era esplizituan emanda baldin badator, lerro paraleloak
ere malda berbera izan behar du, eta puntu jakin batetik igarotzeko
baldintzak gai askearen balioa kalkulatzeko aukera ematen du.Zuzena
Zuzena era esplizituan emanda baldin badator, lerro paraleloak
ere malda berbera izan behar du, eta puntu jakin batetik igarotzeko
baldintzak gai askearen balioa kalkulatzeko aukera ematen du.Zuzena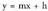 izanik, P(a,b) puntutik igarotzen den lerro paraleloaren ekuazioa
izanik, P(a,b) puntutik igarotzen den lerro paraleloaren ekuazioa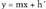 izango da. Hortik,
izango da. Hortik,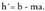 Adibidez, kalkulatu,
Adibidez, kalkulatu,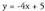 ekuaziodun zuzenaren paraleloa izanik jatorri puntutik igarotzen den zuzenaren ekuazioa. Jatorri puntutik igaro behar duelako, x=0 denean y=O izan behar du, beraz,
ekuaziodun zuzenaren paraleloa izanik jatorri puntutik igarotzen den zuzenaren ekuazioa. Jatorri puntutik igaro behar duelako, x=0 denean y=O izan behar du, beraz, eta jatorri puntutik igarotzen den zuzen paraleloa
eta jatorri puntutik igarotzen den zuzen paraleloa
- Ariketak
13. Esazu ea paraleloak, ebakitzaileak edo bat datozenak
diren ondoko zuzen bikoteak :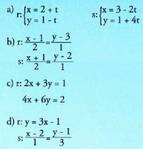 14. Kalkulatu ondoko zuzen hauen ebaki puntuak :
14. Kalkulatu ondoko zuzen hauen ebaki puntuak :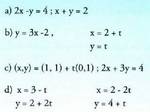
VI. Neurri ariketak : angeluak eta distantziak.
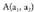 eta
eta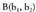 puntuen arteko destantzia,
puntuen arteko destantzia,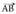 bektorearen modulu edo normaren balioa da, hau da :
bektorearen modulu edo normaren balioa da, hau da : Bektorearen normaren eitea, oinarri bektoreen araberakoa da.
Bektorearen normaren eitea, oinarri bektoreen araberakoa da.
Oinarria ortonormala baldin bada, distantziaren formula, Pitagorasen
teorematik itxaro daitekeenera mugatzen da. Kasu bereizi moduan, bi puntuak bat baldin badatoz, distantziak 0 ematen du eta ardatzen baten paraleloa den zuzenen batean baldin badaude, honela gelditzen da :
Kasu bereizi moduan, bi puntuak bat baldin badatoz, distantziak 0 ematen du eta ardatzen baten paraleloa den zuzenen batean baldin badaude, honela gelditzen da :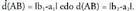 Adibidez : kalkulatuA(1,1) eta B(5,4) puntuen arteko distantzia, sistema orto nor malean emanda direla.
Adibidez : kalkulatuA(1,1) eta B(5,4) puntuen arteko distantzia, sistema orto nor malean emanda direla.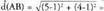 Kalkulatu A(2,2) eta B(6,2) puntuen arteko distantzia.
Kalkulatu A(2,2) eta B(6,2) puntuen arteko distantzia.
Bi zuzenen arteko angelua.
Bi zuzenen arteko angelua kalkulatzeko erarik erosoena, ekuazioak emandako moduaren arabera aurkitu behar da. Bi zuzenen norabide bektoreak erraz jakiteko modua baldin badago, biderkadura eskalarren bidez angeluaren kosinua kalkula daiteke.
Bedi zuzena
zuzena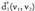 norabide bektorea duena eta bedi
norabide bektorea duena eta bedi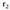 zuzena
zuzena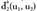 norabide bektorea duena.Hau betetzen da :
norabide bektorea duena.Hau betetzen da :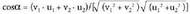 oinarri ortonormala duela suposatuta.Hortik erraz atera daiteke biek eratzen duten angeluaren kosinua.
oinarri ortonormala duela suposatuta.Hortik erraz atera daiteke biek eratzen duten angeluaren kosinua.
Bi zuzenek lau angelu eratzen dituzte gurutzatzean eta angelu horiek bizbitara hartuta berdinak dira. Kosinuarekin zuzenean lortzen den angeluaren balioa, hartu diren norabide bektoreen arabera, izan daiteke angelu zorrotzarena ala kamutsarena.
Adibidez,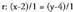 eta
eta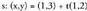 zuzenen arteko angelua kalkulatzeko, errazki ikusten da, norabide bektoreak
zuzenen arteko angelua kalkulatzeko, errazki ikusten da, norabide bektoreak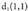 eta
eta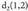 direla eta beren arteko angeluaren k osinua on dorengoa da :
direla eta beren arteko angeluaren k osinua on dorengoa da : eta hortik
eta hortik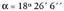 ateratzen da.
ateratzen da.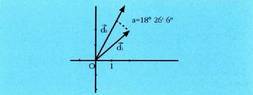 Bi bektoreek norabide berbera baldin badute,
Bi bektoreek norabide berbera baldin badute,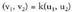 da eta
da eta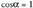 , beraz angeluak
, beraz angeluak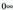 balio du.Bi bektore horiek elkartzutak baldin badira, cosa = 0 izan behar
du, hau da, elkartzutasun baldintza honako hau da :
balio du.Bi bektore horiek elkartzutak baldin badira, cosa = 0 izan behar
du, hau da, elkartzutasun baldintza honako hau da :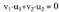 eta hauxe esan nahi du, alegia, bi zuzen elkartzutak baldin badira,
horien norabide bektoreek ondorengoa betetzen dutela :
eta hauxe esan nahi du, alegia, bi zuzen elkartzutak baldin badira,
horien norabide bektoreek ondorengoa betetzen dutela :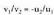 Adibidez,
Adibidez,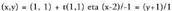 zuzenak, elkartzutak dira, izan ere,
zuzenak, elkartzutak dira, izan ere, betetzen baitute.
betetzen baitute. Orokorki, emandako bektore bati buruz zuta den beste bat nahi
baldin bada, emandako bektorea (a,b) izanda, bektore perpendikularra,
(-b,a) da.Ekuazioa era inplizituan emanda baldin badago : Ax + By + C = 0,
norabide bektore bat (-B,A) da, beraz, zuzenari buruz zuta den bektorea
(A,B) da. Era inplizituan emandako bi zuzenen artean eratutako
angelua kalkulatzeko, lehendabizi beren norabide bektoreak
kalkulatzen dira.Bitez
Orokorki, emandako bektore bati buruz zuta den beste bat nahi
baldin bada, emandako bektorea (a,b) izanda, bektore perpendikularra,
(-b,a) da.Ekuazioa era inplizituan emanda baldin badago : Ax + By + C = 0,
norabide bektore bat (-B,A) da, beraz, zuzenari buruz zuta den bektorea
(A,B) da. Era inplizituan emandako bi zuzenen artean eratutako
angelua kalkulatzeko, lehendabizi beren norabide bektoreak
kalkulatzen dira.Bitez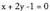 eta
eta ekuazioak. Beren arteko angelua kalkulatzeko beren norabide bektoreak kalkulaten dira :
ekuazioak. Beren arteko angelua kalkulatzeko beren norabide bektoreak kalkulaten dira :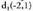 eta
eta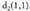 . Eratzen duten angeluaren kosinuaren balioa ondorengoa da:
. Eratzen duten angeluaren kosinuaren balioa ondorengoa da: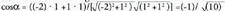 Beraz,
Beraz,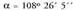 da.
da. norabide bektorea hartu izan bagenu, bi zuzenek elkarren artean eratzen duten beste angeluaren balioa aterako zatekeen, hots, betegarriarena :
norabide bektorea hartu izan bagenu, bi zuzenek elkarren artean eratzen duten beste angeluaren balioa aterako zatekeen, hots, betegarriarena :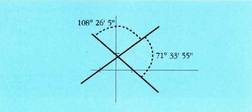 Ekuazioa era esplizituan emanda baldin badator : y = mx + h, zera
idatz daiteke, mx - y + h = 0 eta norabide bektore bat (l,m) da.
Ekuazioa era esplizituan emanda baldin badator : y = mx + h, zera
idatz daiteke, mx - y + h = 0 eta norabide bektore bat (l,m) da.
Zuzenean ere egin daiteke ordea, m = tga erabiliz, bertan a zuzenaten zeihartasuna edo inklinazioa dela, edota bestela esanda, abzisa ardatzaren norantza positiboarekin eratzen duen angelua alegia. Era esplizituan emandako bi zuzenen arteko angelua kalkulatzeko, zera hartuko dugu kontuan, alegia, eratzen duten a angelua, bi zuzenek dituzten eta
eta zeihartasun angeluen arteko diferentzia dela :
zeihartasun angeluen arteko diferentzia dela :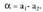 Bi angeluen arteko diferentzia den angeluaren tangenteak hau
betetzen du :
Bi angeluen arteko diferentzia den angeluaren tangenteak hau
betetzen du :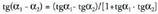 hau da :
hau da :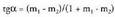 Adibidez,
Adibidez,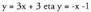 zuzenek eratzen duten angelua kalkulatzeko, honela egin daiteke : maldak
zuzenek eratzen duten angelua kalkulatzeko, honela egin daiteke : maldak eta
eta dira, beraz:
dira, beraz: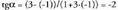 Hortik ateratzen da
Hortik ateratzen da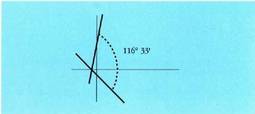 Bi zuzen paraleloak edota bat datozenak dira baldin eta beren arteko angelua zero baldin bada, eta beraz, angelu horren tangentea ere bai. Orduan zenbakitzaileak zero izan beharko du, hau da,
Bi zuzen paraleloak edota bat datozenak dira baldin eta beren arteko angelua zero baldin bada, eta beraz, angelu horren tangentea ere bai. Orduan zenbakitzaileak zero izan beharko du, hau da, , lehen ateratako baldintza hain zuzen ere.Bi zuzen elkartzutak baldin badira, beren arteko angelua 90°-koa da eta 90°-ko angeluaren tangentea infinitu da. Beraz, izendatzaileakzero izan beharko du:
, lehen ateratako baldintza hain zuzen ere.Bi zuzen elkartzutak baldin badira, beren arteko angelua 90°-koa da eta 90°-ko angeluaren tangentea infinitu da. Beraz, izendatzaileakzero izan beharko du: edota
edota Emandako zuzen jakin bati buruz zuta den eta puntu jakin batetik igarotzen den zuzenaren ekuazioa jakin nahi baldin badugu, ezaugarri hauek erabiltzen dira.Adibidea: 1. Kalkulatu (x-1)/2 = y/3 zuzenari buruz zuta den eta (3,-1) puntutik igarotzen den zuzenaren ekuazioa.
Emandako zuzen jakin bati buruz zuta den eta puntu jakin batetik igarotzen den zuzenaren ekuazioa jakin nahi baldin badugu, ezaugarri hauek erabiltzen dira.Adibidea: 1. Kalkulatu (x-1)/2 = y/3 zuzenari buruz zuta den eta (3,-1) puntutik igarotzen den zuzenaren ekuazioa.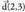 norabide bektoreari buruz zuta den bektore bat,
norabide bektoreari buruz zuta den bektore bat,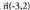 bektorea da, beraz, zuzen elkartzutaren ekuazioa,
bektorea da, beraz, zuzen elkartzutaren ekuazioa,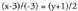 izango da.2. Kalkulatu y = 3x + 1 zuzenari buruz zuta den eta (1,0) puntutik
igarotzen den zuzenaren ekuazioa. Malda m = 3 da, beraz, elkartzutaren
malda, m = (-1)/3 izango da eta orduan y = (-1/3)x + h
izango da bere ekuazioa. Gainera, x = 1 baldin bada, y = 0 izan behar
du eta ekuazioak honako hau bete behar du : 0 = (-1/3) + h. Hortik,
h = 1/3. Beraz, elkartzuta den eta puntu horretatik igarotzen den
zuzenaren ekuazioa, hau izango da :
izango da.2. Kalkulatu y = 3x + 1 zuzenari buruz zuta den eta (1,0) puntutik
igarotzen den zuzenaren ekuazioa. Malda m = 3 da, beraz, elkartzutaren
malda, m = (-1)/3 izango da eta orduan y = (-1/3)x + h
izango da bere ekuazioa. Gainera, x = 1 baldin bada, y = 0 izan behar
du eta ekuazioak honako hau bete behar du : 0 = (-1/3) + h. Hortik,
h = 1/3. Beraz, elkartzuta den eta puntu horretatik igarotzen den
zuzenaren ekuazioa, hau izango da :
- Ariketak
19. Kalkula ezazu ondoko zuzen hauek elkarren artean
eratzen dituzten angeluak :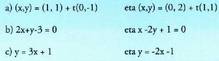 20. Kalkula ezazu r zuzenari buruz zuta den eta P puntutik
igarotzen den zuzenaren ekuazioa
20. Kalkula ezazu r zuzenari buruz zuta den eta P puntutik
igarotzen den zuzenaren ekuazioa
Puntu batek zuzenean duen proiekzioa :
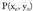 puntua izanik, zuzen batean puntu horrek duen proiekzioa zein den jakin nahi da. Bedi zuzena ondoko ekuazioa hauek dituena:
puntua izanik, zuzen batean puntu horrek duen proiekzioa zein den jakin nahi da. Bedi zuzena ondoko ekuazioa hauek dituena: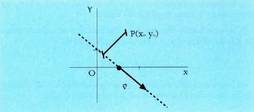 Horretarako, zuzen horrek
Horretarako, zuzen horrek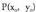 puntutik marraztutako elkartzutarekin duen ebaki puntua aurkitzen da.
puntutik marraztutako elkartzutarekin duen ebaki puntua aurkitzen da.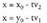 Zuzenaren ekuazioa era inplizituan emanda baldin
elkartzuta honako hau izango da :
Zuzenaren ekuazioa era inplizituan emanda baldin
elkartzuta honako hau izango da :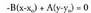 Era esplizituan edo askean badago berriz :
Era esplizituan edo askean badago berriz :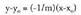 Adibidez, P(6,3) puntuak 2x-y+1=0 zuzenean duen proiekzioa
jakin nahi baldin bada, P puntutik igarotzen den elkartzuta kalkulatzen
da lehendabizi ; kasu honetan honako eite hau izango du :
Adibidez, P(6,3) puntuak 2x-y+1=0 zuzenean duen proiekzioa
jakin nahi baldin bada, P puntutik igarotzen den elkartzuta kalkulatzen
da lehendabizi ; kasu honetan honako eite hau izango du :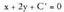 P-tik pasa behar duenez,
P-tik pasa behar duenez, bete behar du, beraz,
bete behar du, beraz, izango da. Beraz, elkartzutaren ekuazioa
izango da. Beraz, elkartzutaren ekuazioa da.
da. zuzenaren eta
zuzenaren eta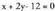 elkartzutaren arteko ebaki puntua ekuazioen ebazpenetik etorriko da. Adibidez, bigarren ekuazioan
elkartzutaren arteko ebaki puntua ekuazioen ebazpenetik etorriko da. Adibidez, bigarren ekuazioan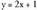 ordezkatuta :
ordezkatuta :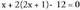 gelditzen da eta hortik:
gelditzen da eta hortik: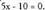 . Beraz,
. Beraz, eta
eta
Puntu batek zuzen batekiko duen simetria puntua.
P puntuak r zuzenarekiko duen simetria puntua, zuzenetik distantzia berberera baina zuzenak beste aldeko planoerdian eta puntu horretatik zuzenarekiko marraztutako elkartzutean dagoena du.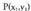 , puntuaren r zuzenarekiko simetria puntua den
, puntuaren r zuzenarekiko simetria puntua den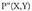 puntua aurkitzeko, aurreko prozeduraren bitartez proiekzioa aurkitzen da eta ondoren simetria puntuaren koordenatuak ateratzen dira,
puntua aurkitzeko, aurreko prozeduraren bitartez proiekzioa aurkitzen da eta ondoren simetria puntuaren koordenatuak ateratzen dira, proiekzioa, emandako puntuaren eta bere simetrikoaren arteko erdibideko puntua dela kontuan hartuta beti ere. Horrela bada :
proiekzioa, emandako puntuaren eta bere simetrikoaren arteko erdibideko puntua dela kontuan hartuta beti ere. Horrela bada :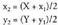 non (X,Y) aurkitu nahi dugun puntua den.Adibidez, kalkulatu P(3,1) puntuaren r: x+y=O zuzenarekikosimetria puntua.P-tik igaro eta r lerroari buruz zuta den zuzena, (x-3)-(y-1)=O da.Bi zuzenen ebaki puntua, M(1,-1) da :(3+X)/2 = 1 da eta hortik X = -1(1+Y)/2 = -1 da eta hortik Y = -3Beraz, simetria puntua
non (X,Y) aurkitu nahi dugun puntua den.Adibidez, kalkulatu P(3,1) puntuaren r: x+y=O zuzenarekikosimetria puntua.P-tik igaro eta r lerroari buruz zuta den zuzena, (x-3)-(y-1)=O da.Bi zuzenen ebaki puntua, M(1,-1) da :(3+X)/2 = 1 da eta hortik X = -1(1+Y)/2 = -1 da eta hortik Y = -3Beraz, simetria puntua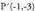 da.
da.
- Ariketak
21. kalkula ezazu P(1,1) puntuaren x = 1 + t eta y = 2 zuzenarekiko simetria puntua.
VII. Puntu batetik zuzen batera bitarteko distantzia.
Orokorki, puntu batetik zuzen batera bitarteko distantzia aurkitzeko,
lehendabizi puntu horrek zuzen horretan duen proiekziopuntua kalkula daiteke eta ondoren puntutik proiekzio punturainoko
distantzia kalkulatu. Zuzen bat eta puntu bat emanda, emandako
zuzenari buruz perpendikular puntu horretatik igarotzen den
zuzenaren ekuazioa kalkulatu behar da eta ondoren bien ebaki puntua
aurkitu. Bi puntuen emandakoaren eta ebaki puntuaren) arteko
distantzia da aurkitu nahi zen distantzia.Kalkulu hau sinplifika daiteke ekuazioa era inplizituan emanda baldin badago. Bedi Ax + By + C = 0 zuzenaren ekuazioa eta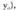 , zuzeneraino distantzia kalkulatu nahi den puntua. P-tik r-rainoko distantzia, jatorri puntutik r zuzenarekiko paraleloa den lerrorainoko distantzia ken jatorritik r zuzenerainokoa izango da.
, zuzeneraino distantzia kalkulatu nahi den puntua. P-tik r-rainoko distantzia, jatorri puntutik r zuzenarekiko paraleloa den lerrorainoko distantzia ken jatorritik r zuzenerainokoa izango da.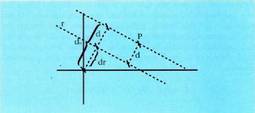 P-tik igarotzen den r zuzenaren paraleloaren ekuazioa, honako hau da :
P-tik igarotzen den r zuzenaren paraleloaren ekuazioa, honako hau da :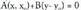 Jatorri puntutik lerro paralelo horretarako distantzia, jatorri puntua zuzeneko puntu batekin lotzen duen edozein bektorek zuzen elkartzutean duen proiekzioaren berdina izango da. Har dezagun
Jatorri puntutik lerro paralelo horretarako distantzia, jatorri puntua zuzeneko puntu batekin lotzen duen edozein bektorek zuzen elkartzutean duen proiekzioaren berdina izango da. Har dezagun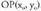 . Zuzen horri buruz zuta den bektore unitarioa (edo unitate bektorea), honako hau da :
. Zuzen horri buruz zuta den bektore unitarioa (edo unitate bektorea), honako hau da :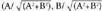 , izan ere, zuzenaren norabide bektorea (-B, A) baita eta horren bektore elkartzuta (A, B) izango da. Baldin eta bektore horren moduluaz biderkatua gerta ez dadin, bektorea unitarioa izatea nahi badugu,
, izan ere, zuzenaren norabide bektorea (-B, A) baita eta horren bektore elkartzuta (A, B) izango da. Baldin eta bektore horren moduluaz biderkatua gerta ez dadin, bektorea unitarioa izatea nahi badugu,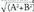 balioaz zatitu beharko genuke. Beraz, distantzia, zeinu eta guzti honako hau izango da :
balioaz zatitu beharko genuke. Beraz, distantzia, zeinu eta guzti honako hau izango da :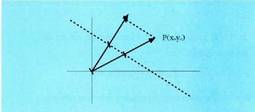 Zuzeneko edozein puntu P(x,y) izango da. Jatorri punturako distantzia,
zeinu berarekin hartuta, hau izango da :
Zuzeneko edozein puntu P(x,y) izango da. Jatorri punturako distantzia,
zeinu berarekin hartuta, hau izango da :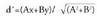 Diferentzia :
Diferentzia :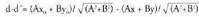 (x,y) zuzenean egoteagatik, hau bete behar du :
(x,y) zuzenean egoteagatik, hau bete behar du :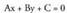 beraz, Ax + By = -Ceta aurkitu nahi dugun distantzia honela gelditzen da :
beraz, Ax + By = -Ceta aurkitu nahi dugun distantzia honela gelditzen da :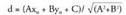 Puntu batetik zuzenerako distantzia.Ikus ezazu, alegia, zuzenari buruz zuta edo normala den bektorearen norantzaren arabera,
Puntu batetik zuzenerako distantzia.Ikus ezazu, alegia, zuzenari buruz zuta edo normala den bektorearen norantzaren arabera,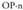 biderkadura eskalarrak zeinu bat ala aurkakoa har lezakeela, izan ere, angelua, a izatetik
biderkadura eskalarrak zeinu bat ala aurkakoa har lezakeela, izan ere, angelua, a izatetik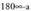 izatera igarotzen baita eta orduan kosinua zeinuz aldatzen da. Horren ondorioz, formula horrek, distantzia zeinu eta guzti ematen du, hau da, zuzenak planoa zatitzen duen bi planoerdietako batean, zeinua negatiboa ateratzen da eta bestean positiboa, beraz, formulari balio absolutua bakarrik jartzen zaio, distantziak beti positiboak direlako.
izatera igarotzen baita eta orduan kosinua zeinuz aldatzen da. Horren ondorioz, formula horrek, distantzia zeinu eta guzti ematen du, hau da, zuzenak planoa zatitzen duen bi planoerdietako batean, zeinua negatiboa ateratzen da eta bestean positiboa, beraz, formulari balio absolutua bakarrik jartzen zaio, distantziak beti positiboak direlako.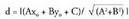 Adibidea:1. Kalkulatu P(2,1) puntutik x-y+4=0 zuzenerako distantzia.Formula erabiliz :
Adibidea:1. Kalkulatu P(2,1) puntutik x-y+4=0 zuzenerako distantzia.Formula erabiliz :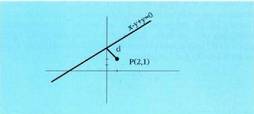 2. P(3,-2) puntutik x + y -1 = 0 zuzenerako distantzia.Formula erabiliz :
2. P(3,-2) puntutik x + y -1 = 0 zuzenerako distantzia.Formula erabiliz :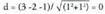
Bi zuzen paraleloen arteko distantzia.
Bi zuzen paraleloen arteko distantzia kalkulatzeko, bietako batean,
edozeinetan, puntu bat hautatu eta hortik beste zuzenera dagoen
distantzia kalkulatzen da.Adibidez, kalkulatu zuzenetik
zuzenetik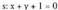 zuzenerako distantzia.r zuzeneko puntu bat Q (1,2) da adibidez.
zuzenerako distantzia.r zuzeneko puntu bat Q (1,2) da adibidez.
- Ariketak
22. Kalkulatu P(3,5) puntutik 5x-12Y+20=0 zuzenerako distantzia.23. Kalkulatu r : (x-1)/2 = (y-2)/3 zuzenetik s : (x,y) = (1,2) + t(2,3) zuzenerako distantzia.
VIII. Zuzenak diren leku geometrikoak.
Geometria analitikoak leku geometrikoen problema batzuek
erraz ebazteko aukera ematen du, edota bestela esanda, baldintza
jakin bat betetzen duten planoko puntuen multzoa aurkitzea alegia.
Kasu horiek ebazteko, zuzen eta puntuen arteko gorabeheretan
nahiz paralelotasun, elkartzutasun eta distantzia kontuetan aurkitutakoak
erabiliko dira.
Zuzenki baten erdibitzailea.
Erdibitzailea, zuzenki baten bi muturretatik distantziakide diren
puntuen leku geometrikoa da.Beraz,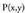 erdibitzaileko puntu bat bada eta zuzenkiaren muturrak
erdibitzaileko puntu bat bada eta zuzenkiaren muturrak eta
eta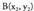 badira, erdibitzaileko puntuek honako hau bete behar dute :
badira, erdibitzaileko puntuek honako hau bete behar dute :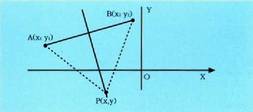 izan ere, muturretatik distantziakide baitira. Karratua eginez :
izan ere, muturretatik distantziakide baitira. Karratua eginez :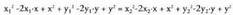 x eta y karratuak dituzten gaiak sinplifikatuta eta gai baliokideak
bilduta, hau gelditzen da :
x eta y karratuak dituzten gaiak sinplifikatuta eta gai baliokideak
bilduta, hau gelditzen da :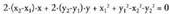 Malda
Malda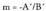 duen zuzena da, non
duen zuzena da, non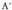 eta
eta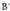 ekuazio inplizituko x eta y gaien koefizienteak diren. Bestela esanda :
ekuazio inplizituko x eta y gaien koefizienteak diren. Bestela esanda :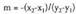 Malda hori bi puntuak elkartzen dituen zuzenaren elkartzutari
dagokio. Bi puntuak elkartzen dituen lerroari berriz, beste malda
hau dagokio :
Malda hori bi puntuak elkartzen dituen zuzenaren elkartzutari
dagokio. Bi puntuak elkartzen dituen lerroari berriz, beste malda
hau dagokio :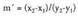 Beste era batera ere egiazta daiteke, alegia, erdibitzailearen ekuazioan (x,y) koordenatuak
Beste era batera ere egiazta daiteke, alegia, erdibitzailearen ekuazioan (x,y) koordenatuak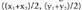 balioaz ordezkatuz, izan ere, erdibitzailea zuzenkiaren erdi-erdiko puntutik igarotzen baita itxaro zitekeenaren arabera.Adibidea :Kalkula ezazu A(1,2), B(4,3) puntuak muturtzat dituen zuzenkiaren
erdibitzailearen ekuazioa.Erdibitzailea izateagatik, hau bete behar du :
balioaz ordezkatuz, izan ere, erdibitzailea zuzenkiaren erdi-erdiko puntutik igarotzen baita itxaro zitekeenaren arabera.Adibidea :Kalkula ezazu A(1,2), B(4,3) puntuak muturtzat dituen zuzenkiaren
erdibitzailearen ekuazioa.Erdibitzailea izateagatik, hau bete behar du :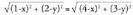 Karratua kalkulatu eta sinplifikatuta :
Karratua kalkulatu eta sinplifikatuta :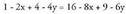 Gai guztiak alde batera pasata :
Gai guztiak alde batera pasata :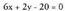 Sinplifikatuta :
Sinplifikatuta :
Erdikaria.
Erdikaria angelu bat bi angelu berdinetan zatitzen duen zuzenerdia da. Angeluaren aldeetatik distantziakide diren puntuen leku geometrikoa ere bada ; ezaugarri horrek errazago eman dezake aurkitu nahi den zuzenaren ekuazioa. ekuaziodun bi zuzen emanda, puntu batetik zuzen baterako distantzia, lehen kalkulatu den formularen bitartez ateratzen da.
ekuaziodun bi zuzen emanda, puntu batetik zuzen baterako distantzia, lehen kalkulatu den formularen bitartez ateratzen da.
Idazpen hori bi zuzenekin berdinduta, erdikariko puntu orokor batentzat, ondorengoa lortzen dugu :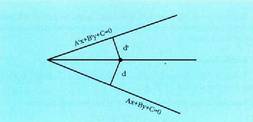 Sinplifikatzeko lehenengo urratsa balio absolutua kentzea da.
Sinplifikatzeko lehenengo urratsa balio absolutua kentzea da.
Distantziak zeinu positiboduntzat hartzen dira, baina balio absolutu
hori kentzean, bi zeinuak gertatzen dira baliodunak. Horrek bi
lerro erdikari ematen ditu. Horietako bat, interesatzen zaizkigun
zuzenerdiena edota beren luzapenena da ; bestea berriz, zuzenerdi
horietako batek eta beste zuzenerdiaren luzapenak eratzen duten
angelu betegarriarena. Ateratzen diren erdikarien bi ekuazioak
elkartzutak dira. Bietatik bat bakarrik interesatzen den kasuan
baliozkoa zein den jakiteko, malda azter daiteke. Erdikariaren
malda, bera erdikari duten bi zuzenerdiek dituzten malden tarteko
balioduna da.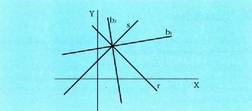 Adibidea : Kalkula ezazu 3x - 4y + 2 = 0 eta 12x + 5y - 3 = 0 zuzenen
erdibitzailea, bi zuzenetarako distantziak berdinak izanaraziz :
Adibidea : Kalkula ezazu 3x - 4y + 2 = 0 eta 12x + 5y - 3 = 0 zuzenen
erdibitzailea, bi zuzenetarako distantziak berdinak izanaraziz :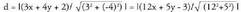 Balio absolutua kendu eta erroak kalkulatuta :
Balio absolutua kendu eta erroak kalkulatuta :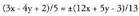 Bi emaitza ateratzen dira :
Bi emaitza ateratzen dira :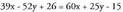 eta
eta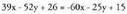 Hau da :
Hau da :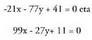 Bereizi beharrik izanez gero, lehenengoak malda txikia eta negatiboa
du eta bigarrenak handia eta positiboa.
Bereizi beharrik izanez gero, lehenengoak malda txikia eta negatiboa
du eta bigarrenak handia eta positiboa.
- Ariketak
24. Kalkula ezazu A(-1,2) eta B(3,-2) muturtzat dituen zuzenkiaren erdibitzaileak duen ekuazioa.25. Kalkula itzazu x+y-2=0 eta x-y-1=0 zuzenen erdibitzaileak .
IX. Triangelua.
Aurreko atalean ikusiak triangeluetan erdibitzaile, erdikari eta
alturei dagozkien ariketak ebazteko aukera ematen du.Adibidea : Bedi A(O,O), B(0,4) eta C(2,2) erpinak dituen triangelua
. Kalkulatu zirkunzentroa eta zirkunskribatutako zirkunferentziaren
erradioa, inzentroa eta triangeluan inskribatutako zirkunferentziaren
erradioa.a) Erdibitzaileen ekuazioak honako hauek dira :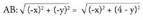 Sinplifikatuta : y = 2
Sinplifikatuta : y = 2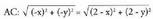 Sinplifikatuta : x+y-2=0
Sinplifikatuta : x+y-2=0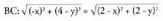 Sinplifikatuta : x - y + 2 = 0Zirkunzentroa horien ebaki puntua da ; puntu hori D(0,2) da.
Sinplifikatuta : x - y + 2 = 0Zirkunzentroa horien ebaki puntua da ; puntu hori D(0,2) da.
Zirkunferentzia zirkunskribatuaren erradioa, zirkunzentrotik erpinetako
edozeinetara dagoen distantzia da, hots,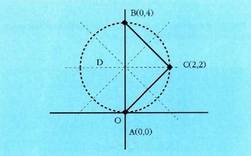 Inzentroa kalkulatzeko, erdikarien ekuazioak kalkulatzen dira ; bi
aldeen ekuazioak jakin behar dira horretarako :
Inzentroa kalkulatzeko, erdikarien ekuazioak kalkulatzen dira ; bi
aldeen ekuazioak jakin behar dira horretarako :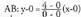 malda infinitua duen x=0 ekuaziodun zuzena da.
malda infinitua duen x=0 ekuaziodun zuzena da.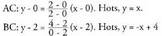 Erdibitzaileak honako hauek dira: AB eta AC - rena:
Erdibitzaileak honako hauek dira: AB eta AC - rena: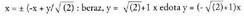 Maldari begiratuta, barneko erdikaria lehenengoa da.AC eta BC-rena :
Maldari begiratuta, barneko erdikaria lehenengoa da.AC eta BC-rena :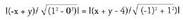 Sinplifikatuta, x = 2 eta y = 2 gelditzen dira. Bigarrena barneko
erdikaria da.AB eta BC-rena :
Sinplifikatuta, x = 2 eta y = 2 gelditzen dira. Bigarrena barneko
erdikaria da.AB eta BC-rena :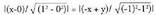 Sinplifikatuta,
Sinplifikatuta,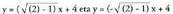 Malda negatibodun erdikaria, hots, bigarrena da barneko erdikaria.I inzentroa, erdikarien ebaki puntua da, hots,
Malda negatibodun erdikaria, hots, bigarrena da barneko erdikaria.I inzentroa, erdikarien ebaki puntua da, hots,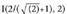 Zirkunferentzia inskribatuaren erradioa, inzentrotik aldeetako edozeinetara dagoen distantzia da. AB aldera duen distantzia da aurkitzen errazena, ekuazioa x=0 duen alderako distantzia alegia.
Zirkunferentzia inskribatuaren erradioa, inzentrotik aldeetako edozeinetara dagoen distantzia da. AB aldera duen distantzia da aurkitzen errazena, ekuazioa x=0 duen alderako distantzia alegia.
Distantzia hori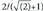 da. Beraz, inskribatutako zirkunferentziaren erradioak
da. Beraz, inskribatutako zirkunferentziaren erradioak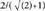 balio du.
balio du.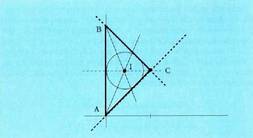
Erdibidekoa.
Edozein ABC triangelu emanik, erdibidekoen G ebaki puntuak hau betetzen du : Bestalde ordea, paralelogramoaren araua kontuan hartuta :
Bestalde ordea, paralelogramoaren araua kontuan hartuta :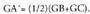 Beraz, triangeluaren barizentroa berdintza hau betetzen duen
puntua da :
Beraz, triangeluaren barizentroa berdintza hau betetzen duen
puntua da :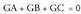 Beraz, hiru erpinetara bideratutako bektoreen batura zero da.
Beraz, hiru erpinetara bideratutako bektoreen batura zero da.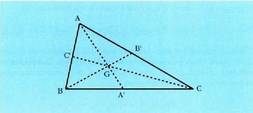 Barizentroa hiru erpinei garrantzi berbera ematen ez zaien kasurako
eta hiru puntu baino gehiagoz ari garenerako orokortzen da.Barizentroa, orokorki, honela definitzen da :
Barizentroa hiru erpinei garrantzi berbera ematen ez zaien kasurako
eta hiru puntu baino gehiagoz ari garenerako orokortzen da.Barizentroa, orokorki, honela definitzen da : erako n puntu emanik eta masa deritzen beste n zenbaki erreal m ; (!akoitza puntu horietako bakoitzean kokatua), denen artean
erako n puntu emanik eta masa deritzen beste n zenbaki erreal m ; (!akoitza puntu horietako bakoitzean kokatua), denen artean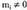 baldintza betetzen dutenak,
baldintza betetzen dutenak,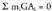
Emaitzak.
 Beste aukera asko ere badaude.
Beste aukera asko ere badaude.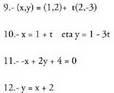 13.- a) Ebakitzaileak b) Bat datoz c) Bat datoz d) Paraleloak
13.- a) Ebakitzaileak b) Bat datoz c) Bat datoz d) Paraleloak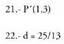 23.- d = 0, beraz bi zuzenak bat datoz.
23.- d = 0, beraz bi zuzenak bat datoz.