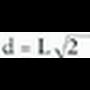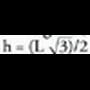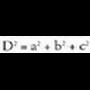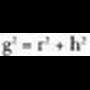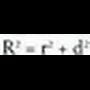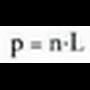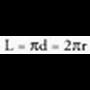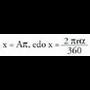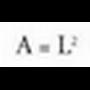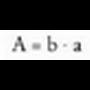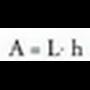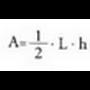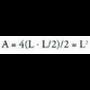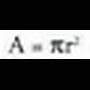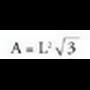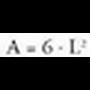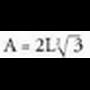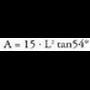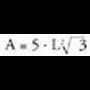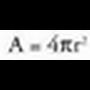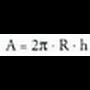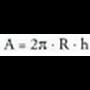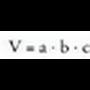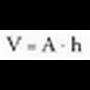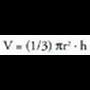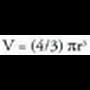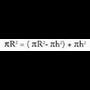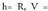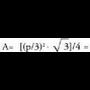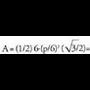Matematika»Geometria
Luzerak, areak eta bolumenak
I. Neurriaren definizioa
Zuzenkiak berdinak direla esan ohi da, eta orobat angeluak,
elkarren gainean jarri eta bat datozenean. Baliokidetasun erlazio
guztiak bezala, berdintasun hori simetrikoa, iragankorra eta erreflexiboa
da. Horrez gainera, badago definitzerik zuzenkien batura
bat, edo angeluena, zenbaki baturaren arauak betetzen dituena ;
alegia, elkarkorra da, trukakorra, badu elementu neutrorik, eta,
orientazioak onartzen badira, baita elkarren aurkako elementuak
ere. Elementu, zuzenki edo angelu berdinez, esaten da magnitude
bera dutela, tasun horretxek egiten baititu berdin, edo tasun
horietxei esker batu daitezke. Bestalde, kasu horietan magnitudea
osorik ordena daiteke, eta horregatik esaten da luzerak eta angeluak
magnitude eskalarrak direla. Badira beste geometria tasun batzuk
ere, hala adibidez zuzenen paralelotasuna : baliokidetasun erlazioa
da, baina batuketa ez du onartzen, eta, hortaz, ez da magnitudea.
Beste zenbait kasutan, bektoreen kasuan adibidez, magnitude bat
berdintasun baten bidez definitzen da (ekipolentziaz), eta operazio
batzuen bidez (bi bektoreren batuketaz) ; baina ordena oso bat ezin
da definitu, eta, hori dela-eta, esaten da magnitude hori ez dela
eskalarra.Bestalde, angeluetan edo zuzenkietan definituriko magnitudeek
zenbaki errealen tasun topologikoak ere badituzte, hala adibidez
jarraituak edo Arkimedesenak izatea.Horrela bada, magnitude jakin baten eta zenbaki errealen arteko
korrelazio baten definizioa eman daiteke. Korrespondentzia hori
egiteko, zein angelu edo zuzenkiri dagokion R-ko banakoa finkatu
beharra dago aurrena. Banakoa jakinda, eta kontuan hartuta korrespondentziak
isomorfismoa behar duela izan, alegia, O-a dagokiola
elementu baliogabeari, zenbaki batura magnitude baturari, etab.,
zuzenki edo angelu bakoitzak bere neurria emango duen zenbaki
erreal bat izango du : luzera zuzenkia bada edo zabaltasuna angelua
bada.Zuzenki bat neurtzea, banakoa emanik, zein den zuzenki
horren luzerari dagokion zenbakia jakitea da. Neurri hori aurkitzea
gauza erraza da neurtu nahi den zuzenkia eta banakoa aldera
daitezkeenean, hau da, zuzenkia banakoa aldi finituz biderkatua
denean, edo banakoa aldi finituz biderkaturik berdin zuzenkia
zenbaki osoz biderkatua denean. Hau da, x luzeraren eta u banakoaren
artean egiaztatzen bada x = un edo px = qu (n, p eta q zenbaki
osoak izanik), neurtzea erraza izango da, emaitza zenbaki oso
bat edo zatiki bat izango baita. Kasu honetan zuzenki hori neurgarria
dela esaten da, banako hori erabiliz. Era horretako berdintasunik
ezin ezarri baldin bada, zuzenkia neurtezina dela esaten
da. Laukiaren diagonala, adibidez, aldea bat baldin badu, zuzenki
neurtezina da. Kasu horretan, bi zatiki segida izango dira, neurriaz
goitikoak eta behetikoak, eta horiei dagokien ebakidura izango da
zuzenkiaren neurria.Era horretan, egokitasun bat sortzen da zuzenkien eta zenbakien
artean, edo zuzenkien luzeraren, zuzenaren puntuen eta zenbaki
errealen artean.Zuzenki eta zenbaki baten biderkadura edo zuzenkien arrazoia,
azkenean, zenbaki errealen biderkadura edo zatidura besterik ez
dira.Zuzenkien luzeren ordez, kurben luzerak, edota areak eta bolumenak
neurtu nahi baldin badira, nahasiagoak izaten dira gauzak.
Antzina, kasu horietan agorbide izeneko metodoa erabiltzen zen.
Alegia, irudi makur baten area aurkitzeko, adibidez, irudi hori
poligono inskribatu eta zirkunskribatuekin alderatzen zen, etahaien area kalkulatzen zen, irudi makurrera gero eta gehiago hurbiltzeko
. Gaur egun, integrazioz ebazten dira era horretako problemak,
objektuaren formatik eta erabili nahi den geometria
metrikoari dagokion luzera, area edo bolumen elementutik abiatuz
. Oinarrizko geometriaren irudiei dagokienez, aski izaten da
hori, irudi horiek ez baitituzte sortzen ezjarraitasun infinituen edo
tasun topologiko zailak dituzten esparruen arazoak; arazo horiek,
hain zuzen ere, ekarri zuten Borel eta Lebesguek garatu zuten neurriaren
teoria orokortzea eta finkatzea, neurria, integrazioa eta
topologia lotuz.
I I. Neurriak eta mundu fisikoa : metroa
Neurriaren arazoa, matematikan, fisikako neurrien arazoekin
dago lotua. Zuzenki idealen neurri abstraktuak ez dute zertan bat
etorririk neurri errealekin, baina, hasteko, onartzen da bat datorrela
espazio fisikoa hiru dimentsioko espazio euklidearrarekin, eta
halaber bat datozela matematika neurriak fisikakoekin.Matematikaren emaitzak fisikari aplikatu ahal izateko, batetik,
neurri banako bat finkatu behar da, eta, bestetik, emaitzak adierazteko
erabiliko den zenbakitze sistema.Metroa da gaur egun erabiltzen den luzeren neurri sistema unibertsala
.Luzera ez da fisikan definitzen den magnitude bakarra ; badira
beste batzuk, masa edo denbora adibidez, beren banako bereziak
dituztenak. Zientzietan erabiltzen den neurri sistemari Nazioarteko
Sistema deritza.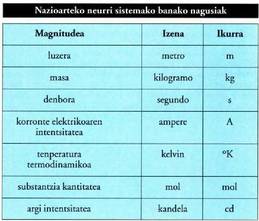 Bigarren auzia da emaitzak banakoetan edo zatiki hamartarretan
adierazten direla. Oso zenbaki handiak edo oso txikiak ez erabiltzearren,
multiploak edo azpimultiplo hamartarrak erabiltzen dira.
Bigarren auzia da emaitzak banakoetan edo zatiki hamartarretan
adierazten direla. Oso zenbaki handiak edo oso txikiak ez erabiltzearren,
multiploak edo azpimultiplo hamartarrak erabiltzen dira.
Hamabikoak edo herenak ez dira neurri gisa erabiltzen Nazioarteko
Sisteman. Banakoaren multiploak edo azpimultiploak aurrizki
jakinen bidez adierazten dira ; ondoko taulan ageri dira aurrizki
horiek :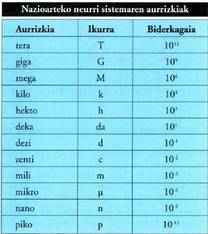 Neurri sistema hamartarraren bilakaeraren emaitza da Nazioarteko
Sistema. Neurri banako horiek Frantziako Iraultzaren garaian
hasi ziren erabiltzen. 1790ean, luzera banako bat proposatzea eskatu
zion Nazio Batzarrak Zientzien Akademiari. Pisu eta Neurri Batzordeak
metroa proposatu zuen, Lurraren meridianoaren laurdenaren
hamar milioiren gisa definitzen zena. Horren balioa zehazteko,
Dunkerquetik Bartzelonara doan meridianoa neurtu zen. Neurketa
horren emaitzarekin, platinozko metro baten eredu bat egin zen
(1799), arau balioa izango zuena, eta urte horretan bertan kaleratu
zen metroa Frantziako neurri ofiziala bihurtzen zuen dekretua. Gaur
egungo kalkuluen arabera, meridiano laurdenak 10.002.288 metro
du, hau da, lehen ereduak baino zertxobait gehiago.Napoleonek osteek eraman zuten metroa atzerrira, baina oso
poliki zabaldu zen. Hasieran, Frantzian, Herbehereetan eta italiar
estatu batzuetan onartu zuten. Baina, zabaldu ahala, soilik frantsesa
izateari utzi zion, eta pisu eta neurrien nazioarteko bulego baten
mende geratu zen ; Sevresen zuen bulego horrek egoitza, Paristik
gertu. Espainian 1892an onartu zen metroa. Bestalde, metroa onartu
zuten herriek ereduaren kopia bat egin zuten.Metroaren lehen eredua 1889an berritu zen, I. Conference
generale des poids et des mesures biltzarrean. Iridio platinozko eredua
0° C izotzetan gordetzen bazen ere, eta behaketa akatsak
txiki-txikiak ziren arren, metro milioiren bat baino gutxiago (10 -
6 ), neurriak zehaztu beharra dela-eta, definizio berri bat erabiltzen
da egun, Lurraren araberakoa ez dena, argi irraden araberakoa
baizik. 1960ko XI. Conferencegenerale des poids et des mesures
batzarrean, metro gisa onartu zen luzera, kripton 86-ren atomoaren
2p,, eta 5d 5 mailen arteko trantsizioari dagokion irradak
espazio hutsean duen uhin luzera 1650763,73 aldiz da. 10 - 'mrainokoa
da prozedura horren bidez lorturiko neurrien zehaztasuna
.1960. urteaz gero, Nazioarteko Sistema deritzan neurri fisikoen
sistema baten baitakoa da metroa. Sistema hori legezkoa da Frantzian
eta Espainian, eta horixe erabiltzen dute mundu osoko zientzialariek
. Aurreko sistemak desagertzen ari dira, eta leku jakin batzuetan
bakarrik erabiltzen dira, gauza jakinetan, nahiz eta
britainiar sistema (iardak, oinak eta librak), oraindik ere garrantzitsua
den herri anglosaxoniarretan, eta Britainia Handiko antzinako
kolonietan.
Neurri sistema hamartarraren bilakaeraren emaitza da Nazioarteko
Sistema. Neurri banako horiek Frantziako Iraultzaren garaian
hasi ziren erabiltzen. 1790ean, luzera banako bat proposatzea eskatu
zion Nazio Batzarrak Zientzien Akademiari. Pisu eta Neurri Batzordeak
metroa proposatu zuen, Lurraren meridianoaren laurdenaren
hamar milioiren gisa definitzen zena. Horren balioa zehazteko,
Dunkerquetik Bartzelonara doan meridianoa neurtu zen. Neurketa
horren emaitzarekin, platinozko metro baten eredu bat egin zen
(1799), arau balioa izango zuena, eta urte horretan bertan kaleratu
zen metroa Frantziako neurri ofiziala bihurtzen zuen dekretua. Gaur
egungo kalkuluen arabera, meridiano laurdenak 10.002.288 metro
du, hau da, lehen ereduak baino zertxobait gehiago.Napoleonek osteek eraman zuten metroa atzerrira, baina oso
poliki zabaldu zen. Hasieran, Frantzian, Herbehereetan eta italiar
estatu batzuetan onartu zuten. Baina, zabaldu ahala, soilik frantsesa
izateari utzi zion, eta pisu eta neurrien nazioarteko bulego baten
mende geratu zen ; Sevresen zuen bulego horrek egoitza, Paristik
gertu. Espainian 1892an onartu zen metroa. Bestalde, metroa onartu
zuten herriek ereduaren kopia bat egin zuten.Metroaren lehen eredua 1889an berritu zen, I. Conference
generale des poids et des mesures biltzarrean. Iridio platinozko eredua
0° C izotzetan gordetzen bazen ere, eta behaketa akatsak
txiki-txikiak ziren arren, metro milioiren bat baino gutxiago (10 -
6 ), neurriak zehaztu beharra dela-eta, definizio berri bat erabiltzen
da egun, Lurraren araberakoa ez dena, argi irraden araberakoa
baizik. 1960ko XI. Conferencegenerale des poids et des mesures
batzarrean, metro gisa onartu zen luzera, kripton 86-ren atomoaren
2p,, eta 5d 5 mailen arteko trantsizioari dagokion irradak
espazio hutsean duen uhin luzera 1650763,73 aldiz da. 10 - 'mrainokoa
da prozedura horren bidez lorturiko neurrien zehaztasuna
.1960. urteaz gero, Nazioarteko Sistema deritzan neurri fisikoen
sistema baten baitakoa da metroa. Sistema hori legezkoa da Frantzian
eta Espainian, eta horixe erabiltzen dute mundu osoko zientzialariek
. Aurreko sistemak desagertzen ari dira, eta leku jakin batzuetan
bakarrik erabiltzen dira, gauza jakinetan, nahiz eta
britainiar sistema (iardak, oinak eta librak), oraindik ere garrantzitsua
den herri anglosaxoniarretan, eta Britainia Handiko antzinako
kolonietan.
Metroaren aurreko neurriak
Sistema metrikoa onartu aurreko neurriak era askotakoak ziren, eta,
horretaz, menderatzen oso zailak. Luzeren neurriak ziren bateratuenak.
Gipuzkoan, Bizkaian eta Araban Gaztelako kana zen banakoa, eta 84
bat cm balio zituen. Hiru oinetan banatzen zen, bakoitzak 28 bat cm
zituela, edo 36 hatzetan, 2,33 cm-koa bakoitza. Arra edo besoa ere erabiltzen
ziren. Nafarroan bestelako banako batzuk erabiltzen ziren, Aragoiko
erreinukoarekin zerikusia zutenak. Iruñeko kanak 79 cm inguru
zen, eta oinak 26,5. Frantzian banako nagusia toise-a zen, sei oin zituena,
eta 1,95 m zituen ; hala, oin frantsesak 33 bat cm zituen. Europako
beste lekuetan ere oso nahasiak ziren gauzak, eta baziren oin erromatarrak, Rhingo oinak, Bruselakoak, Bavariakoak, Londreskoak, Estrasburgokoak,
Veneziakoak eta beste leku askotakoak. Antzinako erromatar
oinak bazuen erreferentzia balioa, baina aski dudazkoa, ez baitzetozen
bat herri guztiak oin horren luzeran.Are nahasiagoak ziren pisu eta gainalde banakoak. Gaztelan libra
zen pisu banakoa ; 460 gr zituen, eta 28,75 gr-ko 16 ontzatan banatzen
zen, baina aldi berean bazen beste libra bat, 12 ontza besterik ez zituena.
Gipuzkoan 492 gr-ko libra erabiltzen zen, gutxi gorabehera 17
ontza zituena; baina 16 zatitan banatzen zuten, eta, hala, gipuzkoar
ontza batek 30,8 gr balio zituen, hau da, Baionako ontzak (31 gr) etaNafarroakoak bezalatsu. Bizkaian librak 488 gr zituen, eta Galizian
berriz 20 ontza eta 575 gramoko libra erabiltzen zen.Horrez gainera, muga lekuetan, Donostian adibidez, merkataritza harreman
asko baitzuen Frantzia eta Nafarroarekin, probintziako gainerako
lekuetako ez bezalako banakoak erabiltzen ziren; gaiaren arabera ere izan
zitezkeen neurri bereziak. Horrek bidegabekeria asko ekartzen zuen, Bilboko
predikari batek XVIII. mendean salatzen zuenez : "Bekatu larria egiten
dure pisu bat erabiltzen dutenek jasotzeko eta erosteko, eta beste bat txikiagoa
eta desleiala emateko". Gauza ziurra da ez zirela Bilboko merkatariak
neurrien areko aldeak beren onurarako erabiltzen zituzten bakarrak.
I I I. Banakoen aldaketa neurri sistema hamartarrean
Banakoak hamarrenetan banatzea da sistema hamartarraren
abantaila nagusietako bat, eta ez heren, hamabiren edo hamaseirenetan,
beste sistemetan gertatzen den bezala. Luzera neurri bat,
banako jakin batean adierazia, hurrengo banako txikiagora bihurtzeko,
aski da ehunez biderkatzea edo koma lekuz aldatzea. Aitzitik,
banako handiagora bihurtu nahi bada, hamarrez zatitzen da, bi
aldiz handiagoa nahi bada, ehunez, etab.Kontuan izan behar da ordea gainalde banakoak luzera bider luzera direla, eta hori dela-eta, ehunka doaz ; bolumen banakoak luzera bider luzera bider luzera, hau da, milaka doaz. Alegia, bolumenaren baten milarena
baten milarena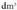 bat da, eta ez
bat da, eta ez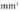 bat. Era berean,
bat. Era berean,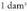 da, eta ez
da, eta ez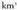 bat.Neurri sisteman oinarritzen diren arren, erabil daitezke arau horri jarraitzen ez dioten gainalde eta bolumenari dagozkion banakoak, ez baitira sistema horretakoak. Horretaz, litroa
bat.Neurri sisteman oinarritzen diren arren, erabil daitezke arau horri jarraitzen ez dioten gainalde eta bolumenari dagozkion banakoak, ez baitira sistema horretakoak. Horretaz, litroa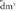 bat da, dezilitroa
bat da, dezilitroa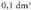 , eta mililitroa 0,001 litro, alegia,
, eta mililitroa 0,001 litro, alegia,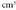 bat.Gauza bera gertatzen da gainaldeetan : area bat
bat.Gauza bera gertatzen da gainaldeetan : area bat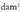 bat da, eta zentiarea bat
bat da, eta zentiarea bat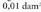 , hots,
, hots,
Ariketak
1. Adieraz itzazu banako hauek metroetan : 2. Alda itzazu metroak ondoren adierazten den banakora :
2. Alda itzazu metroak ondoren adierazten den banakora : 3. Alda itzazu gainalde banako hauek
3. Alda itzazu gainalde banako hauek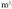 - tara :
- tara :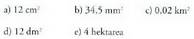 4. Alda itzazu gainalde hauek
4. Alda itzazu gainalde hauek inserted text- tatik ondoren adierazten diren banakoetara :
inserted text- tatik ondoren adierazten diren banakoetara : 5. Alda itzazu bolumen banako hauek
5. Alda itzazu bolumen banako hauek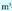 - tara :
- tara : 6.Ondoko bolumen hauek, alda itzazu
6.Ondoko bolumen hauek, alda itzazu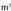 - etatik ondoren adierazten diren banakoetara :
- etatik ondoren adierazten diren banakoetara :
I V. Luzeren kalkulua
Luzera bat kalkulatu nahi bada, zuzenean egin daiteke, tresna egokiak erabiliz, edota zeharka, iristerrazagoak diren edota neurtzen errazak gertatzen diren zuzenkiak neurtuz, eta horretarako egokiak diren erlazio matematikoak erabiliz gero. Luzeren artean, erlaziorik emankorrena Pitagorasen teorema da, planoko irudia horrela hartuz :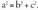 . Edota espazioak hiru norabide ortogonaletan zatituz, hau da,
. Edota espazioak hiru norabide ortogonaletan zatituz, hau da, Angeluen datuak eskura izanez gero, errazagoa izaten da kalkuluak trigonometria bidez egitea, sinuaren eta kosinuaren teoremak erabiliz. Oro har, trigonometriaren baitan ebatzi ohi dira irudi lauetan, edo espazioko irudietan, sortzen diren luzera arazo erraz batzuk, bereziki gainalde eta bolumenekin zerikusia dutenak :Laukiaren aldea jakinda, diagonala aurkitu.Aldea L baldin bada, Pitagorasen teoremaren bidez,
Angeluen datuak eskura izanez gero, errazagoa izaten da kalkuluak trigonometria bidez egitea, sinuaren eta kosinuaren teoremak erabiliz. Oro har, trigonometriaren baitan ebatzi ohi dira irudi lauetan, edo espazioko irudietan, sortzen diren luzera arazo erraz batzuk, bereziki gainalde eta bolumenekin zerikusia dutenak :Laukiaren aldea jakinda, diagonala aurkitu.Aldea L baldin bada, Pitagorasen teoremaren bidez,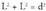 Beraz,
Beraz,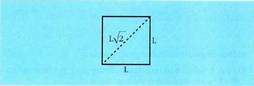 Triangelu aldekide baten aldea jakinda, triangelu horren altura,
zirkunskribaturiko zirkunferentziaren erradioa (R) eta inskribaturiko
r-arena aurkitu.Aldea L bada, triangelu aldekidean altura, erdibitzailea eta erdibidekoa berdin direlako, erpinetik alturak oina ebakitzen duen punturainoko distantzia L/2 izango da ; Pitagorasen teoremaren arabera,
Triangelu aldekide baten aldea jakinda, triangelu horren altura,
zirkunskribaturiko zirkunferentziaren erradioa (R) eta inskribaturiko
r-arena aurkitu.Aldea L bada, triangelu aldekidean altura, erdibitzailea eta erdibidekoa berdin direlako, erpinetik alturak oina ebakitzen duen punturainoko distantzia L/2 izango da ; Pitagorasen teoremaren arabera, , beraz
, beraz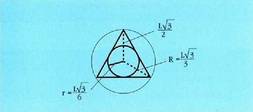 zirkunferentzia zirkunskribatuaren erradioa, garaierekin eta erdibitzaileekin bat datozen erdibidekoak erpinetik bi herenetara elkar ebakitzen dutelako, hau izango da :
zirkunferentzia zirkunskribatuaren erradioa, garaierekin eta erdibitzaileekin bat datozen erdibidekoak erpinetik bi herenetara elkar ebakitzen dutelako, hau izango da :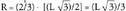 Arrazoibide bera erabiliz, zirkunferentzia inskribatuaren erradioa hau izango da :
Arrazoibide bera erabiliz, zirkunferentzia inskribatuaren erradioa hau izango da :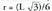 Aldea jakinda, poligono erregular baten apotema eta erradioa
aurkitu, hau da, zirkunferentzia inskribatuaren eta zirkunskribatuaren
erradioa.Aldea L baldin bada, eta n aldeen kopurua, angelu guztien batura
Aldea jakinda, poligono erregular baten apotema eta erradioa
aurkitu, hau da, zirkunferentzia inskribatuaren eta zirkunskribatuaren
erradioa.Aldea L baldin bada, eta n aldeen kopurua, angelu guztien batura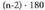 da, beraz, barneko angeluaren balioa ere badakigu. Poligonoatriangeluetan zatitzen bada, erpinak zentroarekin lotuz, erradioa bat etorriko da bi alde berdinekin eta apotema altura izango da.
da, beraz, barneko angeluaren balioa ere badakigu. Poligonoatriangeluetan zatitzen bada, erpinak zentroarekin lotuz, erradioa bat etorriko da bi alde berdinekin eta apotema altura izango da.
Alde desberdina ezaguna da, poligonoaren aldea baita. A baldin bada barne angelua, triangeluaren alde berdinak A/2 izango dira, eta eskaturiko distantziak trigonometria bidez lor daitezke :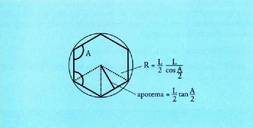 Aldeen diagonala eta kuboaren diagonala.
Aldeen diagonala eta kuboaren diagonala.
Kuboak L baldin badu ertz luzera, Pitagorasen teoremaren bitartez,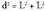 ; alboko diagonalarentzat:
; alboko diagonalarentzat: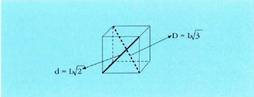 diagonal orokorrarentzat,
diagonal orokorrarentzat,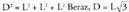 Ortoedro baten diagonalak. Aldeak a, b, c luzerakoak dituen ortoedro batek, hau du a eta b-k mugaturiko aldearen diagonala :
Ortoedro baten diagonalak. Aldeak a, b, c luzerakoak dituen ortoedro batek, hau du a eta b-k mugaturiko aldearen diagonala :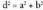 eta diagonal orokorra berriz,
eta diagonal orokorra berriz,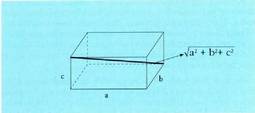 Tetraedro erregular baten altura.Aldea L duen tetraedro erregular batean, aldeen apotema triangelu aldekideen altura da, eta, hortaz,
Tetraedro erregular baten altura.Aldea L duen tetraedro erregular batean, aldeen apotema triangelu aldekideen altura da, eta, hortaz,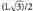 du balioa. Tetraedro erregularraren altura, erpinetik erpin horrek oinarrian duen proiekziora doan distantzia da. Proiekzio hori, piramidea erregularra delako, eta oinarria triangelu aldekide bat duelako, triangelu horren erdibitzailean egongo da, erpinetik bi herenetara, eta aldearen heren batera. Oinarriarekiko ebaki zut bat eginez, erpinetik eta kontrako ertzaren erditik, hau lortzen da :
du balioa. Tetraedro erregularraren altura, erpinetik erpin horrek oinarrian duen proiekziora doan distantzia da. Proiekzio hori, piramidea erregularra delako, eta oinarria triangelu aldekide bat duelako, triangelu horren erdibitzailean egongo da, erpinetik bi herenetara, eta aldearen heren batera. Oinarriarekiko ebaki zut bat eginez, erpinetik eta kontrako ertzaren erditik, hau lortzen da : Piramide erregular batean, edozein delarik ere, beti gertatzen da
alboko ertza ber bi, berdin oinarria zirkunskribatzen duen zirkunferentziaren erradioa ber bi, gehi piramidearen altura ber bi dela. Eta piramidearen apotema ber bi, berdin oinarriko poligonoaren apotema ber bi, gehi piramidearen altura ber bi dela.
Piramide erregular batean, edozein delarik ere, beti gertatzen da
alboko ertza ber bi, berdin oinarria zirkunskribatzen duen zirkunferentziaren erradioa ber bi, gehi piramidearen altura ber bi dela. Eta piramidearen apotema ber bi, berdin oinarriko poligonoaren apotema ber bi, gehi piramidearen altura ber bi dela.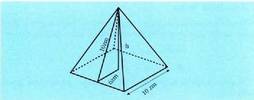 Kono zuzen batean, beti gertatzen da sortzailea ber bi, berdin oinarriaren erradioa ber bi gehi altura ber bi dela:
Kono zuzen batean, beti gertatzen da sortzailea ber bi, berdin oinarriaren erradioa ber bi gehi altura ber bi dela: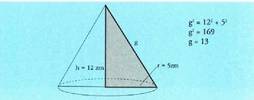 Esfera bat plano batez ebakitzen bada zentrotik R erradioa baino d distantzia laburrago batera, epaia zirkunferentzia bat izango da, erradioa r izango duena, era honetara :
Esfera bat plano batez ebakitzen bada zentrotik R erradioa baino d distantzia laburrago batera, epaia zirkunferentzia bat izango da, erradioa r izango duena, era honetara :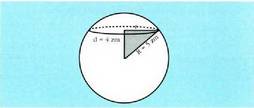 Poligono baten perimetroak.Poligono baten perimetro aldeen luzeren baturari esaten zaio.
Poligono baten perimetroak.Poligono baten perimetro aldeen luzeren baturari esaten zaio.
Poligono erregularra baldin bada, erraza da kalkulatzen, zeren n
aldetako eta L luzerako poligono erregular batek, hau du perimetroa :
- Ariketak
7. Marrazkiko kuboan, ertzaren luzera a izanik, aurki
izatzu EM, MG eta EG.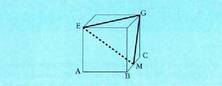 8. L aldea duen kubo batean, froga ezazu hexagono erregular
bat dela ertzen erdiko puntuak lotuz lortzen den irudia,
eta DF diagonalaren erdibitzailea dela bere planoa.
8. L aldea duen kubo batean, froga ezazu hexagono erregular
bat dela ertzen erdiko puntuak lotuz lortzen den irudia,
eta DF diagonalaren erdibitzailea dela bere planoa.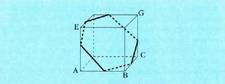 9. Froga ezazu hexaedro edo kubo baten sei aurpegiak
elkarrekin lotuz lortzen den poliedroa oktaedro erregularra
dela.
9. Froga ezazu hexaedro edo kubo baten sei aurpegiak
elkarrekin lotuz lortzen den poliedroa oktaedro erregularra
dela.
V. Zirkunferentziaren luzera
Poligonoen definizioaren hedaduraz, perimetro deritza zirkunferentziaren
luzera osoari.Antzina-antzinatik dakigu zirkuluaren luzera eta diametroa zuzenki proportzionalak direla. Eulerrez gero, deritza arrazoi horren zenbaki balioari, perimetroaren izen grekoaren
deritza arrazoi horren zenbaki balioari, perimetroaren izen grekoaren lehen letratik datorren hitza erabiliz.Konstante horren balioaren arabera, hau da zirkunferentziaren
balioa :
lehen letratik datorren hitza erabiliz.Konstante horren balioaren arabera, hau da zirkunferentziaren
balioa :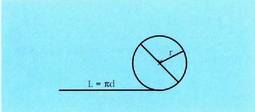 Antzina-antzinatik datorren arazoa da
Antzina-antzinatik datorren arazoa da konstantearen balioa jakin nahia. Horretarako, bi bide erabili izan dira: balio errealari hurbiltzea ahalbidetuko duten metodoak aurkitzea, edo balio zehatza emango duen kalkuluren bat aurkitzea. Lehen sistemak bide luzea egin du Ahmes papiroaz gero (K.a. XVII. mendea;
konstantearen balioa jakin nahia. Horretarako, bi bide erabili izan dira: balio errealari hurbiltzea ahalbidetuko duten metodoak aurkitzea, edo balio zehatza emango duen kalkuluren bat aurkitzea. Lehen sistemak bide luzea egin du Ahmes papiroaz gero (K.a. XVII. mendea; balioa ematen zion papiro horrek
balioa ematen zion papiro horrek - ri ), gure egunak arte ; orain, ordenagailu eta algoritmo ahaltsuen bidez,
- ri ), gure egunak arte ; orain, ordenagailu eta algoritmo ahaltsuen bidez, - ren berrogeita hamaika mila milioi hamarren zehatz aurkitu dira. Bigarren bidea,
- ren berrogeita hamaika mila milioi hamarren zehatz aurkitu dira. Bigarren bidea, - ren balioa kalkulatzeko modu zehatz bat aurkitzea, zirkuluaren koadraturaren problema da, hau da, zirkulu jakin baten area berdina duen karratu baten aldea aurkitzea, zeren L karratuaren aldearen balioa ezagutzen bada, zirkuluaren r erradioa
- ren balioa kalkulatzeko modu zehatz bat aurkitzea, zirkuluaren koadraturaren problema da, hau da, zirkulu jakin baten area berdina duen karratu baten aldea aurkitzea, zeren L karratuaren aldearen balioa ezagutzen bada, zirkuluaren r erradioa izango baita. Bide hori dela-eta, aspalditik zegoen susmoa ez zuela irtenbiderik.
izango baita. Bide hori dela-eta, aspalditik zegoen susmoa ez zuela irtenbiderik. jakiteko aurkitu ziren formak, antzina, kurba mekanikoak izan ziren, eta, gero, XVII. eta XVIII. mendeetan, segida infinituak edo funtzio transzendenteak. 1882an E.Lindemannek frogatu zuen
jakiteko aurkitu ziren formak, antzina, kurba mekanikoak izan ziren, eta, gero, XVII. eta XVIII. mendeetan, segida infinituak edo funtzio transzendenteak. 1882an E.Lindemannek frogatu zuen
Arku baten luzera
Dagokion angeluaren balioa ezaguna baldin bada, a gradu edo A
radian, arku baten luzera hiruko erregelaren bidez kalkulatzen da : Angelua radianetan emana baldin badago, adierazpena guztiz
erraza da :
Angelua radianetan emana baldin badago, adierazpena guztiz
erraza da :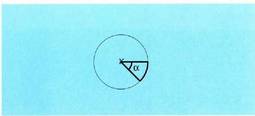 Beraz,
Beraz,
- Ariketa
10. Gurdi batek 1 m-ko diametroko gurpil bat du. Milioi bat itzuli egin ondoren, zenbat kilometro egin ditu?
Zirkuluaren koadratura eta n zenbakia
Zirkuluaren koadraturaren problema, kuboaren bikoiztearen eta angeluaren
trisekzioaren ondoan, matematika grekoko irtenbiderik gabeko
problema klasikoetako bat zen. Euklidesek, jadanik Elementuak liburuko
XII. liburuko bigarren perpausean, frogatu zuen "zirkulu bat beste batekiko
haren diametroa ber bi bestearena ber bi adina" dela, eta Arkimedesek
berriz zirkunferentziaren luzera aurkitzearen problemara laburtu zuen.
Baina ez zen ezagutzen zirkunferentziaren eta diametroaren arteko arrazoiaren
balioa, ezta zehaztasunez aurkitzeko modurik ere. Grekoek aurkitu
zuten horren balioa aurkitzeko bide bat, kurba mekanikoak erabiliz ;
hau da, mugimendu bat erabiliz definitzen ziren kurbak. Horietako bat
koadratriza edo trisektriza erabiltzea zen ; uniformeki biratzen duen erradio
baten eta lastertasun uniformez jaisten den zuzen baten arteko ebakidura
puntuak aurkituz lortzen da ; bi horien mugimendua batera hasten da
zirkuluaren goreneko D puntuan, era halako lastertasunez mugitzen dira,
non aldi berean heltzen baitira AB erradio horizontalera. Kasu honetan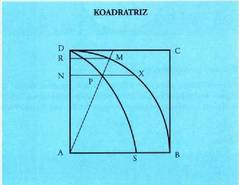 Baina S puntuaren definizioa ez da ebakidura batetik sortzen, limite bat
eginez baizik. Bestalde, greziar geometrian ez ziren ontzat hartzen mugimendua
behar zuten ebazpideak.Arkimedesen espirala da grekoek
erabiltzen zuten beste
kurba bat, honela definitzen
dena : erradio baten gainean
dagoen puntu baten ibilbidea
da, eta zentrotik lastertasun uniformez
aldentzen dena, kokaturik
dagoen erradioa lastertasun
angeluar uniformez biratzen den
artean. Arkimedesek frogatua
zeukan hau : 18. Zuzen barek
lehen biraren ertzean ukitzen
badu espirala, eta jatorritik biraren
jatorrizko zuzenarekiko
zuzen zut bat marrazten baldin
bada, lerro zut horrek ukitzailea
ebakiko du, eta ukitzailearen eta
espiralaren jatorriaren artean
geratzen den parrea lehen zirkuluaren
berdina izango da'. Hau
da :
Baina S puntuaren definizioa ez da ebakidura batetik sortzen, limite bat
eginez baizik. Bestalde, greziar geometrian ez ziren ontzat hartzen mugimendua
behar zuten ebazpideak.Arkimedesen espirala da grekoek
erabiltzen zuten beste
kurba bat, honela definitzen
dena : erradio baten gainean
dagoen puntu baten ibilbidea
da, eta zentrotik lastertasun uniformez
aldentzen dena, kokaturik
dagoen erradioa lastertasun
angeluar uniformez biratzen den
artean. Arkimedesek frogatua
zeukan hau : 18. Zuzen barek
lehen biraren ertzean ukitzen
badu espirala, eta jatorritik biraren
jatorrizko zuzenarekiko
zuzen zut bat marrazten baldin
bada, lerro zut horrek ukitzailea
ebakiko du, eta ukitzailearen eta
espiralaren jatorriaren artean
geratzen den parrea lehen zirkuluaren
berdina izango da'. Hau
da :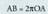 Baina hori ere kurba mekanikoa zen.Geroago aurkitu ziren metodoak ere ez ziren hobeak. Izan ziren porrot famatu batzuk, hala Hobbes filisofoarena adibidez, 1669an. Baina, Berpizkundeaz gero, arazoa aztertu zuten matematikariek aurkitu zituzten
Baina hori ere kurba mekanikoa zen.Geroago aurkitu ziren metodoak ere ez ziren hobeak. Izan ziren porrot famatu batzuk, hala Hobbes filisofoarena adibidez, 1669an. Baina, Berpizkundeaz gero, arazoa aztertu zuten matematikariek aurkitu zituzten ematen zuten adierazpenak batuketa edo biderkadura infinitu baten emaitza gisa, eta uste zen ezin zitekeela soluzio zehatzagorik izan. 1776an Lambertek frogatu zuen
ematen zuten adierazpenak batuketa edo biderkadura infinitu baten emaitza gisa, eta uste zen ezin zitekeela soluzio zehatzagorik izan. 1776an Lambertek frogatu zuen irrazionala behar zuela izan, eta azkenik 1 882an F. Lindemannek frogatu zuen
irrazionala behar zuela izan, eta azkenik 1 882an F. Lindemannek frogatu zuen transzendentea dela, eta ezin duela beraz izan ekuazio polinomiko baten ebazpena, hau da, ezin daiteke aurkitu erregela eta konpasa erabiliz, ezta konikoekin edo polinomioen arrazoi diren beste kurbekin ere. Hortaz, ezin da zirkuluaren koadratura egin, antzina esaten zen bezala. Bestelakoa da hurbileko soluzioen historia, emaitzak etengabe hobetu baitira. Ezagutzen den hurbilpen zaharrena Ahmesen papiroan ageri dena da, K.a. 1650. urtean kopiatu zuen eskribauaren izenaren omenez izendatu dena horrela ; Rhindena ere esaten zaio, joan den mendean papiroa erosi zuen ingelesaren omenez. 50. problemak dioenez, diametroko 9 banako dituen eremu zirkular baten area, aldeko 8 banako dituen lauki baten arearen berdina da. Horren ondorioz,
transzendentea dela, eta ezin duela beraz izan ekuazio polinomiko baten ebazpena, hau da, ezin daiteke aurkitu erregela eta konpasa erabiliz, ezta konikoekin edo polinomioen arrazoi diren beste kurbekin ere. Hortaz, ezin da zirkuluaren koadratura egin, antzina esaten zen bezala. Bestelakoa da hurbileko soluzioen historia, emaitzak etengabe hobetu baitira. Ezagutzen den hurbilpen zaharrena Ahmesen papiroan ageri dena da, K.a. 1650. urtean kopiatu zuen eskribauaren izenaren omenez izendatu dena horrela ; Rhindena ere esaten zaio, joan den mendean papiroa erosi zuen ingelesaren omenez. 50. problemak dioenez, diametroko 9 banako dituen eremu zirkular baten area, aldeko 8 banako dituen lauki baten arearen berdina da. Horren ondorioz, , beraz,
, beraz, . Luzaroan gehien erabili zen balioa Arkimedesek aurkitu zuen, K.a. II. mendean ; poligono inskribatuak eta zirkunskribatuak zituen zirkulu bat oinarri hartuta, hau proposatzen zuen :
. Luzaroan gehien erabili zen balioa Arkimedesek aurkitu zuen, K.a. II. mendean ; poligono inskribatuak eta zirkunskribatuak zituen zirkulu bat oinarri hartuta, hau proposatzen zuen :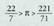 Eta hor 22/7 = 3,1428... Gure aroko V. mendean Tsu Ch'ung-Chih txinatar astronomoak 355/113 (3,1415929...) balioa aurkitu zuen, are hobea dena; Herbehereetako matematikari batek, Adrian Menciok, berriro aurkitu zuen XVI. mendearen bukaeran. Hurbileko emaitzarik hoberena, gero eta alde gehiago zituzten poligonoak inskribatuz lortua, jatorriz Koloniakoa zen baina Holandan bizi eta lan egin zuen matematikari batek lortu zuen, Ludolph Van Ceulenek ; hark, XVII. mendearen hasieran,
Eta hor 22/7 = 3,1428... Gure aroko V. mendean Tsu Ch'ung-Chih txinatar astronomoak 355/113 (3,1415929...) balioa aurkitu zuen, are hobea dena; Herbehereetako matematikari batek, Adrian Menciok, berriro aurkitu zuen XVI. mendearen bukaeran. Hurbileko emaitzarik hoberena, gero eta alde gehiago zituzten poligonoak inskribatuz lortua, jatorriz Koloniakoa zen baina Holandan bizi eta lan egin zuen matematikari batek lortu zuen, Ludolph Van Ceulenek ; hark, XVII. mendearen hasieran, - ren 35 hamarren aurkitu zituen :3,14159265358979323846264338327950288Hurbileko emaitza honen ondoren, matematikariek pentsatu zuten
- ren 35 hamarren aurkitu zituen :3,14159265358979323846264338327950288Hurbileko emaitza honen ondoren, matematikariek pentsatu zuten - ren baliora lasterrago hurbilduko ziren metodoak aurkitu behar zirela, eta hainbat metodo interesgarri aurkitu ziren. XVII. mendearen erdialdean Wallis matematikari ingelesak, Hobbesen koadratura faltsua kritikatu ondoren, hau aurkitu zuen :
- ren baliora lasterrago hurbilduko ziren metodoak aurkitu behar zirela, eta hainbat metodo interesgarri aurkitu ziren. XVII. mendearen erdialdean Wallis matematikari ingelesak, Hobbesen koadratura faltsua kritikatu ondoren, hau aurkitu zuen : Lcihniz filosofo eta matematikari famatuak hau proposatu zuen XVII.. endean :
Lcihniz filosofo eta matematikari famatuak hau proposatu zuen XVII.. endean :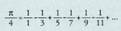 Taylorren funtzioen segidako garapenaren aurkikuntzarekin, XVIII.. endean asko ugaritu ziren hurbileko balioak aurkitzeko formulak. Ohikoenak
arku tangenteen segida baten garapenean oinarritzen ziren (ukitzaileak
x balio duen arkua) :
Taylorren funtzioen segidako garapenaren aurkikuntzarekin, XVIII.. endean asko ugaritu ziren hurbileko balioak aurkitzeko formulak. Ohikoenak
arku tangenteen segida baten garapenean oinarritzen ziren (ukitzaileak
x balio duen arkua) : Segida oso poliki bateratzen denez gero, oso nekeza da hurbilpen on batera iristea, eta horregatik erabiltzen dira x-en balioak 1 baino txikiagoak, eta orobat
Segida oso poliki bateratzen denez gero, oso nekeza da hurbilpen on batera iristea, eta horregatik erabiltzen dira x-en balioak 1 baino txikiagoak, eta orobat hainbat arkuren batura gisa aurkitzea ahalbidetzen duten formulak, adibidez :
hainbat arkuren batura gisa aurkitzea ahalbidetzen duten formulak, adibidez :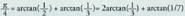 Gaur egun, ordenagailua erabiliz,
Gaur egun, ordenagailua erabiliz, zenbakiaren hamarrenak kalkulatzea
ez da batere gauza zaila. 1960an baziren ehundaka mila hamarren
zehatz, eta 1997an badira milaka milioi.
zenbakiaren hamarrenak kalkulatzea
ez da batere gauza zaila. 1960an baziren ehundaka mila hamarren
zehatz, eta 1997an badira milaka milioi.
VI. Irudi lauen areak
Gainalde banakoa lauki bat da, alde gisa luzera banako bat duena.
Aldeko 1 banako duen lauki baten area aurkitzeko :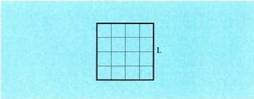 Lauki zuzena.Oinarria b eta altura a dituen lauki zuzen baten area hau da :
Lauki zuzena.Oinarria b eta altura a dituen lauki zuzen baten area hau da :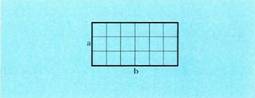 Paralelogramoa.Luzera 1 duen alde bat duen paralelogramo batean, aldeen arteko
distantzia h bada, hau izango da area :
Paralelogramoa.Luzera 1 duen alde bat duen paralelogramo batean, aldeen arteko
distantzia h bada, hau izango da area :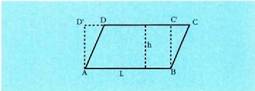 Aski da altura erpinetik marraztea, eta horrela ikusten da ABCD paralelogramoa
Aski da altura erpinetik marraztea, eta horrela ikusten da ABCD paralelogramoa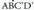 angelu zuzenaren berdina dela, zeren falta den triangelua beste aldean sobran dagoenaren berdina baita.Triangeluak.Oinarria 1 eta altura h duen triangelu batean, area hau da :
angelu zuzenaren berdina dela, zeren falta den triangelua beste aldean sobran dagoenaren berdina baita.Triangeluak.Oinarria 1 eta altura h duen triangelu batean, area hau da :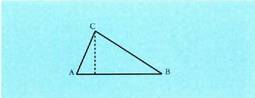 zeren aurkako erpinetik oinarriaren paraleloa, eta beste aldeetako baten paraleloa marrazten badira, area
zeren aurkako erpinetik oinarriaren paraleloa, eta beste aldeetako baten paraleloa marrazten badira, area duen lauki zuzen bat lortzen baita, diagonalak hasieran emandakoaren bi triangelu berdinetan zatitzen duena, eta hortik formula hau :
duen lauki zuzen bat lortzen baita, diagonalak hasieran emandakoaren bi triangelu berdinetan zatitzen duena, eta hortik formula hau :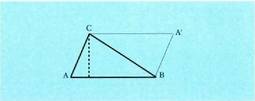 Triangeluen area aurkitzeko Heronen formula.Triangeluaren altura aurkitzea zailagoa izan daiteke aldeak jakitea
baino, eta horregatik beste formula hau ere erabil daiteke :
Triangeluen area aurkitzeko Heronen formula.Triangeluaren altura aurkitzea zailagoa izan daiteke aldeak jakitea
baino, eta horregatik beste formula hau ere erabil daiteke :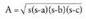 s perimetroerdia delarik, eta a, b eta c, aldeen luzera.
s perimetroerdia delarik, eta a, b eta c, aldeen luzera.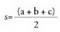 Erronboaren area.Erronboa paralelogramotzat har daiteke, edota horren ordez diagonalak
elkarzutak direlakoaz baliatu, erronboa bi triangelu berdinetan
zatitzen baitute diagonalek. Diagonalek D eta d balio badute,
hau izango da horietako bakoitzaren area :
Erronboaren area.Erronboa paralelogramotzat har daiteke, edota horren ordez diagonalak
elkarzutak direlakoaz baliatu, erronboa bi triangelu berdinetan
zatitzen baitute diagonalek. Diagonalek D eta d balio badute,
hau izango da horietako bakoitzaren area :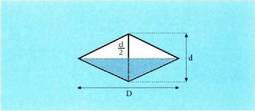 Bi triangelu direnez gero :
Bi triangelu direnez gero :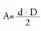 Trapezioaren area.Paralelo ez diren alde baten erdiko puntutik bestearekiko paralelo
bat marrazten bada, lortzen den paralelogramoak trapezioaren
area berdina izango du, zeren kentzen den triangelua batutzen
denaren berdina baita.
Trapezioaren area.Paralelo ez diren alde baten erdiko puntutik bestearekiko paralelo
bat marrazten bada, lortzen den paralelogramoak trapezioaren
area berdina izango du, zeren kentzen den triangelua batutzen
denaren berdina baita.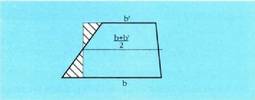 Paralelogramo honen oinarria erdiko paraleloaren luzera da, bi
oinarrien baturaerdia balio duena, beraz, area hau da :
Paralelogramo honen oinarria erdiko paraleloaren luzera da, bi
oinarrien baturaerdia balio duena, beraz, area hau da :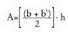 h altura edo alde paraleloen arteko distantzia izanik.Laukiak oro har eta edozein poligono.Orokorrean, ez da formula jakinik edozein poligonotarako.
h altura edo alde paraleloen arteko distantzia izanik.Laukiak oro har eta edozein poligono.Orokorrean, ez da formula jakinik edozein poligonotarako.
Metodo orokorrena triangeluetan zatitzea da. Triangeluaren area
ezaguna denez gero, eta edozein poligono triangeluetan zatitu baitaiteke
diagonalak erabiliz, forma horren bidez edozein poligonoren
area aurki daiteke, ezagutzen badira aldeak, eta behar beste diagonal
edo poligonoa zatitu den triangeluen behar beste altura.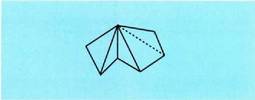 Pentagonoak eta beste poligono erregular batzuk.Poligono erregularretan, bada zentro bat zirkunferentzia zirkunskribatuaren
zentroarekin bat datorrena. Zentro horretatik erpinetara
zuzenak marrazten badira, poligono erregularra triangelu isoszele
berdinetan zatikatzen da ; triangelu horiek poligono erregularraren
aldea dute oinarritzat, eta altura gisa poligonoaren apotema, hau da,
zentrotik alderainoko distantzia. Area beraz hau da :
Pentagonoak eta beste poligono erregular batzuk.Poligono erregularretan, bada zentro bat zirkunferentzia zirkunskribatuaren
zentroarekin bat datorrena. Zentro horretatik erpinetara
zuzenak marrazten badira, poligono erregularra triangelu isoszele
berdinetan zatikatzen da ; triangelu horiek poligono erregularraren
aldea dute oinarritzat, eta altura gisa poligonoaren apotema, hau da,
zentrotik alderainoko distantzia. Area beraz hau da :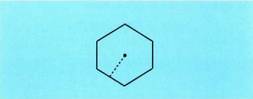 Poligono erregularren barne angelua ezagutzen denez gero, apotema
erraz aurki daiteke trigonometria bidez.Hala adibidez, triangelu aldekidean, apotema
Poligono erregularren barne angelua ezagutzen denez gero, apotema
erraz aurki daiteke trigonometria bidez.Hala adibidez, triangelu aldekidean, apotema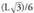 baitu, hau gertatzen da :
baitu, hau gertatzen da :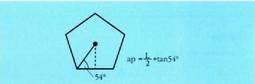 Laukian, apotema L/2 da, beraz :
Laukian, apotema L/2 da, beraz :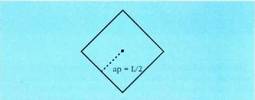 Pentagonoan, apotema (L/2)tan54° da, beraz :
Pentagonoan, apotema (L/2)tan54° da, beraz :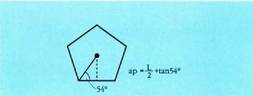 Hexagonoan, apotema
Hexagonoan, apotema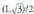 da, beraz
da, beraz
- Ariketa
11.. Poligonono erregular hauetan, denek perimetro bera dutela, esan ezazu zeinek duen area handiena: triangeluak,laukiak ala hexagonoak.
Zirkulua
Zirkuluaren area hau da :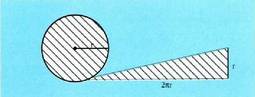 Hori froga daiteke poligono erregularren limite baten bidez, edo,
Euklidesek egin zuen bezala, agorbidezko metodoa erabiliz, hori
azken finean absurdura eramatea baita, limitea erabili ordez. Zirkulu
laurden bat geometria analitikoan ezartzea da ordea biderik errazena.Zirkulu sektorea.Dagokion angeluaren balioa ezagutzen denean (A radian), zirkulu
Hori froga daiteke poligono erregularren limite baten bidez, edo,
Euklidesek egin zuen bezala, agorbidezko metodoa erabiliz, hori
azken finean absurdura eramatea baita, limitea erabili ordez. Zirkulu
laurden bat geometria analitikoan ezartzea da ordea biderik errazena.Zirkulu sektorea.Dagokion angeluaren balioa ezagutzen denean (A radian), zirkulu Eta, horren ondorioz, zirkulu sektore baten gainaldea hau izango da :
Eta, horren ondorioz, zirkulu sektore baten gainaldea hau izango da :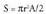 Zirkulu segmentuaren area sektorea ken triangelua izango da, hauda, A radianeko angelu zentralari badagokio, hau egiaztatuko da :
Zirkulu segmentuaren area sektorea ken triangelua izango da, hauda, A radianeko angelu zentralari badagokio, hau egiaztatuko da :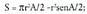 Izan ere, trigonometria bidez, badakigu triangeluaren altura, oinarritzat erradioetako bat hartuta, hau dela :
Izan ere, trigonometria bidez, badakigu triangeluaren altura, oinarritzat erradioetako bat hartuta, hau dela :Zirkulu koroa.Zirkulu koroaren area kanpoko zirkuluaren area ken barrukoarena da:
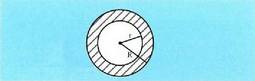 Bien areak, hurrenez hurren, R eta r baldin badira,
Bien areak, hurrenez hurren, R eta r baldin badira,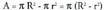 Elipsea.
Elipsea.
Matematikan aurki daitekeen beste irudi biribil-antzeko bat elipsea da, kono baten epaiaren bidez lor daitekeen irudietako bat dena.. eta b ardatzerdiko elipse bat baldin badugu, area hau izango da :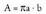 Area hori lortzeko biderik errazena integrazioa da.
Area hori lortzeko biderik errazena integrazioa da.
- Ariketak
12. Kalkula ezazu irudi marradunaren area :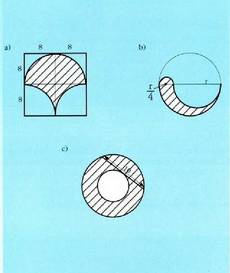 13. Bi banakoko erradioko zirkulu batean, kalkula itzazu
90°-ko angelu zentral bati dagokion zirkulu segmentu
batean area eta perimetroa.
13. Bi banakoko erradioko zirkulu batean, kalkula itzazu
90°-ko angelu zentral bati dagokion zirkulu segmentu
batean area eta perimetroa.
Kioseko Hipokratesen lunulak
Lunulak zirkuluerdiek eta zirkulu segmentuek mugaturiko irudiak
dira. Zehaztasunez "karratu" ziren lehen irudi makurrak izatetik datorkie
ospea ; hau da, lunulei aurkitu zitzaien aurrenekoz area bereko poligonoa.Kioseko Hipokrates K.a. V mendean bizi izan zen, eta ez du batere zerikusirik
Koseko Hipokrates sendagilearekin. Iritsi zaizkigun albisteen arabera,
merkatari gisa hasi zen lanean, baina ez zuen arrakastarik izan, eta
Atenasen geratu zen. Han zaletu zen matematikekin. Ez dakigu eskolakopitagorikoko kide izan ote zen, baina badirudi baduela eskola horren eraginik.Hipokratesek, haren testuak aztertu dituztenen arabera, lunula batbaino gehiago itzuli zuen karratura. Horietan ezagunena zirkuluerdi batekosatua da, horri, kordatzat zirkuluerdi horren berorren diametroa duen
segmentu bat kentzen zaiola, segmentu hori bat datorrelarik halako erradioazentral bati baitagokio.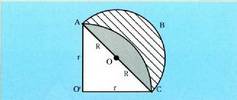 Baldintza horietan, lunularen area zirkuluerdiaren area ken segmentuaren
area da, segmentu horren area, bere aldetik, sektorearen area ken triangeluarena
delarik :
Baldintza horietan, lunularen area zirkuluerdiaren area ken segmentuaren
area da, segmentu horren area, bere aldetik, sektorearen area ken triangeluarena
delarik :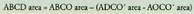 Baina zirkuluerdiaren erradioa R baldin bada,
Baina zirkuluerdiaren erradioa R baldin bada,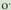 zentroko zirkuluarena r izango da, eta
zentroko zirkuluarena r izango da, eta ko arkua 90°koa denez gero, hau beteko da :
ko arkua 90°koa denez gero, hau beteko da : beraz, sinplifikatuz,
beraz, sinplifikatuz,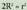 Hau da,
Hau da,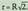 Horrez gainera, ABCO 90°ko angelu sektorea da, hortaz, horren area, zirkuluaren 1/4 izango da. Beraz :
Horrez gainera, ABCO 90°ko angelu sektorea da, hortaz, horren area, zirkuluaren 1/4 izango da. Beraz :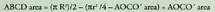 Baina
Baina 2R oinarria eta R altura duen triangelua da, beraz :
2R oinarria eta R altura duen triangelua da, beraz :
VII. Espazioko gorputzen areak eta bolumenak
Poliedro baten area bere aurpegi guztien areen batura da, eta
poliedroa planoan zabaltzeak asko errazten du arearen kalkulua.
Aurpegiak oro har desberdinak izaten dira, eta kalkulua banakabanaka
egin behar da. Baina poliedro erregularretan errazagoa izaten
da kalkulua, aski baita ertzaren balioa jakitea :Tetraedro erregularrak lau alde ditu, triangelu aldekideak. Ertzaren
luzera L baldin bada, hau izango da aurpegiaren area :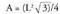 Lau aurpegi berdinen batuketa eginez :
Lau aurpegi berdinen batuketa eginez :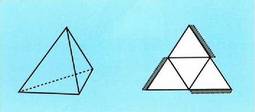 KuboarentzatAurpegi batean areak, ertza 1 baldin bada, A = L- balio du.Beraz, albo area guztira,
KuboarentzatAurpegi batean areak, ertza 1 baldin bada, A = L- balio du.Beraz, albo area guztira,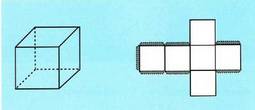 L ertzeko oktaedroan, aurpegiaren area hau da :
L ertzeko oktaedroan, aurpegiaren area hau da :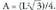 . Beraz, area osoa,
. Beraz, area osoa,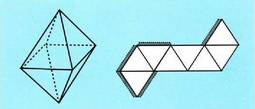 Dodekaedroaren aurpegiak pentagonoak direnez gero, albo area hau da:
Dodekaedroaren aurpegiak pentagonoak direnez gero, albo area hau da: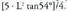 Area osoa beraz :
Area osoa beraz :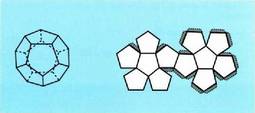 Azkenik, ikosaedroan, aurpegiaren area hau da
Azkenik, ikosaedroan, aurpegiaren area hau da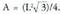 Hogei aurpegi dituenez, area osoa :
Hogei aurpegi dituenez, area osoa :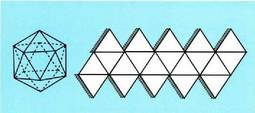 Prismetan, bereizi ohi dira albo area (sortzaileak eratua), eta oinarriaren
area. Prisma zuzen batean, albo area oinarriaren perimetroa
bider ertz zuta da. Area osoa lortzeko, bi bider batu behar da oinarri
baten area, bi oinarriak berdinak baitira.
Prismetan, bereizi ohi dira albo area (sortzaileak eratua), eta oinarriaren
area. Prisma zuzen batean, albo area oinarriaren perimetroa
bider ertz zuta da. Area osoa lortzeko, bi bider batu behar da oinarri
baten area, bi oinarriak berdinak baitira.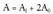 Ortoedroaren kasuan, ertzak a, b eta c dira, eta aurpegi bakoitza
lauki zuzena, beraz :
Ortoedroaren kasuan, ertzak a, b eta c dira, eta aurpegi bakoitza
lauki zuzena, beraz :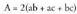 Piramideetan, area osoa albo triangeluen area gehi oinarriarena
da. Piramidea erregularra baldin bada, alboetako triangeluak isoszeleak
izango dira, triangelu horien oinarria piramidearen oinarriaren
poligono erregulararren aldearen berdina, eta triangeluen altura
aldeen apotema da. Kasu horretan,A = Ab + oinarriaren perimetroa bider apotema zati bi
Piramideetan, area osoa albo triangeluen area gehi oinarriarena
da. Piramidea erregularra baldin bada, alboetako triangeluak isoszeleak
izango dira, triangelu horien oinarria piramidearen oinarriaren
poligono erregulararren aldearen berdina, eta triangeluen altura
aldeen apotema da. Kasu horretan,A = Ab + oinarriaren perimetroa bider apotema zati bi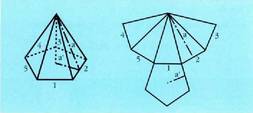 Area, oro har, oinarriaren area gehi albokoena da, eta albo area
triangeluen areen batura.
Area, oro har, oinarriaren area gehi albokoena da, eta albo area
triangeluen areen batura.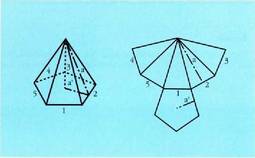 Piramideen enborren area jakin nahi baldin bada, albo irudiak
trapezioak direla gogoratu behar da, eta bi oinarri dituztela, handia
eta txikia.
Piramideen enborren area jakin nahi baldin bada, albo irudiak
trapezioak direla gogoratu behar da, eta bi oinarri dituztela, handia
eta txikia.
Irudi biribilduak
Zilindroak.
Zilindroen area albo area gehi bi oinarrien area da : aldeak sortzaile zuzen batetik abiaturik lortzen direnez gero, paralelogramoak izango dira. Zilindro zuzenen kasuan, r bada oinarriko erradioa eta h altura, albo area, lauki zuzen baten area bera izango da ; lauki zuzen horrek 2nr oinarriko zirkuluaren luzera izango du, eta h altura, hau da :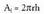 oinarrien area
oinarrien area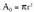 beraz area osoa
beraz area osoa
Konoak.
Kono zuzenek oinarri zirkularra dute, eta, aldea zabaldurik, zirkulu
sektore bat sortzen da, erradioa sortzailea duena. Albo area hau
da :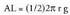 Oinarria zirkulua da :
Oinarria zirkulua da :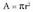 Beraz, area osoa :
Beraz, area osoa : Kono enbor baten area kalkulatzeko, kontuan izan behar da bi
oinarri direla, eta horiei albo area gehitu behar zaiela, zirkulu koroa
baten parte bat dena. Oinarriaren erradioa R baldin bada, epaiarena
r, eta g bi oinarrien arteko sortzailearen partea, albo area hau
izango da:
Kono enbor baten area kalkulatzeko, kontuan izan behar da bi
oinarri direla, eta horiei albo area gehitu behar zaiela, zirkulu koroa
baten parte bat dena. Oinarriaren erradioa R baldin bada, epaiarena
r, eta g bi oinarrien arteko sortzailearen partea, albo area hau
izango da: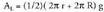 Bi epaien kenketa eginez, edota trapezio zirkulartzat hartzen baldin
bada :Area osoa hau izango da :
Bi epaien kenketa eginez, edota trapezio zirkulartzat hartzen baldin
bada :Area osoa hau izango da :
Esferak.
Esferaren gainaldea hau da : Esferaren area bolumetik atera ohi da.Ziri esferikoaren area.Ziru esferikoa A-ren angelu diedriko zentral bati baldin badagokio,
ziriaren area hiruko erregela baten bidez lortuko da :
Esferaren area bolumetik atera ohi da.Ziri esferikoaren area.Ziru esferikoa A-ren angelu diedriko zentral bati baldin badagokio,
ziriaren area hiruko erregela baten bidez lortuko da :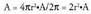 Hori, angelua radianetan adierazia badago. Angelua graduetan
badago adierazia, dagokion koefizienteaz biderkatu behar da radianetara
bihurtzeko.
Hori, angelua radianetan adierazia badago. Angelua graduetan
badago adierazia, dagokion koefizienteaz biderkatu behar da radianetara
bihurtzeko. Txapel esferikoaren area.Txapel esferikoaren altura h baldin bada, eta R esferaren erradioa,
hau izango da area :
Txapel esferikoaren area.Txapel esferikoaren altura h baldin bada, eta R esferaren erradioa,
hau izango da area :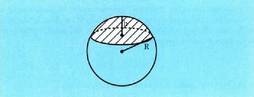 Esfera zonaren area.Bi planoen arteko altura h baldin bada, eta R esferaren erradioa,
hau izango da area :
Esfera zonaren area.Bi planoen arteko altura h baldin bada, eta R esferaren erradioa,
hau izango da area :
8. Bolumenak
Ertza luzera banakoaren berdina duen kubo bat da bolumenaren
banakoa. Hala, ertza 1 duen kubo baten bolumena :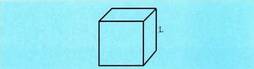 a, b eta c ertzak dituen ortoedro batean, bolumena hau izango da :
a, b eta c ertzak dituen ortoedro batean, bolumena hau izango da :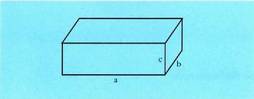 Prismetan, oinarriaren area A bada, eta altura h, hau izango da
bolumena:
Prismetan, oinarriaren area A bada, eta altura h, hau izango da
bolumena: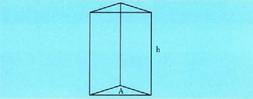 Eta horietan, poligono motaren araberakoa izaten da oinarriaren
area.Formula bera erabiltzen da zilindroetan :
Eta horietan, poligono motaren araberakoa izaten da oinarriaren
area.Formula bera erabiltzen da zilindroetan :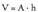 Hor, zilindroak zuzenak baldin badira,
Hor, zilindroak zuzenak baldin badira,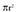 da area, oinarriaren erradioa r denean.
da area, oinarriaren erradioa r denean.
Kuboaren bikoiztea
Esmirnako Teonen arabera (K.o. 11 mendea), jainkoak adierazi omen
zuen, Delosko orakuluaren bidez, izurri bat desagertarazi nahi bazen, bere
ohorez eraiki zuten aldare bat bikoiztu behar zela. Aldarearen forma kubo
batena zen, eta ez zekiten nola bikoiztu. Delosko apaizek Platonengana
jotzea erabaki zuten, ea hark asmatzen zuen. Platonek esan zien, Teonek
kontatzen duenez, matematika ikasi behar zutela adierazi nahi ziela horrekin
Jainkoak. Beste egile baten arabera, Eratostenesen arabera (K.a 111.. endea), gauza bera gertatu zen Minos erregearen hilobiarekin, baina Platonek
bestelako erantzun bat eman omen zien Delosko apaizei. Erastotenesek
zioen Platonek bere Akademiako geometrialariei eman ziela arazoaren
berri, eta haiek soluzio bat baino gehiago aurkitu zutela, konoen edo
zilindoren ebakiduratik abiatuta, edota kurba mekanikoak erabiliz. Halaber,
Erastotenesek kontatzen du frogatu zutela problema hori a eta 2a-ren
artean bi proportzioerdi aurkitzearen baliokide dela. Alegia, bi zenbaki x
eta y aurkitzea, honelakoak: Izan ere, lehenaren kuboa hiru proportzioen biderkadurarekin berdintzen
bada,
Izan ere, lehenaren kuboa hiru proportzioen biderkadurarekin berdintzen
bada,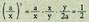 Beraz,
Beraz, Bi batezbesteko proportzionalekin, Grezian proposatzen ziren soluzio motetako bat ikus daiteke : lehen berdintasuna honen baliokidea da:
Bi batezbesteko proportzionalekin, Grezian proposatzen ziren soluzio motetako bat ikus daiteke : lehen berdintasuna honen baliokidea da: , eta bigarrena eta hirugarrena berriz, honena :
, eta bigarrena eta hirugarrena berriz, honena : . Parabola baten eta hiperbola baten ekuazioak dira horiek. Grekoek ez zuten erabiltzen funtzioen idazketa hau, baina aurkitu zuten soluzio bat : problema ebatziko zuten parabola baten eta hiberbola baten arteko kono batean beharrezko epaiak egin.Ez zuten erregela eta konpas bidezko ebazketarik aurkitu, problema
azken finean 2-ren erro kuboa aurkitzea baita, eta erro hori ezin da aurkitu
erro koadro, zatiketa eta batuketetatik abiatuz, nahiz eta hori frogatzea
zailagoa den.
. Parabola baten eta hiperbola baten ekuazioak dira horiek. Grekoek ez zuten erabiltzen funtzioen idazketa hau, baina aurkitu zuten soluzio bat : problema ebatziko zuten parabola baten eta hiberbola baten arteko kono batean beharrezko epaiak egin.Ez zuten erregela eta konpas bidezko ebazketarik aurkitu, problema
azken finean 2-ren erro kuboa aurkitzea baita, eta erro hori ezin da aurkitu
erro koadro, zatiketa eta batuketetatik abiatuz, nahiz eta hori frogatzea
zailagoa den.
Piramideak.
Piramidearen bolumena oinarriaren eta alturaren biderkaduraren
heren bat da. Izan ere, edozein piramide zatika daiteke piramide
triangeluarretan, eta era berean oinarri triangeluarreko prisma
zuzen bat hiru piramide berdinetan zatika daiteke.Izan ere, QRS oinarria eta NS altura duen prisma bat, bi poliedrotan
zatika daiteke PMS planoaren bidez. PMNS piramide triangeluarra
da. Beste poliedroa, QMS planoaz ebakiz, bi piramide
triangeluarretan zatika daiteke. Era horretan, bolumen bereko hiru
piramidetan zatikatua geratzen da. QRSM eta PMNS piramideek
jatorrizko prismaren oinarri bera eta altura bera dute, beraz, berdinak
dira. Hirugarren piramideak oinarria QRS duenaren bolumen
bera du ; izan ere, PQMR aurpegitik begiratuta, biek dute oinarri
gisa aurpegiaren erdia, eta plano horretarainoko M distantzia dute
altura. Prisma triangeluar bat hiru piramide triangeluar berdinetan
zatika daitekeenez, horietako bakoitzaren bolumena prismaren
bolumenaren heren bat izango da, alegia :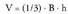 Eta hori bera erabil daiteke edozein piramidetan.
Eta hori bera erabil daiteke edozein piramidetan.
Konoak.
Kono baten bolumena ere oinarriaren eta alturaren biderkaduraren
heren bat da. Konoa zuzena bada, oinarria zirkulua izaten da,
eta bolumena hau da :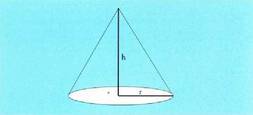 Esferak.Esferaren bolumena hau da :
Esferak.Esferaren bolumena hau da :
Cavalieriren teorema.
Area bereko oinarria eta altura bera duten bi gorputz, oinarriaren
paralelo diren planoez ebakitzen baldin badira, eta area bereko epaiak
ematen badituzte, orduan gorputz horiek bolumen bera izango dute.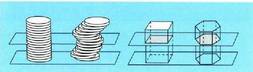 Teorema honek, irudi poliedrikoek (prismak, piramideak) eta
biribilduek (zinlindroak, konoak), bolumena aurkitzeko, zergatik
duten formula bera agertzen du ; orobat agertzen du, oinarriaren eta
alturaren area berdinarekin, prisma zuzen baten eta prisma zeihar
baten bolumena berdina izatea edo, oro har, gorputz solido zuzen
edo zeiharren bolumen berdina izatea.Esferaren bolumenaren formula agertzeko ere erabil daiteke.
Teorema honek, irudi poliedrikoek (prismak, piramideak) eta
biribilduek (zinlindroak, konoak), bolumena aurkitzeko, zergatik
duten formula bera agertzen du ; orobat agertzen du, oinarriaren eta
alturaren area berdinarekin, prisma zuzen baten eta prisma zeihar
baten bolumena berdina izatea edo, oro har, gorputz solido zuzen
edo zeiharren bolumen berdina izatea.Esferaren bolumenaren formula agertzeko ere erabil daiteke.
Horretarako, zilindro batean inskribaturiko esferaerdi bat hartzen da kontuan. Esferaren erradioa R baldin bada, zilindroaren oinarriarena ere R izango da, zilindroaren altura bezalaxe. Zilindroa plano batez ebakitzen bada, area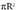 duen zirkulu bat, eta area
duen zirkulu bat, eta area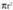 duen esfera sortuko dira, baina
duen esfera sortuko dira, baina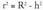 ere gertatzen da, h izanik goiko oinarriarekiko distantzia. Beraz, esferaren epaiaren area
ere gertatzen da, h izanik goiko oinarriarekiko distantzia. Beraz, esferaren epaiaren area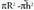 da. Hartzenbaldin bada, beste alde batetik, oinarrian R erradioa duen kono bat, eta altura ere R duena, plano batek egindako epaiak erpinetik h-ra,
da. Hartzenbaldin bada, beste alde batetik, oinarrian R erradioa duen kono bat, eta altura ere R duena, plano batek egindako epaiak erpinetik h-ra,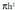 emango du, zeren ardatzak eta sortzaileak sortzen duten angelua 45°-koa baita. Hortaz, ardatzari buruz zuta den epai batean :zilindroaren area = esferaren area + konoaren area
emango du, zeren ardatzak eta sortzaileak sortzen duten angelua 45°-koa baita. Hortaz, ardatzari buruz zuta den epai batean :zilindroaren area = esferaren area + konoaren area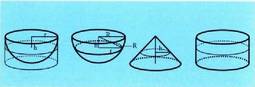 Alturak berak direnez, R hiru kasuetan, Cavalieriren teoremaz :zilindroaren bolumena = esferaerdiaren bolumena + konoaren
bolumenaBaina, zilindroaren bolumena
Alturak berak direnez, R hiru kasuetan, Cavalieriren teoremaz :zilindroaren bolumena = esferaerdiaren bolumena + konoaren
bolumenaBaina, zilindroaren bolumena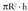 denez gero, eta
denez gero, eta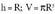 Konoaren bolumena
Konoaren bolumena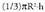 denez gero, eta
denez gero, eta Beraz, hau da esferaerdiaren bolumena :
Beraz, hau da esferaerdiaren bolumena : , eta hortik
, eta hortik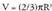 Horren ondorioz, esferaren bolumena :
Horren ondorioz, esferaren bolumena :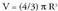 Antzeko irudien areak eta bolumenak.Antzeko bi triangelutan aldeen arteko arrazoia K baldin bada, areen arteko arrazoia
Antzeko irudien areak eta bolumenak.Antzeko bi triangelutan aldeen arteko arrazoia K baldin bada, areen arteko arrazoia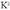 izango da.Antzeko bi gorputzen artean antzekotasun arrazoia K bada, bolumenen arteko proportzioa
izango da.Antzeko bi gorputzen artean antzekotasun arrazoia K bada, bolumenen arteko proportzioa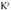 izango da.
izango da.
- Ariketak
14. Aletegi batek zilindro forma du, 3 m-ko diametroarekin eta 3 m-ko alturarekin. Kono formako teilatu batek ixten du, eta kono horrek 1,5 m du altura. Zein bolumen eduki dezake gehienera? Zein da albo gainaldea?15. Zilindro formako tunel bat eraiki da, 3 m-ko erradioa eta 150 m-ko luzera duena. Zein da harrotu den lur bolumena?16. 3 eta 4 banakoko katetuak dituen triangelu zuzen bat 4 banakoko katetu baten inguruan biratzen da. Kalkula ezazu biraketa horrek sortzen duen konoaren bolumena.17. Zein da esferaren bolumenaren eta esfera horretan zirkunskribatua dagoen zilindroaren bolumenaren arteko arrazoia?
Soluzioak
 8. Alde guztien neurria
8. Alde guztien neurria da, eta aurkako erpinak lotzen dituzten diagonalena
da, eta aurkako erpinak lotzen dituzten diagonalena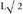 beraz, hexagono erregularra da.Horrez gainera, erpin guztiak F-tik eta D-tik
beraz, hexagono erregularra da.Horrez gainera, erpin guztiak F-tik eta D-tik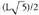 distantziara daude, beraz, plano erdibitzailean daude.9. Zortzi aurpe i eta sei erpin ditu, oktaedroa da beraz ; ertz guztien neurria
distantziara daude, beraz, plano erdibitzailean daude.9. Zortzi aurpe i eta sei erpin ditu, oktaedroa da beraz ; ertz guztien neurria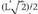 da, beraz aurpegiak triangelu aldekideak dira, eta, horretaz, oktaedro erregularra da.10. Gurpilak ez badira irristatzen
da, beraz aurpegiak triangelu aldekideak dira, eta, horretaz, oktaedro erregularra da.10. Gurpilak ez badira irristatzen egiten du itzuli bakoitzean, beraz
egiten du itzuli bakoitzean, beraz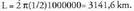 11. p baldin bada perimetroa, triangelua
11. p baldin bada perimetroa, triangelua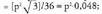 Laukia
Laukia ; eta hexagonoa
; eta hexagonoa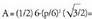 Area handiena hexagonoak du.
Area handiena hexagonoak du.