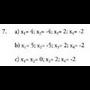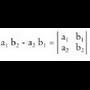Matematika»Aljebra
ALJEBRA
EKUAZIOAK ETA INEKUAZIOAK
VI. Sistemak ebaztea
VI.1. Bi ekuazio linealen sistema, ezezagun batekoa bata eta bikoa bestea.
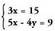 sisteman lehenengo eragiketa x bakantzea da.. = 5 ateratzen da.Ondoren, balio hori beste ekuazioan ordezkatzen da eta y bakantzen
da.
sisteman lehenengo eragiketa x bakantzea da.. = 5 ateratzen da.Ondoren, balio hori beste ekuazioan ordezkatzen da eta y bakantzen
da.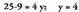
VI.2. Bi ezezaguneko bi ekuazio linealen sistema
Sistema hauek era askotara ebatz daitezke, baina egin beharreko
urratsen helburua ezezagun bakarreko ekuazio bat lortzea da.
Metodoen izena helburua lortzeko egiten den bidearen araberakoa
izaten da. Metodo horien adibideak azalduko dira orain.
VI.2.1. Erredukzio bidezko metodoa.
Metodo honen helburua hau da: ezezagun batek bi ekuazioetan
koefiziente bera izatea, baina zeinu desberdinekoa. Bi ekuazioak
batzen direnean, ezezaguna ezabatzea lortzen da.• Adibideak:1.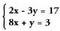 Bigarren ekuazioa 3-z biderkatzen bada, hau lortzen
da :
Bigarren ekuazioa 3-z biderkatzen bada, hau lortzen
da : Bi ekuazioak batuz gero: 26x=26, hau da, x=1.Balio hori bi ekuazioetako batean ordezkatzen da, esate baterakolehenengoan, eta hau ateratzen da :
Bi ekuazioak batuz gero: 26x=26, hau da, x=1.Balio hori bi ekuazioetako batean ordezkatzen da, esate baterakolehenengoan, eta hau ateratzen da : bakantzean, hau ateratzen da: y = -5.Sistemaren emaitza (1, -5) bakarra da, beraz, sistema bateragarria
eta mugatua da.2.
bakantzean, hau ateratzen da: y = -5.Sistemaren emaitza (1, -5) bakarra da, beraz, sistema bateragarria
eta mugatua da.2. y balioaren koefizienteak berdindu nahi badira, lehenengo ekuazioko
termino guztiak bider 2 egiten dira eta bigarren ekuazioakoak,
berriz, bider 5. Hau lortzen da :
y balioaren koefizienteak berdindu nahi badira, lehenengo ekuazioko
termino guztiak bider 2 egiten dira eta bigarren ekuazioakoak,
berriz, bider 5. Hau lortzen da :
VI.2.2. Berdinketaren metodoa.
Metodo honen bidez bi ekuazioetan ezezagun bera bakantzen da.
Behin hori egin denean, lortu diren adierazpenak berdindu eta ezezagun
bakarreko ekuazio bat lortzen da ; ondoren ezezagun hori
bakandu behar da.• Adibideak:1.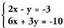 bi ekuazioetan y bakanduz gero :
bi ekuazioetan y bakanduz gero : Bi ekuzioak berdintzean :
Bi ekuzioak berdintzean : Ekuazio hori ezezagun bakarreko lehen mailako ekuazioa da.
Ekuazio hori ezezagun bakarreko lehen mailako ekuazioa da.
Aurretik azaldu bezala eginez gero, berdintza hau lortzen da : 6x + 9 = 6x + 10. Terminoak aldez aldatzean ezinezko emaitza lortzen da, izan ere baita.Emaitza horrek sistema bateraezina dela adierazten du, ez baitu
emaitzarik.2
baita.Emaitza horrek sistema bateraezina dela adierazten du, ez baitu
emaitzarik.2 x bi ekuazioetan bakantzen bada :
x bi ekuazioetan bakantzen bada : Bi adierazpenak berdintzean :
Bi adierazpenak berdintzean : Azken ekuazio hori ebaztean y = 4 lortzen da. Balio hori bigarren ekuazioan ordezkatuz gero, x-aren balioa lortzen da :
Azken ekuazio hori ebaztean y = 4 lortzen da. Balio hori bigarren ekuazioan ordezkatuz gero, x-aren balioa lortzen da : alegia. Beraz, sistemaren emaitza
alegia. Beraz, sistemaren emaitza
VI.2.3. Ordezkapen metodoa.
Metodo honetan, eragiketak ordena honetan egiten dira :• Lehenbizi, ekuazio batean ezezagun bat bakantzen da• Ondoren, lehen ekuazioan bakandutako ezezaguna bigarren
ekuazioan ordezkatzen da.• Adibideak :1.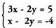 x bakandu egiten da bigarren ekuazioan : x= 2y - 4Ondoren, lehenengo ekuazioan ordezkatzen da : 3 (2 y - 4) - 2y = 5, hau da, ezezagun bakarreko ekuazioa lortzen da. Ebaztean
x bakandu egiten da bigarren ekuazioan : x= 2y - 4Ondoren, lehenengo ekuazioan ordezkatzen da : 3 (2 y - 4) - 2y = 5, hau da, ezezagun bakarreko ekuazioa lortzen da. Ebaztean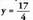 Balio hori x bakanduta dagoen ekuazioan ordezkatzen bada,
Balio hori x bakanduta dagoen ekuazioan ordezkatzen bada,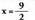 Sistemaren emaitza
Sistemaren emaitza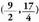 da ; sistema, beraz, bateragarria eta mugatua da.2.
da ; sistema, beraz, bateragarria eta mugatua da.2.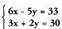 bigarren ekuazioan x bakantzen da. Eragiketa horretatik hau ateratzen
da :
bigarren ekuazioan x bakantzen da. Eragiketa horretatik hau ateratzen
da :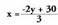 Adierazpen hori lehenengo ekuazioan ordezkatuz gero, hau lortzen
da :
Adierazpen hori lehenengo ekuazioan ordezkatuz gero, hau lortzen
da :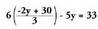
VI.2.4. Metodo grafikoa
Bedi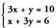 sistema.Sistemako ekuazio guztiek lerro zuzen bat adierazten dute.
sistema.Sistemako ekuazio guztiek lerro zuzen bat adierazten dute.
Ondoren koordenatu ardatz batzuetan adierazten dira.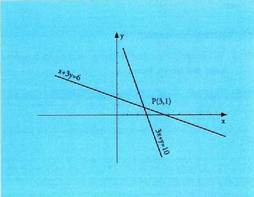 P puntu baten koordenatuak (x,y) sistemaren emaitza izan daitezen,
puntu horrek bi lerro zuzenak ukitu behar ditu. Grafikoan ikus
daiteke puntu hori (3,1) puntua dela. Puntu hori bakarra da eta
proposatutako sistemaren emaitza da.Bedi bi ezezagun dituzten bi ekuazio lineal :
P puntu baten koordenatuak (x,y) sistemaren emaitza izan daitezen,
puntu horrek bi lerro zuzenak ukitu behar ditu. Grafikoan ikus
daiteke puntu hori (3,1) puntua dela. Puntu hori bakarra da eta
proposatutako sistemaren emaitza da.Bedi bi ezezagun dituzten bi ekuazio lineal :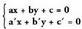 Sistema hori grafikoki ebaztean hiru kasu ager daitezke :1. Lerro zuzenak elkarren ebakitzaileak badira, puntu komun bakarra dago
Sistema hori grafikoki ebaztean hiru kasu ager daitezke :1. Lerro zuzenak elkarren ebakitzaileak badira, puntu komun bakarra dago Sistemaren emaitza bakarra puntu hori da.
Sistemaren emaitza bakarra puntu hori da. betetzen da.2. Lerro zuzenak paraleloak badira, lerroek ez dute puntu komunik eta sistemak ez du emaitzarik.
betetzen da.2. Lerro zuzenak paraleloak badira, lerroek ez dute puntu komunik eta sistemak ez du emaitzarik. betetzen da eta ez dago K zenbaki errealik
betetzen da eta ez dago K zenbaki errealik betetzen duenik.3. Lerro zuzenak bat badatoz, puntu infinituak dira ekuazioaren emaitza.
betetzen duenik.3. Lerro zuzenak bat badatoz, puntu infinituak dira ekuazioaren emaitza. betetzen da eta K zenbaki erreal bat dago hau betetzen duena :
betetzen da eta K zenbaki erreal bat dago hau betetzen duena : Hiru kasu horiei dagozkien grafikoak hauek dira :
Hiru kasu horiei dagozkien grafikoak hauek dira :
- Proposatutako ariketak
10. Ebatzi ondoko sistemak aurretik azaldu diren metodoen laguntzaz.
VI.2.5.
Badira beste hainbat metodo ekuazio linealak ebazteko : Gaussen metodoa eta Crameren metodoa edo determinatzaileen metodoa. Baina hurrengo atalean azalduko dira horiek.
VI.3. Bigarren mailako ekuazio sistemak.
Sistema bat bigarren mailakoa dela esaten da, gutxienez ekuazioetako
batek bigarren mailako termino bat badu.• Adibideak :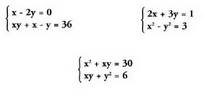 Sistema horiek ebazteko aurretik ikusitako metodoak erabil daitezke,
kasu bakoitzerako egokiena aukeratuz.Sistemak eduki dezake :
• Lehen mailako ekuazio bat
• Bigarren mailako bi ekuazio
Lehenengo kasuan urrats hauek egingo dira :1. Ezezagunetako bat ekuazio linealean bakantzen da2. Bakandu den ezezaguna ekuazio kuadratikoan
ordezkatzen da, eta ezezagun bakarreko bigarren
mailako ekuazio bat lortzen da.3. Bigarren mailako ekuazioaren erroak edo emaitzak
aurkitzen dira.4. Aurkitutako erroak edo emaitzak lehen puntuko
ekuazio linealean ordezkatzen dira.Ekuazioetako bat lehen mailakoa eta bestea bigarren mailakoa
duen sistema batek bi emaitza ditu, eta emaitza horiek zenbaitetan
irudizkoak izaten dira.• Adibidea:Ebatzi sistema hauek.1.
Sistema horiek ebazteko aurretik ikusitako metodoak erabil daitezke,
kasu bakoitzerako egokiena aukeratuz.Sistemak eduki dezake :
• Lehen mailako ekuazio bat
• Bigarren mailako bi ekuazio
Lehenengo kasuan urrats hauek egingo dira :1. Ezezagunetako bat ekuazio linealean bakantzen da2. Bakandu den ezezaguna ekuazio kuadratikoan
ordezkatzen da, eta ezezagun bakarreko bigarren
mailako ekuazio bat lortzen da.3. Bigarren mailako ekuazioaren erroak edo emaitzak
aurkitzen dira.4. Aurkitutako erroak edo emaitzak lehen puntuko
ekuazio linealean ordezkatzen dira.Ekuazioetako bat lehen mailakoa eta bestea bigarren mailakoa
duen sistema batek bi emaitza ditu, eta emaitza horiek zenbaitetan
irudizkoak izaten dira.• Adibidea:Ebatzi sistema hauek.1.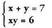 Lehenengo ekuazioko x bakanduta, x=7-y lortzen da.Ekuazio kuadratikoan ordezkatuz gero, hau lortzen da :
Lehenengo ekuazioko x bakanduta, x=7-y lortzen da.Ekuazio kuadratikoan ordezkatuz gero, hau lortzen da :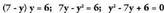 Bigarren mailako ekuazioaren emaitzak hauek dira :
Bigarren mailako ekuazioaren emaitzak hauek dira :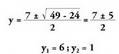 Emaitza horiek lehen puntuko ekuazio linealean ordezkatuz gero :
Emaitza horiek lehen puntuko ekuazio linealean ordezkatuz gero :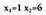 Emaitzak hauek dira : (1,6) eta (6,1)2.
Emaitzak hauek dira : (1,6) eta (6,1)2.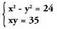 Bigarren ekuazioan x bakanduz gero :
Bigarren ekuazioan x bakanduz gero :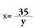 Ekuazio kuadratikoan ordezkatuz gero, laugarren mailako ekuazioa
lortzen da. Ekuazio horren ebazpena IV C.1 atalean azaltzen da.
Ekuazio kuadratikoan ordezkatuz gero, laugarren mailako ekuazioa
lortzen da. Ekuazio horren ebazpena IV C.1 atalean azaltzen da.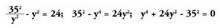 Ekuazio horretan ordezkapen hau egiten da :
Ekuazio horretan ordezkapen hau egiten da :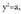 , eta bigarren mailako ekuazioa honela gelditzen da :
, eta bigarren mailako ekuazioa honela gelditzen da :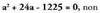
 y ezezagunaren balioak hauek dira :
y ezezagunaren balioak hauek dira :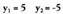 Lehen puntuko ekuazioan emaitza horiek ordezkatuz gero, hau gelditzen da:
Lehen puntuko ekuazioan emaitza horiek ordezkatuz gero, hau gelditzen da: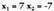 Emaitzak hauek dira : (7,5) eta (-7,-5)Sistemak bigarren mailako bi ekuazio dituenean ere ordezkapen
metodoa aplikatzen da. Zenbaitetan, sistema horiek kalkulu tresnak
erabiliaz ebazten dira. Hala ikus daiteke hurrengo adibidean :
Emaitzak hauek dira : (7,5) eta (-7,-5)Sistemak bigarren mailako bi ekuazio dituenean ere ordezkapen
metodoa aplikatzen da. Zenbaitetan, sistema horiek kalkulu tresnak
erabiliaz ebazten dira. Hala ikus daiteke hurrengo adibidean :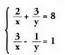 ,
,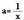 eta
eta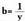 ordezkapenaren bidez bi ekuazio linealeko sistex ma lortzen da :
ordezkapenaren bidez bi ekuazio linealeko sistex ma lortzen da :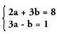 Sistema hori aurretik azaldu diren edozein metodoren bidez ebatzdaiteke, esate baterako, erredukzio bidez.a=1 eta b=2 dela ikusten da ; beraz, x=1 eta
Sistema hori aurretik azaldu diren edozein metodoren bidez ebatzdaiteke, esate baterako, erredukzio bidez.a=1 eta b=2 dela ikusten da ; beraz, x=1 eta
- Proposatutako ariketak
11. Ebatzi sistema hauek.
Bi ekuazioko problemak
Bi ekuazioko problemak ebazteko eta lehen mailako ekuazioak
ebazteko urrats berberak egin behar dira. Lehenbizi, bi
ekuazioek problemaren baldintzak betetzen dituzten konprobatu
behar da, eta ondoren, baldintzak betetzen ez dituen edo
dituzten ekuazioak baztertu.12. Ebatzi problema hauek :a)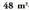 - ko gainaldea eta 28 m-ko perimetroa duen lauki zuzen baten neurriak kalkulatu.b) Hiruki angelu zuzen baten aldeak aurkitu ; kontuan hartu hipotenusa 10 m-koa eta gainaldea
- ko gainaldea eta 28 m-ko perimetroa duen lauki zuzen baten neurriak kalkulatu.b) Hiruki angelu zuzen baten aldeak aurkitu ; kontuan hartu hipotenusa 10 m-koa eta gainaldea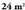
VII. inekuazioak ebaztea
Inekuazioak ebaztea hau da : ekuazioa betetzen duten ezezagunaren
balioa edo balioak aurkitzeko helburua duten eragiketen multzoa.1. 5 puntutik 1. 11 ra ikusi bezala, inekuazioak ebazteko egin behar
diren urratsak eta ekuazioak ebazteko egin behar direnak berdinberdinak
dira. Salbuespen bakarra hau da : inekuazio bat zenbaki
negatibo batez biderkatzen edo zatitzen bada, aldatu egiten da
ezberdintasunaren noranzkoa.Inekuazio bat ebazteko arauak :• Izendatzaileak, egotekotan, ezabatzen dira, termino
bakoitza bider izendatzaileen multiplo komunetako txikiena
eginez.• Parentesiak, egotekotan, banakortasun legearen bidez
ezabatzen dira.• Terminoak aldez aldatzen dira; x-eko terminoak alde
batera eta termino independenteak bestera gelditzen dira.• Termino berdinak erreduzitu egiten dira.Azkenik, ekuazioaren emaitza edo erroa aurkitzeko ezezagunaren
koefizienteaz zatitzen da termino independentea
; zatitzailea negatiboa bada, desberdintasunaren
noranzkoa aldatu behar da.• Adibideak :10. Ebatzi inekuazio hauek.a)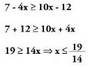 Inekuazioaren emaitza diren x-en balio guztiak
Inekuazioaren emaitza diren x-en balio guztiak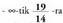 bitarteko balio guztiak dira, azkena barne. Hori horrela adierazten da:
bitarteko balio guztiak dira, azkena barne. Hori horrela adierazten da: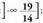 ; R lerro zuzenean honi dagokio :
; R lerro zuzenean honi dagokio :
- Proposatutako ariketak
13. Ebatzi inekuazio hauek : 14. Ebatzi inekuazio sistema hauek :
14. Ebatzi inekuazio sistema hauek :
EMAITZAK.
 2. a) Jesus=39 ; David = 21
b)N=20 ; D=25c) Pancebostik 12 km-ra suertatuko dira elkarrekin.
2. a) Jesus=39 ; David = 21
b)N=20 ; D=25c) Pancebostik 12 km-ra suertatuko dira elkarrekin.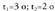 d)
d)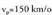 e) Miguelen adina =14 urtef) Kapitala=14.400.000 pzta.Lehenengo semea = 3.600.000 pzta.Bigarren semea=5.400.000 pzta.Hirugarren semea=4.800.000 pzta.3. a) Bi emaitza erreal eta berdin.b) Bi emaitza erreal eta desberdinc) ez dago emaitzarik. Emaitzak irudizkoak dira.
e) Miguelen adina =14 urtef) Kapitala=14.400.000 pzta.Lehenengo semea = 3.600.000 pzta.Bigarren semea=5.400.000 pzta.Hirugarren semea=4.800.000 pzta.3. a) Bi emaitza erreal eta berdin.b) Bi emaitza erreal eta desberdinc) ez dago emaitzarik. Emaitzak irudizkoak dira. Emaitza
Emaitza
Matrizeak, determinanteak, sistemak
I. Sarrera
XIX. mendearen erdi aldera agertu ziren matrizeak James Joseph Sylvester ingelesaren eskutik, nahiz eta matrizeen hasierako garapena sir William Rowan Hamilton irlandarrari eta Arthur Cayley ingelesari zor zaien. Azken honek asmatu zuen matrize idazkera, m ekuazio eta n ezazagun dituen sistema bat irudikatzeko modu laburtu gisa.Ekuazio sistemen azterketarako duten erabilgarritasunaz gainera, fisikan, kimikan, geometrian, estatistikan, ekonomian... eta abarretan ere erabiltzen dira matrizeak.Fisikan eta kimikan, aljebra ez trukakorra da mekanika kuantikoaren oinarria. Eta mekanika kuantikoa izan da, hain zuzen -beste erabilgarritasun zenbaiten artean-, atomoaren egitura korapilatsua ulertzen hasteko bidea eman duena. Werner Heisenberg, matrize kalkuluaren bitartez, eta Erwin Schroedinger, uhin mekanikaren bidez, antzeko emaitzetara iritsi ziren : alegia, elektroiak, partikula soil izan ordez, uhin izaera ere bazuela.
II. Matrizeak
II. 1. Zenbaki edo algebra ikur zerrendak
Bata bestearen segidan ipinitako zenbaki edo algebra ikur multzoei, zenbaki edo algebra ikur zerrendak deitzen zaie. Horizontalean (lerroak) edo zutika (zutabeak) egon daitezke, ondorengo adibideetan ikusten den bezala :
II. 2. Zenbaki taulak
Ohituak gaude egunkarietan taulak eta koadroak ikusten, ekonomiaren,
burtsaren, BPGaren, inflazioaren, lanik ezaren, eta abarren
bilakaerari buruzko datuak adierazi behar direnean. Esate baterako,
Europar Batasuneko edo munduko zazpi herrialde industrializatuenetako
datuak emateko.Har bedi, adibidez, txosten bat, Europar Batasunean azken bost
urteotan egindako kontratazio mugagabeak aztertzen dituena.
Emaitzak 15 lerro eta 5 zutabeko koadro batean idatz daitezke,
ondoren ikus daitekeenez :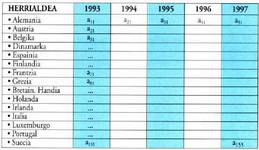 Koadro honetan, herrialde bakoitzari lerro bat dagokio eta lerro
horretan islatzen da azken bost urteotan kontratazioek izan duten
bilakaera. Zutabean, aldiz, urte horretan herrialde bakoitzak duen
egoera ikus daiteke.Oro har, letra batez eta bi azpindizez adieraz daiteke koadroko
laukitxo bakoitza. Lehen azpindizeak lerroa adierazten du, eta bigarrenak
zutabea.Horrela
Koadro honetan, herrialde bakoitzari lerro bat dagokio eta lerro
horretan islatzen da azken bost urteotan kontratazioek izan duten
bilakaera. Zutabean, aldiz, urte horretan herrialde bakoitzak duen
egoera ikus daiteke.Oro har, letra batez eta bi azpindizez adieraz daiteke koadroko
laukitxo bakoitza. Lehen azpindizeak lerroa adierazten du, eta bigarrenak
zutabea.Horrela elementu generikoa da, zeinetan i egungo Europar Batasuneko 1tamabost herrialdeak ezaugarritzen dituen lerro azpindizea den, eta j, aztertutako urtearen berri ematen duen zutabe azpindizea. Gure adibidean, zenbaki taulako elementu kopurua, labur idatzita
elementu generikoa da, zeinetan i egungo Europar Batasuneko 1tamabost herrialdeak ezaugarritzen dituen lerro azpindizea den, eta j, aztertutako urtearen berri ematen duen zutabe azpindizea. Gure adibidean, zenbaki taulako elementu kopurua, labur idatzita
II.3. Matrizeak
Baldin m eta n badira i eta jk izan ditzaketen balio handienak, m x n
elementu dituen koadro batean koka daitezke matrizeko elementuak m
lerrotan eta n zutabetan.Ilara horizontaletan (lerroak) eta zutetan (zutabeak), laukizuzen
itxuran eratutako zenbaki edo aljebra ikur multzoari
deitzen zaio matrizea. • Matrizearen dimentsioak m eta n dira. m x n biderkadurari
matrizearen dimentsioa esaten zaio.•
• Matrizearen dimentsioak m eta n dira. m x n biderkadurari
matrizearen dimentsioa esaten zaio.•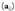 ikurrak matrize osoa adierazten du, eta
ikurrak matrize osoa adierazten du, eta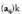 berriz, matrizelo elementu bat, edozein.• Ondorengo adibideetan ikusiko den bezala, matrizeak, ikur
berezirik gabe edota giltza, barra, kako zuzen edo kako artean
elementuak ezarrita idatz daitezke.• Baldin m = n bada, matrize karratua deitzen zaio, lerro kopurua
eta zutabe kopurua berdinak baitira. Kasu honetan, matrizea n
mailakoa dela esaten da.• Baldin
berriz, matrizelo elementu bat, edozein.• Ondorengo adibideetan ikusiko den bezala, matrizeak, ikur
berezirik gabe edota giltza, barra, kako zuzen edo kako artean
elementuak ezarrita idatz daitezke.• Baldin m = n bada, matrize karratua deitzen zaio, lerro kopurua
eta zutabe kopurua berdinak baitira. Kasu honetan, matrizea n
mailakoa dela esaten da.• Baldin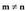 bada, matrize laukizuzena deitzen zaio.•
bada, matrize laukizuzena deitzen zaio.•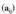 matrizearen guztizko elementu kopurua m x n da.Matrize adibideak
matrizearen guztizko elementu kopurua m x n da.Matrize adibideak
III. Matrize motak
Duten erabilgarritasunagatik eta maiztasunagatik ezagutzea komeni den zenbait matrize mota ikusiko da ondoren. Aurreko adibideek mota bakoitza aurkezteko balioko digute.1. Lerro matrizea lerro bakar bat baizik ez duena da. Esate baterako,
4. adibidea.2. Zutabe matrizea zutabe bakar bat baizik ez duena da. Esate
baterako, 2. adibidea.3. Matrize baliogabea edo zero matrizea bere elementu guztiek
zero balio dutena da. Batuketan elementu neutroa da matrize
hau.• Adibideak: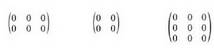 4. Matrize karratua lerro kopurua eta zutabe kopurua berdinak
dituena da. Esate baterako, 6, 7, 8 eta 9 adibideak.Matrize karratu batean lerroak eta zutabeak kontuan hartzeazgain, komeni da diagonal nagusia eta bigarren diagonalabereiztea. Lehenengoa ezkerreko goren erpinetik eskuinekomultzoa da. 6. matrizean 8,2,1 da diagonal nagusia, eta9.enean 2,1,3.Bigarren diagonala, aldiz, eskuineko goren erpinetik ezkerreko
barren erpinera doan ilaran dagoen zenbaki edo ikur multzoa
da. 6. matrizean 2,2,0 da eta 9.enean 0,1,2.5. Diagonal nagusikoak ez diren elementu guztiak baliogabeak dituen matrize karratuari matrize diagonala deitzen zaio.
4. Matrize karratua lerro kopurua eta zutabe kopurua berdinak
dituena da. Esate baterako, 6, 7, 8 eta 9 adibideak.Matrize karratu batean lerroak eta zutabeak kontuan hartzeazgain, komeni da diagonal nagusia eta bigarren diagonalabereiztea. Lehenengoa ezkerreko goren erpinetik eskuinekomultzoa da. 6. matrizean 8,2,1 da diagonal nagusia, eta9.enean 2,1,3.Bigarren diagonala, aldiz, eskuineko goren erpinetik ezkerreko
barren erpinera doan ilaran dagoen zenbaki edo ikur multzoa
da. 6. matrizean 2,2,0 da eta 9.enean 0,1,2.5. Diagonal nagusikoak ez diren elementu guztiak baliogabeak dituen matrize karratuari matrize diagonala deitzen zaio.
Adibideak: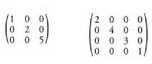 Matrize eskalarra diagonaleko elementu guztiak berdinak dituen matrize diagonala da.• Adibideak :
Matrize eskalarra diagonaleko elementu guztiak berdinak dituen matrize diagonala da.• Adibideak :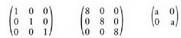 8. Goiko triangelu matrizea diagonal nagusiaz goitiko elementu
guztiak baliogabeak dituen matrize karratua da.• Adibideak:
8. Goiko triangelu matrizea diagonal nagusiaz goitiko elementu
guztiak baliogabeak dituen matrize karratua da.• Adibideak: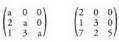 9. Beheko triangelu matrizea diagonal nagusiaz behetiko elementu
guztiak baliogabeak dituen matrize karratua da.• Adibideak:
9. Beheko triangelu matrizea diagonal nagusiaz behetiko elementu
guztiak baliogabeak dituen matrize karratua da.• Adibideak: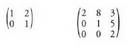 10. Matrize simetrikoa.
10. Matrize simetrikoa. ; duen matrize karratuari deitzen zaio horrela, alegia, diagonal nagusiarekiko toki simetrikoetan dauden elementuak berdinak direnean.• Adibideak:
; duen matrize karratuari deitzen zaio horrela, alegia, diagonal nagusiarekiko toki simetrikoetan dauden elementuak berdinak direnean.• Adibideak: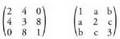 11. Matrize antisimetrikoa.
11. Matrize antisimetrikoa. ; duen matrize karratuari deitzen zaio horrela. Ondorioz, matrize antisimetriko baten diagonal nagusia zeroz osatua dago.• Adibideak :
; duen matrize karratuari deitzen zaio horrela. Ondorioz, matrize antisimetriko baten diagonal nagusia zeroz osatua dago.• Adibideak :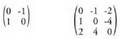 Matrize antisimetrikoei hemisimetrikoak ere deitzen zaie.12. Matrize laukizuzena lerro eta zutabe kopuruak desberdinak
dituena da.• Adibideak:
Matrize antisimetrikoei hemisimetrikoak ere deitzen zaie.12. Matrize laukizuzena lerro eta zutabe kopuruak desberdinak
dituena da.• Adibideak: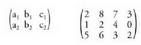 13. Matrize iraulia. A matrizea harturik, lerroak eta zutabeak tokiz aldatzean lortzen denari deitzen zaio A-ren matrize iraulia eta
13. Matrize iraulia. A matrizea harturik, lerroak eta zutabeak tokiz aldatzean lortzen denari deitzen zaio A-ren matrize iraulia eta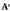 idazten da.
A-ren lehen lerroa
idazten da.
A-ren lehen lerroa -ren lehen zutabea da, A-ren bigarren lerroa
-ren lehen zutabea da, A-ren bigarren lerroa -ren bigarren zutabea, e.a.• Adibideak :
-ren bigarren zutabea, e.a.• Adibideak :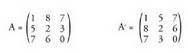 Matrize irauliaren definiziotik ondorioztatzen da A-ren diment- sioak m x n baldin badira,
Matrize irauliaren definiziotik ondorioztatzen da A-ren diment- sioak m x n baldin badira,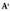 -renak n x m direla.Lerro matrizebaten matrize iraulia, beraz zutabe matrizea da, eta alderantziz.14. Aurkako matrizea. A matrizearen aurkakoa, A-ren elementu
guztiei zeinua aldatzean lortzen den -A matrizea da. Alegia, -A
matrizearen elementuak A matrizearen elementuen aurkakoak dira.• Adibideak :
-renak n x m direla.Lerro matrizebaten matrize iraulia, beraz zutabe matrizea da, eta alderantziz.14. Aurkako matrizea. A matrizearen aurkakoa, A-ren elementu
guztiei zeinua aldatzean lortzen den -A matrizea da. Alegia, -A
matrizearen elementuak A matrizearen elementuen aurkakoak dira.• Adibideak :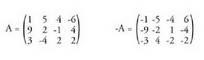 15. Azpimatrizea. m x n dimentsiotako A matrizearen
15. Azpimatrizea. m x n dimentsiotako A matrizearen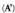 azpimatrizea, A matrizetik p lerro eta q zutabe ezabatuta lortzen dena da. Azpimatrizearen dimentsioak izango dira (m-p) x (n-q).• Adibideak :
azpimatrizea, A matrizetik p lerro eta q zutabe ezabatuta lortzen dena da. Azpimatrizearen dimentsioak izango dira (m-p) x (n-q).• Adibideak :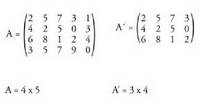
IV. Matrize berdintasunak
Kokaera berdina duten bi matrizetako elementuak berdinak badira,
matrizeak berdinak direla esaten da. Bi matrize berdinek, gainera,
dimentsioak ere hala dituzte.• Adibideak:
V. Matrize eragiketak
V 1. Matrize batuketa
Dimentsio berdinetako bi matrizeren batura, bi matrizetako indize
berbera duten elementuak ordenan batuz lortzen den dimentsio
berdineko beste matrize bat da.Bitez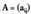 eta
eta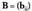 batu nahi diren matrizeak. S matrize baturak sy du elementu generikotzat, eta honela lortzen da :
batu nahi diren matrizeak. S matrize baturak sy du elementu generikotzat, eta honela lortzen da :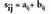 A eta B matrizeen batura horrela adierazten da : A + B• Adibideak :
A eta B matrizeen batura horrela adierazten da : A + B• Adibideak :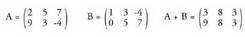 Matrizeen baturak ondorengo legeak betetzen ditu :
Matrizeen baturak ondorengo legeak betetzen ditu :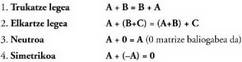
V. 2. Matrize kenketa
Ikusi da edozein dela ere A matrizea, beti dagoela -A aurkako
matrizea; horri esker honda nola defini daitekeen matrize kendura :A eta B izeneko bi matrizeren kendura A - B adierazten da eta honela definitzen da :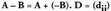 idazten badugu
idazten badugu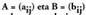 -ren arteko matrize kendura, ondorengo erlazioa gertatzen da hiru matrizeen elementu generikoen artean :
-ren arteko matrize kendura, ondorengo erlazioa gertatzen da hiru matrizeen elementu generikoen artean :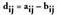
V. 3. Zenbaki erreal bat (eskalarra) eta matrize baten biderkaketa
Zenbaki erreal baten (eskalarra) eta matrize baten biderkadura, hasierako matrizearen elementu bakoitza eskalarraz biderkatzearen ondorioz lortutako beste matrize bat da. Matrize baten eta eskalar baten biderkadura honela idazten da,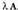 • Adibideak:
• Adibideak:
V.4. Matrize biderkaketa
V.4.a. Lerro matrize baten eta zutabe matrize baten biderkaketa.
Baldin (x,y) eta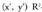 -ren bi bektore badira, biderkadura eskalarra honela definitzen da :
-ren bi bektore badira, biderkadura eskalarra honela definitzen da :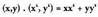 .
.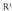 -ren bektoreen kasuan horrela definituko litzateke :
-ren bektoreen kasuan horrela definituko litzateke :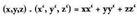 Biderkadura eskalarra definituko bada, bektore edo lerro
matrizeek elementu kopuru berbera izan behar dute.Era berean, ondorengo adierazpenaren bidez ere defini daiteke
lerro matrize baten eta zutabe matrize baten biderkadura :
Biderkadura eskalarra definituko bada, bektore edo lerro
matrizeek elementu kopuru berbera izan behar dute.Era berean, ondorengo adierazpenaren bidez ere defini daiteke
lerro matrize baten eta zutabe matrize baten biderkadura :
V.4.b. Bi matrizeren, edozeinen, biderkaketa
Matrizeen arteko biderkaduragatik da berezia eta orijinala matrize
kalkulua. Bi matrizeren arteko biderkadurak ez dauka zertan trukakorra
izanik. Beraz, beharrezkoa da matrize biderkakeean parte
hartzen duten biderkagaien ordena zehaztea.Bi matrize biderkatu ahal izateko nahitaezkoa da lehen matrizearen
zutabe kopurua eta bigarrenaren lerro kopurua berdinak izatea
. Beste modu batean esanda, A-ren dimentsioak m x n badira
eta B-renak p x q, A. B biderkaketa gauzatuko bada nahitaezkoa
da n = p izatea.
112m x n dimentsiotako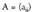 amatrizearen eta n x p dimentsiotako
amatrizearen eta n x p dimentsiotako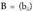 matrizearen biderkadura, m x p dimentsiotako
matrizearen biderkadura, m x p dimentsiotako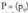 matrizea da. Matrize horretako
matrizea da. Matrize horretako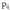 elementu bakoitza, lehen matrizearen i lerroa, bigarrenaren j zutabeaz era eskalarrean biderkatzean lortzen da.A eta B matrizeen biderkadura, A. B edo AB adierazten da.• Adibideak :
elementu bakoitza, lehen matrizearen i lerroa, bigarrenaren j zutabeaz era eskalarrean biderkatzean lortzen da.A eta B matrizeen biderkadura, A. B edo AB adierazten da.• Adibideak : • Adibidea :
• Adibidea : Matrize biderkadurak lege hauek betetzen ditu :1. Elkartze legea. A (B C) = (A B) CHurrenkera jakin batean emandako zenbait matrize biderkatu
ahal izateko, beharrezkoa da matrize bakoitzaren zutabe kopurua
eta hurrengo matrizearen lerro kopurua berdinak izatea.2. Matrize biderkadura, oro har, ez da trukakorra; hau da, AB :;'- BA• Adibideak :
Matrize biderkadurak lege hauek betetzen ditu :1. Elkartze legea. A (B C) = (A B) CHurrenkera jakin batean emandako zenbait matrize biderkatu
ahal izateko, beharrezkoa da matrize bakoitzaren zutabe kopurua
eta hurrengo matrizearen lerro kopurua berdinak izatea.2. Matrize biderkadura, oro har, ez da trukakorra; hau da, AB :;'- BA• Adibideak :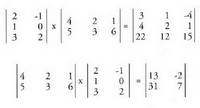 3. Bi matrize ez baliogaberen biderkadura izan daiteke matrize
baliogabea.• Adibidez:
3. Bi matrize ez baliogaberen biderkadura izan daiteke matrize
baliogabea.• Adibidez: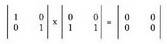 4. Elementu neutroa. Baldin A n mailako matrize karratua bada hau gertatzen da:
4. Elementu neutroa. Baldin A n mailako matrize karratua bada hau gertatzen da: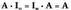 .
.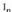 delarik n mailako unitate matrizea.5. n mailako A matrizea emanik, beti ez da existitzen
delarik n mailako unitate matrizea.5. n mailako A matrizea emanik, beti ez da existitzen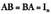 betetzen duen B matrizerik.B matrizea existitzen bada, A-ren alderantzizko matrizea dela esaten da eta
betetzen duen B matrizerik.B matrizea existitzen bada, A-ren alderantzizko matrizea dela esaten da eta
VI. Matrize baten heina. Heinaren kalkulua gaussen metodoaren bidez
Matrize baten heina, ilaraka askeak diren lerro edo zutabe kopurua da.Matrizearen heina aldarazten ez duten lerro edo zutabe aldaketa oinarrizkoak ondorengoak dira :1. Bi lerro edo bi zutabe trukatzen badira, heina ez da aldatzen.2. Matrizearen lerro bat edo zutabe bat zenbaki erreal ez baliogabe batez biderkatu edo zatitzen bada, heina ez da aldatzen.3. Matrizearen lerro bati edo zutabe bati beste bat paraleloa batzen edo kentzen bazaio, heina ez da aldatzen.Matrizearen heina ez da aldatzen ondorengoak ezabatzen badira ere :• Lerro edo zutabe baliogabeak.• Beste batzuen proportzionalak diren lerro edo zutabeak.• Beste batzuen konbinazio lineal diren lerro edo zutabeak.Aurreko eraldaketek bide ematen dute matrizearen heina Gaussen metodoaren bidez kalkulatzeko.
VII. Determinanteak
Determinante kontzeptua matrize karratuekin lotzen da soilik, ez besterekin.Bigarren mailako determinanteak, bi ezezagundun bi ekuazio linealeko sistemaren ebazpenak adierazteko sortu ziren. Era berean, hirugarren mailako determinanteek, koefizienteen eta gai askeen arabera, hiru ezezagundun hiru ekuazioko sistemaren ebazpenak ematen dituzte.
VII. 1. Bigarren mailako determinanteak
Bigarren mailako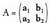 matrize karratua emanik,
matrize karratua emanik, zenbaki errealari deitzen zaio A-ren determinantea
eta det (A),
zenbaki errealari deitzen zaio A-ren determinantea
eta det (A), edo D adierazten da.
edo D adierazten da.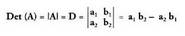 Matriz karratu baten determinantea diagonal nagusiko elementuen
biderkadurari bigarren diagonaleko elementuen
biderkadura kenduta lortzen da.• Adibideak:
Matriz karratu baten determinantea diagonal nagusiko elementuen
biderkadurari bigarren diagonaleko elementuen
biderkadura kenduta lortzen da.• Adibideak:
VII. 2. Hirugarren mailako determinanteak
Hirugarren mailako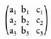 matrize karratua emanik,
matrize karratua emanik,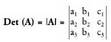 zenbaki errealari deitzen zaio A-ren
determinantea.
zenbaki errealari deitzen zaio A-ren
determinantea.
VII. 3. Hirugarren mailako determinantearen garapena
a) Sarrusen erregela erabiliz
Hirugarren mailako determinantea lortzeko Sarrusen erregelara
jo ohi da. Determinantearen eskuinetan lehen bi zutabeak idazteari
deitzen zaio horrela.Zeinu positiboko biderkadurak diagonal nagusiko elementuei eta
diagonal nagusiaren paraleloetakoei dagozkie.Zeinu negatiboko biderkadurak, aldiz, bigarren diagonaleko elementuei
eta haren paraleloetakoei dagozkie.Emaitza berbera lortzen da lehen bi zutabeak eskuinetan idatzi
ordez, lehen bi lerroak hasierako determinantearen azpian
idatzita.Azaldutakoa hobeto uler dadin bi moduetara erabiltzen da Sarrusen
erregela ondorengo adibideetan.Ariketa ebatziak.1. Kalkulatu ondorengo determinanteak : Ebazpenak:
Ebazpenak:
b) Lerro edo zutabe bateko elementuak erabiliz
Har bedi ondorengo determinantea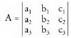 Ikusi berri den bezala, horrela garatzen da :
Ikusi berri den bezala, horrela garatzen da :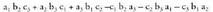 .
. eta
eta - ri ateratzen bazaizkie biderkagai komunak honela idatz daiteke :
- ri ateratzen bazaizkie biderkagai komunak honela idatz daiteke :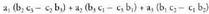 Emaitzan ageri denez lehen lerroko elementu bakoitza adjuntu izeneko batek biderkatzen du. Horrela,
Emaitzan ageri denez lehen lerroko elementu bakoitza adjuntu izeneko batek biderkatzen du. Horrela, - en adjuntua
- en adjuntua da, hain zuzen ere, A-tik
da, hain zuzen ere, A-tik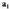 duten lerroa eta zutabea ezabatuta lortzen den determinantea
duten lerroa eta zutabea ezabatuta lortzen den determinantea Era berean
Era berean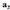 - en adjuntua, A-tik elementu hori duten lerroa eta zutabea ezabatuta lortzen da, baina aurkako zeinuarekin, toki bikoitiko lerroan aurkitzen delako.
- en adjuntua, A-tik elementu hori duten lerroa eta zutabea ezabatuta lortzen da, baina aurkako zeinuarekin, toki bikoitiko lerroan aurkitzen delako.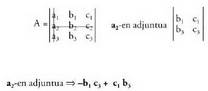 .
. dagoen lerroa eta zutabea ezabatzen badira, ondorengoa lortzen da :
dagoen lerroa eta zutabea ezabatzen badira, ondorengoa lortzen da :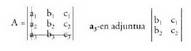 eta beraz,
eta beraz,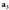 -en adjuntua
-en adjuntua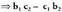 Elementu baten adjuntua, hasierako matrizetik kontuan
hartzen den elementua duten lerroa eta zutabea ezabatzean
lortzen den matrizearen determinantea da. Zeinu berdina
edo aurkakoa izango du, elementuak hartzen duen tokia
(erro bakoitian edo bikoitian dagoen arabera.Ariketa ebatziak.Garatu ondoko determinanteak lerro bateko elementuetatik
abiatuta.
Elementu baten adjuntua, hasierako matrizetik kontuan
hartzen den elementua duten lerroa eta zutabea ezabatzean
lortzen den matrizearen determinantea da. Zeinu berdina
edo aurkakoa izango du, elementuak hartzen duen tokia
(erro bakoitian edo bikoitian dagoen arabera.Ariketa ebatziak.Garatu ondoko determinanteak lerro bateko elementuetatik
abiatuta.
VIII. Determinanteen ezagurriak
Determinante bat ez da aldatzen lerroak eta zutabeak (euren artean) tokiz aldatzen badira. Beste modu batean esanda, matrize jakin baten matrize irauliaren determinantea, hasierako matrizearen determinantearen berdina da.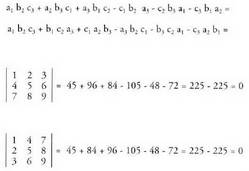 2. Determinante baten bi lerro edo bi zutabe euren artean tokiz
aldatzen badira, determinante berriak hasierako determinante-
aren balio absolutu berbera izango du, baina aurkako zeinua.
2. Determinante baten bi lerro edo bi zutabe euren artean tokiz
aldatzen badira, determinante berriak hasierako determinante-
aren balio absolutu berbera izango du, baina aurkako zeinua.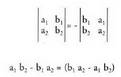 Adibideak :
Adibideak :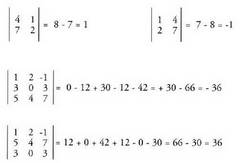 3. Lerro edo zutabe bateko elementu guztiak zenbaki batez biderkatzen badira, determinantea zenbaki berberaz biderkatua geratzen da.
3. Lerro edo zutabe bateko elementu guztiak zenbaki batez biderkatzen badira, determinantea zenbaki berberaz biderkatua geratzen da.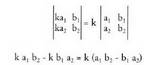 • Adibideak:
• Adibideak: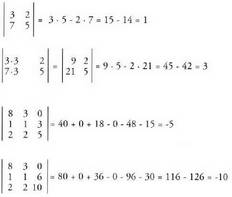 4. Lerro edo zutabe bateko elementu guztiak zeroak badira, determinantea
ere zero da:
4. Lerro edo zutabe bateko elementu guztiak zeroak badira, determinantea
ere zero da: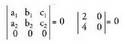 5. Determinante batek bi lerro edo bi zutabe berdinak baditu,
determinantea baliogabea da.
5. Determinante batek bi lerro edo bi zutabe berdinak baditu,
determinantea baliogabea da.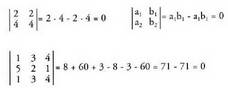 Determinante baten bi lerro edo bi zutabe proportzionalak badira, determinantea baliogabea da.
Determinante baten bi lerro edo bi zutabe proportzionalak badira, determinantea baliogabea da.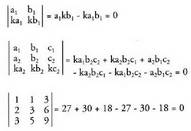 7. Determinantearen lerro edo zutabe baten ordez, beste (lerro
edo zutabe) batzuen arteko konbinazio lineala jartzen bada,
determinantea ez da aldatzen.
7. Determinantearen lerro edo zutabe baten ordez, beste (lerro
edo zutabe) batzuen arteko konbinazio lineala jartzen bada,
determinantea ez da aldatzen. 8. Determinante baten lerro edo zutabeetako bat, beste batzuen
arteko konbinazio lineala bada, determinantea baliogabea da
8. Determinante baten lerro edo zutabeetako bat, beste batzuen
arteko konbinazio lineala bada, determinantea baliogabea da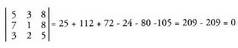 9. Baldin lerro edo zutabeetako bat batugai bat baino gehiagoz
osatua badago, lerroak edo zutabeak zenbat batugai, beste
horrenbeste determinanteren baturaren balioa izango du
determinanteak.
9. Baldin lerro edo zutabeetako bat batugai bat baino gehiagoz
osatua badago, lerroak edo zutabeak zenbat batugai, beste
horrenbeste determinanteren baturaren balioa izango du
determinanteak.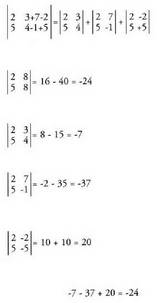 10. Lerro edo zutabe bateko elementuak bi batugaitan banatzen
badira, determinantearen balioa, hasierako determinanteak
bezainbat elementu dituzten bi determinanteren batura izango
da.
10. Lerro edo zutabe bateko elementuak bi batugaitan banatzen
badira, determinantearen balioa, hasierako determinanteak
bezainbat elementu dituzten bi determinanteren batura izango
da.
IX. Goragoko mailako determinanteak
Laugarren edo goragoko mailako matrize karratuei dagozkien
determinanteek hirugarren mailakoen determinanteen lege berberak
betetetzen dituzte, eta beraz eragiketa mota berdinak egin daitezke
determinante horiekin.Nabarmentzekoa da lerro bateko elementuetatik abiatuta egiten
den determinantearen garapenaren garrantzia, izan ere, beheragoko
mailako beste determinante batzuen bidez determinante bat adierazteko
bidea ematen baitu, harik eta hirugarren mailakoetara
heldu arte, eta hauekin, edozein mailatako determinanteak ebatzi
daitezke.Garapena egiteko orduan, lerroa tentu handiz aukeratzea komeni
da. Zero gehien edo elementu bakunenak dituena hartu behar da.
Aurreko puntuetan ikusitako legeren bat aplikatuz ere lor daiteke
lerro egokiagoa.
- Proposatutako adibideak.
X. Determinanteen aplikazioak
1. Ekuazioen ebazpena. Atal honen azken zatian aztertzen da.2. Kalkulatu zuzen bateko bi punturen arteko D distantzia.Izan bitez eta
eta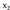 zuzen batean kokatutako bi punturen abszisak ; D ondoko formulak emango du :
zuzen batean kokatutako bi punturen abszisak ; D ondoko formulak emango du :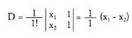 3. Triangeluaren area hiru punturen determinantearen bidez.Izan bitez
3. Triangeluaren area hiru punturen determinantearen bidez.Izan bitez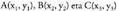 plano batean kokatutako hiru puntuak; arearen balioa ondorengo formulak emango du :
plano batean kokatutako hiru puntuak; arearen balioa ondorengo formulak emango du :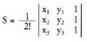 4. Tetraedroaren bolumena lau punturen determinantearen
bidez.Izan bitez
4. Tetraedroaren bolumena lau punturen determinantearen
bidez.Izan bitez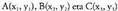 eta
eta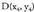 espazioan kokatutako lau puntuak ; tetraedroaren bolumena ondorengo formulak emango du :
espazioan kokatutako lau puntuak ; tetraedroaren bolumena ondorengo formulak emango du :
XI. Ekuazio linealezko sistemak ikertzea eta ebaztea
Ekuazio linealezko sistema bat ikertzea -duen ezezagun kopurua
duela- soluzioak dituen ala ez jakiteko azterketa egitea da. Soluzioren
bat aurkituko balitz, ikertzen jarraitu behar da bakarra den ala
ez jakiteko.Bateragarritasunaren edo Rouche-Frobeniusen teoremaren bitartez
egiten da lehen ikerketa hau. Ondorengo emaitzak izan ditzake
sistema batek : Bateragarritasun irizpidea edo Rouche-Frobeniusen teoremaSistema bat bateragarria da, baldin eta (eta kasu horretan bestetan ez) ezezagunen koefizienteen matrizearen heina, gai askeen zutabea gehitu zaion matrizearen heinaren berdina bada.
Bateragarritasun irizpidea edo Rouche-Frobeniusen teoremaSistema bat bateragarria da, baldin eta (eta kasu horretan bestetan ez) ezezagunen koefizienteen matrizearen heina, gai askeen zutabea gehitu zaion matrizearen heinaren berdina bada.
Sistema bateragarria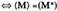
XII. Cramerren araua
XII. 1. Bi ekuazio linealezko sistemak
Izan bedi sistema bat bi ezezagundun bi ekuazioz osatua, non ezezagunen
koefizienteak eta gai askeak zenbaki errealak diren :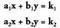 Ezezagunen koefizienteez osatutako determinanteari sistemaren
determinantea, (D), esaten zaio. Aurreko adibidean hau izango litzateke
:
Ezezagunen koefizienteez osatutako determinanteari sistemaren
determinantea, (D), esaten zaio. Aurreko adibidean hau izango litzateke
: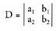 Sistemaren determinantean ezezagunei dagozkien koefizienteen
zutabearen ordez gai askeen zutabea ipintzearen ondorioz sortzen
denari ezezagunen determinantea deitzen zaio. Aurreko adibidean
x-en (Dx) determinantea hau izango da :
Sistemaren determinantean ezezagunei dagozkien koefizienteen
zutabearen ordez gai askeen zutabea ipintzearen ondorioz sortzen
denari ezezagunen determinantea deitzen zaio. Aurreko adibidean
x-en (Dx) determinantea hau izango da : eta y-rena berriz :
eta y-rena berriz : Cramerren araua horrela azal daiteke :n ezezagundun n ekuazio linealezko sistema batean,
ezezagun bakoitzaren balioa bere determinantea sistemaren
determinanteaz zatitzetik ateratzen denaren berdina
da.
Cramerren araua horrela azal daiteke :n ezezagundun n ekuazio linealezko sistema batean,
ezezagun bakoitzaren balioa bere determinantea sistemaren
determinanteaz zatitzetik ateratzen denaren berdina
da. ezezagundun
ezezagundun ekuazio linealezko sistema batean, ezezagun bakoitzaren balioa bere determinantea sistemaren determinanteaz zatitzetik ateratzen denaren berdina da.Gure sisteman hau litzateke :
ekuazio linealezko sistema batean, ezezagun bakoitzaren balioa bere determinantea sistemaren determinanteaz zatitzetik ateratzen denaren berdina da.Gure sisteman hau litzateke : Sistemaren soluzioa zenbaki erreal pare bat da
Sistemaren soluzioa zenbaki erreal pare bat da baldin eta
baldin eta eta
eta ordeztean bi ekuazioak batera betetzen badira.Aurreko formulak betetzen diren egiaztatzeko nahikoa da bi ezezagundun bi ekuaziozko sistema ebazteko behar diren ezagutzak izatea. Aurreko atalean ikusi da, sistema horiek berdinketaz, ordezketaz eta laburketaz ebatzi daitezkeela. Azken metodo hau lehengo adibideari aplikatzean, lehen ekuazioa
ordeztean bi ekuazioak batera betetzen badira.Aurreko formulak betetzen diren egiaztatzeko nahikoa da bi ezezagundun bi ekuaziozko sistema ebazteko behar diren ezagutzak izatea. Aurreko atalean ikusi da, sistema horiek berdinketaz, ordezketaz eta laburketaz ebatzi daitezkeela. Azken metodo hau lehengo adibideari aplikatzean, lehen ekuazioa biderkatzen bada eta bigarrena
biderkatzen bada eta bigarrena , batu ondoren hau ateratzen da :
, batu ondoren hau ateratzen da : x bakanduta horra zer geratuko litzatekeen :
x bakanduta horra zer geratuko litzatekeen : eta hori bat dator Cramerren arauerako azaldutakoarekin, izan ere
eta hori bat dator Cramerren arauerako azaldutakoarekin, izan ere eta
eta Era berean, lehen ekuazioa biderkatzen bada
Era berean, lehen ekuazioa biderkatzen bada eta bigarrena
eta bigarrena , batu ondoren hau ateratzen da :
, batu ondoren hau ateratzen da : y bakantzean hona zer geratzen den
y bakantzean hona zer geratzen den eta hori ere bat dator Cramerren arauerako azaldutakoarekin,
izan ere
eta hori ere bat dator Cramerren arauerako azaldutakoarekin,
izan ere eta
eta
XI. 2. Hiru ekuazio linealezko sistemak
Bi ezezagundun bi ekuaziozko sistema izan ordez, hiru ezezagundun
hiru ekuaziozkoa baldin badugu, ondorengoa adibidez, non
ezezagunen koefizienteak eta gai askeak zenbaki errealak diren :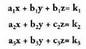 Sistemaren determinantea hau da :
Sistemaren determinantea hau da : eta ezezagunen determinanteak hauek :
eta ezezagunen determinanteak hauek : Sistemaren soluzioa zenbaki erreal hirukote bat da
Sistemaren soluzioa zenbaki erreal hirukote bat da badin eta
badin eta eta
eta ordeztean hiru ekuazioak batera betetzen badira. Horrela adieraziko litzateke hirukotea :
ordeztean hiru ekuazioak batera betetzen badira. Horrela adieraziko litzateke hirukotea : Hiru ezezagundun hiru ekuazio baino gehiagoz osatutako sistemetan
aurreko sistemetarako ikusitako metodo berberak erabiltzen dira.Gogoan hartzeko• Ekuazio linealezko sistema bati homogeneoa deitzen zaio ekuazio guztietako gai askeak baliogabeak badira.•
Hiru ezezagundun hiru ekuazio baino gehiagoz osatutako sistemetan
aurreko sistemetarako ikusitako metodo berberak erabiltzen dira.Gogoan hartzeko• Ekuazio linealezko sistema bati homogeneoa deitzen zaio ekuazio guztietako gai askeak baliogabeak badira.• ezezagundun
ezezagundun ekuaziozko sistema bati Cramerren sistema deitzen zaio baldin eta sistema homogeneo elkartuak soluzio nabaria (0,0,0) beste soluziorik onartzen ez badu.• Cramerren araua erabilgarria da n ezezagundun n ekuazio
linealezko sistemak ebazteko.• Sistemaren determinantea zero ez bada, ezezagun
bakoitzak balio bakarra du. Sistema mugatua da.• Sistemaren determinantea zero bada, bi gauza gerta
daitezke :a) Ezezagunen determinanteak zero ez izatea. Zentzurik
gabeko adierazpenetara heltzen da. Sistema bateraezina
da, ez baitu soluziorik.b) Ezezagunen determinanteak zero izatea. Sistema mugagabea
da eta soluzio infinituak ditu.Ariketa ebatziak.3. Ebatzi ondorengo sistemak Cramerren araua erabiliz
ekuaziozko sistema bati Cramerren sistema deitzen zaio baldin eta sistema homogeneo elkartuak soluzio nabaria (0,0,0) beste soluziorik onartzen ez badu.• Cramerren araua erabilgarria da n ezezagundun n ekuazio
linealezko sistemak ebazteko.• Sistemaren determinantea zero ez bada, ezezagun
bakoitzak balio bakarra du. Sistema mugatua da.• Sistemaren determinantea zero bada, bi gauza gerta
daitezke :a) Ezezagunen determinanteak zero ez izatea. Zentzurik
gabeko adierazpenetara heltzen da. Sistema bateraezina
da, ez baitu soluziorik.b) Ezezagunen determinanteak zero izatea. Sistema mugagabea
da eta soluzio infinituak ditu.Ariketa ebatziak.3. Ebatzi ondorengo sistemak Cramerren araua erabiliz
- Proposatutako ariketak
2. Ebatzi ondorengo sistema hauek Cramerren araua erabiliz
XIII. Gaussen metodoa
XIII. 1. Sistema baliokideak
Bi ekuazio sistema baliokideak dira soluzio berberak badituzte, hau da, lehen sistemaren soluzioa bigarrenaren berdina baldin bada eta alderantziz.
XIII. 2. Baliokidetasun irizpidea
1. Sistema bateko ekuazio bateko bi kideak, zero ez den zenbaki erreal batez biderkatzen edo zatitzen badira, hasierakoaren baliokide den beste sistema bat lortzen da.2. Sistema bateko ekuazio bati, sistema bereko beste ekuazio bat batzen edo kentzen bazaio, ateratzen den sistema hasierakoaren baliokidea da.3. Ekuazio linealezko sistema batean, ekuazio bat beste batzuen konbinazio lineala bada, ekuazio hori ezaba daiteke, eta geratzen den sistema hasierakoaren baliokidea da.
XIII. 3. Laburketa metodoa edo Gaussen metodoa.
Ondoko sistema hauek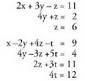 triangeluarrak direla esaten da.Lehenengoa ebazteko nahikoa da hirugarren ekuazioko z, bigarren
ekuazioko y, eta lehen ekuazioko x aurkitzea. Hau da soluzioa :
(9,-1,6)Bigarrena ebazteko laugarren ekuazioan t aurkitu behar da, z
hirugarrenean, y bigarren ekuazioan eta x lehenengoan. Hona soluzioa
: (4,-2,1,3)Laburketa metodoa -Gaussen metodoa, triangelutzearena
edo ur-jauzi metodoa ere deitzen zaio- ekuazio
linealezko sistema bat balio bereko sistema triangeluar
bihurtzea da, dagozkion eragiketak egin ondoren.Ariketa ebatziak.4. Ebatzi ondoko sistema hauek Gaussen metodoa erabiliz.
triangeluarrak direla esaten da.Lehenengoa ebazteko nahikoa da hirugarren ekuazioko z, bigarren
ekuazioko y, eta lehen ekuazioko x aurkitzea. Hau da soluzioa :
(9,-1,6)Bigarrena ebazteko laugarren ekuazioan t aurkitu behar da, z
hirugarrenean, y bigarren ekuazioan eta x lehenengoan. Hona soluzioa
: (4,-2,1,3)Laburketa metodoa -Gaussen metodoa, triangelutzearena
edo ur-jauzi metodoa ere deitzen zaio- ekuazio
linealezko sistema bat balio bereko sistema triangeluar
bihurtzea da, dagozkion eragiketak egin ondoren.Ariketa ebatziak.4. Ebatzi ondoko sistema hauek Gaussen metodoa erabiliz.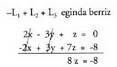 ematen du eta ondorengo sistema triangeluarra ateratzen da
ematen du eta ondorengo sistema triangeluarra ateratzen da -L, + LZ + L 3 eginda berriz ematen du eta ondorengo sistema triangeluarra ateratzen da [*]
non
-L, + LZ + L 3 eginda berriz ematen du eta ondorengo sistema triangeluarra ateratzen da [*]
non
- Proposatutako ariketak
3. Ebatzi ondoko sistema hauek Gaussen metodoa erabiliz.
Soluzioak
- Proposatutako ariketak
2. Ebatzi ondoko sistema hauek Cramerren arauaren
bidez. 3. Ebatzi ondoko sistema hauek Gaussen metodoa erabiliz
.
3. Ebatzi ondoko sistema hauek Gaussen metodoa erabiliz
.